一种煤矿事故分析与预测的新方法

陈学辉++李正贵

摘要：煤矿开采属于特种作业，人的不安全行为和物的不安全状态都可能引发事故的发生，容易造成重大人身伤害和财产损失。事故的分析和预测是安全的重要保证，针对事故树顶上事件的发生概率对系统安全评价的重要性，首先介绍了集对分析的基本理论，以及集对分析理论与事故树分析的结合求解顶上事件发生概率的模型；接着举例加以说明，并分析计算结果；最后总结了运用集对分析方法在对顶上事件发生概率进行判定的优越性。同以往的求解的方法相比，集对分析理论是从同一性、差异性和对立性三个方面对基本事件发生概率进行预测，这样更加的符合煤矿系统工程实际。

Abstract： Coal Mining is a special operation， the unsafe behavior or material insecurity is likely to cause accidents， leading to significant personal injury and property damage. Accident Analysis and forecasting is an important guarantee of security， for the importance of the fault tree top event's occurrence probability for systematic safety assessment， first， the theory of set pair analysis and the solution model that the theory of set pair analysis combines with fault tree analysis at the aspect of top event's occurrence probability are introduced. Next， some examples are taken to explain the method and the calculation result is analyzed. Last， the advantages of using set pair analysis to judge the top event's occurrence probability are summarized. Comparing with previous solutions， set pair analysis theory predicts the basic events' occurrence probability from 3 aspects： identity， difference， and opposition， which is more consistent with coal mine system engineering reality.

关键词：煤矿开采；集对分析；顶上事件；事故树

Key words： coal mining；set pair analysis；top event；fault tree

中图分类号：X928 文献标识码：A 文章编号：1006-4311（2017）21-0178-03

0 引言

我国是一个煤矿大国，煤矿开采过程中事故的发生屡见不鲜，每一次都是血淋淋的教训，分析和预防事故的发生已成为煤矿实际生产的重中之重。对事故的分析和预防的方法较多，定性分析、定量分析、定性与定量结合分析是目前最常用的三种方法。但上述三种方法，不同程度上存在主观性强、简单化、模糊化，因此普遍适应性较差[1，2]。本文针对目前常用事故分析方法的局限性，引入集对分析理论，将该理论与事故树分析相结合，提出一种新的分析方法。

1 集对分析的基本理论

1.1 集对分析的概念

集对（Set pair，SP），是指不确定性系统中的有一定联系的两个集合组成的对子，一般表示为H（A，B）。例如：上下、刚柔、虚实、大小、胜负、高低、胖瘦、好坏等，以及作用力与反作用力、化合与分解、正电与负电、太阳与地球、物质与能源，还有系统与环境、历史与未来、教师与学生、领导与群众、安全与不安全等等，无一例外地是成对地存在。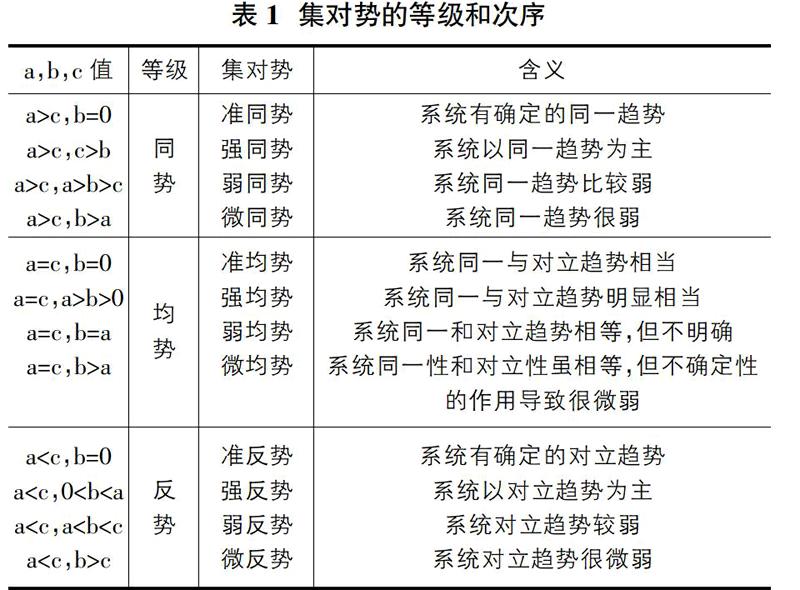

集对分析[3]（Set pair analysis，SPA），是指对不确定性系统中的两个有关联的集合构造集對，对集对的某些特性做同一性、差异性、对立性分析，建立集对的同、异、反联系度的分析方法。可见，SPA的基础是集对，关键是联系度的构建和计算。

1.2 联系度与联系数

1.2.1 联系度与联系数的概念

事物是普遍联系的，各类事物通常在某些特定属性方面存在一定关系。三分原理，就是把这些关系的程度用三个明显的特征来描述。集对分析方法，其核心思想是先对不确定性系统中的有关联的两个集合构造集对，再对集对做某些特定属性做同一性、差异性、对立性分析，然后用联系度描述集对的同异反关系。设有联系的集合X和Y，X和Y都有n项表示其特性，因此有X=（x1，x2，x3，…，xn），Y=（y1，y2，y3，…，yn）。表述H（X，Y）关系的联系度的概念为[4]

式中：S表示同一性的个数；

F表示差异性的个数；

P表示对立性的个数；

S+F+P=n；

I表示不确定系数，在（-1，1）区间视不同情况取值，有时仅起差异标记作用；

J表示对立系数，且J=-1，有时仅起对立标记作用；

μX～Y表示集对H（X，Y）的联系度。

令a=S/n，b=F/n，c=P/n，由式（1）可得

μX～Y=a+bI+cJ （2）

式中：a表示同一度；

b表示差异度；

c表示对立度；

a+b+c=1。

上式（2）中，a表示集合X和Y关于某种属性具有相同性质的程度；b表示集合X和Y关于某种属性具有既不相同也不相反的性质程度；c表示集合X和Y关于某种属性具有相反性质的程度。如果a越趋近于1时，表示这两个集合的关系越趋近于同一；b越趋近于1时，表示这两个集合的关系越趋近于差异；c越趋近于1时，表示这两个集合的关系越趋近于对立。

当I和J取合理值时，μX～Y变成一个数值，称为这个数值为联系数，记为μ'X～Y。根据联系度的定义有：

-1≤μ'X～Y≤1。

1.2.2 联系度与联系数的意义

联系度（μX～Y），通过a、b和c定量表征了不确定性系统中集合X和Y多层次上的关系，描述的系统是一个不确定性的系统；并能清晰地显示关系的整体性和局部结构，直观定量地揭示复杂关系中的三种或多种秉性；它表征了综合不确定性，同时也是是动态的。

联系数是表征集对H（X，Y）关系程度的一个综合定量指标。集合X和Y趋向于相同，则联系数大；相反，集合X和Y趋向于相反，则联系数小。当μ'X～Y接近于1、0、-1时，分别表示这两个集合在某特定属性方面越倾向于同一、对立和差异。

1.2.3 集对势

联系度μX～Y=a+bi+cj中的c≠0时，同一度a与对立度c的比值a/c为集对势。根据集对势，可以得出系统安全状态和发展趋势。

2 联系度的基本算法和应用法则

2.1 联系度的和积运算法则[5-7]

2.1.1 联系度的加法法则

设有μ1=a1+b1i+c1j，μ2=a2+b2i+c2j，两个联系度的加法有如下法则

μ1+μ2=a1+a2+（b1+b2）i+（c1+c2）j

=2[（a1+a2）/2+（b1+b2）i/2+（c1+c2）j/2]（3）

2.1.2 联系度的乘法法则

根据联系度乘法运算法则，ij=i，i2=i，j2=1，因此两个联系度相乘如下：

μ1μ2=（a1+b1i+c1j）（a2+b2i+c2j）

=a1a2+a1b2i+a1c2j+a2b1i+b1b2i2+c2b1ij+a2c1j+c1b2ij+c1c2j2

=（a1a2+c1c2）+a1b2i+a2b1i+c2b1ij+c1b2ij+b1b2i2+（a1c2+a2c1）j

=（a1a2+c1c2）+（a1b2+a2b1+c2b1+c1b2+b1b2）i+（a1c2+a2c1）j（4）

在这里仅仅是列举了两个联系度的和积算法，根据联系度的算法规则，可以推广到n个聯系度的和积形式。

2.2 集对分析与事故树的融合

对于在事故树方面运用集对分析的基本原理，下面举例说明集对分析在事故树方面的运用[8，9]。

假设对某一事故树顶上事件发生概率进行计算时，各基本事件为x1，x2，x3，…，xn，存在下面两种情况：

3 集对分析法在事故树分析中的运用

如图1所示为某次煤矿事故事故树图的简化，各基本事件的联系度系数如表2给出。运用联系度的方法计算顶上事件的联系度（μX～Y）和联系数（μ'X～Y）[10]。

①根据事故树图可得如下：

T=G3+G4

=X1G1+X2G2

=X1（X3+X4）+X2（X5+X6）

=X1X3+X1X4+X2X5+X2X6

从上式可以得出，事故树有四个最小割集，分别为{X1，X3}，{X1，X4}，{X2，X5}，{X2，X6}。

②运用上面提到的事故树顶上事件联系度的计算公式可得如下：

μT=μ1（μ3+μ4）+μ2（μ5+μ6）

=2（0.1+0.5i+0.4j）（0.1+0.75i+0.15j）

+2（0.1+0.4i+0.5j）（0.1+0.45i+0.45j）

=2（0.07+0.875i+0.055j）+2（0.235+0.67i+0.095j）

=4（0.1525+0.7725i+0.075j）

在式μT=4（0.1525+0.7725i+0.075j）中，式中系数4表示事故树中最小割集的个数为4个，对μT分析，只需考虑μT″=0.1525+0.7725i+0.075j。由于联系数-1≤μ'X～Y≤1，将μT″分为三个区间“危险”[-1，-0.333]，“一般安全”[-0.333， 0.333] ，“安全”[0.333，1]。j作为对立面恒取j=-1。

对式μT″=0.1525+0.7725i+0.075j进行分析：

①当 i=-1时，μT″=-0.695，系统安全等级为“危险”；当i=0时，μT″=0.145，系统安全等级为“一般安全”；当i=1时，μT″=0.85，系统安全等级为“安全”。因此μT″的取值范围为[-0.695，0.85]。μT″的下线为-0.695处于危险当中，必须引起重视，应查找薄弱环节，及时整改加强安全管理水平，提高系统安全等级。

②根据集对势对μT″进行分析可知，b（0.7725）最大，系统处于“一般安全”中。根据表1，b>a>c，属于微同势，整体处于“临界安全”状态，但是系统同一势很弱，也即“安全”趋势很弱。因此，应当查找危险源，规避风险。由于b较大，系统处于“临界安全”的权重较大，而系统在运行的过程总是处于“危险”、“一般安全”和“安全”三个等级中循环，因此由“一般安全”状态转向“危险”状态概率也增大。在定期的安全检查中，对于系统处于“一般安全”等级中，应当引起足够的重视，防止其向“危险”状态转移。

4 结论

①本文引用同一性、差异性、对立性三个方面概率替代单一顶上事件发生概率，并针对系统安全状态运用集对分析的基本原理和方法进行分析，改变了传统方法对事故分析的单一性和局限性。

②为了最大程度地降低顶上事件发生概率，本文一方面考虑了在最小割集或径集中出现频率较高的事件；另一方面运用集对分析理论，并进行举例论证，提出了降低“差异性事件”发生概率的方法。

③根据集对分析的基本原理，可对单一差异性进行替換，即将bi替换为b1i1+b2i2+b3i3+…+bnin。以此进行计算和分析，提高了差异性的维度，可以得到更加精准的结果。

参考文献：

[1]徐志胜.安全系统工程[M].北京：机械工业出版社，2007.

[2]崔国章，张景林.安全系统工程[M].北京：煤炭工业出版社， 2002.

[3]赵克勤.集对分析及其初步运用[M].杭州：浙江科技出版社，2000.

[4]王文圣，李跃清，金菊良等.水文水资源集对分析[M].北京：科学出版社，2010.

[5]赵克勤，米红.非传统安全与集对分析[M].北京：知识产权出版社，2010.

[6]赵克勤.集对分析的不确定性系统理论在AI中的应用[J].智能系统学报，2006，1（2）：16-25.

[7]刘秀梅，赵克勤.基于集对分析联系数的信息不完全直觉模糊多属性决策[J].数学的实践与认识，2010，40（1）：67-77.

[8]黄大荣，黄丽芬.基于集对分析联系数故障树的BA系统可靠性分析[J].计算机应用研究，2010，27（1）：111-113.

[9]廖文来，何金平.基于集对分析的大坝安全综合评价方法研究[J].人民长江，2006，37（6）：57-58，61.

[10]郑欣，许开立，周家红.基于集对分析的尾矿库安全评价研究[J].安全与环境学报，2008，8（1）：160-162.