基于四叉树算法优化检索效率的三维建模技术

卢鹏飞，黄轲，龙奎，魏文刚，潘声勇，杨其菠，江君

(1.重庆市地质环境监测总站，重庆 401120；2.武汉中地数码科技有限公司，武汉 430074；3.重庆地质矿产研究院，重庆 400042)

基于四叉树算法优化检索效率的三维建模技术

卢鹏飞1，黄轲2，龙奎1，魏文刚2，潘声勇2，杨其菠2，江君3

(1.重庆市地质环境监测总站，重庆 401120；2.武汉中地数码科技有限公司，武汉 430074；3.重庆地质矿产研究院，重庆 400042)

三维地质建模是研究如何利用GIS软件将三维空间地质实体真实地再现，实现地质体的三维可视化和相关空间分析，为地质研究和矿产资源勘查提供技术支撑。本文在综合前人研究成果的基础上，对目前常用的基于MapGIS的三维地质建模方法进行了总结，并提出了一种利用四叉树算法优化检索效率的三维建模技术，对于解决城市地质、工程地质、环境地质、三维地质填图中的三维建模问题具有重要意义。

三维地质建模；MapGIS；四叉树；检索效率

1 引言

三维地质建模(Three-dimensional Geological Modeling)，即三维GIS技术在地学上的应用[1]，以各种原始数据(包括钻孔、剖面、地震数据、等深图、地质图、地形图、物探数据、化探数据、工程勘察数据、水文监测数据等)为基础，建立能够反映地质构造形态、构造关系及地质体内部属性变化规律的数字化模型[2]。相对于传统的二维地质数据表示方法，三维模型能够完整准确地表达复杂地质现象的边界条件及地质体内含的各种地质构造，直观地再现地质单元的空间展布及相互关系，最大限度地提高地质分析的直观性和准确性[3]。如今在资源和环境的双重压力下，地质找矿，地质灾害监测预警的研究更加深入，传统的二维地质图主要专注于地表和浅部的地质环境，已经无法满足地球科学发展和资源环境的需求，人们逐渐开始将眼光转向地球深部，对三维地质模型的构建提出了要求。

目前，国内对于三维地质建模的研究主要体现在两个方面：①三维地质建模的基础原理和技术研究，包括三维数据模型、建模方法等；②三维地质模型构建的具体方法和应用研究[4-6]。在利用城市多专题的地质数据进行三维地质模型构建时，针对不同类型、不同特性的地质数据，选择不同的三维建模方法[7]。本文综合前人的研究成果[8-12]，重点总结三维结构模型的构建技术。

2 常用三维地质建模方法对比

2.1 多源数据耦合层状地质体自动建模

对于工程地质、水文地质等简单层状地质体，可采用“钻孔-剖面/等值线-地层实体”构模的整体建模思路(图1)。采用所有地层界面共用的网格模板来构建各个地层面，根据建模范围和精度(网格间距)要求生成地形网格。在此基础上，从基础数据库中提取钻孔点位和分层信息叠加等值线数据生成地层面强约束点，从剖面中提取有关地层边界线信息，基于地形网格应用这两类数据进行插值计算构造各地层面模型，最后根据地层之间的叠覆关系等地质信息生成地层实体模型。同时，对于地表模型可添加地形约束，构建出真实地形地貌单元的地质模型。对建立完的地质模型，可以不断的添加各种约束数据，指定约束数据的影响范围，对地质模型进行反复的重构更新，从而更精确的去表现真实的地质形态。

图1 多源数据耦合层状地质体自动建模

2.2 基于地层分区图的地质图快速建模

基于地层分区图的地质图快速建模方法采用“自顶向下”的思想，逐层建立每一个层面的顶层地质面(图2)。最顶层面看作是一个完整的地质面，以这个完整的地质面为基础，根据每一个层面的地质分区图，向下逐层建立地质面。按由粗到精的建模思想进行建模，分别按系、统、组、段和岩性等进行划分，依次建立一级、二级、三级和四级等地质模型。使用钻孔、剖面、等高线、平面地质图、地层分区图等多源数据作为三维建模的数据源，首先进行建模数据的一致性处理，数据处理工作贯穿整个建模流程。

整体建模过程为：首先，建立地表地质分区图约束下的地质子面；其次，通过剥离当前需要处理的地层，将后续地质表面建模转化为最上层的地质子面建模；然后，通过标准地层层序，依次构建出所有地质体的地质子面模型；最后，通过拓扑处理，构建出地层实体结构模型。

2.3 基于剖面的复杂地质体半自动交互建模

根据地质数据特点，可应用剖面交互式建模方法构建基岩地质三维地质结构模型、第四系地质三维地质结构模型。

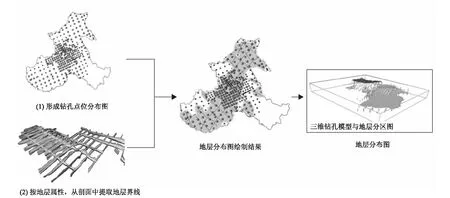
图2 分区图建模流程

由于地质专业不同，勘探线的布置方法不同。实际建模中往往会遇到空间位置近似交叉和近似平行的两种剖面情况，分为基于近似平行剖面的轮廓线拼接和基于单元格的“分区-拼接”两种交互建模方法(图3)。根据建模范围内的实际地质情况，基岩地质模型和第四纪地质模型一般可采用这种建模方法，这种建模方法将复杂模型进行分割，便于观察和操作，也便于分工合作完成大数据量复杂模型构建。

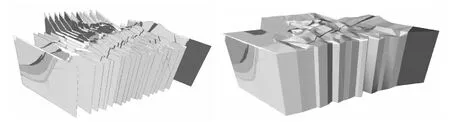
图3 基于轮廓线拼接的剖面建模

2.4 基于“分区-拼接”的半自动建模

“分区-拼接”建模方法采用“分治”的方法将复杂模型进行分割，便于观察和操作，也便于分工合作完成大数据量复杂模型构建(图4)。其建模基本思路为：利用建模区域内多条交叉剖面将空间分割成多个单元格，用户建模的最小单元就是一个个单元格，所做工作就是利用单个单元格内一系列闭合轮廓线建立起曲面片，进而确定该单元格内所有地质体的空间几何形态，形成一个单元格地质块，最后将每个单元格的地质块进行合并形成完整的地质体模型。对于非交叉剖面或边界处无法自然封闭的单元格，可以通过手动添加辅助线的方式进行封闭，之后按照封闭单元格相同方式建模。除剖面数据外，在单元格内的空白区域，如果有钻孔、等值线数据能够揭示地质体或地质构造信息，也可将这些信息在构面过程中加以利用，提高模型精度。

3 利用四叉树算法改进三维建模技术

3.1 四叉树定义

四叉树(也被称为Q树、Q-Tree)是在二维图片中定位像素的唯一适合的算法。因为二维空间中，平面像素可以重复的被分为四部分，树的深度由图片、计算机内存和图形的复杂度决定。在二维平面中，可以使用两条正交的直线将一个矩形的区域划分为4个部分，这4个部分正好与四叉树的4个子节点对应，如图5所示。

四叉树(quad-tree)每个节点最多有4个子树，可以用来在数据库中放置和定位文件(称作记录或键)。这一算法通过不停的把要查找的记录分成4部分来进行匹配查找直到仅剩下一条记录为止。

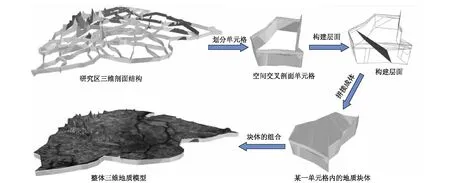
图4 半自动复杂地质体快速交互式建模技术

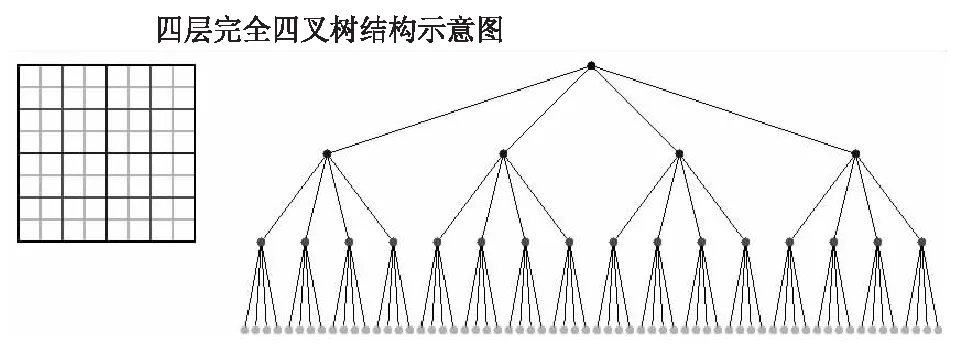
图5 四叉树划分二维区域实例

在树中，记录被存储在叶子的位置上。这一名字的由来是因为记录被存储在端点上，他们上面再没有节点了。分支被称作节点。数的顺序是每节点的分支(也称孩子)数。在四叉树中，每个节点通常有4个孩子，因此顺序是4。四叉树的叶子数也是4。为达到想要的记录所进行的查找操作次数成为树的深度。

对于地理空间信息，四叉树定义是：它的每个节点下至多可以有4个子节点，通常把一部分二维空间细分为4个象限或区域并把该区域里的相关信息存入到四叉树节点中。这个区域可以是正方形、矩形或是任意形状。

3.2 四叉树的常规检索过程和构建过程

对二维空间进行划分之后，可以实现对指定点或者指定矩形范围内存在哪些数据进行快速检索。通常，进行四叉树检索的流程如下：

(1) 从四叉树的根节点开始，判断该节点是否与指定的范围相交。

(2) 如果不相交，则在指定的范围内不存在数据。

(3) 如果相交，再对节点的4个子节点进行同样的处理，直到找到所有没有子节点的节点。

(4) 第3)步中找到的所有节点所包含的数据，即为最后的检索结果。

从检索的过程可以看到，检索的思路类似于二分查找，不过此处使用的是更复杂的四分法。在不停的四分的过程中，不断的将检索的范围缩小。相对于在整个数据集合中进行遍历查找，效率当然更高。理论上可以达到O(n)的时间复杂度。而四叉树的实现过程，又非常简单。

所以四叉树很适合进行二维的数据处理，例如二维的空间索引、二维图像数据压缩，还包括图像处理、二维快速碰撞检测、存储稀疏数据等。图6是将二维点位数据进行四叉树构建的示例。

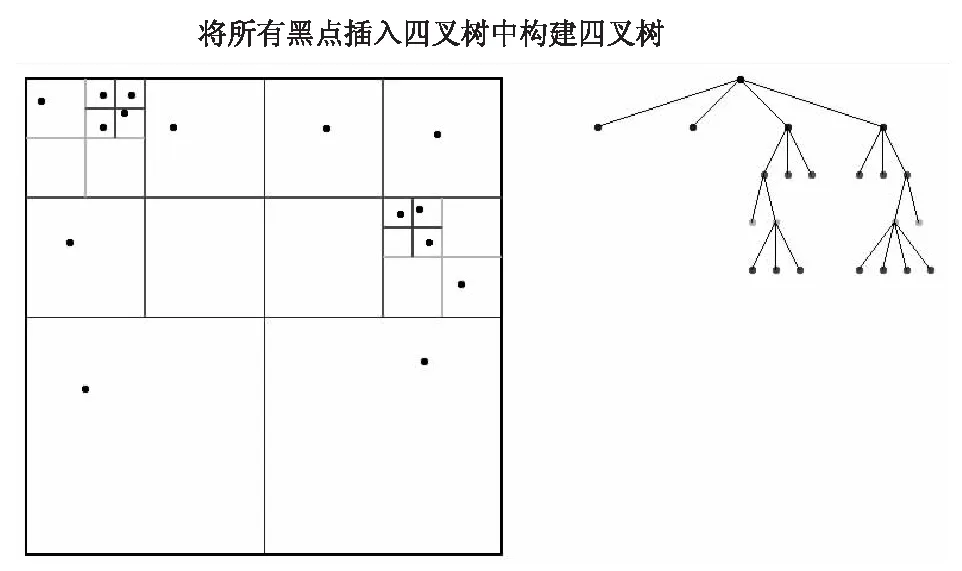
图6 二维点位数据的四叉树构建

(1) 首先将所有数据使用蓝色的线两分为四，为树中的一级节点。

(2) 现在下方的两个矩形区域，每一个矩形内已经只有一个数据，可以不进行下一级的细分了。上方的两个矩形区域，还需要进一步细分。

(3) 使用红色的线，将上方的两个矩形区域分别重复步骤(1)进行两分操作，得到树的二级节点。此时又有一部分矩形区域已经满足不需进一步细分的条件。

(4) 将所有不满足停止细分条件的矩形进行递归细分处理，最后可以得到一个完整的四叉树索引。

3.3 四叉树的优化方案

通过大量的数据测试与分析，我们发现，四叉树的检索效率会随着树的深度的增加而严重下降。为了解决这个问题，我们对四叉树进行了改进，在四叉树中加入了两个阈值。

(1) 四叉树的最大深度h可以设置。

(2) 四叉树的每一个节点包含的数据个数n可以设置。

(3) 进行四叉树节点细分时，先判断该节点的深度是否小于h。如果不小于h，则不进行进一步细分；如果小于h，则进行下一步判断。

(4) 判断节点所包含的数据，是否大于n。如果不大于n，也不进行细分；如果大于n，则进行一次细分。

通过加入树的最大深度h和节点的数据个数n两个控制项，我们简化了四叉树的结构，通过不断的调节h和n两参数，达到检索效率的最优。

另外，为了使得四叉树可以较好的扩展，以适应各种复杂的应用场景，我们采用模板的方式实现四叉树。由于C++不支持浮点数类型(float,double)，我们使用了数据精度的倒数来确定四叉树的检索精度。

3.4 四叉树的C++实现过程

简单介绍了四叉树的原理以及一些简单的改进方案之后，我们来看看四叉树的一个C++实现版本。主要定义了4个类：CRect、CQTreeNode、CQTreeDataBase、CQTreeBase。

(1) CRect用于抽象二维空间范围。

(2) CQTreeNode用于抽象四叉树节点。

(3) CQTreeDataBase用于抽象二维的数据。

(4) CQTreeBase用于抽象四叉树。

这4个类相互结合，最终完成四叉树的完整功能实现。下面是4个类的声明和关键接口说明：

(1) CRect

用于抽象二维空间范围，还实现了四叉树检索中的空间范围相交判断算法以及空间四分算法，声明如下：

// Effect: -矩形坐标范围

// TCoor: -坐标的数据类型，如int、float、double等数值型

// precision 坐标计算的精度

// Brief : -

template

class CRect

{

public:

CRect();

explicit CRect(TCoor xmin, TCoor ymin, TCoor xmax, TCoor ymax);

virtual ～CRect();

//

}

①自动拆分范围

// Effect: -获取左上角拆分范围

// Rtn: -

// Brief : -

CRect GetLTRect();

// Effect: -获取右上角拆分范围

// Rtn: -

// Brief : -

CRect GetRTRect();

// Effect: -获取左下角拆分范围

// Rtn: -

// Brief : -

CRect GetLBRect();

// Effect: -获取右下角拆分范围

// Rtn: -

// Brief : -

CRect GetRBRect();

②范围相交判断

// Effect: -判断指定的点位是否在举行范围内

// In : -

// In : -

// Rtn : -

// Brief : -

bool Inter(TCoor x, TCoor y);

// Effect: -判断指定的矩形范围是否和当前范围相交

// In : -

// Rtn : -

// Brief : -

bool Inter(const CRect& rhs);

(2) CQTreeNode

用于抽象四叉树节点，实现对二维空间范围以及数据的管理，声明如下：

// Effect: -四叉树节点

// TCoor : -坐标的数据类型，如int、float、double等数值型

// TData : -节点携带的数据的类型

// Brief : -

template

class CQTreeNode

{

public:

// 矩形范围

typedef CRect CRect;

explicit CQTreeNode(CRect rect, ushort depth);

explicit CQTreeNode(CRect rect, ushort depth, vector datas);

～CQTreeNode();

//

}

关键接口与成员如下：

// Effect: -判断指定的点位是否在节点内部

// In : -

// In : -

// Brief : -

bool IsCoorInNode(TCoor x, TCoor y) const;

// 节点的数据范围，所有子节点的范围的并集

CRect _rect;

// 四个子节点

CQTreeNode* _lt; // 左上

CQTreeNode* _rt; // 右上

CQTreeNode* _lb; // 左下

CQTreeNode* _rb; // 右下

vector _datas; // 节点数据

ushort _depth; // 节点的深度

(3) CQTreeDataBase

这是一个抽象类，用于抽象二维的数据。要求所有的数据类，必须从此类派生。声明如下：

// Effect: -四叉树数据基类

// TCoor : -坐标的数据类型，如int、float、double等数值型

// Brief : -定义四叉树数据必须实现的接口

template

class CQTreeDataBase

{

public:

explicit CQTreeDataBase() { }

virtual ～CQTreeDataBase() { }

// 获取X坐标

virtual TCoor X() const = 0;

// 获取Y坐标

virtual TCoor Y() const = 0;

};

(4) CQTreeBase

用于抽象四叉树，是四叉树数据结构的完整定义。该类使用模板类实现，同时可以支持派生子类，可以很好的进行扩展，以适应不同的业务逻辑。声明如下：

// Effect: -四叉树基类

// TCoor : -坐标的类型，例如int,float,double等

// TData : -数据的类型，必须实现CQTreeDataBase所指定的接口

// int precision : -坐标比较的精度的倒数，如E-6,则传入E6

// Brief : - int precision使用精度的倒数的原因是浮点型不能作为模板参数

template

class CQTreeBase

{

public:

// 矩形范围

typedef CRect CRect;

// 四叉树节点

typedef CQTreeNode CQTreeNode;

// Effect: -构造一个四叉树对象

// In : -整体的数据范围，在该范围之外的数据，无法加入到四叉树中

// In : -四叉树的最大深度，深度达到最大值的节点，将停止拆分

// In : -每一个四叉树节点可以携带的最大数据点位个数，

// 当节点携带的数据点位个数超过该值时，节点将自动拆分

// Brief : -

CQTreeBase(const CRect& rect, ushort maxDepth, ulong maxDataNum);

virtual ～CQTreeBase();

// ……

};

关键接口：

①矩形检索，实现在四叉树中的矩形范围检索

// Effect: - 矩形检索

// In : - 坐标范围

// In : -

// In : -

// In : -

// Out : - 检索结果

// Rtn : - 矩形内部或者矩形边上的点

// Brief : - 数据量很大的时候，不推荐调用该函数获取结果

bool Search(TCoor xmin, TCoor ymin, TCoor xmax, TCoor ymax, vector& hitedDatas) const;

// Effect: - 矩形检索

// In : - 坐标范围

// In : -

// In : -

// In : -

// Out: - 检索结果

// Rtn: - 与矩形碰撞的节点

// Brief : -

bool Search(TCoor xmin, TCoor ymin, TCoor xmax, TCoor ymax, vector& hitedNode) const;

②点检索，实现四叉树的点位检索

// Effect: - 点检索

// In : -

// In : -

// Rtn : - 该点所在的节点

// Brief : -

CQTreeNode* Search(TCoor x, TCoor y) const;

// Effect: - 点检索

// In : -

// In : -

// Rtn : - 该点所在的节点的第一个数据

// Brief : -

TData* SearchData(TCoor x, TCoor y) const;

③添加数据，实现添加一个数据到四叉树中

// Effect: - 添加一个数据点到树中

// In : - 数据

// Rtn : -

// Brief : -

bool AddData(TData* data);

④拆分节点，实现四叉树的节点拆分功能

// Effect: - 拆分指定的节点

// In : -

// Rtn : -

// Brief : -

virtual bool SpiltNode(CQTreeNode* node);

⑤关键数据成员

protected:

CQTreeNode* _root; // 根节点

ushort _maxDepth; // 树的最大深度

ulong_maxDataNum;

// 树节点的最大数据数量

3.5 四叉树在三维建模算法中的主要应用

四叉树主要用于分割二维空间，构建快速索引。前文已经介绍了四叉树的基本原理，同时给出了一个典型的C++实现。下面将结合实际应用，说明四叉树在重庆建模中的一些实际应用。

(1) 缓存地表等高线

构建模型的第一步，就是构建模型的地表。构建地表的数据，主要是地表等高线。在重庆建模时，使用的是一幅高精度的地表等高线。这幅等高线，在构建每一个出露地层的地表面的时候，都要使用其作为高程数据源。

为了避免频繁地打开这幅高精度的等高线而导致系统效率低下的问题，我们必须将其缓存在内存中。当然，常规的一维线性数组，是这完成不了这项工作的。

四叉树的链式存储，恰好解决了这个问题。由于没有采用连续内存存储数据，理论上可以使用电脑的所有可用内存；同时，四叉树又提供了快速的数据检索支持。所以立即决定使用四叉树作为数据缓存的方式。在解决了内存不足的问题的同时，也为后续的地表构建提供了快速数据检索支持。

(2) 计算地表边界高程

在有了四叉树缓存的地表等高线数据之后，我们使用地层的地表边界，从四叉中检索出地层范围内的高程点，进行三角化操作，可以得到完整的地表面，如图7所示。

但是这个操作有一个前提，我们的地层地表边界的z值必须确定。而事实上的边界数据是没有高程的。所以需要通过地表等高线，对边界的z值进行插值计算，来获取边界的z值，这样才能正确构建地表模型。

而地表等高线的数据量庞大，插值过程非常慢，甚至可能由于内存不足而无法计算出边界的z值。

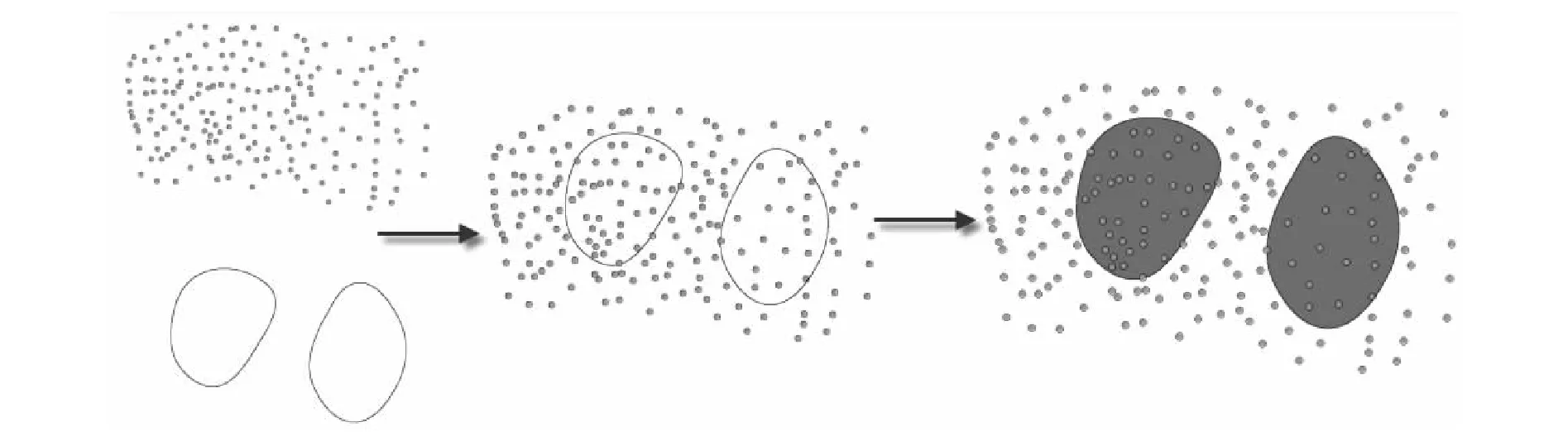
图7 利用边界范围和高程点插值构建地表模型

此时，有两种优化方案来解决这个问题：

①使用地层边界内的高程点对地层边界z值进行插值(图8)。

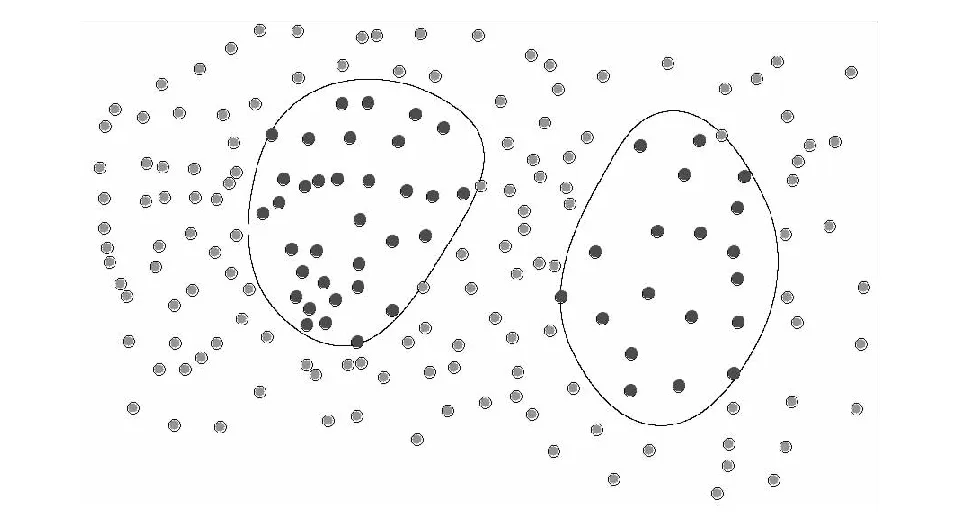
图8 利用地层边界内的高程点插值

②使用地层边界一定范围的缓冲范围内的高程点对地层边界z值进行插值(图9)。

图9 利用地层边界缓冲范围内的高程点插值

对比之下，显然第2种方案更优：

①进行调和插值的数据量，通常会更小，插值计算速度更快。

②对边界z值插值的准确性，理论上会更高。因为获取了边界内外的高程点进行了计算。

但是地表边界的缓冲范围，通常是一个环形的区。然而四叉树并不支持环形复杂区检索，所以必须对算法思路进行调整。采用对边界进行分段处理的方法，将边界上的每一条线段进行缓冲处理，得到每一条线段的缓冲范围，并使用每一个范围在四叉树中进行检索，最后将检索得到的高程数据合并为一个集合，对模型边界进行高程插值计算，可以得到地表边界的高程值(图10)。

可以看到，四叉树在计算地层边界的高程值时，在效率和准确性方面，起到了关键性的作用。解决了大数据量下的高程插值导致的内存不足和精度不够的问题。

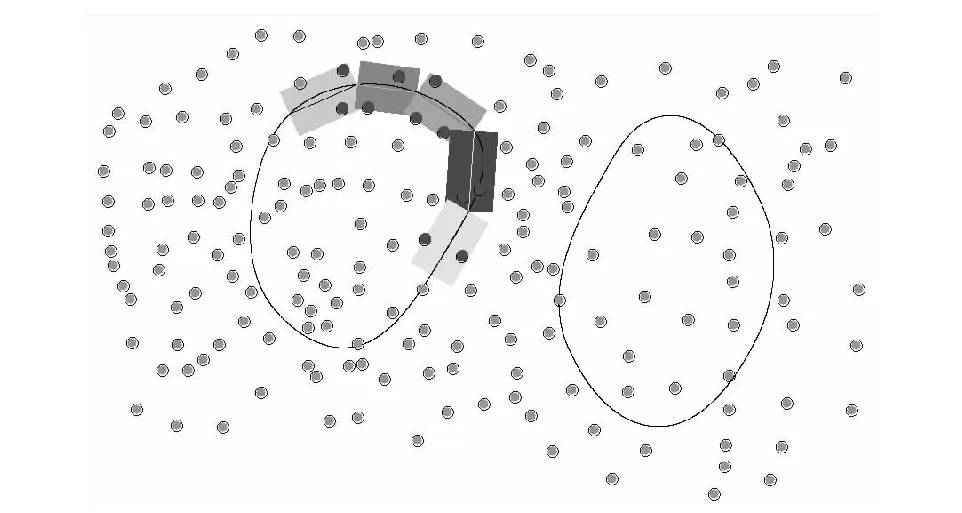
图10 边界分段处理法插值

(3) 计算地层边缘形态

在构建模型的边缘部分的时候，有两种情况：

①边缘地层厚度为0，地层在边缘处尖灭(图11)，此时需要处理地层的尖灭问题。

图11 地层尖灭于一点

②边缘地层有一定的厚度，此时需要在地层边缘处构建一个竖直面来封闭地层模型。

在建模的整个流程中，地层边缘形态是比较难处理的。在构建模型这两种边缘模型的过程中，也使用到了四叉树作为很重要的一种工具。

地层边缘处理过程主要如下：

①处理地层尖灭

通过一定的技术手段，我们保证了模型在边缘处的顶面和底面的边界点的x、y坐标一致。同时模型的顶面已经构建完成，顶面边缘处的x、y、z值以及完整的坐标序列已经完成计算。此处的任务，就是计算地层底面边缘的z值。

对问题进行进一步分析可知，找到底面边界上的每一个点A对应的顶面边界上的点B，并将B的z值作为A的z值，即可完成底面边界z值计算的任务(图12)。

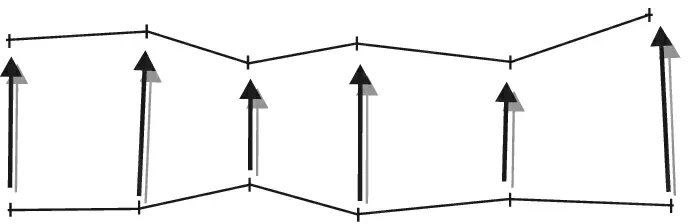
图12 底面边界点z值使用顶面边界z值

当问题转化为一个二维点数据检索的问题，那么很自然的就联想到使用四叉树来处理。这是四叉树的一个典型的应用。使用模型的顶面边界点，构建一个四叉树索引，再到四叉树索引中检索出底面边界的每一个点的z即可(四叉树的构建参考3.4节)。

②构建竖直面封闭模型

本身已经有一种自动三角化的算法，可以实现侧面的自动构建。但原算法在处理侧面时存在一定的缺陷，没有将x、y值相同的点进行连接(图13)。

图13 一种不好的可能的三角化连接方式

这本身并不是一个非常影响建模效果的问题，但是在存在一定角度的情况下，这种三角化很影响建模效果，导致模型的侧面看起来很不自然。

当然，此处和“处理地层尖灭”实际上是一个问题，需要从顶面的边界中，检索出底面边界的每一个点对应的顶面边界点，然后在三角化时，需要将顶面边界和底面边界相对的点连接在一起(图14)。检索的过程，和处理“处理地层尖灭”是相同的，此处不做详细介绍。三角化的具体算法，也不在此处进行讨论。

图14 优化后的三角化效果

4 结语

三维地质建模在现如今的城市地质、三维地质填图研究项目中具有非常重要的作用。本文首先总结了几种典型的基于MapGIS的三维地质建模方法，然后提出了一种利用四叉树算法改进三维建模技术的方法。通过四叉树算法优化和改进插值点检索效率能较大的提高三维建模插值速度，极大地节省了建模时间。但是由于四叉树是主要针对二维空间地理位置的一种算法，应用到三维空间中存在一定的局限性。针对三维空间有另一种类似的优化算法，即八叉树算法。如何利用八叉树算法对三维地质建模技术进行优化是后续改进的一个大方向。

[1] 朱良峰,吴信才,刘修国,等.基于钻孔数据的三维地层模型的构建[J].地理与地理信息科学,2004,20(3):26-30.

[2] Simon W Houlding. 3D geoscientific modeling computer technique for geological characterization[M].Springer Verlag,1994.

[3] 陈学习,吴立新,车德福,等.基于钻孔数据的含断层地质体三维建模方法[J].煤田地质与勘探,2005,33(5):5-8.

[4] 明镜.三维地质建模技术研究[J].地理与地理信息科学,2011,27(4):14-18.

[5] 潘懋,方裕,屈红刚.三维地质建模若干基本问题探讨[J].地理与地理信息科学,2007,23(3):1-5.

[6] 焦养泉,朱培民,雷新荣,等.地学空间信息可视化技术应用研究[J].地质科技情报,2005,24(1):1-6.

[7] 潘懋,方裕,屈红刚.三维地质建模若干基本问题探讨[J].地理与地理信息科学,2007,23(3):1-5.

[8] 张像源,王新春,孟利山.基于DSI算法和多源数据耦合的天津市中心城区工程地质三维模型的建立[J].工程勘察,2013,41(5):76-80.

[9] 刘扬,宫阿都,李京.基于数据分层分块的海量三维地形四叉树简化模型[J].测绘学报,2010,39(4):410-415.

[10]花卫华,廖艳云,刘修国,等.基于子面模板库的第四纪三维地质模型快速构建[J].地球科学-中国地质大学学报,2013,38(5):1128-1134.

[11]明镜.三维地质建模技术[J].地理与地理信息科学,2011,27(4):14-18.

[12]安聪荣,刘展,王心众.基于层面结构的地质块体拓扑关系的自动构建[J].测绘学报,2012,41(1):147-151.

THREE-DIMENSIONAL MODELING TECHNOLOGY WITH OPTIMIZATION OF RETRIEVAL EFFICIENCY BASED ON QUATREE ALGORITHM

LU Peng-fei1，HUANG Ke2，LONG Kui1,WEI Wen-gang2，PAN Sheng-yong2，YANG Qi-bo2，JIANG Jun3

(1.Chongqing Institute of Geological Environment Monitoring, Chongqing 401120,China; 2.WUHAN ZONDY CYBER-TECH CO., LTD, Wuhan 430074,China; 3.Chongqing Institute of Geology and Mineral Resources, Chongqing 400042,China)

Three-dimensional geological modeling is to study how to obtain the realistically reproduction of the three-dimensional space and geological entity by GIS. It is able to realize three-dimensional visualization and correlation space analysis, providing technical support for geological research and mineral exploration. On the basis of previous research findings, several current three-dimensional geological modeling methods based on MapGIS are summarized. In addition, an improved three-dimensional modeling technology with optimization of retrieval efficiency taking advantage of quatree algorithm is proposed. It has significant meaning for solving problems related to urban geology, engineering geology, environmental geology and three-dimensional geological mapping.

three-dimensional geological modeling； MapGIS； quatree； retrieval efficiency

1006-4362(2017)02-0084-09

2017-02-17 改回日期： 2017-04-12

中国地质调查局，重庆都市经济圈城市地质调查(1212011220032)

P628

A

卢鹏飞(1986- )，男，汉族，工程师，本科，主要从事区域地质调查、城市地质三维建模等方面的研究。 E-mail：402443685@qq.com