大兴安岭松岭大扬气林场落叶松生长规律研究
先文娟,杨子健,梁丹,刘璐
(辽宁省林业调查规划院,辽宁 沈阳 110122)
大兴安岭松岭大扬气林场落叶松生长规律研究
先文娟,杨子健,梁丹,刘璐
(辽宁省林业调查规划院,辽宁 沈阳 110122)
树木生长量的大小及生长速率,一方面受树木本身遗传因素的影响,另一方面也受所处环境条件的制约。以大扬气林场的兴安落叶松为研究对象,基于其37株标准木的树干解析、生长数据,利用线性模型、对数模型、多项式模型、指数模型研究不同测树因子(胸径、树高等)之间的关系,分析模拟其生长规律。结果表明:在研究区域内,多项式模型模拟所得到的相关系数相对较高,因此可以利用此模型来预估此区域落叶松的生长规律。
兴安落叶松;生长规律;模型;树高;胸径;材积;带皮直径;去皮直径
Abstract The growth and growth rate of trees are not only influenced by the genetic factors ,but also by the trees and the environmental conditions. TakingLarixgmeliniiin Dayangqi Forest Farm as research objects,based on the tree stem analysis and growth data of 37 standard woods, the relationship among different tree sizes (DBH, tree height) were studied by using linear model, logarithm model, polynomial model and exponential model;the growth laws were simulated. Result shows that the model can be used to predict the growth ofLarixgmeliniiin this area,tre correlation coefficient obtained by polynomial model simulation is relatively high.
Key wordsLarixgmelinii; growth law; model;tree height;DBH; timber volume; diameter outside bark(DOB); diameter inside bark(DIB)
1 研究区域概况
兴安落叶松属落叶乔木,松科落叶松属,天然分布广泛,主要集中于我国内蒙古林区、东北高山上,是东北地区三大用材林树种之一,也是大兴安岭的主要组成树种。
研究区位于大兴安岭松岭区大扬气镇松岭林业局大扬气林场,大扬气林场于1970年正式成立,位于松岭区(局)中部,北与劲松镇相接,南同绿水林场、翠峰林场毗连,东邻古源林场,西与阿里河林业局接壤。地理坐标50°50′ N,123°50′ E。海拔300~700 m。
大扬气林场所处区域属寒温带大陆性季风气候,冬季严寒期长,夏季炎热期短。年均温度-2.8 ℃,最高温度为37 ℃,最低温度为-43 ℃,年均降雨量490.1 mm。年均蒸发量1 153 mm,年相对湿度63.5%。降雪期为9月至翌年6月,最大积雪量为36 cm,封冻期为145~165 d。植物生长期100 d左右。纵观全镇西高东低,属低山小丘陵,坡度变化不大。境内东西走向的两大主山脉,又派生了南北走向的52条支脉。河流24条,总长187.7 km。
2 研究内容与方法
分别测定37株落叶松的胸径、树高、冠幅等因子,并且在每株树胸高处,树高的20%、40%、60%、80%处各截取5 cm厚圆盘1个。从圆盘的南向自髓心向外各取30°楔形木块,在每个楔形木块角度平分处画一条直线,根据这条直线把楔形木块划分成均匀相等的8份,并测量出每一部分的年轮数和宽度。随后,进行最小二乘法计算,拟合得到生长规律模型。
2.1 生长规律模型
树木生长量的大小及生长速率,一方面受树木本身遗传因素的影响,另一方面受外界环境条件的制约。在这双重影响下,经过树木内部生理生化的复杂过程,表现在树高、直径、材积及形状等因子的生长变化过程。我们对一定区域的树木进行测量时,会测量其树高、胸径以及年轮数,通过这几个因子对模型进行检验总结,得到了以下几种模型公式:
(1)线性模型公式:Y=aX+b
(1)
(2)对数模型公式:Y=alnX+b;
(2)
(3)二次多项式模型公式:Y=aX2+bX+c
(3)
(4)指数模型公式:Y=aebX;
(4)
其中:X-样木的年轮数
Y-样木的胸径或树高、材积等
2.2 统计评价方法
用于评价样地以及预测模型的方法有相关系数法、残差平方和法、均方差法等,本文采用相关系数法。公式为:
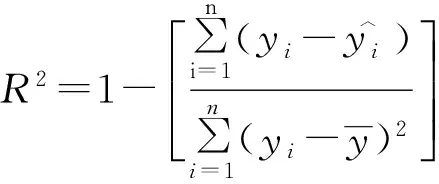
(5)
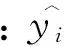
3 研究结果与分析
3.1 落叶松树龄和树高模型建立
以兴安落叶松的年轮数为横坐标,树高为纵坐标,生成散点图,根据散点图添加趋势线。通过对兴安落叶松散点图的分布及趋势的分析,树龄与树高关系曲线分别建立线性、二次多项式曲线、对数曲线、指数曲线等几种模型方程。在此基础上建立相对应的拟合模型,模型模拟结果见图1-图4,模型相关参数见表1。

图1 线性模型

图2 对数模型

图3 二次多项式模型
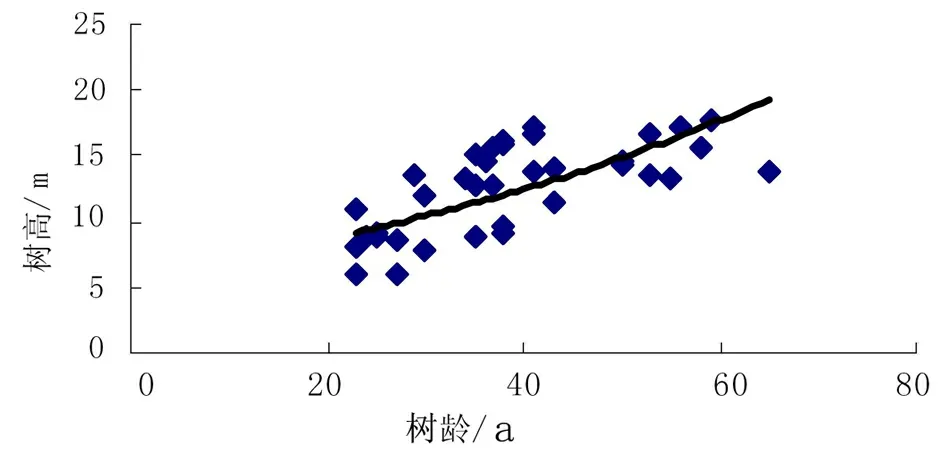
图4 指数模型
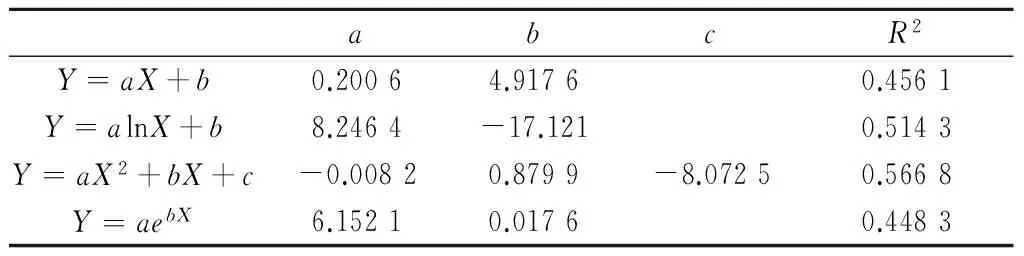
表1 各模型参数估计值及拟合统计量
计算相关系数,根据相关系数大小确定要选取的模型的精度。因此比较各模型的相关系数,可以选择出该树种的最优模型。
由表1中的相关系数可以看出,几个模型计算得到的相关系数并没有特别大的差异,基本稳定在0.5附近。如果利用相关系数作为评价指标来对各模型的最优程度进行排序,其优劣程度为:多项式模型优于对数模型,对数模型优于线性模型,线性模型优于指数模型。由于二次多项式模型计算得到的相关系数最高。因此,我们认为在模拟落叶松生长规律的模型当中,多项式模型能够更好地描述树木的年龄与树高的生长关系。
3.2 落叶松树龄和胸径模型建立
以兴安落叶松的年轮数为横坐标,胸径为纵坐标,生成散点图,通过散点图建立预估计模型。通过对散点图的分布及趋势的观察,选择年轮数-密度线性模型、多项式曲线、对数曲线、多项式曲线、指数曲线这几种模型方程。随后,采用对比和观察的方法,进行数据拟合,便会得到相对应的模型估计方程,模拟结果如图5~图8所示,拟合参数见表2。
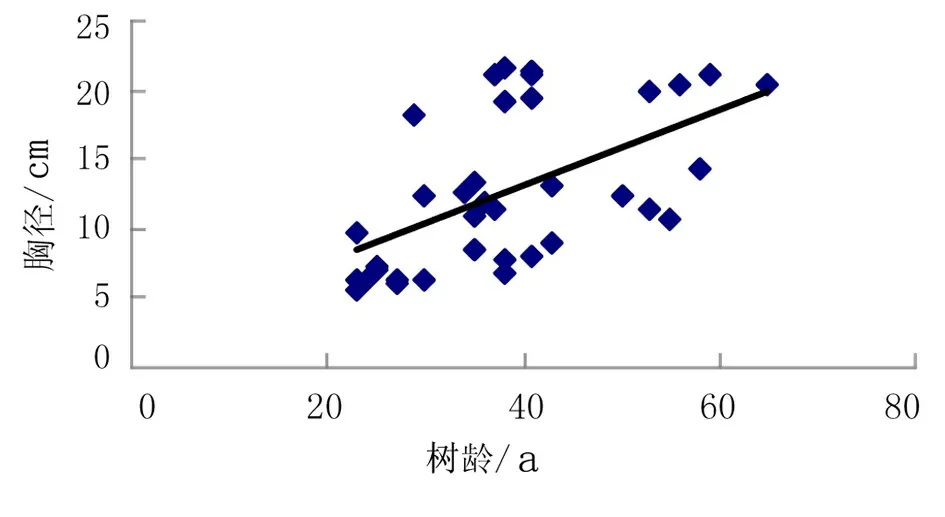
图5 线性模型

图6 对数模型

图7 二次多项式模型
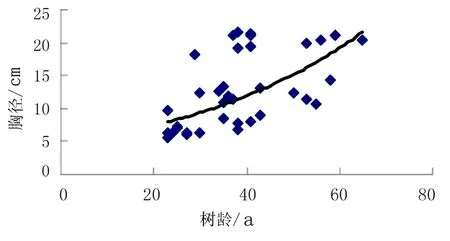
图8 指数模型

abcR2Y=aX+b0.27422.10770.3175Y=alnX+b11.023-27.1190.3424Y=aX2+bX+c-0.00650.8133-8.20130.3434Y=aebX4.57660.02390.3659
从拟合效果上看,在对落叶松进行年龄-胸径的曲线模型拟合所建立的四种模型中,指数和多项式模型明显优于线性模型和对数模型。这二者中,指数模型(图6)拟合效果更佳,所以用指数模型来拟合落叶松的年轮数-胸径曲线关系能够得到很实际的应用效果。而利用线性模型进行模拟得到的相关系数比较低,因此,在实际应用中,可以不考虑利用它来进行落叶松的年轮数-胸径的线性模型模拟。
3.3 落叶松树龄和材积模型建立
以落叶松的树龄为横坐标,材积为纵坐标,生成散点图,利用散点图建立预估计模型。通过对散点图的趋势及分布的观察,选择年轮数-密度曲线类似二次多项式曲线、线性模型、对数曲线、三次多项式曲线这几种模型方程。采用对比和观察的方法,进行数据拟合,得到4个相对应的模型估计方程,模拟结果如图9~图12所示,拟合参数见表3。
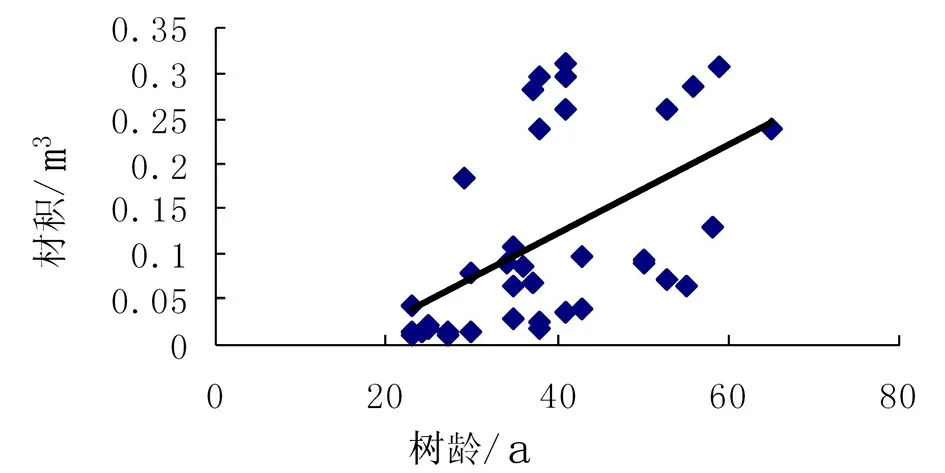
图9 线性模型

图10 对数模型

图11 二次多项式模型

图12 三次多项式模型

abcdR2Y=aX+b0.0049-0.07230.2723Y=alnX+b0.1943-0.58620.2902Y=aX2+bX+c-0.00010.0154-0.27930.4152Y=aX3+X2+cX+d1E-05x3-0.00130.0625-0.84830.4336
分别用直线、对数、二次多项式、三次多项式模型方程来对落叶松的年轮数-材积进行曲线拟合,从图9~图12可以观察出:图9和图10的拟合效果不是特别好,图11、图12的拟合效果优于图9和图10,即应用二次多项式、三次多项式模型拟合效果都好于对数模型和线性模型。因此,在实际应用中,可以考虑用二次或三次多项式模型来对落叶松年轮数和材积关系进行描述。
综合表3和图9~图12可以看出,无论用哪种模型,落叶松的相关系数都很低。在这种情况下应检查数据录入是否正确、是否存在其他错误,分析得到这种情况的原因,并采取一些措施减小误差,例如增加样本数量,或研究其他相关因素。修正数据之后,重新得到散点图,进行数据拟合和分析。最后,在所有模型中选择出相关性最高的模型。
3.4 利用落叶松各年份圆盘带皮直径建立模型
类似地以落叶松的圆盘年龄为横坐标,各年的带皮直径值为纵坐标,生成散点图,通过散点图建立预估计模型。通过对散点图的分布及趋势的观察,选择线性模型、对数模型、多项式模型、指数模型这四种模型方程。采用对比和观察的方法进行数据拟合,便会得到相对应的模型估计方程,模拟结果如图13~图16所示,拟合参数见表4。

图13 线性模型

图14 对数模型
落叶松圆盘年龄和各年带皮直径曲线可能接近线性、二次多项式、对数、指数等四种模型方程,结合表4可以看出,多项式得到的相关系数最高,如果把相关系数作为评价指标,对几种模型的优劣程度进行排序,其结果为:二次多项式模型优于线性模型,线性模型优于对数模型,对数模型优于指数模型。因此,关于落叶松的生长模型建立,采用二次多项式模型来进行拟合能够更好地描述圆盘年龄和各年带皮直径的生长关系。

图15 多项式模型

图16 指数模型

abcR2Y=aX+b2.85736.26930.9504Y=aln(X)+b31.614-33.0740.9336Y=aX2+bX+c-0.01143.16424.63390.9509Y=aebX14.310.07630.8560
由表4还可以看出,采用不同的模型进行拟合时得到的相关性差异较大,例如指数模型和多项式模型的相关系数相差了大约0.1。因此,我们可以推测,在实际应用中要多进行实践和对比,选择最合适的模型,才可以达到最理想的效果。
3.5 利用落叶松各年份去皮直径建立模型
类似地,以落叶松的各圆盘年龄数为横坐标,各年份的去皮直径为纵坐标,生成散点图,依据散点图建立预估计模型。通过对散点图的趋势和分布的分析观察研究,选择年轮数-去皮直径线性模型、多项式模型、对数模型、指数模型这四种模型方程。采用对比和观察的方法,进行数据拟合,得到相对应的四种模型估计方程,模拟结果如图17~图20所示,拟合参数见表5。
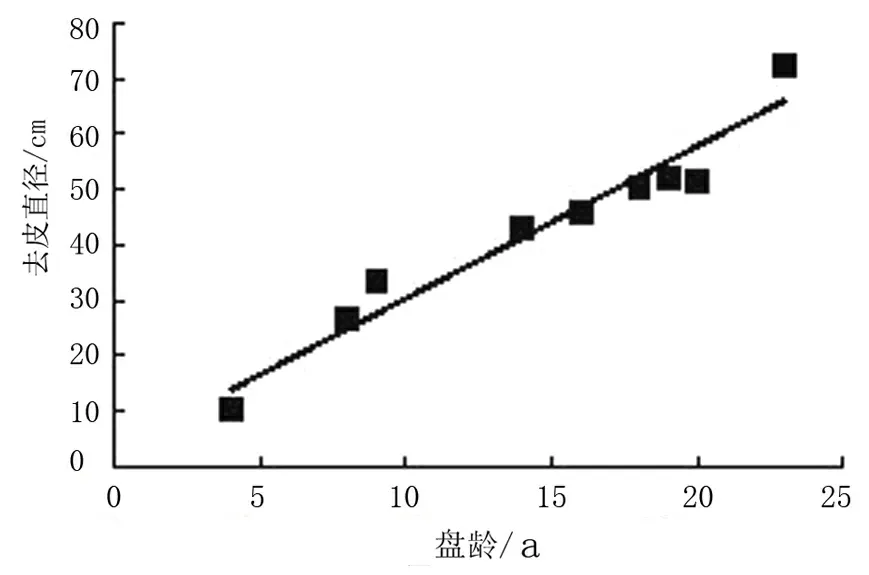
图17 线性模型
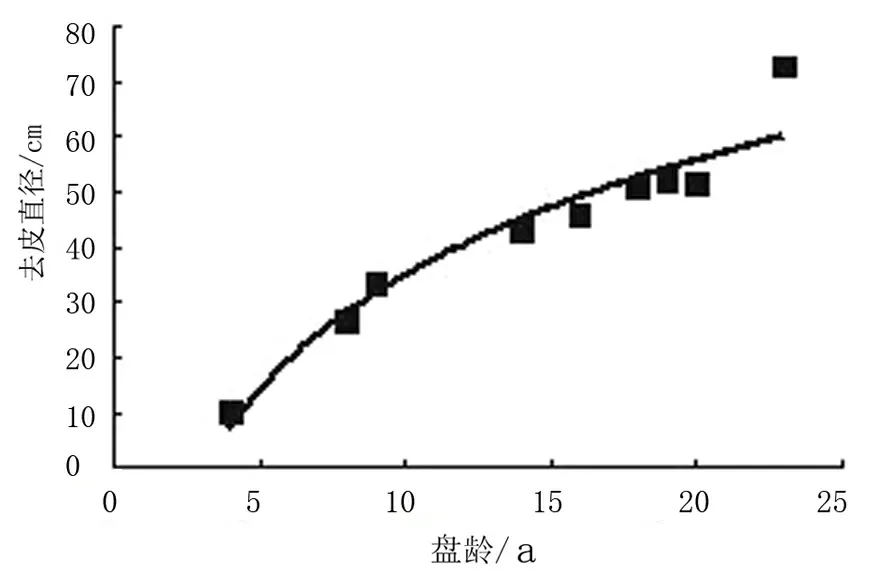
图18 对数模型

图19 二次多项式模型

图20 指数模型
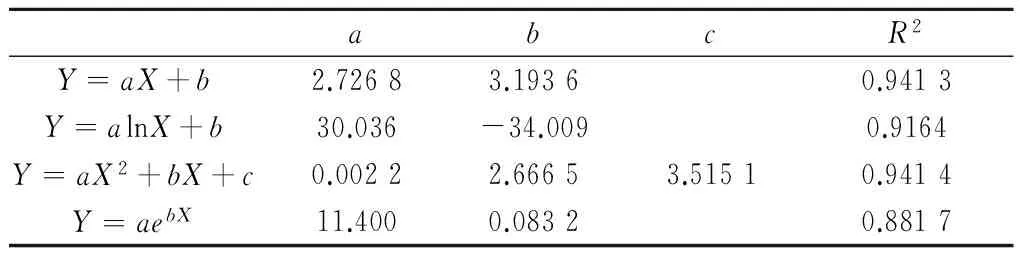
abcR2Y=aX+b2.72683.19360.9413Y=alnX+b30.036-34.0090.9164Y=aX2+bX+c0.00222.66653.51510.9414Y=aebX11.4000.08320.8817
从表5可以看出,无论用哪种模型,计算得到的相关系数都较大。结合图17~图20观察得到,图19的拟合效果最好。因此,在实际应用中,可以二次多项式模型对落叶松进行年轮数-去皮直径关系进行拟合。
4 结论
落叶松树高的生长适合采用二项式模型进行拟合,但与其他模型的拟合效果相差不大,都能达到比较好的拟合效果;
落叶松胸径的生长采用指数和多项式模型拟合比线性和对数模型好,但用不同的模型得到的精度差异不大;
落叶松材积的生长适合采用二次多项式和三次多项式模型进行拟合,预估对数模型和线性模型都不能达到相对较高的拟合精度;
落叶松带皮直径的生长拟合适合采用线性、指数、多项式模型进行,预估都能达到较高的拟合精度;
落叶松去皮直径的生长,虽然选择样本数少,却能达到很好的拟合效果,特别是二次多项式模型,但可信度比落叶松带皮直径模型低;
综上所述,整体来看,采用多项式模型进行模拟的拟合度较高,计算得到的相关系数也较高,因此,可以普遍采用多项式模型来预估落叶松的生长规律。
[1] 李凤日.兴安落叶松天然林直径分布及产量预测模型的研究[J].东北林业大学学报,1991(15):10-11
[2] 王树力,刘大兴.落叶松人工林林分结构与数量成熟龄的研究[J].东北林业大学学报,1992(20):3-4
[3] 孟宪宇.天然兴安落叶松林年龄结构的分析[J].北京林业大学学报, 1989,11(3): 17-23
[4] 葛建平,郭海燕,陈动.小兴安岭天然红松林种群结构的研究[J].东北林业大学学报, 1990,18(6): 26-31
Growth Regularity ofLarixgmeliniiin Dayangqi Forest Farm of Daxing’anling Region
Xian Wenjuan, Yang Zijian, Liang Dan, Liu Lu
(Liaoning Forestry Investigation and Planning Institute, Shenyang 110122, China)
1005-5215(2017)02-0022-05
2017-01-04
先文娟(1988-),女,湖北武汉人,硕士,工程师,现从事林业调查规划工作.
S791.22
A
10.13601/j.issn.1005-5215.2017.02.008

