稠油吞吐中加热半径计算方法及参数的确定

郑爱萍，白秀娟，张玉书，曹海波，林加恩3中石油新疆油田分公司重油开发公司，新疆 克拉玛依

2西安华线石油科技有限公司，陕西 西安

3西部低渗-特低渗油藏开发与治理教育部工程研究中心(西安石油大学)，陕西 西安

稠油吞吐中加热半径计算方法及参数的确定

郑爱萍1，白秀娟1，张玉书1，曹海波2，林加恩31中石油新疆油田分公司重油开发公司，新疆 克拉玛依

2西安华线石油科技有限公司，陕西 西安

3西部低渗-特低渗油藏开发与治理教育部工程研究中心(西安石油大学)，陕西 西安

在稠油吞吐过程中，加热半径是热采中的重要指标，对注汽参数和生产制度起到了指导性作用。运用能量守恒原理，从热量注入方面考虑了蒸汽相变释放的气化潜热，从热量损失方面考虑井筒热量损失和顶底盖层热量损失，最终得到了新的加热半径计算公式。计算结果表明，加热半径受注汽参数、焖井时间、储层参数等因素影响，并系统阐述了岩层各物性参数的计算及选择方法。最后通过实例验证了该方法的计算值和试井解释出的值较为相符，为现场实际应用提供了可靠的方法。

稠油油藏，加热半径，注汽轮次，蒸汽吞吐，热采

Copyright © 2017 by authors, Yangtze University and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).http://creativecommons.org/licenses/by/4.0/

Heavy Oil Reservoir, Heating Radius, Steam Injection Cycle, Steam Soak, Thermal Recovery

1. 引言

在稠油热采中，蒸汽注入参数合理化选择、产量的预测、剩余储量的计算、吞吐过程中的热效率计算，这些都必须知道加热半径，因此加热半径合理计算在热采中起着重要作用。在加热半径计算方面，各学者已做了大量工作，Marx-Langenheim [1]假设油层均质，通过对纵向热损失的研究提出了热采油藏加热面积的计算公式，但未考虑轮次加热；窦宏恩等[2]考虑了轮次加热，但是没有考虑焖井时间对加热半径的影响，也未考虑井筒向地层传热的热量损失；刘鹏[3]有考虑焖井时间对加热半径的影响，但是在推导过程中出现了错误，也未考虑井筒向地层传热的热量损失，在考虑轮次时的加热半径，需要计算上轮次的平均温度，文献[4]认为地层温度不是恒定的，文献[5]认为从井筒到原始地层的温度分布是逐渐降低的，文献[6] [7] [8] [9]对水平井加热半径做了研究。笔者在前者的基础上建立了新的加热半径计算公式，其公式考虑井筒向地层传热的热损失，也考虑焖井时间对顶底层传热的热损失。笔者将各文献的内容进行总结，系统性地得到直井加热半径的求解方法及过程。

2. 数学模型的建立

在蒸汽吞吐中，根据能量守恒原理，热量主要包括4大部分，分别为蒸汽的注入热量、井筒扩散引起的热损失热量、顶底层扩散引起的损失热量、油层吸收热量，如果是多轮次开采还有液体带走的余热。其示意图如图1所示。

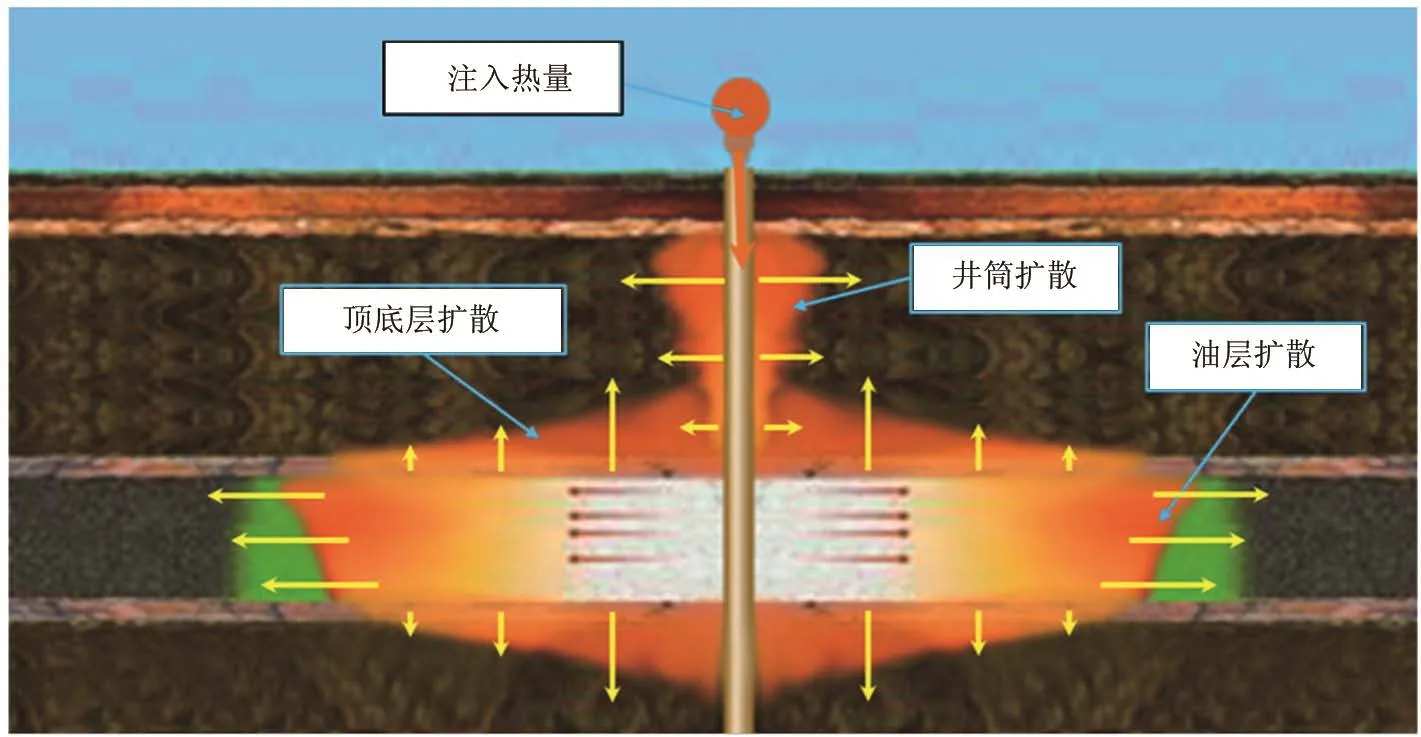
Figure 1. Schematic diagram of energy distribution in thermal recovery process图1. 热采过程中能量分布示意图

2.1. 井筒热损失分析

从井口到井底，热量通过井筒传到地层引起的热损失称为井筒热损失，曾玉强[8]研究了井筒热损失计算公式并作了详细推导，这里只引用其计算公式。

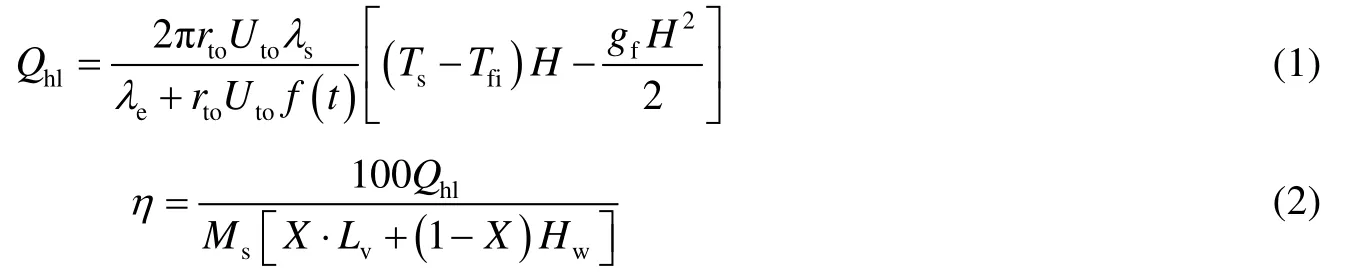
式中：Qhl为蒸汽注入井筒过程中的热量总损失，W；Uto为井筒总传热系数，W/(m2∙K)；rto为油管外半径，m；Ts为蒸汽温度，K；λe、λs都为油层导热系数，单位分别是 W/(m∙K)、kJ/(h∙m∙k)；Tfi为地表的温度，K；H为井深，m；f(t)为Ramey时间函数；η为井筒热损失率，%；Ms为注入的蒸汽质量流速，kg/h；Hw为井口注入温度下水的热焓，kJ/kg；X为井底蒸汽干度，%；Lv为蒸汽的汽化潜热，kJ/kg；gf为静温梯度，℃/100 m。

2.2. 考虑焖井时间对顶底层扩散的影响

顶底层扩散引起的热损失从注汽到生产都存在，笔者之研究焖井段顶底层热损失，刘鹏[3]在研究热量向顶底层扩散时，公式推导过程中出现了错误，笔者做了重新的推导，推导过程如下：

导热速度为：

式中：ql为顶底层导热速率，kJ/h；Tr为加热区温度，℃；αe为顶底层扩散系数，m2/h；Ti为原始地层温度，℃；tm为焖井时间，h。

顶底层扩散热量Qd为：

刘鹏[3]给出了加热区温度与注汽温度的关系：

式中：R为计算半径，m；Re为供给半径，m；Rw为井筒半径，m；Ts为注汽温度，℃。联立式(3)～(5)求解出顶底层热量损失为：

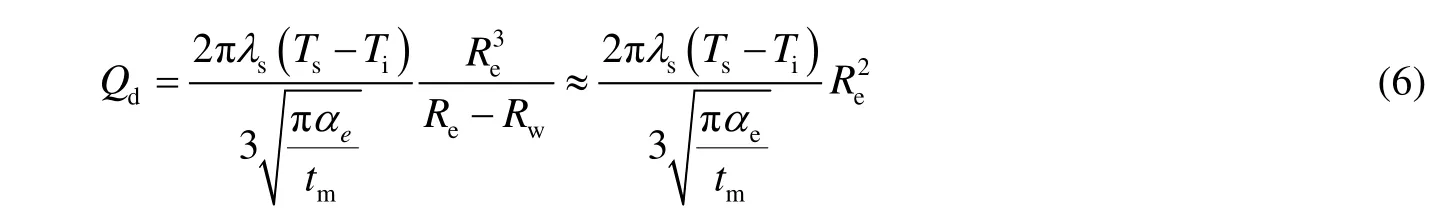
2.3. 加热半径计算公式

油层吸收热量：

式中：h为油层厚度，m；Mr为油层的热容量，kJ/(m3·℃)；Qy为油层吸收热量，kJ；Qz为注入热量，kJ；tz为注蒸汽时间，h；qs为注汽速率，kg/h。

将式(1)～(8)联立求解得到如下公式：

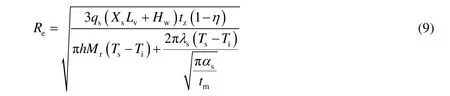
如果考虑轮次，需计算上一轮次带走的余热，其加热半径计算公式为：

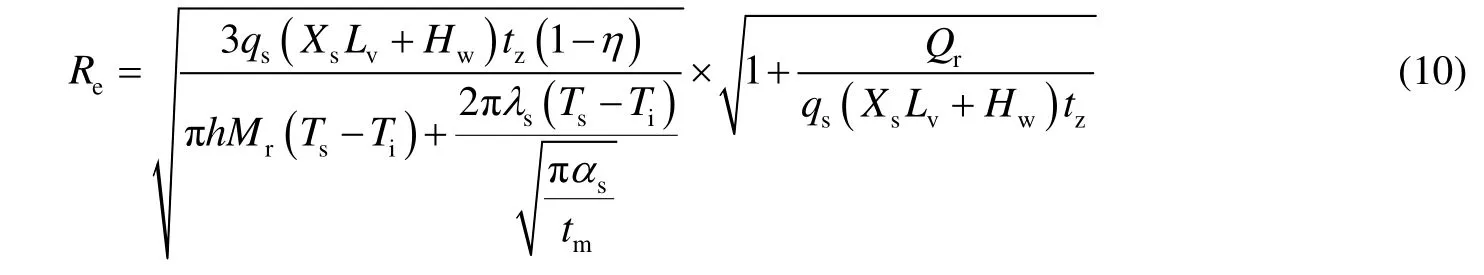
其中：

式中：Qr为上一轮次的余热，kJ；Rn-1为上一轮次的加热半径，m；Tavg为加热区的平均温度，℃。平均温度计算比较复杂，其李春兰[10]给出了较为简单的平均温度计算公式：

式中：Tah为焖井结束后加热半径边缘的温度，℃，一般根据黏温曲线得到，即稠油变为稀油的临界温度；

Taw为焖井结束后井底温度，℃。

3. 参数的选择

地层的参数对加热半径计算准确性影响较大，通过试验方法得到其参数比较困难，因此需通过计算得到其相关参数，文献[11]给出了相关公式。

3.1. 热容量的确定

稠油区的比热反映了地层吸收热量的能力，它是计算加热半径的重要参数，其准确度直接影响加热半径计算的准确度，可根据岩石的组成进行分解得到，如图2所示。

Figure 2. Schematic diagram of reservoir composition distribution图2. 储层成分分布示意图

其热容量计算公式如下：

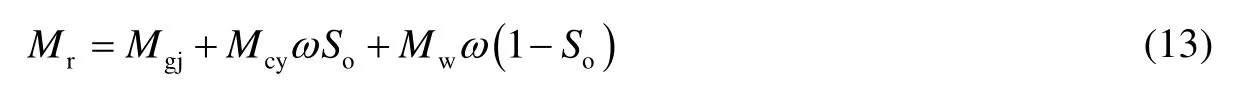
式中：Mgj为岩层骨架热容量，kJ/(m3∙℃)；Mcy为稠油热容量，kJ/(m3∙℃)；Mw为水的热容量，kJ/(m3∙℃)；ω为孔隙度，1；So为含油饱和度，1。

3.2. 导热系数确定

对于计算胶结砂岩建议用Tikhomirov公式，其公式如下：

式中：T为温度，℃；ρr为干燥岩石的密度，g/cm3；Sl为液体的饱和度，1。

3.3. 岩石的热扩散系数

岩石的热扩散系数不是一个独立参数，是其导热系数与热容之比，计算公式如下：

4. 实例分析

新疆某稠油油藏其井深h = 256 m；注汽温度Ts= 280℃；注汽速率qs= 5500 kg/h；注汽压力2.5 MPa，注汽干度X = 0.65，每轮注汽时间tZ= 240 h，焖井时间tm= 72 h；储层厚度为7.8 m；岩层骨架比热Mgj=1154 kJ/(m3·℃)；稠油比热 Mcy= 2120 kJ/(m3·℃)；水的比热 Mw= 4200 kJ/(m3∙℃)，孔隙度 ω = 0.26；含油饱和度So= 0.65；干燥岩石的密度ρr= 2.7 g/cm3；原始地层温度Ti= 35℃。通过以上参数计算加热半径，其求解过程如下。

1) 计算参数的获取

通过以上条件，计算或查表得到以下参数，如表1。

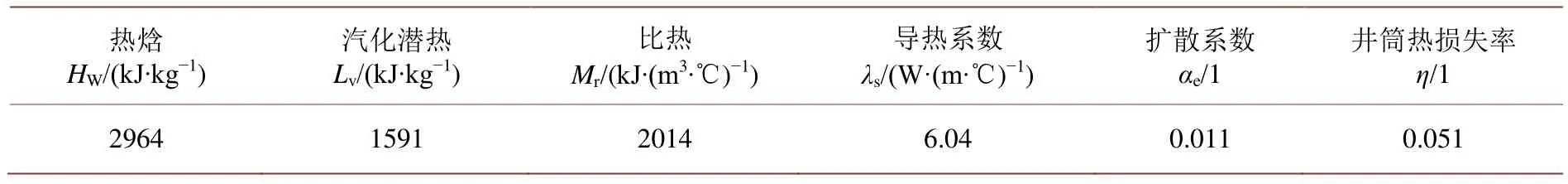
Table 1. Calculation table of parameters results表1. 参数结果计算表

2) 地层平均温度确定

根据黏温曲线(图3)可以看出稠油的黏度突变温度为60℃，Tah为60℃，在焖井结束时刻，井底温度Taw为80℃。每一轮次的井底温度不同。本实例只取某一轮次作为参考。

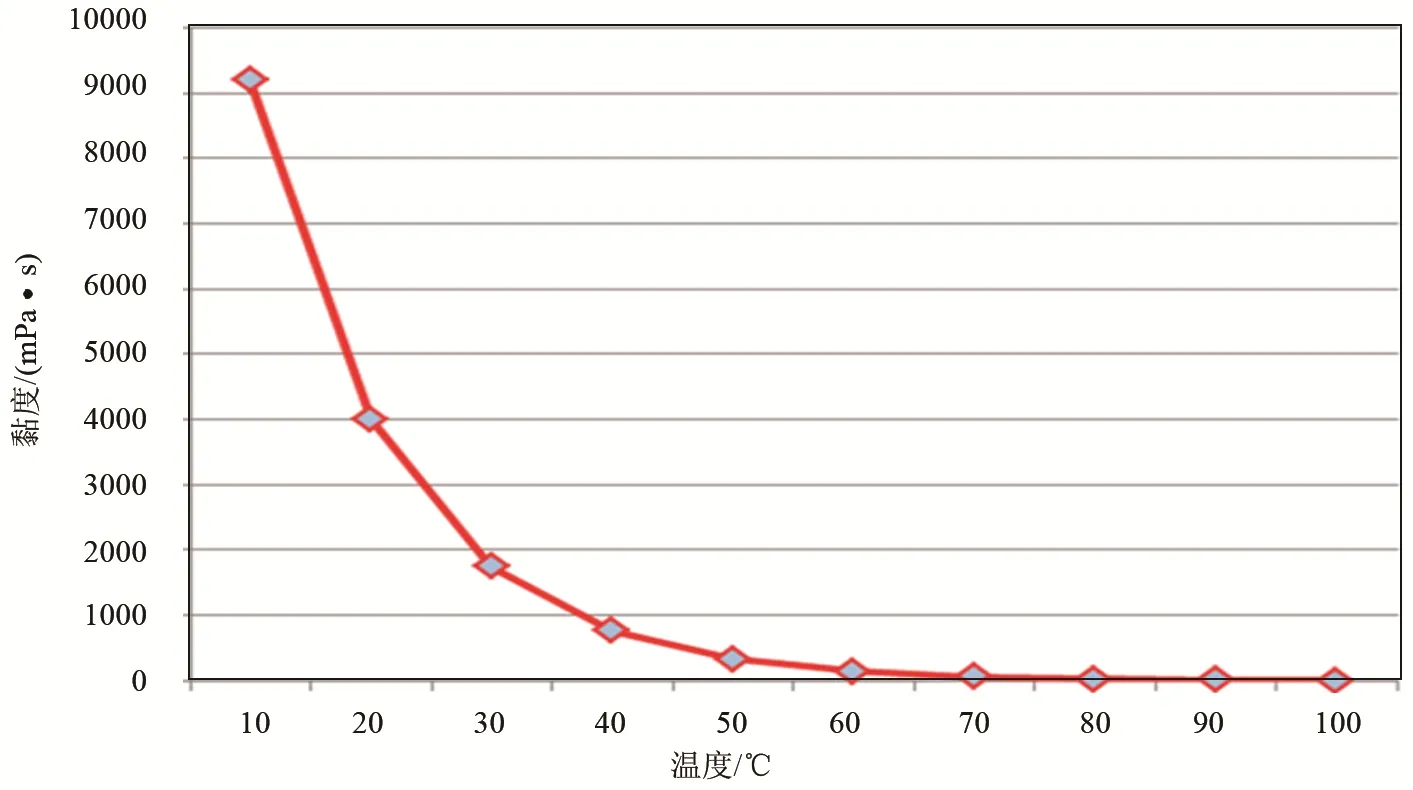
Figure 3. Viscosity-temperature curve in each round图3. 各轮次黏温曲线图

3) 实例计算

通过以上确定出各参数，将这些参数代入式(10)得出加热半径的计算结果，然后将计算值与稠油试井测试得到的值进行比对，其结果是如表2所示。

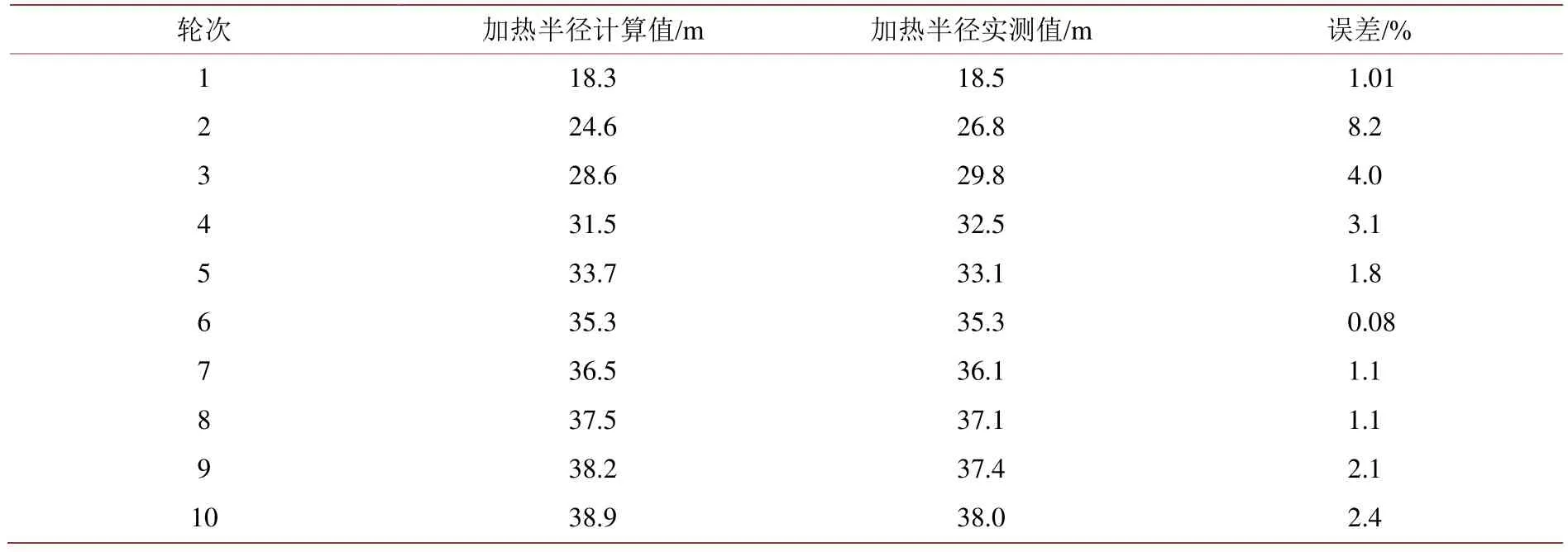
Table 2. Comparison table of calculation results表2. 计算结果对比表

对比图如图4所示。

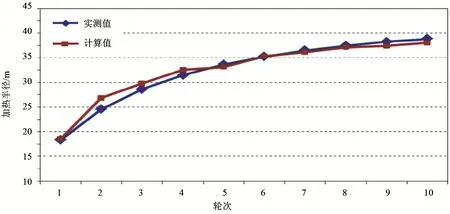
Figure 4. Comparison chart of heating radius calculation results图4. 加热半径计算结果对比图

通过对比分析中，可以看出计算值与实测值曲线符合较好，误差在8%以内，因此该模型可以应用于稠油加热半径的计算中。

5. 结论

1) 运用能量守恒原理，从热量注入方面考虑了蒸汽相变释放的气化潜热，从热量损失方面考虑了井筒热量损失和顶底盖层热量损失，系统性地得到了加热半径的求解方法及求解过程。

2) 新的加热半径计算方法考虑因素全面，通过实例计算和分析表明该方法有较好的精度，可满足工程要求。

3) 阐述了计算加热半径时储层参数比热、导热系数、扩散系数的计算方法。加热半径计算公式从热量注入和热量损失方面考虑因素全面，计算较为准确，可较好地应用于现场实例分析中。

参考文献 (References)

[1] Marx, J.W. and Langenheim, R.H. (1959) Reservoir Heating by Hot Fluid Injection Petroleum Transactions. AIME,312-315.

[2] 窦宏恩, 常毓文, 于军, 等. 稠油蒸汽吞吐过程中加热半径与井网关系的新理论[J]. 特种油气藏, 2006, 13(4):58-61.

[3] 刘鹏. 热采井加热半径及产能方法研究[J]. 科学技术与工程, 2011, 17(11): 3934-3936.

[4] Ramey, H.J. (1962) Wellbore Heat Transmission. Journal Petroleum Technology, 14, 427-435.https://doi.org/10.2118/96-PA

[5] Mattar, L. and Anderson, D.M. (2003) A Systematic and Comprehensive Methodology for Advanced Analysis of Production Data. SPE Annual Technical Conference and Exhibition, 5-8 October 2003, Denver, SPE 84472.https://doi.org/10.2118/84472-ms

[6] 刘春泽, 程林松, 刘洋, 等. 水平井蒸汽吞吐加热半径和地层参数计算模型[J]. 石油学报, 2008, 29(1): 101-105.

[7] 刘东. 热采水平井加热半径计算新模型[J]. 中国海上油气, 2015, 27(3): 84-90.

[8] 倪学锋, 程林松. 水平井蒸汽吞吐热采过程中水平段加热范围计算模型[J]. 石油勘探与开发, 2005, 32(5):108-112.

[9] 曾玉强, 李晓平, 陈礼, 等. 注蒸汽开发稠油油藏中的井筒热损失分析[J]钻采工艺, 2006, 29(4): 44-47.

[10] 李春兰, 程林松. 稠油蒸汽吞吐加热半径动态计算方法[J]. 新疆石油地质, 1998, 19(3): 247-249.

[11] 张锐. 稠油热采技术[M]. 北京: 石油工业出版社, 1999.

[编辑]黄鹂

The Calculation of Heating Radius and Determination of Parameters in Heavy Oil Steam Stimulation

Aiping Zheng1, Xiujuan Bai1, Yushu Zhang1, Haibo Cao2, Jiaen Lin31Heavy Oil Production Company, Xinjiang Oilfield Company, PetroChina, Karamay Xinjiang
2Xi’an Sinoline Petroleum Science & Technology Co. Ltd., Xi’an Shaanxi
3MOE Engineering Research Center of Development & Management of Western Low &Ultra-Low Permeability Oilfield (Xi’an Shiyou University), Xi’an Shaanxi

Jun. 14th, 2016; accepted: Sep. 30th, 2016; published: Jun. 15th, 2017

Heating radius was an important index in the thermal recovery process of heavy oil steam stimulation. It was the guidance for the selection of steam stimulation parameters and production system. The vaporization latent heat of steam phase changes in terms of heat injection and heat losses on the wellbore and of the caprock on the top and the bottom were taken into consideration based on the principle of heat conservation; a new calculation formula of heating radius was established. The calculation result shows that the heating radius is affected by steam injection parameters, soak time, reservoir parameters and other factors. At the same time, the calculation and selection of the physical parameters of rock strata are systematically expounded. The method is finally verified with representative examples, the calculated value is in good agreement with that of well testing interpretation, and it provides a reliable method for the practical application in oilfields.

郑爱萍(1973-)，女，硕士，高级工程师，现从事稠油热采开发、油藏地质研究等工作。

2016年6月14日；录用日期：2016年9月30日；发布日期：2017年6月15日

文章引用:郑爱萍, 白秀娟, 张玉书, 曹海波, 林加恩. 稠油吞吐中加热半径计算方法及参数的确定[J]. 石油天然气学报, 2017, 39(3): 61-68. https://doi.org/10.12677/jogt.2017.393029