方格网法土方计算精度提高的改进方法

田旦，成国辉，徐景，熊仕稳

(长沙市规划勘测设计研究院，湖南 长沙 410007)

方格网法土方计算精度提高的改进方法

田旦*，成国辉，徐景，熊仕稳

(长沙市规划勘测设计研究院，湖南 长沙 410007)

用方格网法进行土方计算，成果直观，便于客户对计算结果进行检核，但传统的方格网法计算精度无法有效保证，尤其是在遇到特殊地形时(如较大陡坎、斜坡穿过格网)，计算结果存在较大误差。为此，本文设计了一种改进的计算方法，根据测区内实测地形构建不规则三角网生成DEM模型，在遇到特殊地形时将方格网进行自动切割，同时通过模型自动获取各方格网点的高程，再对分割好的格网进行土方计算。实例表明该方法提高了方格网法土方计算的精度。

方格网法；格网切割；不规则三角网；数字地面模型

1 引 言

传统的方格网法土方测量需要放样出方格网点，然后测出每个方格网点的高程，再根据方格四个角点高进行土方计算。由于该方法简单实用，成果直观，同时便于检核，是客户首选的土方计算方法[2]。但是该方法的外业工作效率较低，单个的方格网角点高程也无法准确反映出周边区域的地形高程特征，尤其是当陡坎或者变坡从方格网中间穿过时(如图1所示)，用传统方格网法进行方量计算会导致该区域的方格方量产生较大误差，甚至错误。为了既能满足客户需求方格网的计算成果的要求，同时又能保证土方计算的精度，本文设计了一种改进的方格网法土方测量计算方法：在野外作业时不需要进行格网放点，根据实际情况进行地形测量，内业根据所测地形利用不规则三角网进行建模，在遇到特殊地形时根据实际情况将方格网进行自动分割，同时通过模型自动获取各方格网点的高程，再对切割好的格网进行土方计算。

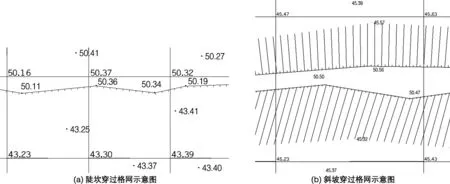
图1 土方放样格网示意图

2 改进方法的作业流程及关键技术

改进方法作业流程如图2所示。

要实现上述改进方法来提高土方计算的精度，关键在于实现以下两点，一是要生成与实际地形相吻合的数字地面模型，以此来确保格网点取高正确合理，二是在遇到格网内有特殊地形时，通过格网切割分块计算来确保方量计算的正确性。下文将对如何实现这两个关键技术点进行详细的探讨。

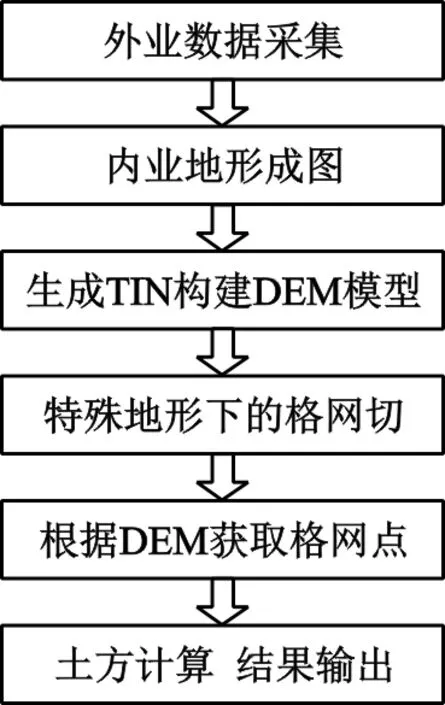
图2 改进方法作业流程

2.1 DEM模型的建立

要确保格网高程点获取的正确，关键是要有一个准确的DEM模型，而要建立一个准确的DEM模型需要注意如下几个关键点：

(1)外业数据采集。外业数据采点时依据实际地形进行测点，测点要到位，同时要特别注意坎下、池塘底、水沟底等等均需要采集高程点。

(2)内业地形成图。为了确保后续生成三角网的正确性，在绘制地形图时首先要剔除粗差，同时必须确保绘制的每个地物地貌要素上要有正确的高程值。

(3)构造合理的不规则三角网。为了生成与实际地形相吻合的数字高程模型，必须事先构建合理的三角网，而通过软件自动构建的三角网往往不合理，从图3可以看出模型自动生成的三角网穿过了斜坡及陡坎，显然这样的构网是不合理的，因此在构网时需要进行必要的人工干预，比如添加特性线，即在坎下、坡下等添加带有高程的特性线，避免三角形穿过地形特性线，使构建的模型更加真实合理，需要添加特性线加以约束的地形地貌包括坎、坡、沟、自然形态的山等[3]。图4经过特征线的添加后，三角网未穿过斜坡及陡坎，构网正确合理。

图3 未进行调整的三角网

图4 调整后的三角网

2.2 特殊地形下的格网切割

从图5可以看出，由于方格网法只考虑了四个角点的高程进行土方计算，在遇到斜坡穿过格网时，导致方格网中间斜坡的方量被忽略，方量计算结果产生很大的偏差。为此，通过自编程序，对含有特殊地形的格网依据实际地形进行自动分割，然后对格网分块计算，以确保土方计算结果准确。图6根据斜坡形状将方格网进行切割，通过DEM模型自动获取各格网点的高程，然后对切割后的格网进行分块方量的计算，确保了方量计算的正确性。

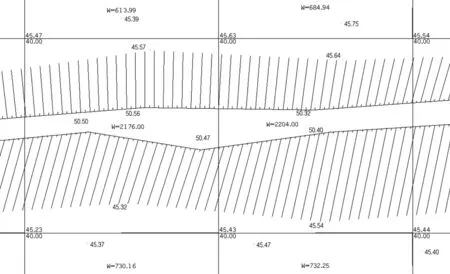
图5 未进行切割的方格网

图6 切割后的方格网

3 实 例

本文以长沙某10*10土方测量项目为例，按照本文建立DEM模型需要注意的关键点进行土方测量的外业数据采集。内业计算软件采用清华山维与我院共同开发的基于EPS2008平台下的长沙土方计算模块，同时通过自编程序实现方格网的自动切割及格网点高程自动获取，以提高土方量的计算效率和精度。

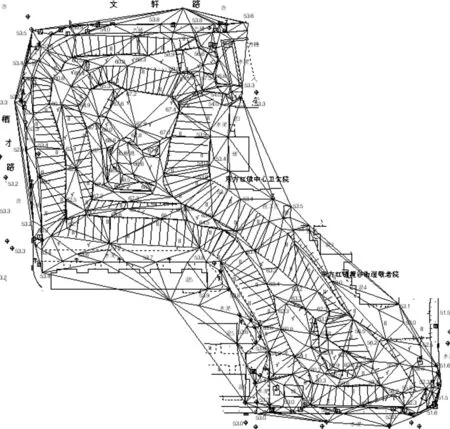
图7 土方原地貌及三角网

在EPS2008长沙管线模块中构建三角网，生成与实际地面相吻合的DEM模型(原始地貌及三角网如图7所示)。由于DEM法进行土方计算不受场地地形限制，且精度较高，其计算结果接近真实值[4]，因此本文选取DEM计算结果作为本实例实际土方量的参考值，以检核本文提出的改进方法的有效性。

分别对未进行格网切割及对格网进行切割后方量进行计算，得到的结果与DEM法计算的参考方量进行比较，对比结果如表1、2所示。

未切割格网计算方量与参考值对比表(单位/m3) 表1

切割格网计算方量与参考值对比表(单位/m3) 表2

表1与表2结果表明，在遇到有陡坎及斜坡等特殊地形时，用格网法计算方量误差较大，挖方量和填方量与参考值的相对误差分别为17.89%和14.21%；而利用本文设计的改进方法，根据实际地形，按照较大陡坎及斜坡的走向自动对方格网进行切割，同时根据DEM模型获取各格网点高程后，再进行土方计算，挖方量和填方量与参考值的相对误差下降为1.70%和5.00%，极大地提高了土方计算的精度。

4 结 论

本文设计了一种改进的方格网土方量计算方法，能在特殊地形下依据地形对方格网进行自动切割，并依据DEM模型进行格网点高程自动获取并进行分块土方计算，既满足了客户对方格网土方成果的实际需要，又保证了在复杂地形下土方计算结果的正确性。实例表明，该方法有效可靠，提高了场地内含有较大陡坎、斜坡等特殊地形条件下土方计算的精度。

[1] CJJ/T 8-2011. 城市测量规范[S].

[2] 雷松，王海英，艾云毅. 方格网法与三角网法相结合准确计算土方量[J]. 城市勘测，2011(6)：154～156.

[3] 匡志威，张翠峰，刘鹏程等. 带特征线的TIN生成及应用[J]. 城市勘测，2012(5)：120～122.

[4] 罗德仁，邹自力，汤江龙. 工程土方量计算比较分析[J]. 东华理工学院学报，2005(3)：59～64.

[5] 王铁生，程鹏里，赵东保等. 方格网法土方量计算及误差影响[J]. 测绘通报，2012(S)：109～111.

[6] 张敏捷. 基于EPS平台的土方测算方法探讨以增城市某人工湖开挖工程为例[J]. 测绘与空间地理信息，2013(5)：205～207.

[7] 北京清华山维新技术开发有限公司. EPS 2008地理信息工作站使用说明书[R]. 2010.

An Improved Method for the Accuracy of Earthwork Calculation from Grid Network

Tian Dan，Cheng Guohui，Xu Jing，Xiong Shiwen

(Changsha Planning & Desing Survey Research Institute，Changsha 410007，China)

Earthwork calculation with gird network makes the production more visual，which could be helpful for customers to easily look over the production quality，however，the traditional grid network is hard to effectively ensure the production accuracy，and especially with a low accuracy in a special terrain (e.g. steep scarp or slope across the grid network). In this paper，we develop an improved method for the earthwork calculation by grid network，which will take into account the real landform to construct the DEM model in the measuring region. In our new method，the grid can be automatically cut in the special terrain，and the elevation of the grid network can be automatically extracted by the model，then the earthwork volume was calculated. To assess this new method for the accuracy of earthwork calculation，we give a case study in this paper，and it demonstrates a greater improvement of accuracy than the traditional grid network.

grid network；grid cutting；triangulated irregular network；DEM

1672-8262(2017)03-148-04

P209，P258

B

2016—12—23

田旦(1984—)，男，工程师，硕士，主要从事城市测量方面的技术工作。

江西省数字国土重点实验室开放研究基金资助项目(DLLJ201705)