轧机液压AGC-LP耦合系统的H∞控制器设计
鲁凌云,李维刚,2,黄卫华,严保康
(1.武汉科技大学信息科学与工程学院,湖北 武汉,430081;2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉,430065)
轧机液压AGC-LP耦合系统的H∞控制器设计
鲁凌云1,李维刚1,2,黄卫华1,严保康1
(1.武汉科技大学信息科学与工程学院,湖北 武汉,430081;2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉,430065)
根据热连轧机自动厚度控制(AGC)系统和液压活套控制(LP)系统各自的特点,结合这两个子系统的模型,建立液压AGC-LP耦合系统模型。参照广义系统的标准选取了合适的控制目标,基于H∞控制理论对组合系统进行分析,采用MATLAB鲁棒控制工具箱中线性矩阵不等式(LMI)求解方法设计了H∞状态反馈控制器,使得系统达到性能指标最优。将使用H∞控制器与传统PID控制器的AGC-LP耦合系统进行仿真比较,结果表明,使用H∞控制器的系统有更好的动态和稳态性能,两个子系统相关变量的耦合也有所改善。
热连轧机;AGC;活套系统;H∞控制器;LMI;解耦
为了保证轧制过程的顺利进行,现代主流的热连轧机大都通过液压活套装置(LP)的缓冲作用来吸收咬钢过程中形成的套量,并保持恒定的小张应力控制,同时通过自动厚度控制系统(AGC)来提高带钢厚度控制的精度。由于张应力的变化是引起带钢厚度变化的主要原因之一,因此AGC-LP系统的控制难点在于LP系统的高度控制和张应力控制之间的耦合以及AGC系统与LP系统之间的相互影响。现有对AGC-LP系统耦合的研究大都考虑了组合系统的线性成分和非线性成分,并改善了系统的鲁棒性,但组合模型强耦合非线性的特性为系统的解耦带来了困难。
由于H∞控制理论考虑了实际系统与数学模型之间的不确定性,降低了系统建模的复杂程度,且H∞方法将复杂的系统解耦问题转换成了线性矩阵不等式求解问题,并且利用MATLAB的LMI工具箱可以精确地求解,为此,本文基于H∞控制理论对AGC-LP耦合模型进行控制器设计。首先,根据AGC和LP系统子模型建立了AGC-LP耦合系统模型,然后通过H∞控制方法为AGC-LP控制系统设计了状态反馈控制器,最后对给定输入信号下组合系统的输出响应进行仿真,并通过与传统PID控制器相关性能指标的比较来验证所设计控制器的有效性。
1 AGC-LP耦合系统模型的建立
以热连轧机相邻机架作为分析对象,涉及到的变量参数如图1所示。图1中,l1和l2分别为活套支撑辊接触面到Fi机架出口和Fi+1机架入口的距离;σ为Fi机架出口带钢张应力;H和h分别为Fi机架入口和出口的带钢厚度;vi和vi+1分别为带钢在Fi机架的出口速度和Fi+1机架的入口速度;R为轧辊的半径;θ1和θ2分别为Fi机架出口和Fi+1机架入口的连线与轧线之间的夹角;l为活套臂长;θ为活套高度角;a为活套器中心到相邻机架的直线距离;L=2a;ω为轧辊的角速度;d为活套支撑辊与轧线的距离。
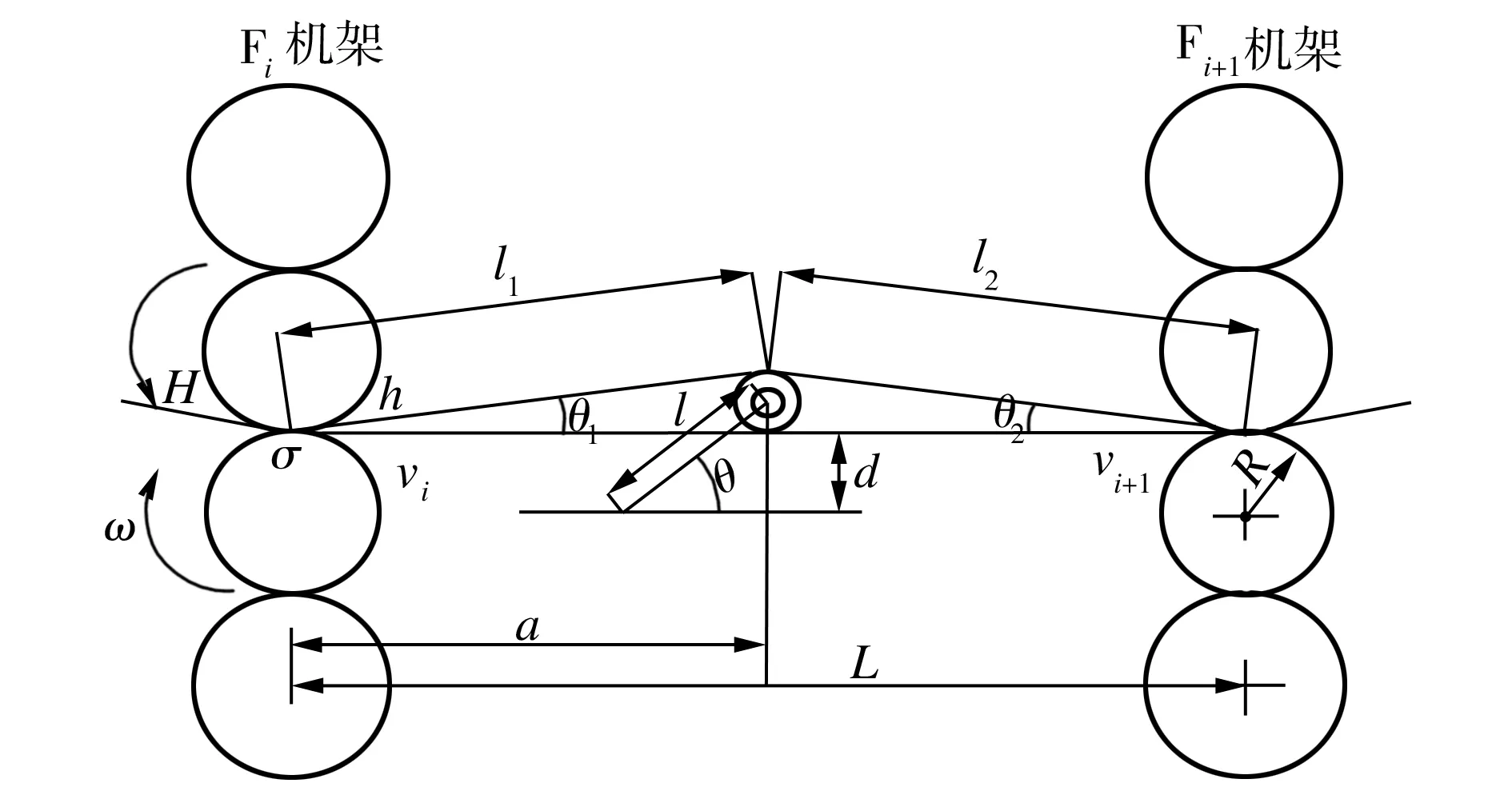
图1 活套机构参数示意图
1.1 液压阀控缸系统的建立
LP系统和AGC系统均由液压阀控缸驱动,两者的液压阀控缸模型相同,只是负载和对象不同。关于阀控缸的建模过程详见文献[1],其中几个关键方程如下:伺服阀的动态特性可以用一个二阶振荡环节来描述:
(1)
式中:Gv为传递函数;s为拉普拉斯算子;ωv为伺服阀的截止频率;δv为伺服阀阀芯的阻尼系数。
液压缸的流量方程为
QL=KqXv-KcΔPL
(2)
式中:Kq为伺服阀的流量增益系数;Kc为伺服阀的流量压力系数;Xv为伺服阀的位移量;ΔPL为系统压力与回油压力之差。
根据牛顿第二定律,液压缸的运动方程为
(3)
式中:Apst、Arod分别为液压缸无杆腔和有杆腔的横截面积;Ppst、Prod分别为液压缸无杆腔和有杆腔的压力;M为负载的等效质量;B为运动黏滞系数;G为弹性阻力系数;y为活塞位移;t为时间;fLd为负载作用力。
1.2 AGC系统模型
Fi机架出口带钢厚度可用弹跳方程来表示,弹跳方程给出了活套张应力与活套高度hi的关系[2]:

(4)
式中:S为辊缝设定值;Bw为带钢宽度;Y为变形抗力系数;Q为应力状态系数;τ为入口带钢张应力;C为轧机刚度系数。
对于AGC系统来说,式(3)所示力平衡方程中ΔF即为系统提供的轧制力。如果只考虑轧件变形抗力而忽略其他因素,则负载作用力fLd可以表示为
(5)
若忽略轧机的轧辊偏心量Δx,则轧件的出口厚度h便等于工作辊的负载辊缝SL,而SL为
(6)

1.3 LP系统模型的关键方程
设第Fi机架的出口速度为Vout(i),第Fi+1机架的入口速度为Vin(i+1),那么活套的套量Lloop可以表示为
(7)
张应力σ可以表示为
(8)
式中:E为材料的弹性模数。
热连轧自动厚度控制过程中,对活套的补偿有本架补偿和后架补偿两种方式,采取后架补偿即在第Fi+1机架投入AGC能获得更高的速度补偿精度,因此有如下的速度补偿公式[3]:
(9)
式中:vi为Fi机架带钢的出口速度;vRi为Fi机架的轧辊速度;vi+1为Fi+1机架带钢的入口速度;vR(i+1)为Fi+1机架的轧辊速度;fi为Fi机架的前滑值;βi+1为Fi+1机架的后滑值。
由式(7)~式(9)可得活套套量和带钢速度以及张应力的关系为
(10)
式中:
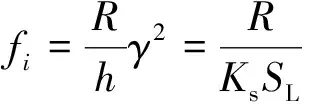
活套的角加速度与综合力矩M密切相关,对于活套有如下的力矩平衡关系:
(11)
(12)
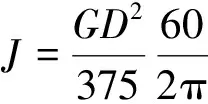
1.4 AGC-LP模型的建立
综合式(1)~式(12),已经找出了关联变量,建立起了自动厚度控制系统与活套系统的联系。将AGC系统写成状态空间表达式,选取辊缝SL、带钢速度V、活套输出力矩M作为输入控制量,即u=[u1u2u3]T=[SLVM]T,令张应力σ、活套高度角θ、轧辊角速度ω作为状态变量,即x=[x1x2x3]T=[σθω]T,以带钢出口厚度h、张应力σ和活套高度角θ作为输出量,即y=[y1y2y3]T=[hσθ]T,则可得AGC-LP的状态方程为
(13)
输出方程为
(14)
2 H状态反馈控制器设计
将AGC-LP系统视作如图2所示的广义系统,其中P(s)为系统状态空间矩阵,K为反馈控制器矩阵,K(s)为控制器的传递函数。整个闭环系统由以下的状态空间描述:
(15)
式中:x∈n为状态向量;u∈n为控制输入;y∈p为测量输出,A、C1、C2为系统状态变量的系数矩阵;B1、D11、D21为系统扰动的系数矩阵;B2、D12、D22为系统输入的系数矩阵。
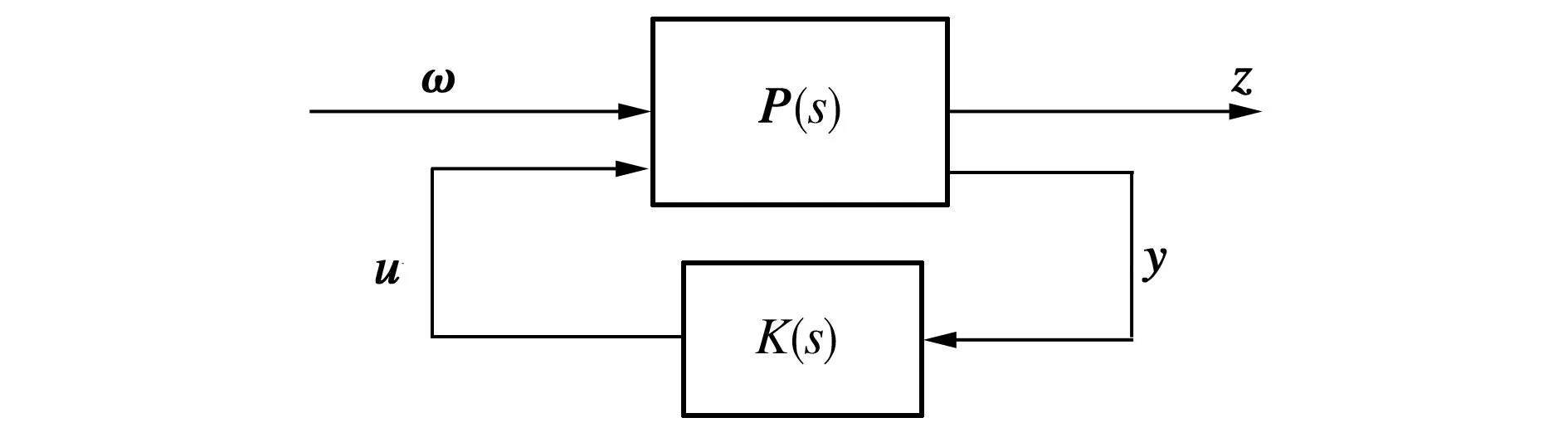
图2 广义系统
由于AGC-LP系统是可观测的,因此y较容易得到;在H∞控制器的设计过程中,测量输出都是作为系统的反馈输入,z∈r是有限大的被调输出,也是在系统的仿真过程中所得到的输出响应;ω∈q为具有有限能量的外部扰动,这里将以有限能量的白噪声作为外部扰动。
H∞控制的目的就是设计一个控制器u(s)=K(s)y(s),使得闭环系统满足以下性质:
(1)闭环系统是内部稳定的,即闭环系统状态矩阵的所有特征值均在左半开复平面中。
(2)从扰动输入ω到被调输出z的闭环传递函数Twz(s)的H∞范数小于1,即
(16)
具有这样性质的控制器u(s)=K(s)y(s)称为式(15)所示系统的一个H∞控制器[2]。
传统的活套系统都采用PID控制器,没有考虑活套高度和张应力之间的相互作用,系统的抗扰动性能有所欠缺。相比之下,H∞状态反馈设计是在Ricatti方程的求解条件上增加由Bode积分定理所规定的鲁棒性约束,即达到式(16)所要求的性能指标,以此为目标来设计H∞反馈控制以消除建模误差和对象零极点漂移的影响。
由于系统的状态是可以直接测量到的,因此采用H∞状态反馈控制器。首先,要满足以下的反馈控制率:
u=Kx
使得相应的闭环系统
是渐近稳定的。
闭环传递函数Twz(s)的H范数满足:
(17)
当且仅当存在一个对称正定矩阵X和矩阵W,使得矩阵不等式
(18)
成立,则u=W*(X*)-1x是式(15)所示系统的一个状态反馈H∞控制器[4]。
在加入了H∞状态反馈控制器后AGC-LP系统的框图如图3所示。
要确定矩阵不等式(18)中的各子矩阵,由式(13)可得:

图3 带H∞反馈控制器的AGC-LP系统框图
(19)
取活套高度角为10°,弹性模量E=2.1×105MPa,GD2=1.5×105kN·m;σ=25.9 MPa,L、l1、l2、R分别为6、2.2、1.8、0.8 m,J=78.5 N·m,B=8.5,Bw=0.082,C=8.25,H=0.3m,h=0.156 m,Ks=50,则可求得系统矩阵A、B2、C1,而外部扰动的系数矩阵B1、D11、D12未知;系统的测量输出对应的系数矩阵C2、D21、D22均可通过观测得到。在热连轧系统中,扰动的因素很多,例如温度、轧辊形变等,这些扰动综合起来影响轧制带钢的厚度,基于这一点,用近似的白噪声和正弦扰动来模拟带钢在轧制过程中的厚度波动,则可求得系数矩阵B1、D11。
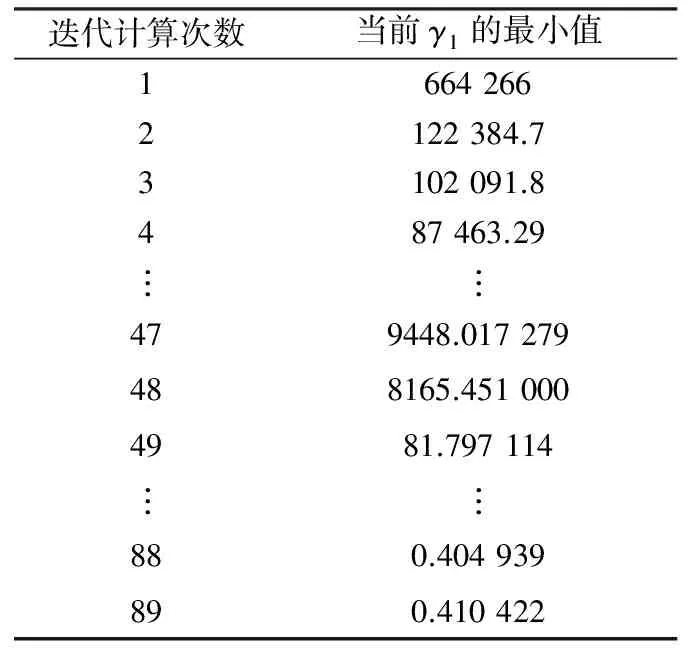
得到了式(19)所需的各个矩阵后,再利用MATLAB的LMI工具箱相关函数进行求解。因为AGC-LP系统的优化问题是一个具有线性矩阵不等式约束的线性目标函数最小化问题,故使用工具箱中的求解器mincx,将AGC-LP系统的状态空间矩阵代入到式(18)的矩阵不等式进行求解。经过反复的迭代运算,得到系统的最优H∞性能指标γ1的值如表1所示。
表1 线性目标在LMI约束下的最小化
Table 1 Minimization of linear target under LMI constraints
迭代计算次数当前γ1的最小值16642662122384.73102091.8487463.29︙︙479448.017279488165.4510004981.797114︙︙880.404939890.410422
最终,γ1达到最小值0.410 422,得到了满足H∞性能指标的最优解,可以求得优化系统性能的闭环反馈控制矩阵,为了方便仿真,再通过MATLAB指令:
[gopt,k]=hinflmi(P,r)
(20)
得到系统的最优H∞控制器K(s),对应的系统矩阵可以由函数[ak,bk,ck,dk]=ltiss(K(s))求得,这样就能得到一个使H∞性能指标γ1最优的控制器矩阵。
3 仿真结果及分析
3.1 H∞控制器与PID控制器对AGC-LP系统响应的影响
采用Simulink软件进行仿真,对使用H∞控制器与PID控制器时AGC-LP系统的输出进行比较。按照图3所示的系统结构搭建闭环仿真框图,主控制器K(s)的系统矩阵和液压AGC-LP的系统矩阵用两个状态空间模块表示,其中主控制器的系统矩阵分别与式(20)所求得的ak、bk、ck、dk相对应。
以鞍钢F3机架出口为例,设定带钢出口厚度为7.52 mm,张应力为25.9 MPa,活套高度角为9°。经过仿真,在持续扰动下,AGC活套系统的张应力、活套高度角、轧件厚度3个变量在传统PID控制和H∞控制下的响应曲线如图4所示。由图4可以看出,对于活套高度角和轧件厚度的响应,使用H∞控制器不但减少了震荡和调节时间,同时活套角的超调量减小,轧件厚度的稳态精度也得到提高,张应力的调节时间由0.9 s缩短到0.6 s。总体上看,H∞控制较PID控制调节时间缩短,过渡过程比较平稳,过渡过程中的震荡次数减少,震荡幅度也有所降低,有效避免了张应力的瞬间突变,超调及响应时间也同时缩短,可以控制热连轧过程尽快进入稳态。
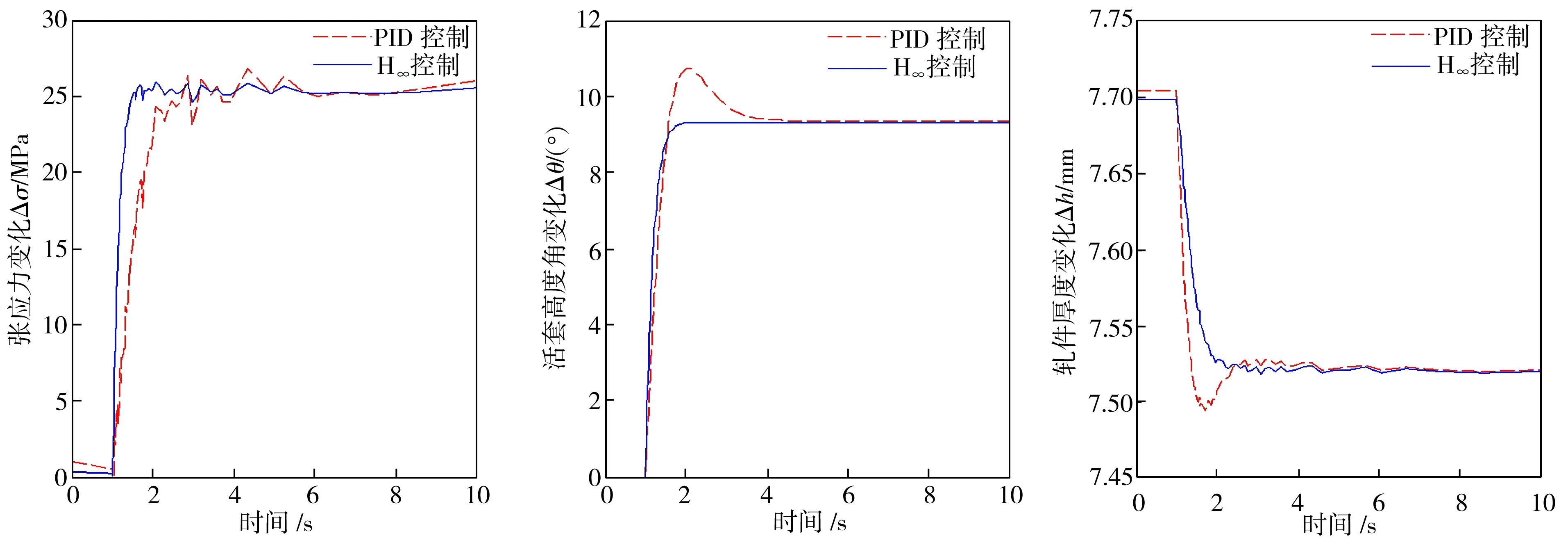
(a)张应力 (b)活套高度角 (c)轧件厚度
图4 系统在H∞和PID控制方式下的输出比较
Fig.4 Comparison of output of system under the H infinity and PID control
3.2 H∞控制器对AGC-LP系统的解耦效果
对活套张应力和活套高度角分别附加1 MPa和3°的阶跃扰动,仿真对比使用H∞控制器和传统PID控制器时AGC-LP系统的响应,以验证H∞控制器对AGC-LP系统的解耦效果,结果如图5所示。由图5中可以看出,与PID控制器相比,本文所设计H∞控制器对AGC-LP系统的解耦有较大的帮助。

(a)高度角受扰时高度角和张应力响应曲线

(b)张应力受扰时高度角和张应力响应曲线
3.3 H∞控制器控制下AGC系统的输出响应
为了验证加入H∞控制器后液压AGC系统的厚度控制效果,按照实际情况,仿真中在带钢进入精轧前施加扰动,主要考虑中间坯头尾厚度波动、温度以及高频随机扰动等干扰信号模拟带钢厚度变化情况。设带钢原始厚度为H0,则带钢厚度的波动可近似表示为

模拟鞍钢集团朝阳鞍凌钢铁有限公司热连轧机组F1~F5机架的出口厚度给定量[5],每一个机架都按照各自的设定给定相应的辊缝、活套高度角以及厚度值,仿真结果如图6所示。由图6中可知,虽然存在来料厚度不均匀以及压力和弹跳的波动等影响因素,但通过H∞控制器控制的AGC系统的调节,机架出口的带钢厚度基本稳定,由此证明了系统模型的准确性与控制器的有效性。

图6 F1~F5机架出口厚度仿真结果
Fig.6 Simulation effort of F1~F5 mills’ outgoing thickness
4 结语
本文研究了基于LMI的状态反馈H∞鲁棒控制方法在AGC-LP控制系统中的应用,通过建立系统的状态空间模型,使用LMI工具箱进行优化求解,让系统性能指标优化的过程更加简便。仿真结果表明采用H∞控制理论设计的控制器不仅可以让系统具有良好的性能指标,还对耦合系统有较好的解耦效果,这对于AGC-LP系统性能的改进有一定的实际意义。
[1] 童朝南,武延坤,宗胜悦,等. 热连轧中液压活套系统数学模型的研究[J]. 系统仿真学报, 2008, 20(6):1381-1385,1389.
[2] 曲蕾,王京. 多变量非线性厚度-活套系统的鲁棒逆控制[J]. 控制理论与应用, 2009, 26(5):562-566.
[3] 童朝南,孙一康,陈百红. 热连轧AGC控制中活套补偿的两种观点[J]. 轧钢, 2002, 19(4):47-48.
[4] 俞立. 鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社, 2002.
[5] 庄野,张辉,刘新婷. 鞍凌热连轧自动厚度控制系统实时仿真[J]. 冶金自动化, 2013, 37(6):54-58.
[责任编辑 郑淑芳]
Design of H∞controller for hydraulic AGC-looper coupling system for hot strip mills
LuLingyun1,LiWeigang1,2,HuangWeihua1,YanBaokang1
(1. College of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430081, China; 2. Hubei Province Key Laboratory of Systems Science in Metallurgical Process, Wuhan University of Science and Technology,Wuhan 430065, China )
According to the characteristics of the automatic gauge control(AGC) system and the looper control system of hot strip mills, a model of the hydraulic AGC-LP system was constructed by the models of two subsystems. The appropriate control target was selected by the criterion of the generalized system to establish the generalized controlled object, and then the H∞state feedback controller was designed to achieve the optimal performance, with the linear matrix inequality(LMI) of robust control toolbox in Matlab. Comparing the PID control system with H∞controll system in simulation, the results show that the system with the designed H∞controller has a better dynamic and static performance, in which the relevant decoupling performance among variables of two subsystem has been improved.
hot strip mill; AGC; looper system; H∞controller; LMI; decouple
2017-03-25
湖北省教育厅科学技术研究计划重点项目(D20161103);武汉市青年科技晨光计划资助项目(2016070204010099);武汉科技大学冶金工业过程系统科学湖北省重点实验室开放基金资助项目(Z201501).
鲁凌云(1993-),男,武汉科技大学硕士生.E-mail:121063261@qq.com
李维刚(1977-),男,武汉科技大学教授,博士.E-mail:liweigang.luck@foxmail.com
10.3969/j.issn.1674-3644.2017.04.008
TP273
A
1674-3644(2017)04-0279-06

