与格林L-关系相关的半环簇研究

王丽丽,王立群

(重庆理工大学 理学院， 重庆 400054)



与格林L-关系相关的半环簇研究

王丽丽,王立群

(重庆理工大学 理学院， 重庆 400054)

半环； 簇； 格林关系

1 引言及预备知识

设(S,+,·)是(2，2)-型代数。若(S,+,·)的加法导出(S,+)和乘法导出(S,·)都是半群，并且(S,+,·)满足等式x(y+z)≈xy+xz和(x+y)z≈xz+yz，则称(S,+,·)是半环。格林关系在半群代数理论的发展中有着至关重要的作用， 而半环是满足分配律的同一集合上的两个半群， 因此有必要对半环上的格林关系进行研究[1-3]。文献[4]对幂等元半环上的格林关系进行了的研究，并借助幂等元半环的格林关系研究了这类半环簇的L-子簇和D-子簇，得到了许多重要的结论。

设(S,+,·)是半环，且满足下列附加恒等式：

xn≈x

(1)

x+x≈x

(2)

(x+y)n-1≈xn-1+yn-1

(3)

(4)

(5)

由文献[3]可知完全正则半群的每个H-类都是群，并且每一个完全正则半群S都是完全单半群的半格S=(Y,Sα)，这里Y与S/J同构，Sα是S的J-类。且有

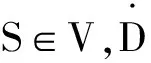
2 主要结果

定理1

1)L0是由以下等式所确定的V的子簇：

xyn-1≈yxn-1yn-1

(6)

2)L1是由以下等式所确定的V的子簇：

xyn-1≈x

(7)

3)L是由以下等式所确定的V的子簇：

(xyn-1+z)(yxn-1yn-1+z)n-1≈xyn-1+z

(8)

(z+xyn-1)(z+yxn-1yn-1)n-1≈z+xyn-1

(9)

zxyn-1(zyxn-1yn-1)n-1≈zxyn-1

(10)

4)L=L1∘L0。

证明 只证明1)，其他情况类似可证。

以下定理的证明比较简单，故省略。

定理2

x+y≈y+x+y

(11)

x+y≈x

(12)

z+x+y+z+y+x+y≈z+x+y

(13)

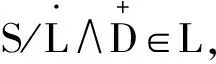
从而

因此：

(abn-1+c)=

(abn-1+c)((abn-1+c)(ban-1bn-1+c)n-1)n-1=

(abn-1+c)(ban-1bn-1+c)n-1

(c+abn-1)=

(c+abn-1)((c+abn-1)(c+ban-1bn-1)n-1)n-1=

(c+abn-1)(c+ban-1bn-1)n-1

(cabn-1)=

(cabn-1)((cabn-1)(cban-1bn-1)n-1)n-1=

(cabn-1)(cban-1bn-1)n-1所以S满足等式(8)～(10)。因此，由定理1得：S∈L。

a=abn-1,b=ban-1

从而

an-1=(abn-1)n-1=an-1(bn-1)n-1

bn-1=bn-1(an-1)n-1

cn-1+an-1cn-1+cn-1bn-1)=((an-1+

cn-1+cn-1bn-1)

因此有

从而推出

即有

cn-1an-1=cn-1an-1+cn-1bn-1+cn-1an-1

cn-1bn-1=cn-1bn-1+cn-1an-1+cn-1bn-1

(an-1+bn-1)(bn-1+an-1)n-1=an-1+bn-1

(bn-1+an-1)(an-1+bn-1)n-1=bn-1+an-1

推出

因此

cn-1an-1=cn-1an-1+cn-1bn-1+cn-1an-1

cn-1bn-1+cn-1an-1+cn-1bn-1=cn-1bn-1

另外，有：

(an-1+cn-1)(bn-1+cn-1)n-1=

an-1+cn-1bn-1+an-1cn-1+cn-1

an-1+cn-1

类似地

因此

(an-1+cn-1)(bn-1+cn-1)=(an-1+cn-1)

类似地

(bn-1+cn-1)(an-1+cn-1)=(bn-1+cn-1)

因此

在上述推导过程中已经证明了

[1] BURRIS S,SANKAPPANAVAR H P.A Course in Universal Algebra[M].New York:Springer,1981.

[2] HOWIE J M.Fundamentals of Semigroup Theory[M].Oxford:Oxford Science Publication,1995.

[3] PETRICH M,REILLY N R.Completely Regular Semigroups[M].New York:Wiley,1999.

[4] ZHAO X Z,SHUM K P,GUO Y Q.L-subvarieties of the variety of idempotent semirings[J].Algebra Univers,2001,46:75-96.

(责任编辑 陈 艳)

On Semiring Varieties Related to Green’sL-Relations

WANG Li-li, WANG Li-qun

(College of Science, Chongqing University of Technology, Chongqing 400054, China)

semiring; variety; green’s relation

2017-04-25

重庆市教委科学技术研究项目(KJ1500925, KJ1600930)

王丽丽(1981—), 女, 山东泰安人, 博士,副教授,主要从事代数理论研究,E-mail: wllaf@cqut.edu.cn。

王丽丽,王立群.与格林L-关系相关的半环簇研究[J].重庆理工大学学报(自然科学)，2017(6):184-187.

format：WANG Li-li, WANG Li-qun.On Semiring Varieties Related to Green’sL-Relations[J].Journal of Chongqing University of Technology(Natural Science)，2017(6):184-187.

10.3969/j.issn.1674-8425(z).2017.06.028

O153.3

A

1674-8425(2017)06-0184-04