基于BP神经网络自动识别沉积微相方法

马 奎



基于BP神经网络自动识别沉积微相方法

马 奎

（中国石油勘探开发研究院，北京100083）

基于测井数据的深度挖掘性，提出了前馈式（BP）人工神经网络的沉积微相识别方法。在测井数据较少、井多的条件下深入挖掘有限的测井数据，得到具有沉积学意义的样本指标，对比不同沉积微相指标，找到各自特征。通过训练样本的优选，建立了训练样本集，对BP人工神经网络拓扑结构选择和网络训练方法进行分析和试验，总结了网络拓扑结构设置方法和成长型网络训练方法。实现了在测井数据不足、微相特征复杂的条件下实现了高效率、高准确度的沉积微相识别，其独特优势在石油地质研究中有着广泛的应用前景。

BP神经网络；沉积微相；测井数据；训练样本

在地质研究中分析沉积微相，目前采用的常规手段是通过建立单井解释模版，结合井位分布与亚相分布控制按照地质研究人员的经验进行判别。工作量大，操作复杂，不利于工作开展，且不同地质研究人员对工区地质特征认识有不同，判定结果也有出入。近年来，有学者开始采用其他方法进行沉积微相判别，具代表性的有：①靳松等利用不同沉积微相对应测井曲线段之间实测数据的变差函数（变程、主方向、次方向）特征差异进行微相判别[1]，将地质统计学算法中经典的变差函数[2]引入到沉积微相判别中，利用不同微相测井数据的数值变异特征进行判别。但是在实际应用中还是存在着操作难度大，识别特征不明显等问题；②唐为清等利用（多层前馈式）神经网络算法进行沉积微相判别[3-4]。通过不同微相的样本进行网络训练，训练完成之后将待分析样本投入到网络中去计算，即可得出判别结果，操作难度大为减小，判别正确率也很可观（在训练样本准备合理时可达90%[5]）。利用神经网络算法进行沉积微相判别实质上是应用BP神经网络的模式识别和非线性映射的能力，通过神经网络建立起样本参数与沉积微相的映射，来达到微相判别的目的。前馈式（BP）神经网络具有良好的非线性映射和容错能力，只要建立起合适的神经网络，即可进行高效的预测工作。是目前进行沉积微相判别的一种较为理想的算法。

目前也面临的问题：①样本数据的准备难度大。已进行的多种测井曲线的数值预测[6]，将储层的四性特征作为判断指标。但是在大多数油田，不同年代不同技术标准和仪器测得的数据差异性很大，不能一概而论，采用的分析指标也极其有限，所以在训练样本准备中存在一定的困难。②测井数据利用率不高。许少华等人在对测井数据进行样本化处理的时候采用了二值点阵法[4]。在处理过程中不得不遗漏部分测点数据，容易造成数据失真。③样本选取过程复杂。就神经网络而言，训练样本的多少直接关系到网络收敛速度，同类样本之间的差异性也影响收敛速度[7]。目前，样本数量巨大，怎样选取适量代表性样本是一个问题。④神经网络规模和拓扑结构难以确定，需要学习过程中进行优化[8]，有的学者将研究重点放在网络收敛速度上，而忽视了预测准确性的提高。

1 训练样本准备与测井数据深度挖掘

1.1 研究区状况

胜利油田坨七区块为三角洲相，主要亚相为三角洲前缘，发育的沉积微相有：水下分流河道、河口坝、河道间（也作泥岩）、前缘席状砂、远岸滩坝、近岸滩砂等沉积微相。各沉积微相特征复杂，单个样本特征不明显，测井数据偏少，主要有自然电位(SP)、自然伽马(Gr)、微梯度(ML1)、微电位(ML2)四种曲线，其他曲线较少，不能作为全局指标。另外，Gr曲线也有一定程度的缺失。区内共有井576口。对泥岩相统计其曲线特征，提取其不同测井数据文件中的SP、Gr、ML1均值和变异性（已归一化[10]）得到其分布特征。

由此可见，区内SP、Gr、ML1、ML2四种曲线应用最广，Gr在少部分井中缺失；其他测井数据则针对性强，总量太少，不能作为全区微相判别指标。根据现有资料，仅有Gr、SP、电阻率和含油性等资料是不足以训练满足要求的神经网络的。为了克服这个问题，需要对现有的测井曲线特征进行深入挖掘，提取更多的曲线特征和地质信息。与此同时，不同沉积微相的各项指标会有不同的组合特征，但在个体中表现不明显，图1中显示了个体之间的跳跃性和分段性特征，形成这个特征主要是因为从浅到深不同自然电位要发生基线偏移，且不同深度的储层有不同的岩性、物性特征。由不同测井数据文件中提取的数据列在图1中显示出跳跃性。若采用线性方法进行判别，需要进行复杂的数据处理，不仅难以得到适当的指标的系数，而且难以达到合格的准确率。

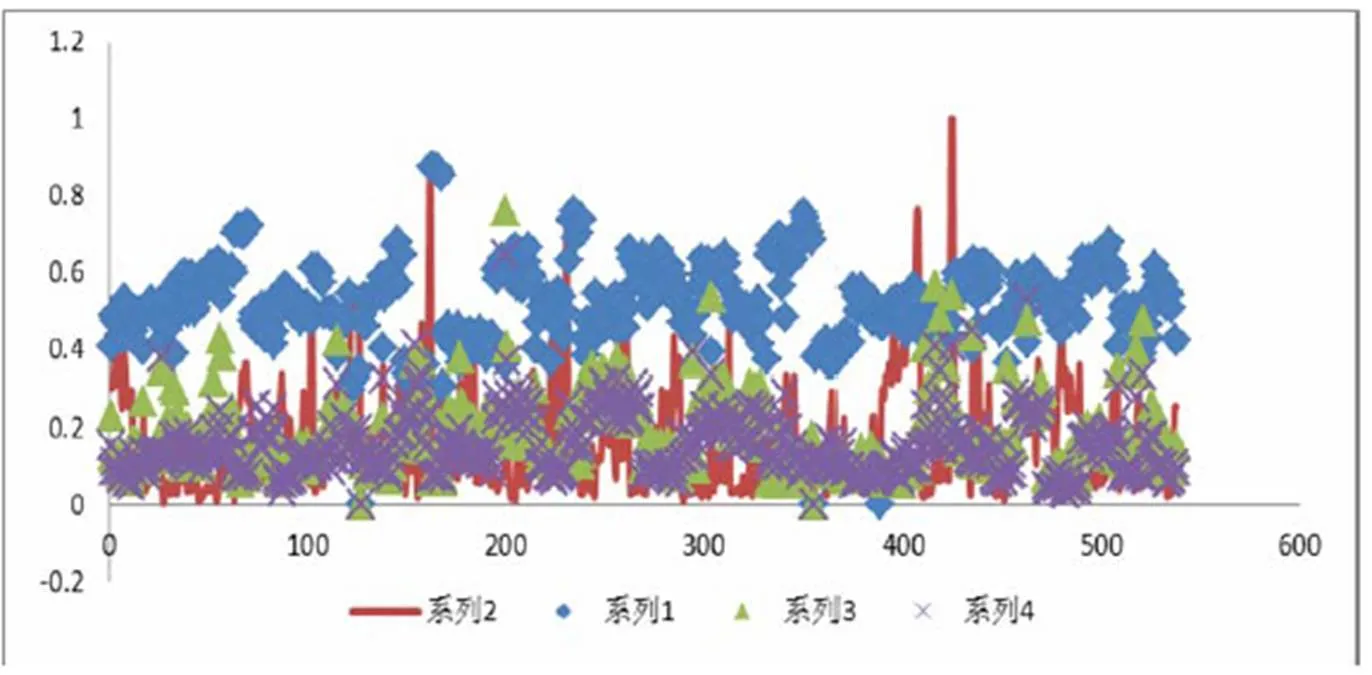
图1 泥岩相Gr(1)、SP(2)、ML1(3)、ML2(4)层段均值分布

图2 三种沉积微相自然样本SP-Gr均值交会图

因此，选定神经网络进行判别是一种优势方案，建立具有良好映射能力的神经网络需要有足够信息量和数量的训练样本群体。样本包含信息不足将导致映射关系模糊，过多的样本会影响网络的收敛速率。进行训练样本准备的时候需要对现有测井曲线资料进行深入挖掘，并合理选取适量有代表性的样本。

1.2 样本优选方法

基于不同沉积微相样本统计指标之间的差异性和单一样本指标的跳跃性，制定了综合性的样本优选方法，在去掉奇异值的前提下提取两类样本：统计型样本和单一自然样本。统计样本是将样本的主要指标进行统计，并按数值大小将样本分为低值、中间值、高值三个区间，对每个区间计算样本指标计算均值得到的指导性样本，在训练中加大其权重。单一自然样本则是根据样本的跳跃性特征，选取的不同特征的单一样本，在进行选取时主要考虑单一样本在样本总体中的广度和规律性。如图1中，不同层段的样本有不同的测井响应，选样过程中需要兼顾到隔层段的样本。

在完成样本选取之后对不同样本进行交会分析，比较各个指标，对出现冲突的训练样本进行再分析，修正冲突样本。在油田范围内，微相的各项指标在一定范围内浮动，选定较少的指标进行交会分析通常容易出现冲突。但是在多指标控制下，冲突大大减少。结合神经网络的非线性映射能力，能够进行高效合理的判别。

表1 测井曲线对应的样本指标

1.3 测井数据深度挖掘

前人研究中由于各种测井资料齐备，没有进行测井资料的深度挖掘，在本研究中，由于工区井数量大，测井资料较少，且多为原始数据，通过传统方式提取的数据有限，难以建立具有足够精度的映射关系的神经网络，需要进行测井数据的深度挖掘。从沉积学和统计学的角度出发，设计了曲线幅度均值、含油性、韵律指数、厚度系数等多个指标。

表1中各项指标：①变异系数：反映层内隔夹层出现频率，指示层内非均质性；②变差函数主方向：指示曲线形态特征[1]，采用混合编程方法[11]，将GSLIB程序库中的gam.f[12]程序整合到基于MFC的数据采集软件中去，一次性提取变差函数指标；③韵律指数：反映水体进退特征,选用SP较为平滑的曲线；④厚度系数：为单层厚度，每层厚度变化较大，在大量样本存在的情况下服从统计学特征，能够起到一定的约束作用。

以上共有9个可选指标，因此设置输入层为9个神经元。据此可定义一个9×1的矩阵作为神经网络输入模版。

2 神经网络拓扑结构的选定与网络训练

2.1 神经网络拓扑结构的选定

选定神经网络的拓扑结构进行是整个神经网络模型构建中最基本的一环，主要包括层次结构和单层神经元数量关系。所选样本的数量和复杂度一定程度上决定了所需神经网络的拓扑结构。前人在对神经网络的拓扑结构与其收敛速率上进行过初步的研究，认为3层（即只有一个隐含层）的神经网络即可适应沉积微相判别[13-15]。但是在实践中，特别是测井数据不足的情况下，这种简易、局限的网络设置方法并不能适应网络训练的需求。

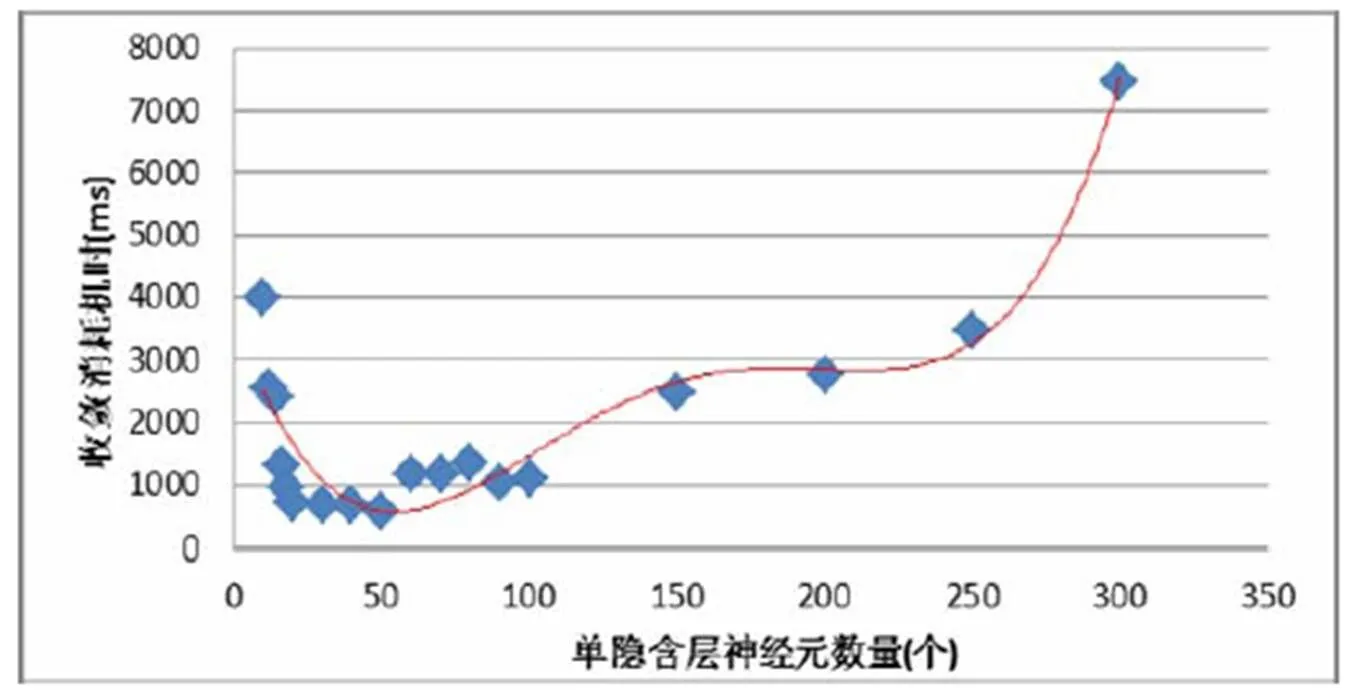
图3 三层神经网络拓扑结构与训练耗时对比

图4 四层神经网络拓扑结构与训练耗时对比

针对神经网络拓扑结构与其收敛性关系，选取阿拉伯数字0-9的点阵模式作为训练样本在不同神经网络拓扑结构下进行训练实验。样本大小为6×7，每个模式（数字）1个样本，误差精度设为0.000001。在训练过程中观测训练所需时间作为评价网络收敛效率的指标。整个测试分类两个阶段。

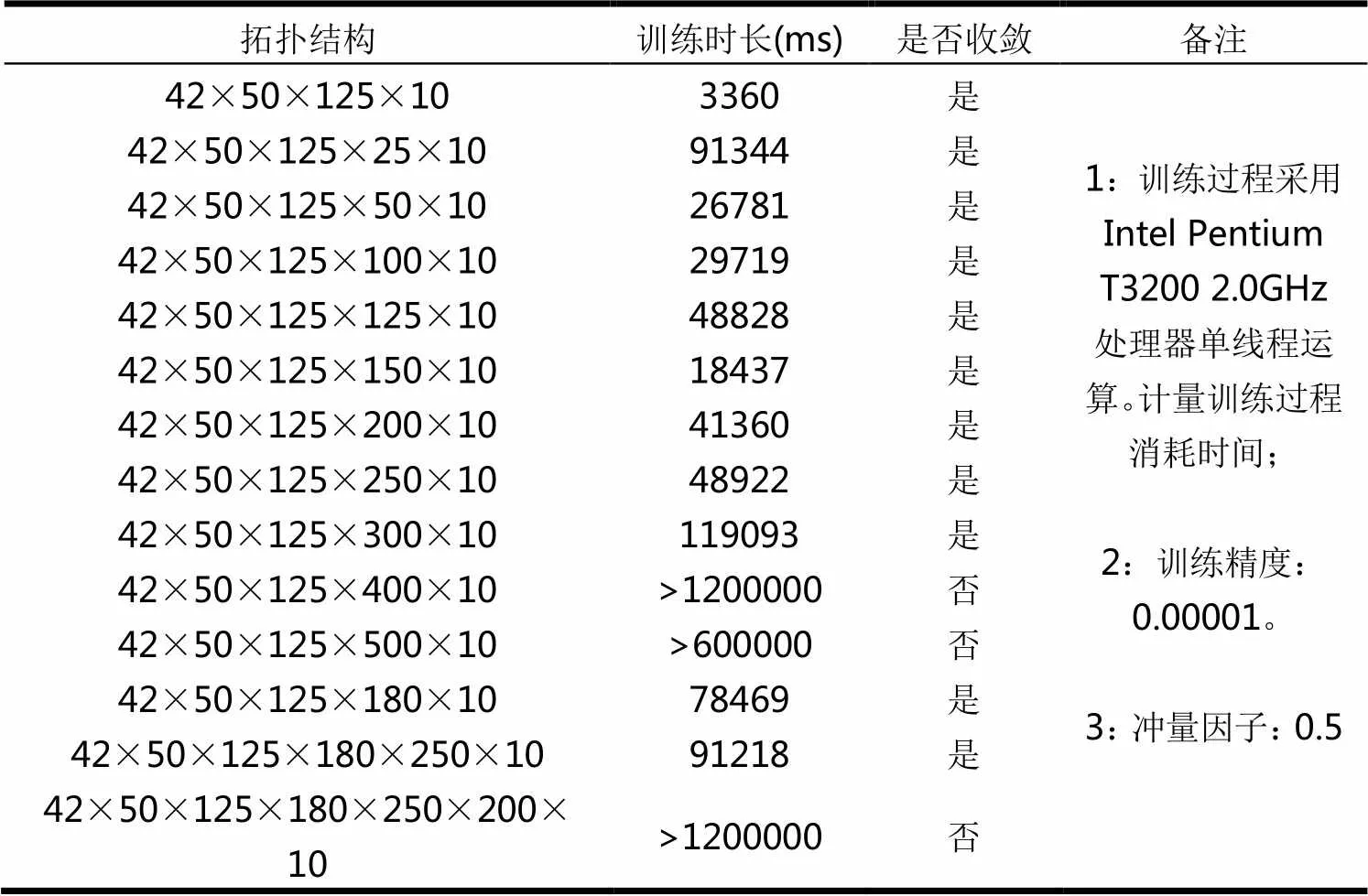
表2 多层神经网络拓扑结构与训练耗时

1）针对一个隐含层条件下，研究其神经元数目对收敛效率的影响。选取20个不同值进行实验，对结果进行回归分析。因此，在单隐含层的条件下，将隐含层神经元个数设置为输入层的0.4~6倍能够较快收敛，隐含层神经元数目过少将导致网络无法收敛，而过多则会导致整个网络复杂，无法在有限时间内达到收敛。

2）在多个隐含层下对神经网络收敛特性研究，重点对4~6层的神经网络进行对比实验。考虑①中实验结论，设置第二层（第一隐含层）神经元个数为50，对第二隐含层选取18个不同值实验，并对目标函数收敛速度回归分析。

因此，在多隐含层的条件下，随着隐含层增加，网络拓扑结构越来月复杂，网络训练过程中的正向传播和误差反馈过程计算量和调节力度都收到了限制，导致收敛时间逐步增加。隐含层数过多将导致训练时间过长或无法收敛等问题，使得其失去实用意义。

综上，对于神经网络的拓扑结构的设定，可以得出4点结论：

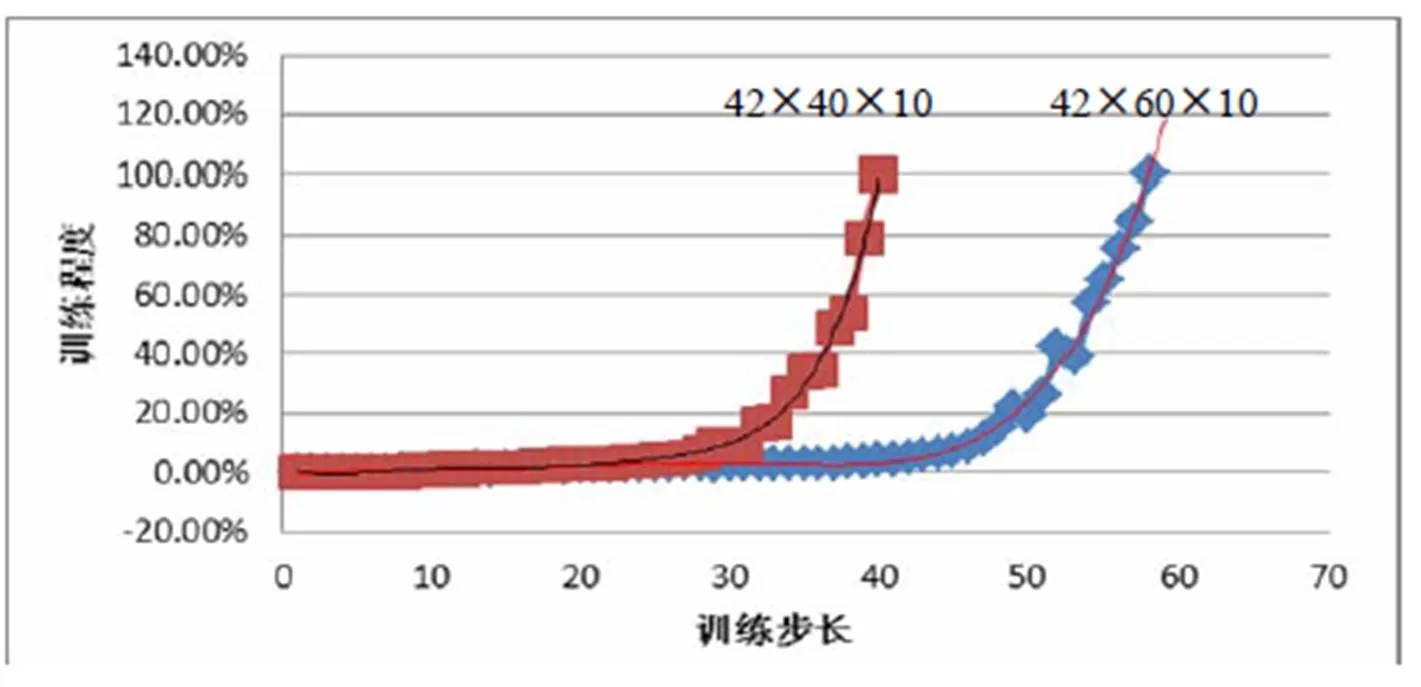
图5 两个三层神经网络的训练过程

1）在进行沉积微相识别等问题中，使用3-5层神经网络能够达到较好的训练速度和精度，追求过多的隐含层和复杂的神经网络结构会适得其反；

2）神经网络中，下层神经元数量是其上层神经元数量的0.4~6倍时，目标函数收敛速度较快，能够较快完成训练；

3）进行沉积微相识别等工作中，网络训练时间与网络的复杂度有直接关系，实际应用中，根据网络复杂度设定一个收敛时间限制，如5层以下的神经网络，训练超过15分钟未收敛则可能是网络拓扑结构不适合训练样本，需要中止训练并采用其他拓扑结构的神经网络进行训练；

4）网络训练时间长短不是重点，重点是找到能在有限时间内收敛的网络结构。多种网络结构进行多重预测能够提高预测确定性。

2.2 网络训练

2.2.1 网络训练的阶段性和冲量调整策略

进行网络训练的时候观察整个训练过程中发现，在前期，网络误差在90%以上的阶段往往需要消耗整个调整过程的90%以上的训练时间，在达到一定的精度之后网络收敛速度大大提高。图5是两个三层神经网络的收敛过程，按照一定的步长进行训练程度统计，得到其训练过程。

由图5可见，在网络训练初期，进行权值调整具有一定的混乱性，而在后期调整中，出现了一定的调节失误。这是由于在随机权值的基础上进行调节有一定的盲目性和试探性，如果冲量因子过小，会限制权重调节的区间；而在后期调节中，网络权值的调节幅度随着网络误差的减小而减小，如果冲量因子较大，就会出现过调节行为。为此，可以在调整初期增大权重调节的力度，适当增大冲量因子；而在网络误差达到80%以下之后适当减小冲量因子，以免出现较大的调整失误。

2.2.2 成长型神经网络

所谓成长型神经网络，就是在已经训练完成的神经网络的基础上通过强化训练和拓展训练不断拓展网络的映射能力。在样本总体发生改变，或者样本内部出现矛盾的情况下，之前的神经网络权值分布已经不能适应工作的需要，如果重新进行样本准备和网络训练将十分耗时，且有可能使网络目标函数难以收敛。考虑到之前的神经网络能够适应大部分样本，设计了成长型神经网络训练方法。主要分为以下三个方面：

1）对预测不准确，或者出现冲突的样本进行分析，除去样本集中的不良样本，将最新确认的样本群加入到样本集中，形成新的样本集，在原有网络权值的基础上进行网络迁移训练，纠正之前不良样本带来的影响；

2）对新增的样本类型（样本指标类型不变），为新增样本制定新的导师信号之后投入到之前的网络中进行拓展训练，强化网络的映射能力。

3）如果随着应用环境的变化，某些类型的样本退出了预测，则在进行网络判别时应当屏蔽退出样本对应的导师信号，退出模式识别过程。网络本身不需要进行演化训练。

3 实例研究

对胜利油田坨七区的各种沉积微相的测井曲线特征进行分析，按照上文方法提取个沉积微相各项指标统计数据，具体如表3。

表3 三种沉积微相曲线特征及指标统计

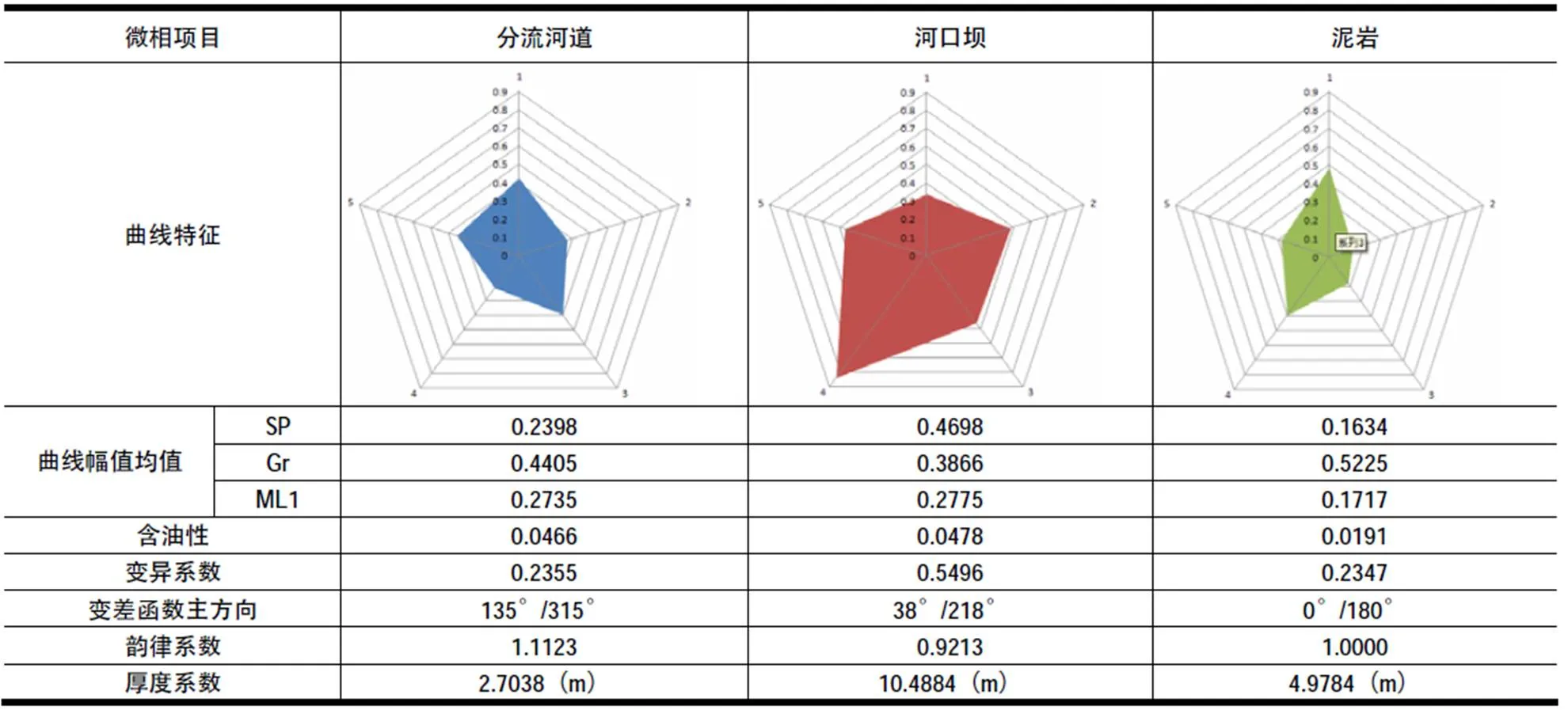
得到统计数据之后按照采集到的样本指标分布关系，选取足够的自然样本，形成自然样本群，最后将统计样本（基础样本）以一定的权重加入到样本群中去，形成样本集。

根据样本种类和样本指标，选定三种神经网络拓扑结构：A:9×15×7、B:9×15×20、C:9×15×20×30×7进行神经网络训练和识别。检验识别的标准有两个：对训练样本的识别准确率(C2)和对其他自然样本识别的准确率(C1)。由实际检验可得，对训练样本，判断的准确率为100%；对其他自然样本训练的综合准确率约为83%。在测井数据较少的条件下得到了良好的预测精度。

由于部分井缺少Gr数据，可将Gr相关指标设置为无视状态(在相应指标设置为“0”的条件下，各层神经元对此指标不进行计算)。通过实际识别检验，准确率为81%。不仅说明神经网络具有良好的容差能力，也证明训练样本选取具有很强的代表性。

4 结论与认识

从神经网络在沉积微相识别等领域的应用现状入手，对网络训练样本的选取、测井数据的深度挖掘、神经网络拓扑结构的优选与训练方法四个方面展开讨论，并用大规模的实际数据进行了实例研究。在测井数据不足、样本总量巨大、样本指标组合规律不明显的条件下得到了良好的沉积微相识别准确度。总体上取得了如下研究成果：

1） BP神经网络具有良好的非线性映射能力和容差能力，适合进行沉积微相一类的模式识别工作。通过编写应用程序，使得BP神经网络的应用更加便捷，在石油地质研究方面有很大的应用空间，如进行开发层系制定、流动单元预测；

表4 样本集构成与识别结果

2）在样本数据量大、包含信息量不足的条件下，进行测井数据的深度挖掘和沉积学分析对于提取更多样本指标、更好地表征沉积微相测井响应特征有积极意义而且势在必行；

3）神经网络的拓扑结构应当与输入层神经元（样本指标数）和样本复杂程度匹配，过于复杂和过于简单的神经网络结构都会给工作带来困难；

4）神经网络的拓扑结构与样本的匹配存在一定的随机性，按照神经元个数从上层到下层依次递增和增量约束的原则选取多种神经网络进行训练和识别是比较有效的方式；

5）学习型神经网络是一种有效的网络训练方法，是进行网络纠错和优化的有效手段。

虽然利用BP神经网络进行沉积微相识别具有可行性，但在识别准度上，特别是在样本数据较少的条件下，需要进一步提高识别的准确率；且前人进行模式识别时对输出层与各导师信号的对比和匹配较为简单，还应当考虑整个输出层的全局状态，以免判定过于片面；神经网络的拓扑结构选定范围尚不十分明确，需要进一步探究。在实际应用上，神经网络在地质研究中的应用范围不断扩大，研究深度也不断增大[16-20]，若在各种地质分析软件中集成神经网络模块，将能促进地质分析工作的智能化和高效化。

[1] 靳松, 朱筱敏, 钟大康. 变差函数在沉积微相自动识别中的应用[J]. 石油学报, 2006, 27(03):57~60 .

[2] Deutsch,C.V,Journal,A.G. GSLIB:geostatistical Software Library and User’s Guide .New York,NY: Oxford University Press, 1992, :340pp .

[3] 唐为清, 郭荣坤, 王忠东吗, 等. 沉积微相测井资料神经网络判别方法研究[J]. 沉积学报, 2001, 19(04) :581~585.

[4] 许少华, 刘扬, 梁久祯, 等. 基于遗传—BP算法和图像处理的沉积微相识别[J]. 石油学报, 2002,23 (03):48~51 .

[5] 许少华, 陈可为, 等. 基于遗传—BP算法和图像处理的沉积微相识别[J]. 大庆石油学院学报,2001,25(03):51~54..

[6] E.M. Iloghalu, “Application of Neural Networks Technique in Lithofacies Classifications used for 3-D Reservoir Geological Modelling and Exploration Studies.-A Novel Computer-Based Methodology for Depositional Environment Interpretation”, AAPG Annual Convention, Salt Lake.City,Utah, May 2003, 11-14.

[7] 杨斌, 匡立春, 孙中春, 等. 神经网络及其在石油测井中的应用[M]. 石油工业出版社, 2005.

[8] 张昭昭, 乔俊飞, 杨刚. 自适应前馈神经网络结构优化设计[J]. 智能系统学报, 2011,6(04):312~317.

[9] 王金荣, 刘洪涛. 测井沉积微相识别方法及应用[J]. 大庆石油学院学报, 2004, 28 (04): 18~20.

[10] 王楠. 测井曲线模式识别及其在地层对比中的应用[D]. 黑龙江大学硕士论文. 2008

[11] 李君, 李少华, 毛平, 等. VC++结合Fortran升级地质统计学算法[J]. 物探与化探,2009,33 (06):715~717.

[12] Carr J R, Miranda F P. The semivariogram in comparison to the co- occurrence matrix for classification of image texture .[C]IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(6) :1945-1952 .

[13] Funabashi K. On the approximate realization of continues mapping by neural networks.[J]Neural Networks,1989,2:183~192.

[14] Lippmann R P. Review of neural networks for speech recognition[J]Neural Computation, 1989,1:1~38.

[15] Cyberno G. Approximation by superpositions of a sigmoidal function. Mathematics of Control[J]Signals and Systems,1989,2(4):303~314.

[16] 孙鲁平,首皓, 赵晓龙, 等. 基于微电阻率扫描成像测井的沉积微相识别[J]. 测井技术, 2009,33(04): 379~383.

[17] 周金应, 桂碧雯, 李茂, 等. 基于岩控的人工神经网络在渗透率预测中的应用[J]. 石油学报, 2010,31(06):985~988 .

[18] K. Aminian, S. Ameri. Application of artificial neural networks for reservoir characterization with limited data[J] Journal of Petroleum Science and Engineering, 49 (2005) 212–222

[19] 宋延杰, 杨艳, 杨青山, 等. 过程神经网络在厚层细分水淹解释中的应用[J]. 测井技术, 2009,33(04) :340~344.

[20] Anna Ilce ´a Fischetti, Andre ´ Andrade.Porosity images from well logs[J] Journal of Petroleum Science and Engineering 36 (2002) 149– 158.

Automatic Sedimentary Microfacies Identification Method Based On BP Neural Networks

MA Kui

(Research Institute of Petroleum Exploration & Development, PetroChina, Beijing 100083)

This paper puts forward a method of sedimentary micro-facies identification based on logging data and BP neural network. Firstly, to take advantage of limited logging data in order to get sedimentological sample indexes, and to compare different micro-facies indexes to find their own features. Then training samples are optimized and sample set is established. Secondly, network topology and train growth-network are summarized based on analysis and experiment of network topology choice and training method. Finally, a experiment on net training and micro-facies identification by use of sample set and natural samples is conducted, which shows an accuracy ratio for 83% and realizes both high efficiency and precision of micro-facies identification.

BP neural network; identification; microfacies; logging data; artificial neural network; training data

P628+.3；P618.13

A

1006-0995(2017)02-0325-06

10.3969/j.issn.1006-0995.2017.02.036

2016-03-04

马奎（1988-），男，湖北黄冈人，在读博士，主要研究方向：油气藏形成与分布