几种常用GPS高程拟合模型对比分析

郝玉珠，罗竹，张俊



几种常用GPS高程拟合模型对比分析

郝玉珠，罗竹，张俊

（贵州大学矿业学院，贵阳 550025）

GPS高程拟合结果受研究区地形起伏、重力异常、数据质量、点位分布等复杂因素影响，很难有统通用的广泛适用性拟合模型。该文通过工程实例讨论了几种常用GPS高程拟合模型及其特点，得出有益结论。

高程异常；GPS高程拟合；平面拟合；对比分析

传统的几何水准测量虽然具有测量精度高、操作简单等优点，但是在测区距离长、范围大的情况下，通常需要花费大量的人力物力，因此效率较低[1]。为解决这一问题，许多测绘科技工作者研究利用高精度三角高程测量代替水准测量，取得了一定成果[2-4]。但三角高程测量依然是一种常规测量方法，野外作业效率提高不明显，且目前只有在十分严格的条件下才可以取代低等级水准测量。近年来，随着GPS技术在工程应用中的普及，越来越多学者开始研究利用GPS技术解决传统水准测量野外作业效率低下的问题[5~7]。解决这一问题的途径是采用一定的数学模型拟合给定区域范围的似大地水准面，当拟合模型确定后，即可利用一点的平面坐标计算出该点的正常高，这一技术被称为GPS高程拟合。GPS高程拟合关键是找到适合于研究区域的数学曲面模型，当给出的数学曲面与研究区域似大地水准面有最佳密合时，可以较高的精度满足工程实际需求。但是，由于影响高程拟合的因素非常复杂，这一技术需要通过在所研究得工程区域范围内进行数据采样，并通过实验来确定拟合模型。该文利用某地区实际工程测量数据，研究GPS高程的三种拟合模型，即平面、二次曲面和多面函数三种GPS高程拟合方法及其特点，通过对三种方法的对比研究，得出了一些结论，并给出利用这三种方法进行GPS高程拟合的建议。

1 三种高程系统及其关系

测量中，使用的高程系统根据定义的基准面和基准线不同，可分为三种。第一种是正高系统，这种高程系统以大地水准面为高程基准面，地面上任一点的正高系指该点沿垂线方向至大地水准面的距离；第二种是正常高系统，这种高程系统以似大地水准面为基准面，一点的正常高是指该点沿正常正常重力线到似大地水准面的距离，似大地水准面是由地面沿铅垂线向下量取正常高所得点形成的连续曲面，它不是真实的物理面，只是用以计算的辅助面；第三种是大地高高程系统，一点的大地高是该点沿法线方向至参考椭球面的距离。

以上三种高程系统在不同场合都有应用，我国规定在工程实际中，使用正常高系统。三种高程系统的关系如图1所示。

图1 三种高程系统

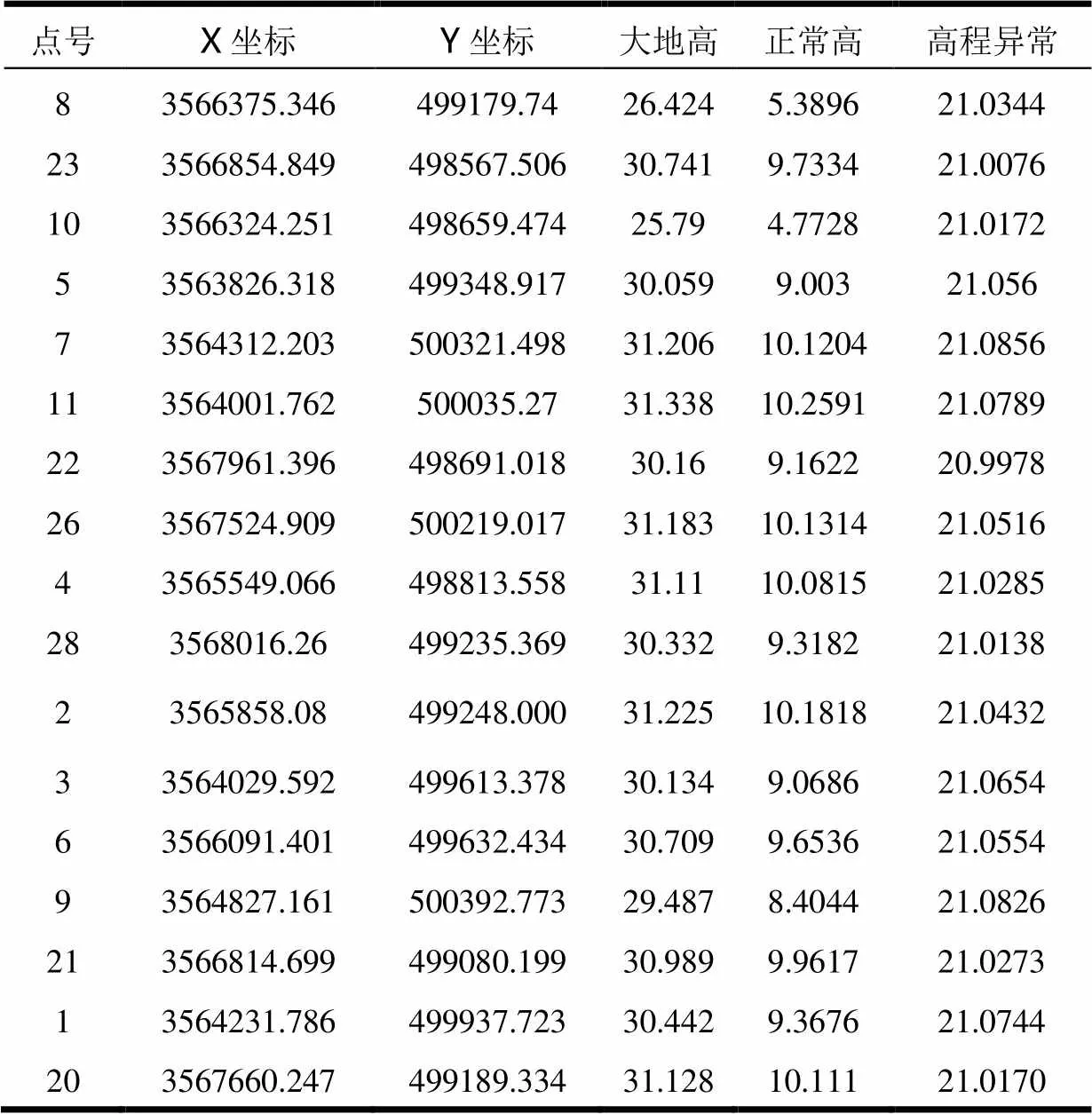
表1 已知数据表（单位：m）

由上图可知，大地高与正常高的关系为：（1）

2 三种常用的GPS高程拟合模型及其原理

实施GPS 高程拟合技术时，需要首先在工程区域若干控制点上同时进行GPS测量和水准测量，从而获取控制点上的大地高、平面坐标和正常高，根据这些点对应的大地高和正常高利用式（1）求出各点的高程异常值，当完成以上准备工作后，选择合适的数学拟合方法拟合出测区内的似大地水准面，确定拟合参数，最后利用点的平面坐标和拟合模型通过内插，计算出曲面上其它点的正常高。

2.1 平面拟合法

当测区范围很小且比较平坦时，可以近似地认为大地水准面趋于一个平面，高程异常已知点坐标满足如下表达式:

（2）

注意到，表达式中有aaa三个未知数，所以至少需要三个已知点，当已知点多于三个时，用最小二乘法求解[8]模型参数即可。

2.2 多项式曲面拟合法

多项式拟合的实质是构造一个多项式函数，使得该多项式函数所代表的曲面尽可能逼近高程异常的趋势曲。设测区内的任意一点的高程异常与平面坐标有如下关系：

（3）

式中，为高程异常的趋势面，为残差。由于高次多项式会带来震荡问题[9]，所以一般采用二次曲面拟合，即设：

式中6个未知数，故二次多项式至少需要6个已知点，即，当有多于6个的水准点联测时，则可以得到如下矩阵形式：

（5）

根据最小二乘准则求得向量的解，即AAAz后，由（4）式给出的二次曲面拟合模型即被确定。

2.3 多面函数拟合法

该方法理论基础为：任何表面,无论其是否规则,都能通过一定的方法构造出一个或多个规则的数学表面去逼近其表面[10]。这种方法实施原理为：在每个插值点上，同所有的已知数据点分别建立函数关系，并将这些多面函数的值叠加起来，以获得最佳的曲面拟合值。假设高程异常函数为：

式中，C为待定系数，为待定点坐标，xy为已知点坐标，xy为的二次核函数。一般情况下，可选取简单的对称的距离性的核函数，即

（7）

按最小二乘法原理，求得：

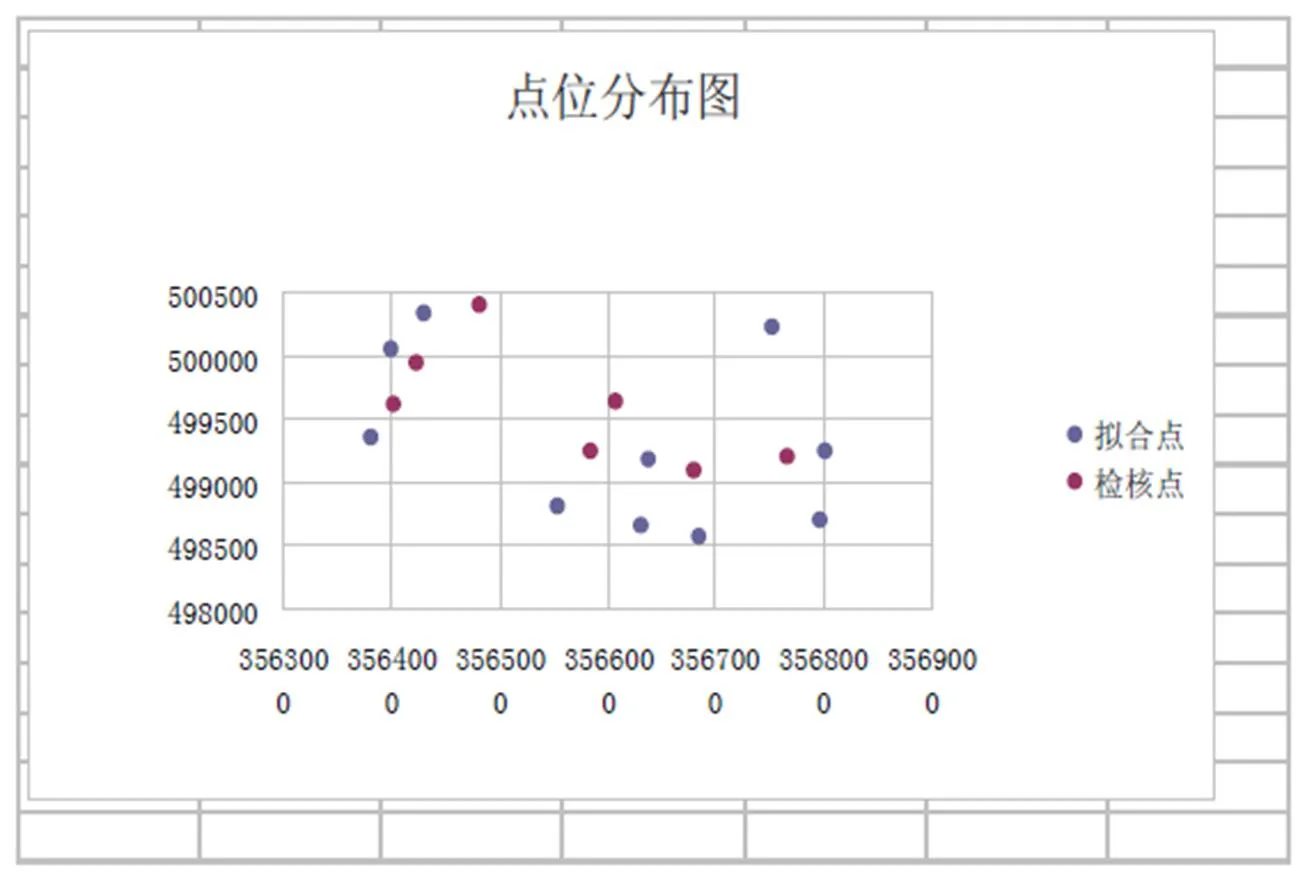
图2 点位分布图

3 算例及分析

使用文献[11]的数据进行计算，已知数据见表1。为直观，本文绘制了点位分布图，如图2所示，从图中可以看出，工程区域控制点分布较均匀，可满足GPS高程拟合要求。

将表1中17个控制点分为2组，并取10个点为模型的拟合点，后7个点作为检核点，具体分布如图2所示。为研究本区域不同GPS高程拟合效果，特采用以下三种拟合方案：

1）利用式（2）给出的平面拟合模型拟合研究区域的高程异常趋势面，并内插出检核点正常高。

表2 三种方案拟合残差

2） 利用式（4）给出的二次曲面拟合模型拟合研究区域的高程异常趋势面，并内插出检核点正常高。

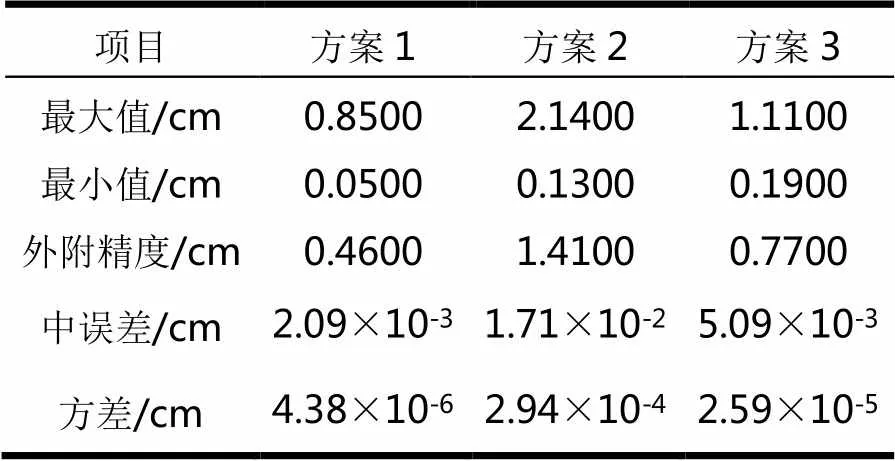
表3 三种方案拟合精度

3）利用式（7）给出的多面函数法拟合模型拟合研究区域的高程异常趋势面，并内插出检核点正常高。

三种方案拟合结果列于表2和表3，其中表2给出了三种拟合方案的拟合残差，表3统计了三种方案拟合残差的极值和外符合精度。

从表2中可以看出，除1号点外，三种方案整体上均达到了较好的拟合效果，绝大多数检核点拟合残差均达到了毫米级，但从表3精度统计情况看，方案1拟合精度明显高于方案2和方案3，其中方案2拟合效果相对最差。分析其原因，主要是因为本研究区域高程起伏不大，似大地水准面趋于缓和，平面模型能够较好的拟合本区域似大地水准面，而二次曲面由于模型本身数学特点，与平面属性相差较大，相对拟合效果不及平面模型。多面函数模型本质上也是利用多个非线性曲面拟合本区域似大地水准面，其拟合效果不佳原因也在于该地区高程异常趋势面客观上更接近于平面而非其他形式的复杂曲面。另一方面的原因还在于多面函数模型需要确定合适的平滑因子，但目前尚缺乏权威的理论解决这一问题，本文将平滑因子取为25 000，可能不是最佳的。

4 结束语

GPS高程拟合做为一种现代测绘技术，可以大大减少测绘工作者的野外劳动强度，提高工作效率，但是，这一技术的应用受到许多因素限制，必须根据实际工程区域的具体情况通过实验选择合适的拟合模型才可以满足工程要求。本文通过实际测量数据对比研究了三种常用GPS高程拟合模型在本测区的拟合效果，得出平面拟合模型为最佳模型。证明了在不同区域不同自然条件下对应的最佳模型可能是不同的，应根据工程区域实际慎重选择拟合模型。

[1] 姚涛, 兰孝奇, 马亮亮. GPS高程拟合模型及其应用研究[J]. 测绘与空间地理信息, 2015(3):147-149.

[2] 周水渠. 精密三角高程测量代替二等水准测量的尝试[J]. 测绘信息与工程,1999(3):25-29.

[3] 柏文锋, 熊斯, 黄利军, 陈远. 精密三角高程测量系统的研究与实现[J]. 科技资讯,2010(9):8-9.

[4] 段恩新. 复杂测区条件下精密三角高程测量技术的研究[J].石家庄铁道大学学报(自然科学版),2012(3):98-102.

[5] 邓罡.. GPS高程拟合代替水准测量研究[D]. 中南大学, 2012.DOI:10.7666/d.y2195611.

[6] 胡良柏. GPS高程拟合的研究[D]. 江西理工大学, 2009.

[7] 郝海亮. GPS水准代替三等水准测量技术应用研究[J]. 科技与企业, 2015(6):91-92.

[8] 伍青云. GPS高程拟合的方式及可靠性分析[J]. 中国煤田地质, 2006(3):70-72.

[9] 徐元海, 闻洪峰, 甄登春. GPS高程拟合方法比较[J].地理空间信息,2012(3):105-107.

[10] 焦殿阳, 张旭晴. 曲面拟合模型在小区域GPS高程拟合中的应用[J].测绘与空间地理信息,2012(3):24-26.

[11] 卢辉, 刘长星. MATLAB在GPS高程拟合中的应用[J].测绘科学,2009(2):191-193.

Comparison of Several Common GPS Elevation Fitting Models

HAO Yu-zhu LUO Zhu ZHANG Jun

(Mining College, Guizhou University, Guiyang 550025)

GPS elevation fitting results are easy to be affected by many factors such as topographic relief, gravity anomaly, data quality, measuring point distribution, and so on.As a result, it is difficult to find a model which can be used in any place for GPS height fitting. This paper has a discussion on three GPS elevation fitting models and their characteristics.

elevation anomaly; GPS elevation fitting; plane fitting; quadric surface fitting; polyhedral function fitting

P628+.3

A

1006-0995（2017）02-0335-04

10.3969/j.issn.1006-0995.2017.02.038

2016-06-26

贵州大学“大学生创新创业训练计划”项目：“GPS高程拟合方法及其在测量中的应用研究”，项目编号：贵大校创字2014（040）；贵州省教学内容与教学体系改革重点项目：“基于工程教育专业认证标准体系的测绘工程专业课程体系调整与优化（SJJG201413）”贵州大学教育教学改革项目：“三学期之下测绘工程专业课程设置优化方案研究（JG2013045）”

郝玉珠（1992- ），男，甘肃庆阳人，贵州大学测绘工程本科生在读