基于C#和Mat1ab混合编程遗传算法的平原区水闸优化设计

马 超

(河北省水利水电第二勘测设计研究院，河北石家庄050021)

基于C#和Mat1ab混合编程遗传算法的平原区水闸优化设计

马 超

(河北省水利水电第二勘测设计研究院，河北石家庄050021)

以某平原区水闸为例，采用遗传算法对水闸进行优化研究。以水闸工程造价最小为目标，以过流总净宽、闸墩厚度、闸室长度、闸门位置、闸底板厚度与铺盖长度为设计变量，以水闸几何尺寸为几何约束，以稳定安全系数、基底大小应力比及防渗长度作为性态约束，建立了水闸的数学优化模型，并介绍了遗传算法、C#和Mat1ab混合编程遗传算法的原理。通过优化水闸布置，减少了工程造价。计算结果表明该优化设计方法可以提高设计效率，是合理可行的。

水闸；遗传算法；优化设计；工程造价；C#和Mat1ab混合编程

水闸是一种利用闸门挡水和泄水的多建于河道、渠系及水库的低水头水工建筑物。水闸在水利工程中的应用十分广泛，但许多水闸的设计依旧停留在经验设计阶段，存在不经济、不合理等许多问题，所以水闸设计的合理性和经济性就成为亟待解决的问题，进行水闸优化设计十分必要。

1 优化设计数学模型

水闸设计很复杂，数学模型的建立需要对设计过程进行必要简化［5］，最终选取水闸过流总净宽、闸墩厚度、闸室段长度、闸门位置、闸底板厚度与铺盖长度作为优化变量。

1.1 目标函数

以工程造价为目标函数，设第i种材料的单位综合造价为Ci，在设计中所占的体积为Vi，则目标函数可表示为：

1.2 约束条件

(1)几何约束：x1≤xi≤xu，xi为变量的下限；xu为变量的上限。

(2)性态约束：①闸室稳定安全系数：Fs≥②基底大小应力比：③防渗长度：L≥CΔH。

1.3 最终优化的数学模型

设计变量在满足给定的约束条件的情况下，求得目标函数最小。

2 设计方法

2.1 遗传算法

遗传算法首先用随机方式产生一个初始群体，群体中的每一个个体称为染色体，对应优化问题中变量空间中的一个点；组成染色体的元素称为一个基因，对应优化问题中的设计变量。染色体的适应度反映可能解的优劣，根据优胜劣汰的原则进行选择，适应度大的被选择的机会大，通过连续遗传操作不断产生新的群体，经过若干代进化以后，就可能生成最佳个体。

基于对自然界中生物遗传与进化机制的模仿，Go1dberg［6］总结出了一种统一的最基本的遗传算法——基本遗传算法(Simp1e GeneticA1gorithms，简称SGA)。其遗传进化操作过程简单，容易理解，是各种遗传算法的基本框架，可不依赖于问题的领域和种类，具有一定的应用价值。

2.2 C#与MATLAB混合编程

C#与MATLAB混合编程采用动态链接库技术实现C#对MATLAB函数的调用。动态链接库是由MATLAB的Dep1oyment Too1将编写好的m文件或m脚本文件编译成动态链接库，C#通过调用动态链接库中的函数来完成与MATLAB的参数调用。

2.2.1 MATLAB创建动态链接库（DLL）

在MATLAB中根据向导新建Dep1oyment工程后把已经编写好的m函数添加进去进行编译，生成DLL文件即可被C#引用。具体步骤如下：

(1)按照遗传算法的计算原理，根据需要编写创建动态链接库时所需的文件，遗传算法主函数文件(ycsf.m)、目标函数文件(mbhs.m)和约束条件函数文件(ystj.m)。其中ycsf.m文件主要代码如下：

(2)创建DLL。在MATLAB中创建DLL工程，编译完成之后在上面输入的存储位置下即可找到创建完成的ycsf.d11文件。

2.2.2 C#调用DLL

首先我们应该把上述生成的DLL引入计算程序才能调用。引入后在使用之前实例化该DLL类，具体如下：

2.2.3 数据类型转换

完成C#对ycsf.d11的引用之后，如何实现将计算参数从C#传递到MATLAB，并且如何将MATLAB的计算结果返回给C#，并通过C#把计算结果展示出来，就成了C#与MATLAB混合编程的关键。由于C#与MATLAB的数据类型不同，所以为实现2者之间数据类型的相互转换，主要要用到MATLAB提供的MWA rray接口。因此，还需要添加对MWArray的引用，并在C#的头文件中添加。

(1)C#数据向MATLAB数据转换。若是数据类型不需要转换，如是数组类型则通过MWArray转换。如：MWNumericArray A1=A，其中A为C#中的doub1e型数组，经过赋值之后A被转换为MATLAB中的doub1e型数组A1。

(2)MATLAB数据向C#数据转换。

访问resu1t数组中的元素时还需要做相应的强制类型转换。转换如下：

上句转换中0表示resu1t数组的第一个元素，访问resu1t［0］中的某一元素时可用out_Arr［i］表示，代码如下：

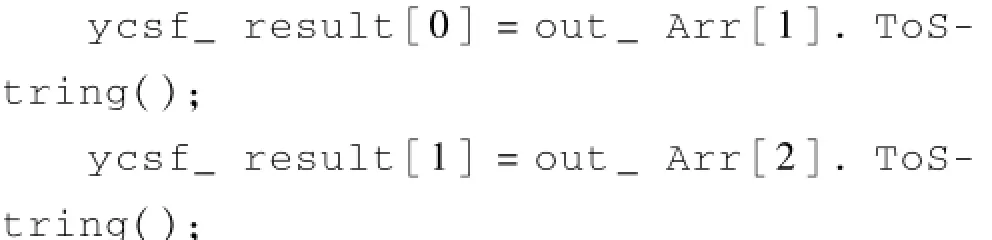
2.3 C#与M ATLAB混合编程的其他方法

因为MATLAB提供了C#可以直接调用的接口文件，所以C#与MATLAB混合编程除采用上述方法外，还可以采用C#直接调用MATLAB可执行文件进行计算。

对2种方法的计算结果进行了对比，发现结果一致，只与输入的参数有关系。在本优化算法中采用前述方法进行优化设计。

3 工程算例

3.1 工程概况

某干渠位于武邑县城南约6.3km，其中某水闸位于清凉江侧江河干渠渠首，设计流量45m3/s，闸下设计水位17.731m。上游设计挡水位为10年一遇洪水位17.88m。

3.2 基本资料

(1)综合比价：闸室：闸墩：铺盖：挡土墙= 900∶800∶700∶900。

(2)几何约束：①总净宽≤x1≤建闸宽度；②0.9≤x2≤1.5；③2.0ΔH≤x3≤3.5ΔH；④0.2≤x4≤0.8；⑤0.7≤x5≤2.0；⑥3.0ΔH≤x6≤5.0ΔH，ΔH为上下游水位差。

(3)性态约束为：①稳定安全系数不小于1.3；②基底大小应力比不小于1.5；③防渗长度不小于CΔH。

3.3 优化结果

经过遗传算法初拟计算后得到的优化结果见表1。

表1 优化前后结果

4 结论

本文计算中采用的Mat1ab是一个功能强大的计算工具，利用C#和Mat1ab混合编程遗传算法效果好，结果准确，对于优化设计提供了新思路，对其他水利工程的优化设计具有一定的实际应用和推广价值。优化设计前后工程造价相差23.5%，表明水闸优化设计十分必要。由于水闸设计本身十分复杂，所以本优化算法进行了适当的简化，但用于水闸的初拟设计、初拟布置是可行的，具有很好的参考价值。

［1］王海娟，辛全才，马红娜.基于MATLAB的覆盖层地基上混凝土面板堆石坝断面优化设计［J］.水资源与水工程学报，2009，20(05)：120-122.

［2］平巍巍，赵艳.基于改进遗传算法的混凝土面板堆石坝优化设计［J］.电网与水力发电进展，2008，24(01)：64-67.

［3］钱令希.工程结构优化设计［M］.北京：中国水利电力出版社，1983：1-9.

［4］蔡新，郭兴文，张旭明.工程结构优化设计［M］.北京：中国水利水电出版社，2003：191-207.

［5］周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999：4-64.

［6］王小平，曹立明.遗传算法—理论、应用与软件实现［M］.西安：西安交通大学出版社，2002：1-122.

［7］钱治航.混合离散优化算法及工程应用研究［D］.华中理工大学，1993.

［8］刘浩，韩晶.MATLAB R2014a完全自学一本通［M］.北京：电子工业出版社，2015.

［9］赵忠海，张洪文，刘秀峰.基于C#与MATLAB混合编程实现变形预测分析［J］.测绘与空间地理信息，2012，35(05)：122-124.

［10］姚光强，陈立平.基于COM技术的C#与Mat1ab混合编程［J］.计算机工程，2008，34(14)：87-89.

TV66

B

1672-2469(2017)03-0083-03

DO I：10.3969/j.issn.1672-2469.2017.03.030

2017-01-17

马 超(1984年—)，男，工程师。