镶嵌正方格子上铁磁Ising模型的相变

尹训昌

(安庆师范大学,安徽 安庆 246011)



镶嵌正方格子上铁磁Ising模型的相变

尹训昌

(安庆师范大学,安徽 安庆 246011)

应用等效变换的方法，把镶嵌正方格子铁磁Ising模型转化为可求解的正方格子。采用重整化群变换，得到了正方格子上Ising模型的临界点。通过得到的两个变换关系，求得镶嵌正方晶格上Ising模型的临界点为K*=0.405。

相变；Ising模型；重整化群

0 引言

相变是自然界中广泛存在着的一种现象，它是凝聚态物理范围中的一个研究热点。1944年，Onsager通过数学推导得到了二维正方晶格上Ising模型的严格解[1]，此后相变的研究一直得到人们的重视[2-7]。Ising模型是一种最简单的自旋模型，它的自旋只能取±1两个值，可以模拟自然界中铁磁材料的相变，研究Ising模型的相变具有重要的现实意义。本文研究的镶嵌正方格子是典型的平移对称晶格，与典型的正方晶格相比较，更加贴近自然界中的真实系统。研究利用等效变换和键移重整化群的方法，讨论镶嵌正方格子上Ising模型的相变。

在正方晶格上，在每个顶点上各放置一个自旋，再把一个自旋放在每个边长的中点上，把中点的自旋格点连接起来，通过恰当的排列就形成了镶嵌正方格子，如图1所示。

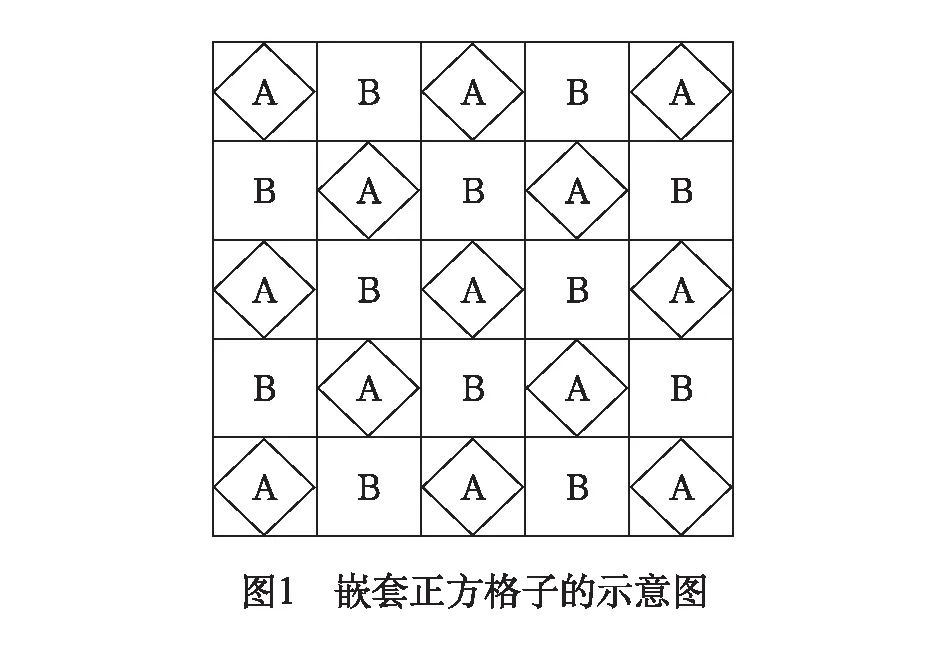
分析可知，该格子可以分成单元A和单元B两个部分。为了简便，在单元A中我们假设只有近邻相互作用，则此部分上Ising模型的有效哈密顿量为

(1)

其中，K表示约化的近邻相互作用参数，它只能取±1两个值。本文所研究的是K>0的铁磁Ising系统。

1 等效变换过程

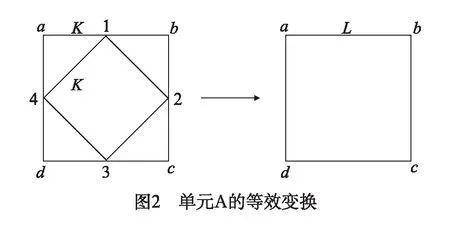
图2表示等效变换的过程。单元A等效变换前的近邻相互作用用K表示，L表示变换后的近邻相互作用。由表达式(1)，可以得到单元A的哈密顿量

HA=H1+H2

(2)

其中

H1=K(sas1+sbs1+sbs2+scs2+scs3+sds3+sds4+sas4),

H2=K(s1s2+s2s3+s3s4+s4s1),

应用等效变换，约去内部中点上的4个自旋si(i=1,2,3,4)，此过程表示为

(3)

上式中Q是一个积分常数，等效变换后的哈密顿量用H′表示。

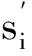
(4)

其中

(5)

(5)式为等效变换关系。

通过等效变换过程，单元A系统转化为熟知的可以求解的正方形格子。分析得知，单元B也相应地转化成正方形格子，本文所研究的铁磁Ising系统就变成正方形格子上的铁磁Ising模型的相变问题。

2 正方形格子上的铁磁Ising模型

正方格子上铁磁Ising模型重整化群过程如图3所示。令相互作用参数和键一起移动，用键移动的数目形象地描述相互作用的大小，即相互作用参数与键的数目成正比。分析可知，图3(Ⅰ)通过键的移动后变成图3(Ⅱ)，它的哈密顿量的表达式为

H=3L(sas1+s1s2+s2sb)

(6)

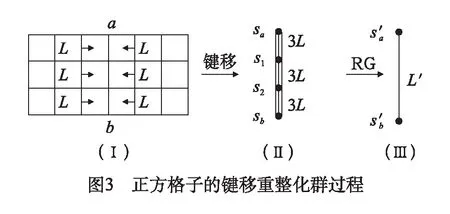
消去内部格点自旋变量后图3(Ⅱ)变为图3(Ⅲ)，系统的哈密顿量为

(7)

采用与上面相同的方法，可以得出重整化群的递推关系为

(8)

由递推关系(8)，得正方格子上铁磁Ising模型模型的相变点为

L*=0.2406

(9)

3 结论

应用上面的结果，把表达式(9)代入式(5)，得到了镶嵌正方格子上铁磁Ising模型，模型的相应点为K*=0.405。先通过等效变换方法，把本文所讨论的系统变成正方格子系统，然后应用格点消约重整化群得到正方格子上铁磁Ising系统的递推关系，通过两个递推关系，得到讨论系统的相变点。由结果知，本文所研究系统的相变点和单纯的正方格子的Ising系统有明显的不同。

[1] Onsager L.Crystal statistics.I.A two-dimensional model with an order disorder transition[J].Phys.Rev.,1944,(65):117-149.

[2] Gefen Y,Mandelbrot B,Aharony A.Critical phenomena on fractal lattices[J].Phys.Rev.Lett.,1980,(45):855-858.

[3] Li S,Yang Z R.Real-space renormalization-group study of the phase transition in a Gaussian model of fractals[J].Phys.Rev.E,1997,55(6):6656-6660.

[4] Kong X M,Lin Z Q,Zhu J Y.Critical behavior of the Gaussian model on fractal lattices in external magnetic field[J].Sci.China A,2000,43(7):767-779.

[5] 孙春峰.钻石分形晶格上Ising模型的配分函数与关联函数[J].物理学报,2005,54(8):3768-3773.

[6] 尹训昌,刘万芳,祝祖送,等.Sierpinski地毯上S4模型的临界特性[J].物理学报,2015,64(1):235-239.

[7] 尹训昌,刘万芳,赵玉杰,等.嵌套正方格子上反铁磁高斯模型的相变[J].原子与分子物理学报,2016,(1):153-155.

The Phase Transition of Ferromagnet Ising Modelon Square Decorated Lattice

YINXun-chang

(AnqingNormalUniversity,Anqing246011,China)

Using the equivalent transformation technique, the ferromagnet Ising model on square decorated lattice is translated into the solvable square lattice. Then according to the renormalization group (RG), it deduces the critical pointK*=0.405 of Ising model on square lattice. Combining two recursion relations obtained in this paper, the critical point of Ising model on square decorated lattice is given.

phase transition; Ising model; renormalization-group

2017-01-08

安徽省自然科学基金(AQKJ2014B019)

尹训昌(1979-),男,硕士,安庆师范大学物理与电气工程学院副教授，研究方向：凝聚态物理。

O414.13

A

1674-3229(2017)02-0023-02