测量软件坐标系的建立和应用

袁 婷，刘 晟，刘雅君

(西安理工大学，陕西 西安 710082)



测量软件坐标系的建立和应用

袁 婷，刘 晟，刘雅君

(西安理工大学，陕西 西安 710082)

在测量软件中，坐标系的建立是后续测量和评价的基础。从坐标系建立原理出发，深入讨论了测量行业应用坐标系的理论方法，分析了测量行业的坐标系转换模型，并建立了矩阵理论模型，给出了矩阵理论公式。首先，按照测量软件功能对不同环境下的坐标系进行分类，深入分析不同类型坐标系的应用方法；其次，论述了不同坐标系的关系，按此分类搭建起软件合理的坐标系系统；最后，以模型坐标系为例，给出了坐标系数据的两种不同应用方式，以及不同方式产生数据的具体处理办法。按照所述原理和方法，可快速、高效地搭建测量软件的坐标系处理系统，对搭建类似CAD系统软件的坐标系模块有积极的借鉴作用。

测量软件；坐标系；模型坐标系；坐标系转换

0 引言

坐标测量系统是用来完成工件的测量、计算、评价的。而测量、计算、评价之前的必要条件就是统一基准，基准的统一是通过坐标系的统一来完成的。简单来说，测量、计算、评价之前，必须先参考设计图纸确定理论坐标系；然后依据理论坐标系，用实际元素测量值，建立实测坐标系。当理论坐标系和实测坐标系统一之后，坐标测量系统才能根据设计图纸的要求进行后续的测量、计算、评价工作。

在现代测量软件中，随着CAD技术的引入，通过CAD系统可快速实现理论数据的读取、测量结果画图、测量过程的仿真、测量结果的对比、脱机编程等相关功能。对测量软件而言，坐标系统不再是理论坐标系和实测坐标系的二元关系，它已经演化为理论坐标系、实测坐标、模型坐标系、虚拟机器坐标系等坐标系的之间的多元关系。

本文将探讨测量软件中坐标系建立的原理和方法，以及在CAD系统中各种不同坐标系的使用方法和相互关系。

1 坐标系建立的原理和转换方法

1.1 坐标系建立的原理

在测量软件中，通常存在实际定义的机器坐标系统，它是根据实际机器硬件使用情况定义的，如机器的原点、三维方向的定义。而在进行工件测量时，则需要在工件的坐标系下进行测量和评定。这时就需要把机器坐标系和工件坐标系进行统一。

测量软件通过采集工件上的点位信息，计算与之对应的基本几何元素。坐标系的建立，就是根据工程图纸提供的基准信息，测量摆放在测量机上工件的相对应位置，计算出作为基准的几何元素，再通过元素的几何信息(位置信息和方向信息)，利用几何关系找到坐标系间的坐标定位和变换关系进行数学计算，从而建立起要使用的工件坐标系统，这一过程通常称之为坐标系找正。

坐标系找正通常要经过三步操作完成：

(1)根据测量基准定义，确定空间轴的矢量方向。它实际对应的是测量工件的基准平面或者基准轴。通常可以用作此基准的几何矢量包括平面的法矢量、圆柱的轴矢量、圆锥的轴矢量、直线的矢量。

(2)确定平面轴的矢量方向。这个矢量方向是垂直于第一轴的平面上的一个轴方向。若实际基准元素的方向与空间轴不垂直，则平面轴的方向是基准轴线或基准平面法向在垂直于空间轴的平面上投影的方向[1]。通常可以用作此基准的几何矢量有平面的法矢量、圆柱的轴矢量、圆锥的轴矢量、直线的矢量。

(3)确定坐标系原点。它是测量工件的基准位置。通常可以用点的位置、圆的圆心位置、球心位置、圆柱和圆锥的顶点作为坐标系的原点。

1.2 坐标系的转换方法

测量软件通常使用三种坐标系类型：直角坐标系、圆柱坐标系、球形坐标系。直角坐标系统是通过线性变换矩阵实现坐标变换的，一般用它作为坐标系变换的基础[1]。

测量软件涉及的坐标系变换一般包括两种类型：坐标系平移和坐标系旋转。进行坐标系转换时可以先平移后旋转，也可先旋转后平移。采用齐次坐标技术来描述空间的各点坐标及其变换，即采用一个4×4矩阵描述[2]。按照右手定则变换。

测量软件经常使用的坐标系转换模型如下。

(1)平移矩阵的转换模型

若空间平移量为(Xt,Yt,Zt)，则平移变换为：

(2)绕坐标轴旋转矩阵的转换模型[3]

绕X轴旋转：

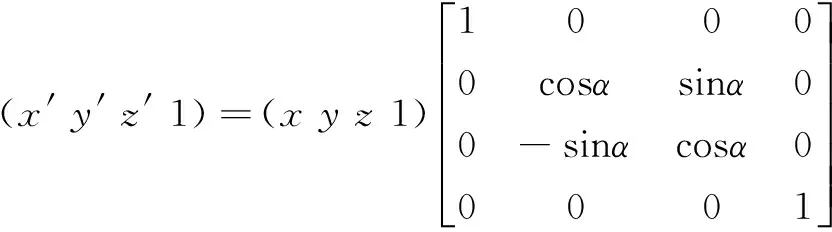
绕Y轴旋转：

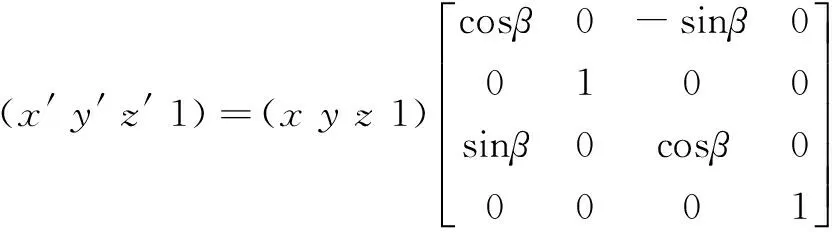
绕Z轴旋转：

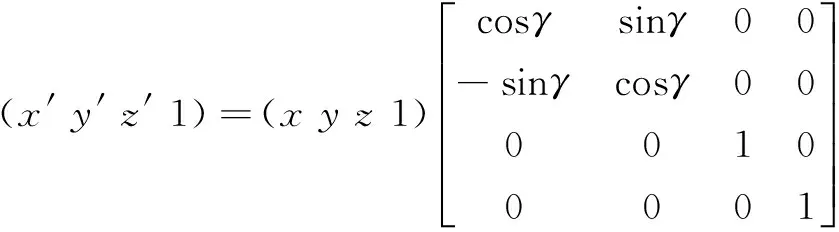
(3)绕任意空间轴旋转矩阵的转换模型

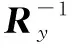
2 坐标系的分类和相互关系

2.1 坐标系的分类

根据测量软件的坐标系使用的不同场景，把坐标系细分为实测坐标系、理论坐标系、模型坐标系和虚拟机器坐标系，它们是各自模块功能和模块数据处理的基础。

(1)实测坐标系

在实际测量机器中，坐标机存在光栅、计数系统，机器根据零位、计数方向定义了初始的坐标系统，这个在现实环境中定义的坐标系称为机器坐标系用Org表示[4]。

依据实际测量操作，在工作台上放置测量工件，根据设计图纸或CAD模型的坐标系定义(理论坐标系用Nom表示)，用测量机测量的几何实测值(Org坐标系下)建立实测坐标系(工件坐标系)用Act表示。当实测坐标系和理论坐标系匹配在一起以后，就可以根据设计图纸要求进行测量、计算以及评定等工作。

(2)理论坐标系

理论坐标系是设计人员定义的理论基准，测量人员根据设计图纸或CAD模型确定理论坐标系，然后依据理论坐标系建立与之匹配的实测坐标系。对测量、计算以及评定工作而言，只与实测坐标系、理论坐标系相关。

(3)模型坐标系

模型坐标系是CAD模型导入后，CAD模型自带的坐标系。如果模型坐标系和理论坐标系重合，则不需要考虑模型坐标系，如果模型坐标系和理论坐标系不重合，就需要使用模型坐标系转换功能，转换模型坐标系到需要基准上。

(4)虚拟机器坐标系

CAD中的机器模型需要与实际机器、CAD模型建立对应的坐标变换关系，所以引入了虚拟机器坐标系。它主要用来完成虚拟机器的显示和虚拟运动控制。

2.2 坐标系的相互关系

(1)实测坐标系是机器坐标系参照理论坐标系建立起来的，它是测量软件的核心坐标系；实测坐标系与模型坐标系没有直接关系；实测坐标系建立起来后，虚拟坐标系也需要进行相应的变换，以实现真实机器与虚拟机器的同步。

(2)理论坐标系是由设计图纸的基准确定的，它是测量、评定的基础，它是实测坐标系建立的参照基准；理论坐标系可由模型坐标系转换而来；理论坐标系与虚拟坐标系没有直接关系。

(3)模型坐标系是模型进行坐标系变换时记录的坐标系，模型坐标系是依据理论坐标系的位置关系进行模型转换的。模型坐标系进行转换后，虚拟坐标系也需要进行相应的变换，以确保虚拟机器与模型相对位置的对应关系。

(4)虚拟机器坐标系是应用于CAD机器模型的，它反映了CAD机器模型相对实测坐标系和模型坐标系的相对变换关系，正确实现CAD机器模型的虚拟运动功能。

3 坐标系的应用方式

坐标系的应用方式是指如何把坐标系应用到实际功能模块中。根据数据不同的应用方式可将其分为两种，即数据变换方式和坐标系变换方式[5]。以模型坐标系为例，说明两种方式的不同使用情况，对于其他坐标系而言，可根据不同的使用场景使用相应的变换方式实现。

3.1 模型坐标系变换方式

CAD中模型坐标系变换有两种方式，一是把转换矩阵直接应用到几何实体中，原有的模型坐标系不变，这种方式叫动模型，效果如图1所示；另一种是把转换矩阵生成一个新的坐标系，CAD进行操作时需要把数据转换到这个坐标系下进行，这种方式叫动坐标系，效果如图2所示。

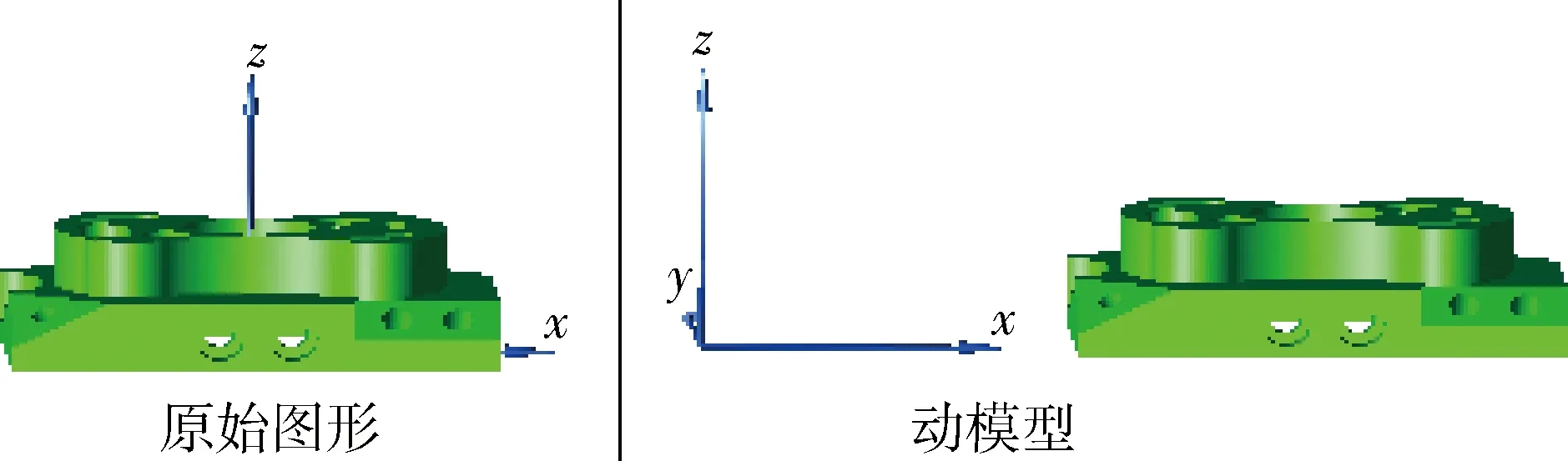
图1 动模型效果

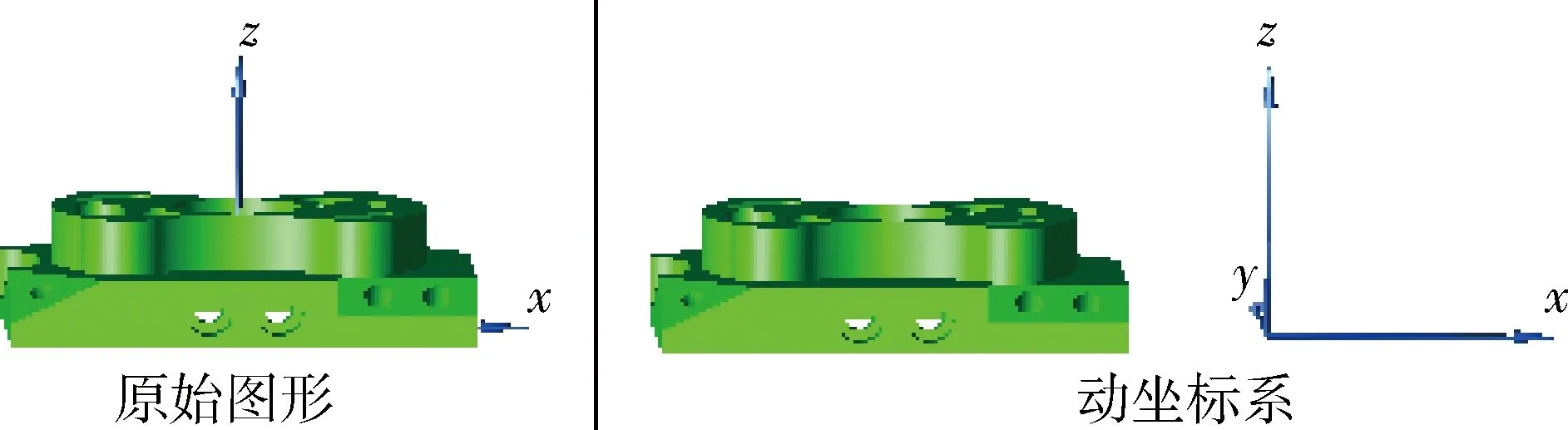
图2 动坐标系效果

上述两种模型坐标系变换方式各有优缺点。

(1)动模型

优点：转换数据直接应用到几何实体中，后续不需要进行模型坐标系转换操作。

缺点：模型坐标系变换时，效率比较差、数据处理量大，每次变换模型坐标系时都要进行“矩阵应用到每一个实体，模型实体重新刷新”。如果模型文件比较大，则会影响软件的执行效率。

(2)动坐标系

优点：只建立转换的模型坐标系，效率高，模型转换时数据处理量可忽略不计(与动模型)，模型坐标系转换与模型大小无关。

缺点：后续的CAD操作需要进行模型坐标系转换工作。

3.2 不同变换方式的数据处理

选择动模型方式，因为把转换矩阵直接应用的几何实体上，模型默认矩阵不变，所以不需要后续转换操作。

选择动坐标系方式，因为只是建立了新的模型坐标系，后续的操作数据与模型数据就需要通过新的模型坐标系转换实现它们在CAD视图界面显示的统一。

转换模型数据是通过在新建立的模型坐标系编写一对转换函数来实现的，这里把由默认模型坐标系转换到新的模型坐标系称之为正转换，把由新的模型坐标系转换到默认模型坐标系称之为反转换[6]。

几何数据可以分为三类：位置数据、矢量数据、标量数据。需要处理的数据是位置数据和矢量数据，它们都需要编写各自的一对转换函数。例如圆，圆心是位置数据，圆法矢量和主轴矢量是矢量数据，而圆的直径、半径是标量，不需要转换(任何坐标系下值不变)。

正转换和反转换是根据新的模型矩阵进行的，一个是利用新的模型矩阵进行变换，另一个是利用新的模型矩阵的逆阵进行变换的[7]。

转换模型数据对实际操作而言包含了两种转换操作，在拾取模型数据时，取到的值需要转换到建立的模型坐标系下，这是因为模型转换矩阵没有应用到模型上的几何实体中，CAD视图没有重新刷新，拾取操作的拾取值还是转换前的数据；外部数据的输入又需要通过建立的模型坐标系反转换，实现CAD视图数据与CAD模型数据的统一，这是因为测量的理论基准是以转换后的模型坐标系建立的，但模型数据没有变，要使画图和模型重合在一起，测量数据需要反转换。是否转换模型数据的画图效果比较如图3所示。

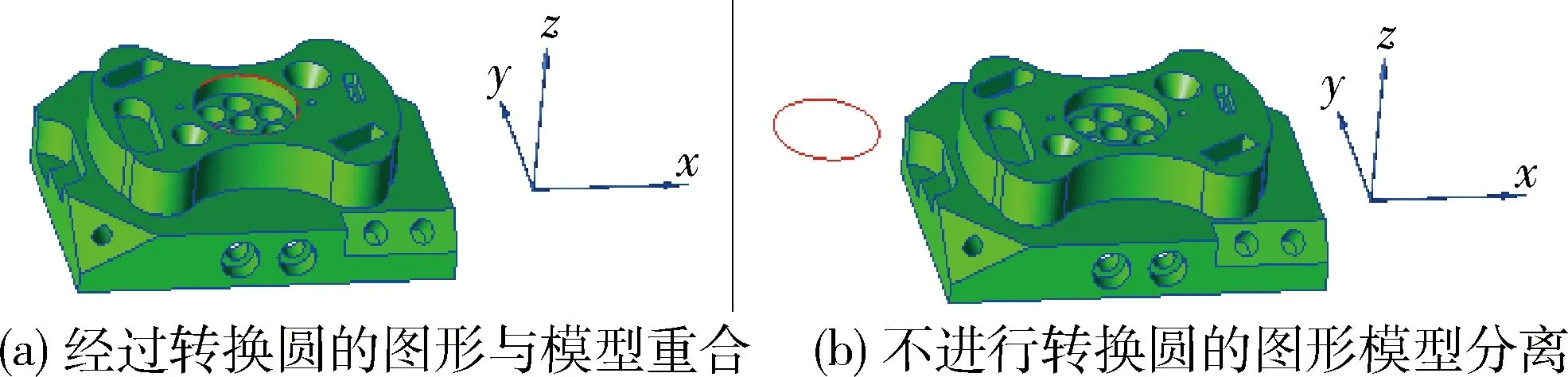
图3 是否转换模型数据的画图效果比较

4 结论

测量软件坐标系的建立和应用是从坐标系建立原理出发，本文探讨了软件系统中需要建立的坐标系统，分析了不同坐标系的相互关系，简述不同坐标系变换方法的优缺点，并给出具体的数据处理方法。本文介绍的原理和方法可以在实际测量软件中进行应用，它能准确、高效处理不同功能模块的坐标系变换关系。

[1] 王亚平,郑彦龙.三维测量软件系统中的坐标系的建立方法[J].工业计量，2004，14(6): 27-30.

[2] 闫志刚.图形学中绕任意轴旋转矩阵的推广[J].计算机时代，2009(12): 65-66.

[3] 柯金朴. 空间三维坐标转换原理及实现[J].江西测绘,2008(3):34-37.

[4] 游文霞,常俊晓,苏良虎.矩阵对策专用软件系统设计与实现研究[J].微型机与应用，2015，34(14):21-23.

[5] 卢波,丁峥时,张鹏.工程工业测量系统软件中坐标系的建立方法[J].建筑工程技术与设计，2013(9):40-44.

[6] 刘念,邹湘军,叶敏,等.复杂环境下的多工件定位研究[J].电子技术应,2015,41(12):120-128.

[7] 陈祖明.矩阵论引论[M].北京：北京航空航天大学出版社，1998.

The establishment and application of measuring software system of coordinates

Yuan Ting, Liu Sheng, Liu Yajun

(Xi’an University of Technology, Xi’an 710082, China)

In measuring software, the establishment of coordinate system is the foundation of the successive measurement and evaluation. Based on the principle of coordinate system, the theory and the method of measuring coordinate system in industrial application are deeply discussed in this paper. We make a deep analysis on the coordinate transformation model in measuring, and present a formula of matrix theory. In this paper, firstly, the coordinate systems in different settings are classified according to the functions of the measuring software, comparing the application methods of different kinds of coordinate system. Then the relationship in the different coordinate systems is discussed, and the reasonable coordinate system is built based on the classification. Finally, taking the model coordinate system as an example, the two different applications of the coordinate data are presented, as well as the corresponding specific data processing method it generates. In accordance with the principle and method proposed in this paper, a coordinate measuring software processing system could be quickly and efficiently built. It could be used for a reference for the development of other analogous CAD system.

measuring software; coordinate system; model coordinate system; coordinate system transformation

TP311

A

10.19358/j.issn.1674- 7720.2017.12.024

袁婷，刘晟，刘雅君.测量软件坐标系的建立和应用[J].微型机与应用，2017,36(12)：80-83.

2016-12-20)

袁婷(1977-)，女，硕士，讲师，主要研究方向：计算机软件及应用。

刘晟(1980-)，女，博士，讲师，主要研究方向：计算机图形学 。

刘雅君(1985-)，女，硕士，讲师，主要研究方向：模式识别。