基于进离场容量转化的航班延误优化研究
罗小林
(中国民航西北地区空中交通管理局 飞行服务中心,陕西 西安 710082)
基于进离场容量转化的航班延误优化研究
罗小林
(中国民航西北地区空中交通管理局 飞行服务中心,陕西 西安 710082)
为了提高机场运行效率,缓解航班延误,研究了进离场容量转化的特性,并建立了以延误时间最小的航班优化模型。结合实际运行数据对模型进行了验证,探讨了进场航班权重系数对进离场容量转化的影响。结果表明:采用进离场容量转化的方式可以增加进离场总容量,从而降低航班运行的总延误;该模型能提供优化的流量分配方案,可应用于机场流量管理。
空中交通管理;进离场容量;航班延误;动态规划
0 引言
随着国民经济的快速增长,人们对于航空运输的需求不断增大。但在实际运行过程中,机场成了空中交通运输的短板,伴随机场容量限制产生的交通阻塞、航班延误等问题越来越严重,迫切需要提升航班的保障工作。因此,对航班延误进行深层次研究,运用科学合理的方法尽可能减缓与控制延误,不仅是空中交通流量管理的重要内容,也是关系国计民生的焦点问题。
目前一些学者针对机场地面等待策略的研究取得了丰硕的成果[1-5],然而他们的研究主要集中于进场航班对机场容量的影响,很少考虑进离场容量之间的转化关系;另一些学者以减少延误成本为目标[6-10],对产生延误后的航班运行具有很强的参考价值,然而对延误的规避鲜有涉及。
鉴于此,本文在研究进离场容量的基础上,结合航班延误产生的原因与特性,考虑它们之间的相互关系,构建航班延误优化模型,然后以此模型对繁忙机场高峰时段进行优化,并对结果分析讨论。
1 进离场容量相互转化过程分析
机场容量并不是一个恒定值,受到空域结构、跑道使用方式、运行机型的类别以及天气情况、管制员的工作状态等因素的影响。一般来说,跑道单元是制约机场容量的瓶颈单元。目前国内绝大多数机场的跑道同时用于进场与离场,进场和离场这两个过程使得机场容量始终是动态变化的。在给定的条件下,对每一种进离场混合方式,有一个容量对:进场容量和相应的离场容量。它们的关系可通过进场-离场容量曲线来表示[5,8]。
如图1所示,顶点C表示机场最大离场容量D和相应的最小进场容量,顶点B则表示机场最大进场容量A和相应的最小离场容量。从顶点B到顶点C之间的线段表示进场和离场容量相互转化的区域。在此区域内,进场容量的增加可通过减少离场容量为代价并且取代其减少的部分,反之亦然。因此,在实际航班运行过程中,可通过灵活分配进离场容量来平衡高峰进离场航班的需求。
就某一繁忙机场而言,一般存在四种情形:(1)进场航班量大,甚至出现盘旋等待的情况,并且离场航班量大,地面等待延误现象严重,此情形通常发生于午后,进离场航班需求都很大;(2)进场航班量大,离场航班量小,此情形通常发生于晚上,进场航班需求大,离场航班需求较小;(3)进场航班量小,离场航班量大,此情形通常发生于清晨,进场航班需求小,离场航班需求大;(4)进场航班量小,离场航班量小,此情形通常发生于深夜,进离场航班需求都较小。对于各运行保障单位来说,合理地进行流量调控实现延误的最小化,不仅有利于飞行安全,也能更好地保证经济效益。
2 机场航班延误优化模型建立
2.1 航班延误的类别
《航班正常管理规定》(交通运输部令2016年第56号)中将航班延误分为:航班到港延误、航班出港延误和机上延误,并对其含义做了明确的说明[11]。
航班到港延误是指航班实际到港挡轮挡时间晚于计划到港时间超过15分钟的情况;航班出港延误是指航班实际出港撤轮挡时间晚于计划出港时间超过15分钟的情况;机上延误是指航班飞机关舱门后至起飞前或者降落后至开舱门前,旅客在航空器内等待超过机场规定的地面滑行时间的情况。
为便于研究,本文依据航班延误发生的位置划分为航班空中延误与航班地面延误。从实际运行来看,离场航班在地面排队等待远比进场航班在空中盘旋安全得多。
2.2 航班延误优化模型构造
将机场在时间区间[0,T]等分为N个时间段,设Arr0为前一段时间区间剩余的进场排队序列,Dep0为前一段时间区间剩余的离场排队序列,则第n+1个时间段之初的进离场队列可表述为:
Arrn+1=max(0,(Arrn+Rn-Vn)),n∈N
(1)
当n=0时,Arr1=Arr0,式中Arrn表示第n个时间段之初机场的进场队列,Rn表示第n个时间段内机场的进场需求,Vn表示第n个时间段内机场的进场容量。
Depn+1=max(0,(Depn+Dn-Cn)),n∈N
(2)
当n=0时,Dep1=Dep0,式中Depn表示第n个时间段之初机场的离场队列,Dn表示第n个时间段内机场的离场需求,Cn表示第n个时间段内机场的离场容量。
公式(1)(2)表示每一个时间段内进、离场队列的变化情况,第n+1个时间段之初的队列等于第n个时间段内的队列先加上交通需求,再减去该条件下的机场容量;若此值小于零,则取值为零。该时间区间航班保障延误最小、流量最大,可表述为此时间区间内各时间段累积的航班队列最小,即:
(3)
公式(3)中,αn∈[0,1],表示进场航班的权重系数。当αn>0.5时,航班空中延误较少;当αn<0.5时,航班地面延误较少。通常情况下,αn应大于0.5,减少航班空中延误,降低安全保障风险。
设arrn为第n个时间段进场航班的数量,depn为第n个时间段离场航班的数量,有:
arrn≤Vn,n∈N
(4)
depn≤Cn,n∈N
(5)
同时,第n个时间段内航班的进离场数量,不高于机场在该时段内的起降容量标准,即:
arrn+depn≤Ln,n∈N
(6)
还有小部分进、离场需求,不能延误,需要在预计的时间进行航班保障工作,如军用航班、重要飞行等,它们在模型的求解过程中具有较高的优先级。
3 模型求解与结果分析
根据美国数学家R.Bellman等人提出的“最优化原理”:“一个过程的最优决策具有这样的性质,即无论其初始状态和初始决策如何,其今后诸策略对以第一个决策所形成的状态作为初始状态的过程而言,必须构成最优策略”[12]。简言之,一个最优策略的子策略,对于它的初态和终态而言也必是最优的。其数学描述为:为了解决某一优化问题,需要作出n个决策,即D1,D2,…,Dn,如果这个决策系列是最优的,则对于任何一个整数k,1 最优化原理是动态规划的基础。任何一个问题,如果失去了这个最优化原理的支持,就不可能用动态规划方法计算。能采用动态规划求解的问题都需要满足一定的条件:(1) 问题中的状态必须满足最优化原理;(2) 问题中的状态必须满足无后效性。无后效性是指:下一时刻的状态只与当前状态有关,而和当前状态之前的状态无关,当前的状态是对以往决策的总结。 3.1 模型求解 本文构造的机场航班延误优化模型完全符合动态规划的条件,因此采用动态规划方法进行求解,其每个时间段内的求解流程如图2所示。 (1)首先从各保障单位获取航班运行信息,这些信息包括:时间段n内进、离场容量对数据;所有用户的进离场需求;各航班的任务性质,进而确定航班的优先级;实时获取空中交通管理部门、机场与航空公司的调整信息。 (2)若时间段n内初始进、离场交通需求与前一时间段留下来的进、离场航班队列在容量范围内,即该时间段流量小于容量,此时有较多的航班策略可供选择,且无论选择哪一种策略,均不会为下一时间段留下进、离场队列,则只需安排一种保证不留有任何队列的策略作为该时间段内航班运行的策略,不进行优化。 (3)若该时间段n内初始进离场交通需求与前一时间段内留下来的进、离场航班队列超出了容量的范围,即该时间段流量大于容量,则求得使αnArrn+1+(1-αn)Depn+1最小的进、离场容量值,以此优化进、离场率,进而分配航班时隙。 (4)对步骤3得到的航班序列进行延误信息分析,若能接受,则不必进行容量转化再优化,算法结束;若不可接受,则调整进场航班权重系数αn,返回步骤3再次优化求解。 (5)重复步骤(2)-(4),得到时间区间[0,T]内经过延误优化的机场航班序列。 3.2 实际运行数据分析 2016年西安咸阳国际机场客流量居全国第八,近期航班起降量日均约为850架次,航班运行形势与压力十分严峻。机场有2条跑道,跑道配置为:05L/23R,05R/23L。本文数据来源于2017年2月某天的进离港航班数据,当天跑道运行方式为:05跑道混合运行,即跑道05L与05R可同时用于进场和离场。根据机场的状况与限制信息,获得进离场容量对配置数据,得到基于15分钟的西安咸阳国际机场在各种进离场航班比例下的进离场容量曲线图(见图3)。 当天10-12点之间进离场交通需求(架次),如图4所示。 当天由于雨雪天气,能见度较差,在此时间段内进、离场需求分别达到了103与75架次,航班保障形势十分严峻。使用基于进离场容量转化的机场航班延误优化模型,不同α值,延误航班架次如表1所示。 表1 进离场容量控制与延误信息表 由表1可以得出:采用进离场容量转化的方式可以增加进离场总容量,从而降低航班运行的总延误。固定容量进离场的运行模式下,10-12时的总容量为88架次,采用进离场容量转化模式下,α=0.3时,该时间段容量为90(约增加了2.03%);α=0.4时,该时间段容量为104(约增加了18.18%);α=0.5时,该时间段容量为104(约增加了18.18%);α=0.6时,该时间段容量为97(约增加了10.23%);α=0.7时,该时间段容量为96(约增加了9.09%)。α值的选择对于容量转化具有十分重要的影响。从容量转化的效果上来看,α=0.3时,该时间段的进场容量为70,离场容量最小(为20);而当α=0.7时,进场容量为24,离场容量最大(达到72),进、离场容量值变化剧烈。 建立的航班延误优化模型考虑了进离场容量的转化对航班的影响,能够用于降低航班运行的总延误。针对不同α值的延误优化分析,当设置α=0.5时,进、离场容量分配较为均衡合理,能在贴近客观实际的前提下较好地提高优化策略的可执行性。 实际运行中,机场、航空公司和空管部门,应当建立协同交互的机制,实时共享航班状态信息,以确定合适的α值。本模型中只考虑了航班延误的时间成本,航班延误造成的经济损失、顾客服务和后勤保障成本等因素,是值得进一步研究的内容。 [1] ODONI A R.The flow management problem in air traffic control[M].Berlin:Springer-Verlag,1987:269-288. [2] HOFFMAN R,HALLW,BALL M.Collaborative decision making in air traffic flow management[M].Berkeley:UCBerkeley,1999:22-27. [3] PULUGURTHA SS,NAMBISAN SS.Using genetic algorithms to evaluate aircraft ground holding policy under static conditions[J].Journal of Transportation Engineering,2001,127(5):433-441. [4] 赵秀丽,朱金福,郭梅.不正常航班延误调度模型及算法[J].系统工程理论与实践,2008,28(4):129-134. [5] 田勇,董云龙.基于进离场容量转化的航班地面等待程序[J]. 系统工程理论与实践,2008,28(9):172-176. [6] 徐肖豪,李雄.航班地面等待模型中的延误成本分析与仿真[J].南京航空航天大学学报,2006,38(1):115-120. [7] 夏正洪,康瑞,周广军,等.延误航班地面等待成本计算模型[J].四川大学学报(自然科学版),2015, 52(4):793-799. [8] 田勇,吴东晖,万莉莉,等.基于突发事件的机场进离场时隙分配研究[J].武汉理工大学学报(信息与管理工程版),2016,38(1):28-32. [9] 张玉州,程玉胜,张步忠,等.航班地面等待问题建模及优化[J].中国科学技术大学学报,2011,41(2):149-156. [10] 严俊,吴桐水,高强,等.协同决策机制下的时隙二次指派[J].南京航空航天大学学报,2013,45(1):140-146. [11] 中华人民共和国交通运输部.航班正常管理规定(交通运输部令2016年第56号)[EB/OL].(2016-05-20)[2017-04-15].http://zizhan.mot.gov.cn/zfxxgk/bnssj/zcfgs/201607/t20160721_2065610.html. [12] 钱颂迪,甘应爱,田丰,等.运筹学:本科版[M].4版.北京: 清华大学出版社,2005:190-203. [责任编辑、校对:周 千] Study of Optimizing Airport Flight Delays Based on Arrival-departure Capacity Conversion LUOXiao-lin (Flight Service Center,Northwest Regional Air Traffic Management Bureau of Civil Aviation of China,Xi′an 710082, China) Based on arrival-departure capacity conversion,the paper studies the model with the minimum delay to promote airport operation efficiency and reduce flight delays,verifies the model with the actual operation data,and analyzes and discusses the approach flight weight coefficient′s impact on conversion of arrival-departure capacity.The results show that:the total capacity can be increased for reducing flight delays by adopting the mutual conversion between arrival and departure capacity.This method can provide optimal flow allocation schemes,and is suitable for airport traffic management. air traffic management;arrival-departure capacity;flight delay;dynamic programming 2017-04-06 中国民用航空局科技项目(MHRD20130213) 罗小林(1987-),男,四川广元人,助理工程师,主要从事空中交通管理研究。 V355 A 1008-9233(2017)03-0073-05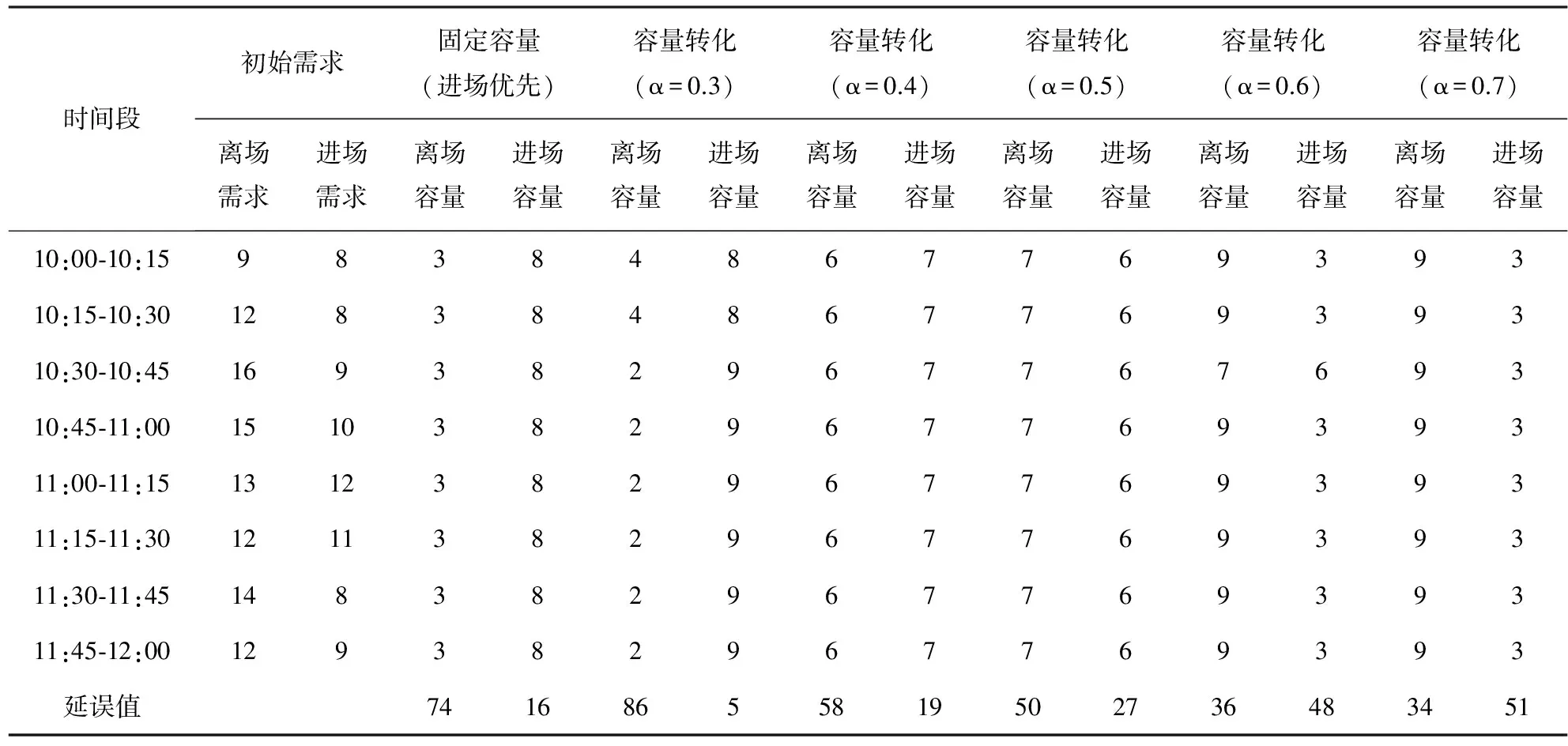
4 结语

