基于具有加权模糊隶属函数的神经网络的混沌时间序列预测

权鹏宇，车文刚，周志元，龙 婧

(1. 昆明理工大学 信息工程与自动化学院，云南 昆明 650500；2. 昆明理工大学 云南省计算机技术应用重点实验室，云南 昆明 650500)

基于具有加权模糊隶属函数的神经网络的混沌时间序列预测

权鹏宇1，车文刚2，周志元1，龙 婧1

(1. 昆明理工大学 信息工程与自动化学院，云南 昆明 650500；2. 昆明理工大学 云南省计算机技术应用重点实验室，云南 昆明 650500)

本文提出了以时间延迟坐标嵌入方法为基础的周期性波动预测模型。此模型使用一种叫作具有加权模糊隶属函数的神经网络的神经模糊网络（NEWFM）。在主要综合指标的预处理时间序列中使用了时间延迟坐标嵌入方法，并将此序列用作此神经模糊网络的输入数据来预测商业周期。以小波变换为基础使用其他方法进行了对比性研究，并对性能比较进行了主成分分析。使用线性回归分析来测试预测结果，以比较输入数据与目标类别，国内生产总值的近似值。另外两个模型忽略了基于混沌的模型捕捉非线性动态模型和系统中的相互作用。检验结果表明基于混沌的方法能够有效地增强预测能力，因此表明此方法比其他方法具有更优越的性能。

加权模糊隶属函数；时间坐标嵌入；混沌时间序列预测；模糊神经网络

0 引言

全球金融网络的复杂性和维度的不断增加导致金融市场的不确定性环境正在发生不同寻常的变化，因此很难使用传统经济模型来分析这种混沌的金融环境。除了一些新型经济模型使用了人工智能之外，最近已经开发了一些基于混沌的方法来处理变化的金融环境。

本研究主要关注基于混沌的方法，例如时间延迟坐标嵌入方法，这种方法使用了NEWFM来预测商业周期。早期对混沌时间序列研究的关注点主要是确定在这些系统中是否存在非线性动态行为。然而，最近的研究都在关注应用基于混沌的知识来提高预测的准确性。基于混沌的模型能够提高短期预测的准确性现在已经达到了广泛的认可[2]。

使用自互信息和Cao’s函数可以确定时间延迟和嵌入维度的参数，并用这些参数来重构相空间。在主要综合指标的预处理时间序列中使用了时间延迟坐标嵌入方法，并将此序列用作NEWFM的输入数据来预测商业周期[23]。使用线性回归分析对比了具有和不具有基于混沌预处理过程的预测结果，结果表明基于混沌的方法能够有效地增强预测能力，因此表明此方法比其他方法具有更优越的性能。

1 实验数据与方法

1.1 数据

经济指标是经济分析中的关键因素，能够表示出经济周期中的转折点和水平线[24]。特别地，主要综合指标（LCI）的组成要素是从整体经济成分中选择出来的非常敏感而且顺应周期变化的指标，并且通常在经济发生变化之前就会变化。因此，我们选择的样本阶段能够合理的评估经济周期分析的效果。

在本文中，使用了从1991年1月至2006年12月之间的192个LCI要素，包括就业职位求供比率、库存循环指标、消费期望和收到的机械订单。这些数据集都来自国家统计办公室。使用GDP平均增长率来作为类别0和类别1的目标临界值，GDP代表了国民经济的总体活动，并将月度GDP数据进行了分类（表1）。

1.2 特征选择

特征选择是神经网络中的非常重要的要素，能够通过降低维数来提高分类精确度并简化预测过程。我们使用NEWFM机器选择方法，也叫做NEWFM的非重叠分布方法（NADM）来降低选择重要输入时的维度，同时能够删除不重要的输入（图1）[25-28]。

NADM选择特征时使用的标准以非重叠区域为基础。图1给出了一种BSWFM（图5），这种BSWFM由使用LCI要素作为输入特征的三个加权模糊隶属函数得到。例如，将LCI的要素之一——收到的机械订单作为第i个输入特征时，蓝色区域（AiC）代表类别0中更大的模糊值，而红色区域（Aie）代表类别1中更大的模糊值。如果区域AiC+ Aie很大，并且每个区域都是平均分割的，那么这两个类别就更容易区分。区域越大，特征就越重要（图1（b））。第i个输入特征的非重叠区域分布启发函数可以通过以下式子计算得到：

表1 使用的经济指标Tab.1 Used economic indicators

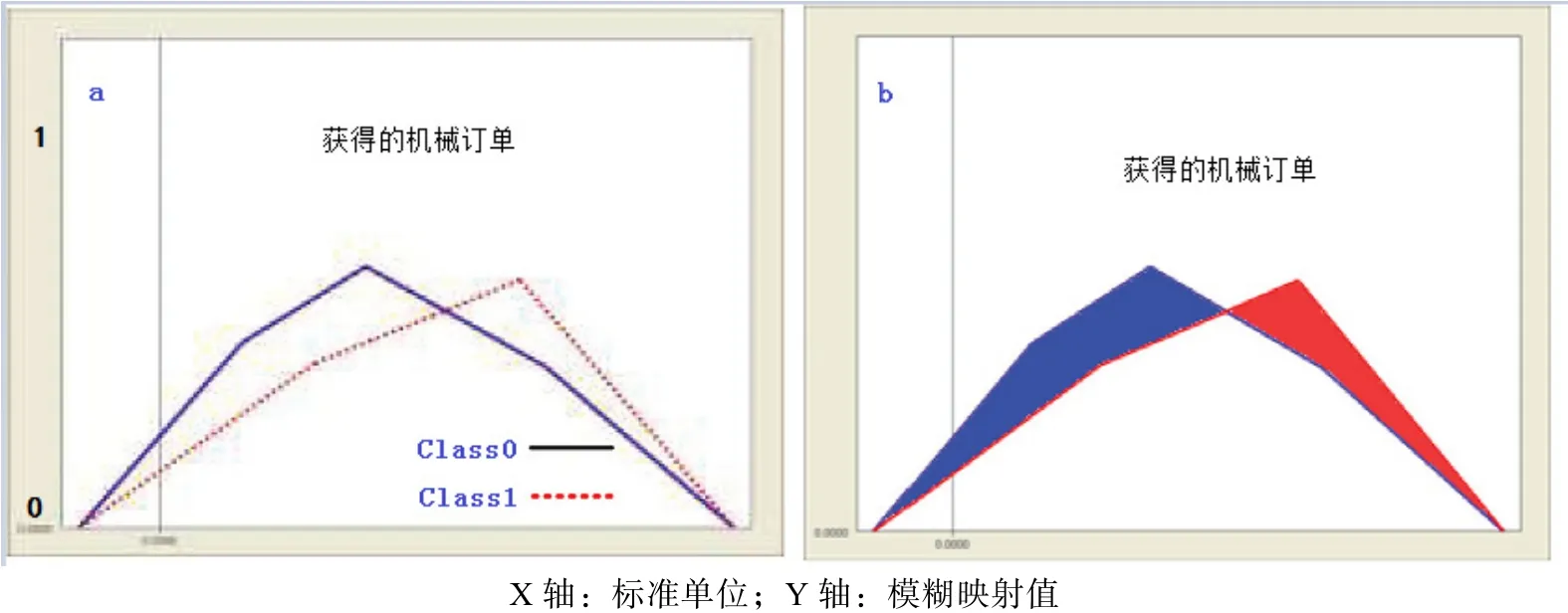
图1 NEWFM的非重叠区域分布示例Fig.1 Example of non-overlapping area distribution for NEWFM

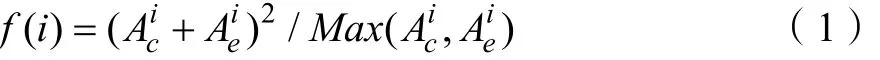
以特征的重要性为基础，在通过逐个减少输入特征进行数次分类实验之后，使用最佳子集的十个LCI要素结果中减少的七个特征来预测商业周期。

1.3 具有混沌时间序列的商业周期预测方法

我们对全球金融网络的复杂性和维度的不断增加导致金融市场的不确定性环境正在发生不同寻常的变化进行了检验。在这里，基于混沌的方法集主要关注外生因素本身，基于混沌的模型能够捕捉非线性动态行为和系统中的相互作用。这种基于混沌的预测方法为我们处理混沌的经济市场提供了一种新的方法[29]。

由于我们仅仅对标量（或者是单变量）数据集进行了检验，因此我们必须对轴线包含时间序列数据集的相空间进行重构，以确定初始动态系统。为了重构相空间，我们估算了嵌入维度和时间延迟的参数，并使用这些参数对相空间进行了重构[1-2]。

使用一些参数对LCI要素的时间序列进行预处理，然后使用这些时间序列作为NEWFM输入节点中的输入数据，如图4所示。

针对不同的经济环境这七个LCI要素中的每一个都代表不同的信息。进行重复实验之后，使用NEWFM将这些信息进行整合。图2给出了商业周期方法的示意图。

2 混沌时间序列分析和预测商业周期的结果

2.1 混沌时间序列分析与结果

2.1.1 相空间参数的选择

根据广泛使用的嵌入式Takens理论，嵌入维度m（m＞2d+1）适合于维度为d的动态系统相空间重构。然而，其他研究者认为嵌入维度m（m＞d）就足够了[2]。

在众多计算方法中，我们使用了Cao’s方法[4]，用这种方法能够有效清楚地区分确定性信号和随机信号，并通过较少的数据来确定时间序列需要的嵌入维度m。

对于时间延迟选择方法，我们使用的是互信息方法。通过计算连续点的依赖关系能够确定合适的延迟时间值。公式定义如下：

其中i是样本总数，P(Xi,xi+1)是测量值Xi和xi+1的联合概率密度，P(Xi)和P(xi+1)是Xi和xi+1的边际概率，最优延迟时间T对应最小的函数I(τ)。

2.1.2 混沌特征的识别

为了识别混沌特征，很多研究中都是用了关联维度和Lyapunov指数。使用关联方法能够估算时间序列的相关维度。如果系统是混沌的，那么相关维度应该是正数。相关子可以使用半径r和分数维形C(r) ∝ a * rDc来表示，其中a是常数，Dc为：

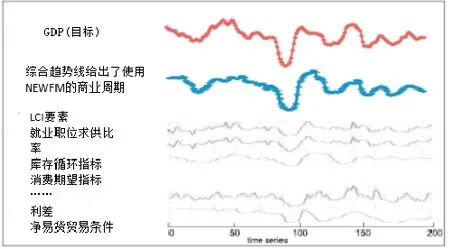
图2 商业周期预测方法示意图Fig.2 Business cycle prediction method diagram

可以使用Lyapunov指数来计算动态系统中相邻轨迹和混沌程度的指数发散度。其中每一个维度都存在一个指数，如果有一个或多个Lyapunov指数是正数，那么系统就是混沌的。因此，只需要计算最大的Lyapunov指数。第i个Lyapunov指数定义为：

2.1.3 相关参数和系数的计算

使用软件包TSTOOL可以找到相关参数，并确定时间序列的混沌特征。对于标量输入信号（图3（a）），我们尝试着包含更长的时间阶段，并追溯到1971年。将444个时间序列中较长的数据集用做输入矢量，其中包括样本阶段的192个时间序列，商业周期预测见表1。

第一，嵌入到TSTOOL中的自互信息函数（自互）能够帮助我们通过使用自互信息函数中的最小值为时间延迟τ找到合适的值。自互信息函数表明在相空间重构过程中x轴对应的延迟时间如图3（b）所示。

第二，Cao’s方法使用了一个改进的虚临位方法，并计算了时间序列的嵌入维度m。使用上述时间延迟参数作为输入数据，可以使用Cao’s方法在x轴上给出一个合适的最小嵌入维度（图3（c））。图4（d）给出了使用嵌入维度3和时间延迟1作为输入信号的时间序列的时间延迟重构。不幸的是，时间序列的长度不足以给出一个合适的吸引子几何图线。

第三，图3（e）给出了关联总和与半径的双对数坐标图的范围。输出，也就是斜率的值达到了2.3040，这是一个非整数分形维度，同时也证明了使用的数据集具有混沌特征。

最后，图3（f）给出了预测误差的范围。使用Lyapunov算法通过预测误差计算了相邻轨道距离的平均指数增加量。预测时间导致的预测误差的增大会产生一个最大的Lyapunov指数。检验结果（图3（f））表明最大的预测误差大约为+2.2，这个值表示使用的时间序列存在混沌特征。

图3 TSTOOL的应用结果Fig.3 Application results of TSTOOL

2.2 使用基于NEWFM的时间延迟坐标嵌入来

预测商业周期（混沌-NEWFM）

2.2.1 NEWFM的特征

为了预测未来的时间序列值，我们使用观测到的时间序列x1, x2, x3, ……, xn来预测混沌时间序列中的相空间[30]，使用当前的状态Xi可以通过下式来计算未来的状态Xi+T：

其中T为前置时间。将模糊神经网络，也就是NEWFM作为整个相空间的近似值。将嵌入相空间矢量Xi作为NEWFM的输入数据，并且可以表示为：

其中xi为时间ti时的观测数据，m为嵌入维度，τ为时间延迟。

NEWFM同时具有分类和特征选择的功能，因此也被称为NADM。NEWFM包含三个层次，分别为输入节点（xi）、超盒图节点（Bi）和分类节点（Ci）（图4）。可以对隶属函数的位置和权重进行适应性训练。经过反复训练之后，超盒图节点中的模糊设置会被整合到加权模糊隶属函数的界限总和中（BSWFM）（图5）[25]。这些BSWFM都是由三个加权模糊隶属函数产生的，并且包含类别0和类别1的规则（图1（a）），可以用作预测的模糊规则。另外，使用NADM可以调取最小的模糊规则，因此可以使用压缩模式进行最终的商业预测。

将第i个模糊中的BSWFM设定为Bim(x)，那么μib(x)定义为：

LCI要素的预处理时间序列见方程（5），将其用作NEWFM的输入数据可以预测商业周期。整体的机制，也就是所说的混沌NEWFM，如图4所示。

2.2.2 使用NEWFM进行分类

将1991年1月至2005年12月之间LCI要素的预处理月度数据作为训练数据和2006年1月至2006年12月之间的月度数据作为测试数据，具体见表1。使用最小的模糊规则进行预测，例如七个BSWFM中的每一个都包含类别0（谷底）和类别1（峰值）的规则，如图1（a）所示。

在学习过程中经过3000次重复之后，训练数据对应的分类率为93.19%，非训练数据对应的分类率为91.66%。表2给出了最终的分类性能。

3.2.3 去模糊化和商业周期趋势线

使用BSWFM的预测结果能够得到商业周期趋势线，然后使用Sugeno模糊模型对其去模型化[21]。在这里，可以在不消耗时间和进行数学去模糊化操作的条件下对模糊神经网络的输出数据进行处理。

图4 使用时间延迟坐标嵌入的混沌NEWFM结构Fig.4 The use of time delay coordinates embedded in the chaotic NEWFM structure

图5 3个加权模糊隶属函数的界限总和（BSWFM，粗线）Fig.5 Boundary Sum of 3 Weighted Fuzzy Membership Functions(BSWFM, Thick line)

表2 NEWFM的分类性能Tab.2 NEWFM classification performance

在IF-THEN规则的模糊推理系统中，Sugeno模糊模型的主要差别就是输出数据为加权平均值[29]，最终输出数据z是所有规则输出数据的加权平均值，可以使用下式计算：

其中，wi为第i个输出数据的加权平均值，而zi是结果部分中IF-THEN规则的第i个输出数据。

整合预测结果给出了具有目标分类的相同波动，即GDP。GDP和混沌NEWFM的对比曲线如图6所示。混沌NEWFM线是根据1991年1月至2005年12月之间的3000次重复所产生的混沌NEWFM模糊规则预测得到的结果。

3 对比研究与结果

对于使用和不使用混沌模型的预测能力对比，我们以小波转换和主要要素分析为基础添加了使用相同数据集的其他预测模型。

3.1 使用基于NEWFM的小波转换方法（小波NEWFM）对商业周期进行预测

小波是指有限时间内的波形，可以通过转换（时间变换）和缩放来表示信号过程，因此能够产生小波系数。小波能够保证信号的低频要素，也就是近似值，并且能够检验高频要素，详细值[33]。因此，我们在分析时间序列时能够得到短时间内的光滑运动图线和阶段性运动。

可以使用小波函数Ψ（.）对信号的小波转换，也就是时间序列x（t）进行分析，Ψ（.）定义如下：

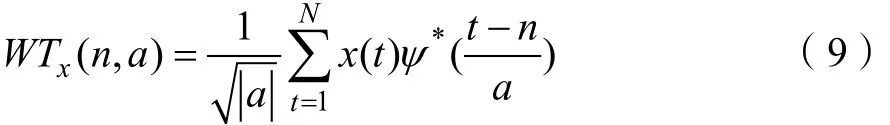
其中，Ψ*（.）为基本小波函数，a是缩放参数，n是转换参数。

图6 混沌NEWFM的预测结果Fig.6 prediction results of chaos NEWFM

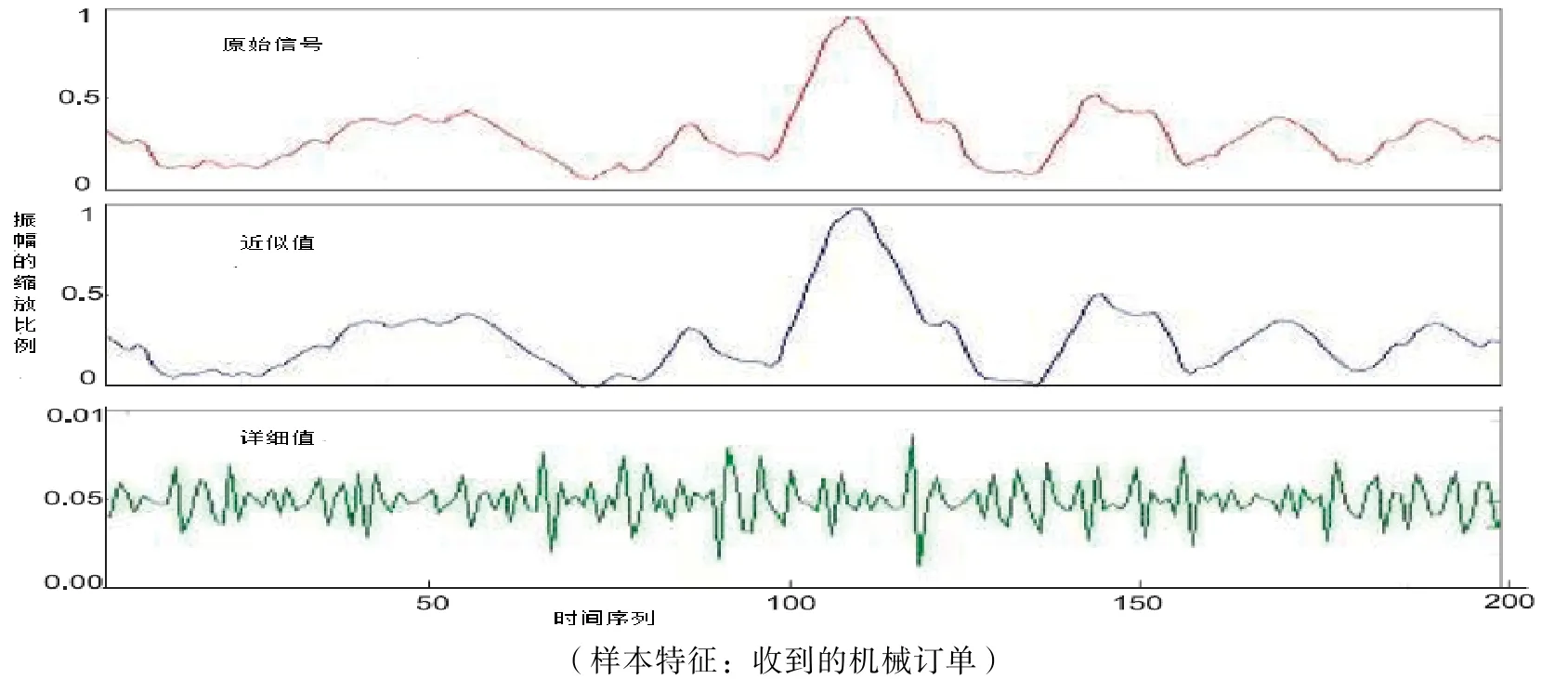
图7 在水平1上使用Daubechies 4的分解样本Fig.7 Sample decomposition on level 1 with Daubechies 4

在此，我们使用Daubechies 4，一种广泛用于不稳定数据集的小波[31-33]。使用MATLAB计算得到的时间序列的分解样本如图7所示。

NEWFM的输入部分是在水平1上使用Daubechies 4分解得到的时间序列的7个合成近似值。不幸的是，使用更加平滑的数据进行的实验无法实施，因为样本时间序列的长度不足以进行进一步的分解。使用这些输入数据对神经网络进行超过3000次重复训练，图9（b）给出了以小波转换为基础的商业周期的预测结果。

3.2 基于NEWFM使用主要要素分析（PCANEWFM）预测商业周期

主要要素分析（PCA）能够将时间序列转化成新的非相关变量，也叫做使用协方差矩阵的主要要素。PCA结果表明输出数据由特征值（例如主要元素的变量）、所占比例和总体变量的累积比例，以及每个主要要素的系数组成（表3）。

我们选择了相同数量的累积特征值为95.4%的 7个要素，这些要素能够解释表3和图8中所有的模型变量。经过3000次重复学习后，将7个要素作为NEWFM输入数据的预测结果见图9（c）。

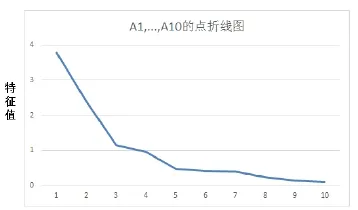
图8 使用MINITAB计算得到的PCA点连线图Fig.8 PCA point connection diagram Calculated by MINITAB

表3 使用MINITAB进行的主要要素分析Tab.3 Main factor analysis using MINITAB

表4 分类性能对比Tab.4 Classification performance comparison

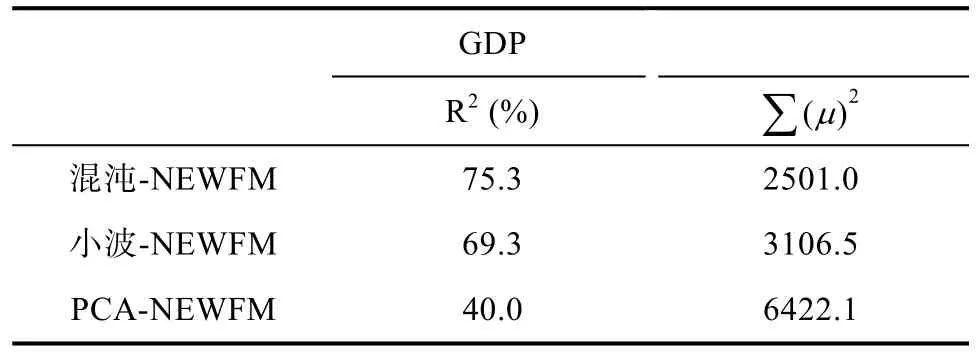
表5 线性回归分析的总结Tab.5 Summary of Linear Regression Analysis

4 预测能力对比和讨论

4.1 预测能力对比

表4给出了使用三个输入部分时通过三种方法得到的NEWFM结果的分类对比。每一个NEWFM都使用1991年1月至2005年12月之间的三个输入部分进行了3000次重复训练。分别使用训练数据（1991年1月至2005年12月）和非训练数据（2006年1月至2006年12月）进行分类。最终分类结果表明混沌NEWFM的分类率优于其他方法。因此，混沌NEWFM显示在图9中的预测趋势线和GDP之间存在更好的近似值。

为了对比输入数据作为目标类别预测指标的近似性，我们使用线性回归分析对每一种方法对应的两条趋势线之间的相似性进行了检验[17]。表5和表6给出了使用MATLAB进行的线性回归分析结果。将来自NEWFM、小波和PCA的时间序列处理作为解释变量，而GDP作为目标变量。使用确定系数R2的混沌NEWFM类似性的程度优于小波NEWFM和PCA-NEWFM（表5）。

确定系数R2代表模型的解释能力，定义为：

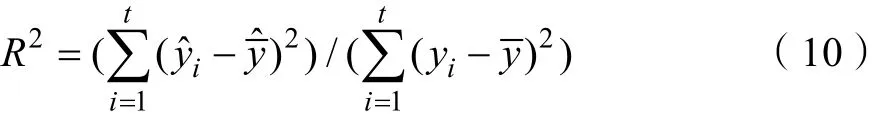
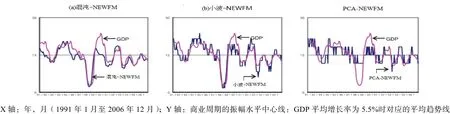
图9 不同方法预测的时间序列Fig.9 time series predicting in different methods

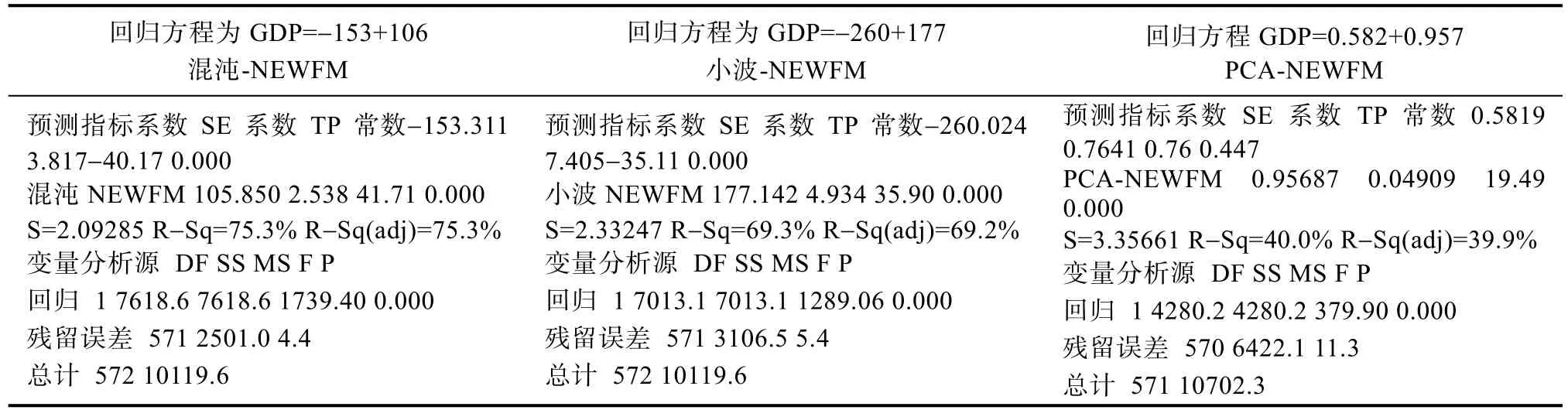
表6 使用MINITAB进行线性回归分析的结果Tab.6 The results of linear regression analysis using MINITAB

4.2 预测质量讨论

图9（a）中基于混沌的模型使用时间延迟嵌入方法来捕捉非线性动态模型与相互作用，而忽视了另外两个模型，尽管模型构建是一个非常复杂的任务。因此，我们能够确定基于混沌的模型使用的适应性数据适合于系统，在时间序列分析中有很大的优越性。

图9（b）中小波NEWFM模型使用了Daubechies 4在水平1上分解的预处理数据，表明其性能低于混沌NEWFM。不幸的是，使用更加平滑的数据在超过水平1上进行的进一步实验无法实施，因为样本时间序列的长度无法进行进一步的分解。

图9（c）中PCA-NEWFM使用最新的转换数据集作为NEWFM的输入数据，证明了这种方法最不具有优越性。最大变量上噪音的减少是PCA的主要优势，这可以降低预测质量和存储的计算需求。然而，这种优势似乎会对需要敏感性的模式识别能力产生不良影响。

5 结论

本研究探究了使用具有NEWFM的基于混沌的模型，例如时间延迟坐标嵌入模型来预测商业周期。对带有或不带有混沌模型的性能进行分析表明混沌NEWFM能够捕捉非线性动态模型和相互作用，这表明其具有更高的分类精确度。因此可以在预测趋势线和目标分类GDP之间得到一个更好的近似值，从而确定这种模型是整体经济情况中较好的预测指标。在混沌经济的情况下，基于混沌的模型在预测商业周期时能够提供一个新的角度，从而对维度和复杂度不断增加的金融市场的混沌特征有一个新的认识，因此可以处理全球经济面临的问题。

另外，需要使用足够长的时间序列来进行进一步的研究，从而提出吸引子的形状，并对两种预测模型进行更好的对比。

[1] Zang Jun, Chung HenryS, Lo Wai-Lun. Chaotic time seriesprediction using a neuro-fuzzy system with time-delay coordinates. IEEE Trans Knowl Data Eng 2008, 20(7): 956-64.

[2] Karunasinghe DulakshiSK, Lion Shie-yYui. Chaotic time series prediction with a global model: artificial neural network. J Hydrol 2006; 323: 92-105 .

[3] Jianuo Zhou, Tao Bai, Aiguang Zhang, Jiming Tian, “Forecasting share price us- ing wavelet transform and LS_SVM based on Chaos theory,” School of Business Administration, North China Electric Power University, Baoding, China.

[4] 张吉礼. 模糊神经网络控制原理与工程应用[M]. 哈尔滨:哈尔滨工业大学出版社, 2004. ZHANG J L. Fuzzy Neural Network Control Principle and Engineering Application[M]. Harbin: Harbin Institute of Technology Press, 2001.

[5] 许传华, 任青文, 房定旺. 基于神经网络的混沌时间序列预测[J]. 水文地质工程地质, 2003(1): 30-32. XU C H, REN Q W, FANG D W. Chaotic Time Series Prediction Based on Neural Network[J]. Hydrogeology and Engineering Geology, 2003(1): 30-32.

[6] 向小东. 基于混沌理论与径向基函数神经网络的混沌时间序列预测[J]. 福州大学学报, 2003(8): 401-403. XIANG X D. Prediction of chaotic time series based on chaotic theory and radial basis function neural networks[J]. Journal of Fuzhou University, 2003(8): 401-403.

[7] Bashirov A E, Belaghi M J S. On application of euler’s differential method to a continued fraction depending on parameter[J]. Indian J of Pure and Applied Mathematics, 2014, 45(3): 285-295.

[8] Tian N, Lai C H. Parallel quantum-behaved particle swarm optimization[J]. Int J of Machine Learning and Cybernetics, 2014, 5(2): 309-318.

[9] Manickavelu D, Vaidyanathan R U. Particle swarm optimization(PSO)-based node and link lifetime prediction algorithm for route recovery in MANET[J]. EURASIP J on Wireless Communications and Networking, 2014, 2014(107): 1-10.

[10] 韩敏, 王迎新. 多元混沌时间序列的加权极端学习机预测[J]. 控制理论与应用, 2013, 30(11): 1467-1472. HAN M, WANG YX. Multivariate chaotic time series prediction based on weighted extreme learning machine[J]. Control Theory and Application, 2013, 30(11): 1467-1472.

[11] Sharif Md. Raihan, Yi Wen Bing Zeng, “Wavelet: a new tool for business cycle analysis, ”FRB of St. Louis Working Paper 2005-050A, 2005.

[12] Minitab Inc., “Minitab Release 14,” published 2005.

[13] Takens F. Detecting strange attractors in turbulence. Dynamical systems and Turbulence, 898. Springer Berlin Heidelberg; 2006. p. 366-81.

[14] 邵小强, 马宪民. 混沌时间序列预测的建模与仿真研究[J].计算机仿真, 2011, 28(4): 100-102. SHAO X Q, MA X M. Modeling and Simulation of Chaotic Time Series Prediction[J]. Computer Simulation, 2011, 28(4): 100-102.

[15] 张淑清, 贾健, 高敏, 韩叙. 混沌时间序列重构相空间参数选取研究[J]. 物理学报, 2012, 59(3): 1576-1582. ZHANG S Q, JIA J, GAO M, HAN X. Study on the parameters determination for reconstructing phase-space in chaos time series[J]. Journal of Physics, 2012, 59(3): 1576-1582.

[16] Tagaki T, Sugeno M. Fuzzy identification of systems and its application to mod- eling and control. IEEE Trans SMC 1985; 15: 116-32 .

[17] Sasan Karamizadeh Shahidan. An overview of principal component analysis. J Signal Inf Process 2013; 4: 173-5 .

[18] Cao Liangue. Practical method for determining the minimum embedding di- mension of a scalar time series. Physical D. 1997; 110: 43-50 .

[19] The Bank of Korea The Korean business cycle. Mon Bull 2004: 31-53 .

[20] Lim JS. Finding features for real-time premature ventricular contraction de- tection using a fuzzy neural network system. IEEE Trans Neural Networks 2009; 20: 522-7.

[21] Lim JS. Finding fuzzy rules for iris by neural network with weighted member- ship functions. Int J Fuzzy Logic Intell Syst 2004; 4(2): 211-16.

[22] Lim JS. Feature selection using weighted neuro-fuzzy membership functions. In: The 2004 international conference on artificial intelligence(IC-AI’04), 1; 2004. p. 261-6 .

[23] Lim JS. Feature selection by fuzzy neural networks and the non-overlap area distribution measurement method. Korea Fuzzy Logic Intell Syst Soc 2005; 15(5): 599-604.

[24] 修妍. 基于改进相空间加权局域法的混沌时序预测[J]. 软件, 2013, 34(4): 34-37.

[25] 张伟杰. 基于模糊多智能体的决策算法设计[J]. 软件, 2014, 35(1): 39-42.

[26] 高家明, 薛京生, 肖涛. 基于支撑向量机回归的接警量预测与比较[J]. 软件. 2013. 34(7): 77-80.

[27] 来金钢, 周洪, 胡文山. 微电网环境下光伏发电短期输出功率预测研究[J]. 新型工业化, 2014, 4(12): 5-11.

[28] 张晔, 魏然, 谷延锋, 等. 基于小波变换的光谱异常特征分析及提取技术研究[J]. 新型工业化, 2013, 3(1): 38-45.

Prediction of Chaotic Time Series Based on Neural Networks with Weighted Fuzzy Membership Functions

QUAN Peng-yu1, CHE Wen-gang2, ZHOU Zhi-yuan1, LONG Jing1
(1. School of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500, P. R. China; 2. Yunnan Provincial Key Laboratory of Computer Technology Application, Kunming University of Science and Technology, Kunming 650500, P. R. China)

This study presents a forecasting model of cyclical fluctuations of the economy based on the time delay coordinate embedding method. The model uses a neuro-fuzzy network called neural network with weighted fuzzy membership functions (NEWFM). The preprocessed time series of the leading compos- ite index using the time delay coordinate embedding method are used as input data to the NEWFM to forecast the business cycle. A comparative study is conducted using other methods based on wavelet transform and Principal Component Analysis for the performance comparison. The forecasting results are tested using a linear regression analysis to compare the approximation of the input data against the tar- get class, gross domestic product (GDP). The chaos based model captures nonlinear dynamics and interac- tions within the system, which other two models ignore. The test results demonstrated that chaos based method significantly improved the prediction capability, thereby demonstrating superior performance to the other methods.

Weighted fuzzy membership functions; Time delay coordinate embedding; Chaotic time series prediction; Neuro-fuzzy network

TP391.9

A

10.3969/j.issn.1003-6970.2017.05.006

权鹏宇(1993-)，男，硕士研究生，主要研究方向：云计算、时间序列分析、模式识别；车文刚(1963-)，男，教授，博士后，主要研究方向：人工智能、模式识别、时间序列分析、计算机应用；龙婧(1991-)，女，硕士研究生，主要研究方向：时间序列分析、模式识别；周志元(1992-)，男，硕士研究生，主要研究方向：时间序列分析、模式识别。

本文著录格式：权鹏宇，车文刚，周志元，等. 基于具有加权模糊隶属函数的神经网络的混沌时间序列预测[J].软件，2017，38（5）：98-106