基于复杂网络的我国信贷风险问题研究
张昴 聂广礼
摘要:近年来,我国商业银行不良贷款率升高,信贷投放面临着行业和客户的选择困难。但是,现阶段我国仍缺乏关于行业资金投放的理论和方法。本文利用复杂网络的方法研究经济系统中行业的信贷风险,提出地位系数这一指标来衡量局部行业间投入产出网络的对称性。然后,考察地位系数与KMV模型中行业违约距离之间的负相关性,并根据宏观经济以及国家政策对低风险和高風险行业的地位系数进行对比说明。最终,提出了切实可行的政策建议。
关键词:信贷风险;投入产出网络;行业地位系数;KMV模型
文献标识码:A 文章编号:1002-2848-2017103)-0032-08
一、引言及文献综述
银行信贷是推动地区繁荣和发展的主要力量,银行不合理的信贷配置状况会增加信用风险。近年来我国商业银行不良贷款率上升,商业银行的信贷风险控制问题亟需解决。
李克强总理在2016年人大四次会议中外记者会上表示,通过市场化债转股的方式来逐步降低企业的杠杆率。债转股是消化商业银行不良贷款的一种后发方式,但是要从根本上降低商业银行不良贷款,就应该从贷款投放上人手。在信贷结构调整中,行业是改善商业银行信用风险的一个重要维度。但是,从理论上来看,我国尚未建立有效的信贷风险的计量模型,更缺乏行业层次上的指导性措施;从实践上来看,银行信贷投放的行业是高度相似的。
目前,理论界对商业银行信贷投放是集中还是分散这一问题已经有了比较丰富的研究成果。如现代资产投资组合理论指出“不要把鸡蛋放在一个篮子里”,适度的投资分散化可以有效地降低系统性风险。Douglas w.Diamond指出,贷款分散可以减少银行陷入财务困境的概率。在行业层次上,《巴塞尔协议Ⅲ》指出,由单一风险因子敞口过大而造成的行业集中度风险是造成银行信贷问题的重要原因。国内学者巴曙松等也指出,贷款集中度风险是导致银行发生危机的主要原因之一。
长期以来,国内外的研究成果显示,无论是监管当局还是银行自身的风险管理,都将信贷投放分散化作为完善商业银行信贷结构的重要措施。但是,这一看似完美的逻辑在银行信贷领域却未必是正确的。信贷集中在很大程度上会造成银行的风险聚集,但是信贷分散却并不必然导致银行的风险分散。那商业银行如何选择信贷投放的行业,来达到分散自身风险的目的就成为一个十分有意义的议题。
对于这一问题的研究,李卫东等将价值投资理论引入了商业银行的信贷决策研究中,他使用了“压力测试”的技术分析某行业的信贷投资风险,并结合产业结构的调整政策,结果发现对于某股份制商业银行而言,建筑业和批发零售业是理想的信贷投向目标。聂广礼也提到,我国信贷投向呈现出所属行业高度相似的特点。其中,制造业和交通运输业是最集中的信贷投放行业。
但是,鉴于我国关于行业的某些重要数据的不可得性,以及单一的研究视角,目前众多文献的说法都没有一定的系统性。Daron Acemoglu提出了经济系统波动的网络起源这一说法,即由于金融市场的复杂性,单一机构的金融风险最终可能演变为整个金融市场的系统性风险。简而言之,就是网络的不对称程度越高,这个经济体网络的风险就越大。因此,复杂网络可以作为一个切入点来分析行业在整个经济体中的风险程度。
就经济领域而言,近年来复杂网络理论已经得到了广泛的应用。目前国内外对于复杂网络在信贷方面应用的研究主要在两方面。一方面是采用复杂网络技术或者统计学理论进行推导,探讨信贷风险的传播路径。比如在个体微观层次上,Battiston等构建了“企业——金融机构”的二分网络模型,研究银行合作网络和企业信贷关系网络的各自特征。Augusto Hasman首次利用IMF提出的信用额度方法,通过研究银行间危机的传播路径,提出了预防危机传播的机制。另一方面,应用复杂网络技术着重分析信贷网络的拓扑特征。鉴于数据的可获得性,该领域的研究大多是对银行间市场风险暴露数据的建模分析,并证明金融网络具有典型的复杂网络特征。例如,Giulia Iori等通过研究不同规模银行之间的行为差异,以及它们的结构演变,进而帮助监管机构评估银行市场的效率。然而,这类研究还停留在统计特征的描述阶段,很少关注网络拓扑特征间的关联与拓扑特征对网络功能的影响,没有阐述信贷不合理现状的网络机理,因此未能提出提高信贷系统稳健性的理论措施。
本文致力于解决银行信贷的行业投向问题,从行业波动的网络起源这一角度出发,试图用行业系数来衡量某个行业在整个经济体网络中所处的地位,以便为商业银行的信贷投放及风险规避提供理论依据。
本文的主要贡献体现在:第一,创新性地提出了地位系数这一概念,用以衡量某个行业在整体行业网络中所处的地位,进而判断该行业的风险,并在行业层次上为银行规避信贷风险提供理论指导。第二,从衡量整体网络的对称性过渡到衡量局部网络的对称性,合理推测出局部网络对称性与波动性的关系。第三,利用多阶互联代替一阶互联,更加完善地衡量了投入产出网络中行业之间的级联效应。
本文安排如下:第二部分是行业地位系数的理论概述及数据的选取;第三部分是对地位系数的实证检验以及实际应用;第四部分是本文的结论及政策建议。
二、研究思路与数据
(一)研究的理论基础
1.网络不对称性和总波动的关系
根据Acemoglu的论证,在一个投入产出网络中,网络的波动性可以用如下式子衡量:
公式(1)表明整个网络的不对称性与网络总波动存在着正向关系。同时考虑不同部门之间的一阶、二阶互联关系,不仅表明了一些行业是大的供应商的事实,也蕴含着更加微妙的理念,即存在着一个行业的显著聚集区,这是由它们有共同供应商的事实造成的。
2.聚集系数
这是表示一个网络中节点的聚集程度。假设节点i的度为ki,即它有ki个邻节点(直接有边相连)。如果节点i的ki个邻节点之间也两两相连,那么在这些邻节点中就存在ki(ki-1)/2条边,这是边数最大的情况。在实际情况中,ki个邻节点未必两两相连。于是,我们将网络中的度为ki的节点的聚集系数定义为:endprint
(4)
一个网络的聚集系数C定义为网络中所有n个节点的聚集系数的平均值,即:
(5)
显然有0≤C≤1,当C=0时,网络中所有节点的聚集系数都为0;当C=1时,网络中所有节点的聚集系数都为1,此时网络中任意两个节点都有连线,成为全局耦合网络。
3.网络中的不对称性
对称性的概念来源于自同构,节点集的自同构可以看作节点的一种重新排列,在重新排列的同时保留原来的邻接节点。如果潜在的网络图形仅包括一种排列变换,那么网络是不对称的,反之则是对称的。
普遍意义下的图形对称有连续对称、不连续对称、随机对称等。在很多文献中,对称性被定义为在改变给定的一组顶点集合的条件下,相邻顶点之间关系的不变性。相似的连接模式意味着有相同属性的节点趋于拥有相似的连接目标。以朋友之间的网络为例,有相似属性(教育背景、兴趣、年龄)的人,可能有相同的朋友。但是也有很多文献不拘泥于不对称的原始定义,而是根据需要采用新的方式重新衡量不对称性程度。Acemoglu则将部门间的不对称程度用网络中度序列的变异系数和二阶互联系数来衡量。Ben D.MacArthur认为,网络自同构在变换节点的同时并没有改变邻接节点,所以对称性网络有一定程度的结构冗余度。我们可以用自同构组结构来精确衡量这种冗余度,利用对称性将网络分解成不可约的因素的乘积,然后将其分别对应于对称的子网络进而研究普遍意义下网络的对称性。
(二)对网络节点局部对称度的定义
现有文献大部分都是从整体结构出发,找出某个指标衡量整个网络的对称性。由于本文旨在寻求网络中某个节点在整个网络中的对称性地位,因此本文另辟蹊径,从聚集系数出发,定义节点i的地位系数这一概念。
考虑一个经济体{εn}kn∈R,包含n个行业,行业间投入产出网络(局部图)如图1所示。不同的节点代表不同的行业,行业间的有向线段表示某行业对另一行业的投入,其中双向有向线段表示两者互相投入。
各个行业之间的投入產出关系可以表示为一个n×n的矩阵,矩阵中的单位(i,j)代表第i个行业对第j个行业的投入。为了方便计算,我们用矩阵表示网络中节点和边两个要素。如下所示:
其中,aij为矩阵中的元素,当从节点i到节点j有连线(单向连线)时,aij=1;否则aij=0。
定义:若一个有向网络中的节点i有m个节点与之相邻,则将节点i在此包含m+1个节点的局部网络中的地位系数Si定义为网络中实际与i相连的边数(i的主子式)与全连接情况下边数的比值。记为:
(三)地位系数合理性的理论证明
下面分两步证明地位系数在刻画节点在网络中地位的合理性。
当节点i的相邻节点不变(此时m固定),增加此子网络的边数,则地位系数Si的分母不变,分子变大。显然此时节点i在子网络中的地位增强,子网络更加对称。
当节点i有(M-m)个新的孤立的相邻节点(即这些新的节点只与节点i相连)时,则此时子网络中的边和节点均会增加,地位系数Si的分子分母都变大。即有:
(8)
易证.Si
(四)数据选取
我们需要使用我国投入产出表来计算行业地位系数。投入产出表分为投入产出流量表、投入产出直接消耗系数表,以及投入产出完全消耗系数表。完全消耗系数是生产单位最终产品对某种总产品或中间产品的直接消耗与间接消耗之和,可以由直接消耗系数得到。
由于投入产出网络中存在级联效应,也就是说一个上游行业不仅仅会影响它的下游行业,还有可能通过下游行业影响其它的行业。用另一种说法表述,度较高的部门之间可能有相同的供应商。于是我们认为行业间的高阶互联关系就对应于完全消耗系数表,投入产出完全消耗矩阵计算方法如下所示:
(9)
其中,Bn表示完全消耗系数矩阵,An表示直接消耗系数矩阵。等式右边的第一项代表j部门对i部门的直接消耗量,第二项代表j部门对i部门的第一轮间接消耗量,以此类推,第n+1项代表j部门对i部门的第n轮间接消耗量。
由公式(1)、(2)、(3)可以看到Aeemoglu的相关文章仅仅考虑了一阶互联和二阶互联的情形。其中,式(2)、(3)和投入产出系数表的An,A2n在衡量级联效应的作用上是一致的。而代数形式上的三阶互联是很难给出表达式的,不过我们从投入产出完全消耗系数表的矩阵表达上给出了对应三阶以上的级联表达,即Ain,从而完美衡量了从一阶互联到n阶互联的情形。因此本文采用完全消耗系数表来进行下一步计算。
标准的投入产出表每5年编制一次,我们选取最近的2012年表(2015年下半年公布)。我们选取的是139×139行业的完全消耗系数表,而不去选42×42,是因为42×42划分不够细致,几乎所有的节点都有连线,这样网络呈现高度对称性,遮掩了行业间不对称的特性。
三、实证检验及应用
(一)地位系数与行业信贷风险的相关性分析
1.行业信贷风险的考量
在《巴塞尔资本协议Ⅲ》中,巴塞尔银行监管委员会推荐使用KMV模型进行内部评级。KMV模型是一种利用现代期权定价理论对风险债券和贷款进行估价,从而构建的违约预测模型。它能够充分利用市场信用和历史账面资料在现代公司理财和期权定价理论的基础上进行“移植处理”。并且,我国很多学者的研究表明,KMV模型在衡量我国上市公司的信用风险方面具有较强的适用性。
为进一步论证第一部分提出的地位系数的合理性,我们将利用KMV模型计算网络中每个行业节点中所有企业的违约距离,并通过违约距离与地位系数之间的相关系数分析证明我们提出的行业地位系数——在一定程度上等价于行业因子,可以很好地衡量各个行业在整体网络中所发挥的作用。
关于数据的选取。由于我们选取的是2012年的投入产出数据,考虑到投入产出表每五年编制一次,为了对应每年的数据,我们选取相邻的5年数据。从一定程度上来看,2010、2011年的投资等投入会对2012年有重要影响,而2012年的产出有一部分又会作为对2013、2014年的投入。因此我们选取2010、201l、2012、2013、2014年各个行业所有上市企业作为样本,考察其违约距离。
本文选取Wind数据库中证监会有关分类办法下71个行业中的所有上市企业,并利用Wind数据库沪深证券交易所2010-2014年年报中所提供的总市值、长期负债和短期负债等财务数据,以及通过向前复权处理的2010-2014年股票的日成交收盘价数据进行分析。
由于我国国债市场尚不发达,不存在完全意义上的无风险利率(利率的确定并没有完全的市场化),本文在借鉴前人研究成果的基础上,选取中国人民银行2010-2014年公布的一年期定期整存整取存款利率作为KMV模型中的无风险利率,由于央行经常对利率进行调整,所以设定无風险利率为按全年天数加权平均后的利率。通过计算可得2010-2014年的一年期定期整存整取的无风险利率,见表1。
由表1可知,2010-2014年年的加权利率为分别为2.3%,3.28%,3.24%,3%,2.97%。
关于KMV违约距离的计算。KMV模型的最终输出结果是预期违约概率EDF,但是我国并没有完整的上市公司数据库。另一方面,在本文的分析中,只需证明地位系数的合理性,所以我们只需要计算出违约距离DD即可。
首先,根据股票价值及其波动性与资产价值及其波动性的函数关系,通过股票的收益率数据计算出股票价值和股票价值波动性,进而反向迭代估计出公司的资产价值和资产价值波动性,具体过程如下所示:
根据Black-Scholes-Merton期权定价模型,构建出股权价值与市场价值之间的函数关系:
(10)
然后,根据伊藤引理:
最后,根据公司负债计算出违约点DPT:
DPT=短期负债+50%长期负债 (13)
用第一步算出的资产价值乘以预期资产价值增长率预测出资产的未来预期价值,从而测算出违约距离DD,如下式:
(14)
其中,DD表示违约距离,E(VA)代表公司未来资产的期望值,DPT代表违约点,σA代表公司资产价值的波动率。本文利用Matlab 2014进行KMV违约距离的计算。
2.秩相关系数分析
我们在证监会行业分类和投入产出表行业分类一致的行业中,剔除上述KMV计算中指标缺失以及仅有少数企业的行业(不具有代表性),经过数据剔除后剩余38家有效行业,如表2所示:
计算每个行业所有企业的违约距离,然后做行业地位系数与违约距离的散点图,如图2所示。从图2可以看出全样本企业违约距离与所属行业地位系数呈现负相关关系。
由于地位系数是属于行业维度的,又考虑到各行业众多企业参差不齐,我们去掉其中违约距离最大和最小的个别企业,计算每个行业中企业违约距离的期望以代表该行业的违约距离。行业违约距离与行业地位系数分布如图3所示。
求得行业地位系数序列和行业违约距离序列的简单线性相关系数为-0.535。考虑到经济体的非线性,又考虑到等级相关系数可以较好地衡量非线性相关性,我们对两序列进行排序,计算Spearman相关系数,如表3所示。其中违约距离越大,代表该行业风险越高;地位系数越大,代表该行业风险越低。两者在理论上为负相关关系。
由表3可知,两序列的Spearman相关系数约为-0.659。违约距离序列和地位系数序列互不相关的检验值为0.000,否定原假设,认为违约距离序列和地位系数序列是显著相关的,两种方法对行业稳定性的排序存在一致性。
(二)地位系数的实际应用
1.高风险和低风险行业的地位系数
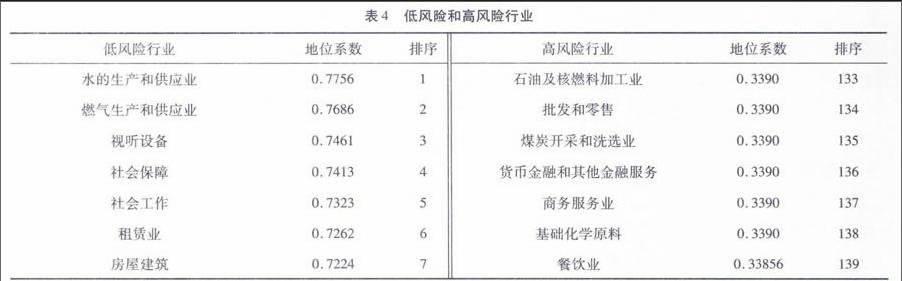
基于本文研究发现的行业地位系数和行业中企业平均违约距离的负相关关系,我们提出将国民经济的139个行业划分为低风险、中度风险、高度风险三个等级。其中,低风险和高风险行业占比各为5%。在此,仅列出2012年前后低风险和高风险的行业名称及其排序,如表4所示:
在表4中,排序越靠前,代表地位系数越高,说明这些行业所处的子网络更加趋近完全对称网络,其稳定性越高,风险越低。其中,低风险的7个行业分别为水的生产和供应业、燃气生产和供应业、视听设备、社会保障、社会工作、租赁业和房屋建筑;高风险的7个行业分别为石油及核燃料加工业、批发和零售、煤炭开采和洗选业、货币金融和其他金融服务、商务服务业、基础化学原料和餐饮业。
2.国家政策层面的原因解读
由表4我们可以看出,低风险行业大都是一些社会福利行业和基础服务行业,由于这些行业和其他行业关联紧密,且国家对其中某几个行业重点扶持,因此这些行业的投入产出较为稳定,波动较小,代表企业的违约风险就小。例如,对于水的生产和供应业,发改委等有关部门在2011年调整和修订的《产业结构调整指导目录(2011年本)》突出了水利设施在农业产业结构中的重要作用,将水的生产和供应业划入了国家鼓励类的行业条目。
而高风险的行业则主要属于金融、煤炭以及石油化工等领域,这些行业多属于国家高度集中管控的行业,投入产出效率低下,受国家政策调节的幅度较大,故而产出波动较大,风险较大,代表性企业的违约风险就较大。例如,《产业结构调整指导目录(2011年本)》大大减少了对有色金属、钢铁、化工等重工业的鼓励类条目。2012年起,由于我国的经济结构转型,导致市场需求不足,而煤炭供应却继续保持增长,开始形成了产能严重过剩的局面。endprint
四、结论与政策建议
利用投入产出网络,本文提出地位系数这一概念用来衡量某行业所处局部网络的对称性,并对其进行理论推导,证明其合理性。然后,选取与KNV模型可比较的38个行业,分别求出这38个行业的地位系数序列和违约距离序列,并且求其秩相关系数。发现秩相关系数高达-0.659并且显著。由此从实证角度说明本文提出的地位系数具有一定的实际意义。为了全面分析投入产出网络中各个行业地位系数与实际情况的差别,本文选取高风险和低风险(各占5%)的行业,并通过国家具体政策、宏观环境等因素分析论证其风险高或低的原因。最后,分别从银行信贷政策、行业自身发展以及投入产出表的角度提出如下具有针对性的政策建议:
第一,银行应将信贷投向行业地位系数较高的行业。本文的主要贡献就是在行业维度为银行的信贷投放提供一定的参考。基于行业不对称性和行业信贷风险的正向对应关系,本文建议商业银行在对不同企业投放信贷时,应该对企业所属的行业进行比较,参考行业地位系数,尽可能多的将信贷资金投向地位系数较高的行业,即低风险行业。同时,合理控制对具有较低地位系数的行业的信贷投放量。
第二,应尽量拓展行业间的业务联系。从行业自身的角度看,鼓励在科学研究的前提下做出一定的创新,探索不同部门间潜在的关系,分散化某行业的供应商以及下游行业,尽可能增加与其他行业的联系。如此,当一个行业受到某种冲击时,其传统的上下游行业因为有了与其他行业的联系,不至于损失过为惨重以至于引发金融危机。以“互联网+”为例,随着时代的进步,互联网与其他诸多行业交叉产生了很多新兴产业。互联网+餐饮产生了外卖,互联网+金融产生了支付宝、微信支付等等。它们结合在一起,把传统的生产消费升级,带给大众更好的體验,也为我国增加了大量的就业机会。同样,2015年“旅游+”战略的提出也将是产业融合发展的有力践行,不仅为旅游业的发展提供更多机会,同时将旅游的创新成果深度融合于经济社会各领域之中,提升其他产业的创新力和生产力,形成更广泛的以“旅游+”为先导的各项经济建设新常态。所以我们应当支持这种行业之间的拓展联系。
第三,参考通用标准制定新的投入产出表。由于我国投入产出表的编制起步较晚,所以相对于发达国家较为完善的投入产出编制表来说还存在诸多缺陷。而且我国政府尚未形成一个完整合理的行业分类表,投入产出表中的行业分类与证监会等权威国家机构的行业划分仍有较大差异。本文在研究过程中遇到的最主要问题就是行业分类过于粗广。根据《国民行业分类注释》(2011年版),我国在2012年最细的投入产出表划分为139×139,而美国等国家的投入产出数据已经有四位数的行业了。究其原因,我国的投入产出表存在着明显的部门合并现象。例如,在2007年的投入产出表中,房屋建筑业、土木工程建筑业、建筑装饰和其他建筑业被划分为同一部门;批发和零售业划分为同一个部门;银行、证券和其他金融活动被划分为同一部门。2012年的投入产出表已经有了显著进步,建筑业、银行证券和其他金融细分开来,变成需要分别统计的对象。虽然我国投入产出表尚不完善,但是我们可以看到其逐步改进的迹象。在2017年的投入产出表核算中,希望国家统计局能深入研究联合国统计司推荐采用的《主产品分类》和《全部经济活动的国际标准行业分类》,逐步制定出一个较为规范统一的行业分类办法,并把其广泛应用于各部门行业类统计数据的收集工作中。
责任编辑、校对:郑雅妮endprint