基于双椭球模型的双星系统稳定性研究
蓝磊,杨墨
(清华大学 航天航空学院,北京 100084)
基于双椭球模型的双星系统稳定性研究
蓝磊*,杨墨
(清华大学 航天航空学院,北京 100084)
太阳系中存在着数量众多的双星系统。研究双星系统对于认识小行星的起源和演化有着重要意义。本文以双椭球模型,使用Joshua推导的四阶精度相互势,对双互锁双星系统进行研究。并通过KTC定理证明其稳定性。研究结果验证了卫星和主星存在相对滚转角速度是双互锁系统的一种可能的绕转方式。
双星系统;双互锁;双椭球;稳定性
0 引 言
随着深空探测技术的发展,对小行星的探索越来越引起人们的兴趣。探测小行星对于研究宇宙的起源和太阳系的演化有着重要的意义。在众多近地小行星中,有15% ± 4%的小行星是以双星环绕的模式存在的,在主带中,则有2%的小行星以双星模式存在,可见太阳系中双星系统数量众多[1]。1993年,第一个双星系统Ida-Dactyl被发现,马上吸引了众多科学家的关注[2]。其中,双星系统1996 FG3被选定为欧洲航天局(ESA)MarcoPolo-R任务的探测目标。
目前,人类发现的双星系统可以被简单地分为三类,分别为一般系统、单自锁系统和双互锁系统[6]。一般系统下,主星和卫星在互相绕转平面里的自旋角速度,与其相互环绕的角速度不存在明显的倍数关系。单自锁系统下,卫星在绕转平面里的自旋角速度与两星相互环绕角速度一致,主星的自旋角速度则没有这样的关系,其结果类似于月球对地球的锁定。双互锁系统下,主星和卫星在互相绕转平面里的自旋角速度,与两星相互环绕的角速度保持一致,其结果表现为两小行星的相互朝向保持不变。由于小行星距离地球遥远且相比于大行星来说相对较小,目前人类主要靠雷达或光学成像研究远距离小行星的形状特征,其精度有限,无法准确地获知小行星的具体形状及其周围精确的引力势能分布。使用简单的几何构型对双体小行星进行研究,对于将来探测器前往未探小行星的任务有着重要的指导意义。
Scheeres等基于球–椭球模型对双星系统1999 KW4进行了深入的研究,提出一部分双星系统可能由原始星体裂解而成的理论。Bellerose和Tardivel等基于球–椭球模型对航天器在双星系统中运行时的可行域及轨道转移的方法进行了研究[5]。尚海滨等则使用双椭球模型研究了航天器在双互锁系统下的周期轨道,并提出了其在空间任务中的应用[6]。本文基于双椭球模型,对双互锁系统的可能平衡模式的稳定性进行了研究。
1 研究目标与力学分析
1.1 双星系统的分类及研究对象
正如引言中所说,双星系统根据其自转与相互绕转的速度,可以将其分为3类:即一般系统、单自锁系统和双互锁系统。表 1显示了人类探得的各个系统的代表。其中,D1和D2分别代表主星和卫星在其相互绕转平面上的平均直径;R代表两星质心间的距离;P1和P2分别为主星和卫星在相互绕转平面里的自转周期;Porb则为两星相互绕转的周期。带有括号的数据代表本数据是估计的,或是使用可信度较差的数据,或是数据的获取过程带有一定假设。

表 1 3类双星系统及其代表Table 1 Three categories of binary system
从表 1中D2/D1列可得,单自锁系统两星尺寸相差较大,而双互锁系统两星的尺寸趋近于一致。简单定性分析来说,单自锁系统因为尺寸相差较大,主星对卫星的潮汐锁定等作用较大,卫星对主星的影响则较小。双互锁系统由于两星尺寸相近,所以两星相互影响的量级相近,容易相互作用形成双互锁的系统。
1.2 相互势与力矩
本文以两个刚性椭球体相互绕转的模型来模拟双互锁双星系统的稳定性规律,并使用表 1中的809 Lundia系统作为研究对象。如图 1所示,令Ω代表大椭球,即主星,令Ω'代表小椭球,即卫星。其中,O和O'分别为主星椭球和卫星椭球的质心。为主星固连本体坐标系,为卫星固连本体坐[标系,它们]分别指向椭球的三个惯量主轴,分别与abc相互对应,形成互相正交的坐标系,其中a,b,c分别指了椭球的最长轴,中间轴和最短轴,即a > b > c。定义两物体相互势的表达式为都为体积分。其中dm为椭球Ω中的一个质量微元,dm′为椭球Ω′的一个质量微元。根据Joshua Ashenberg在文章中所推导,两质量微元的倒数可以展成[4]
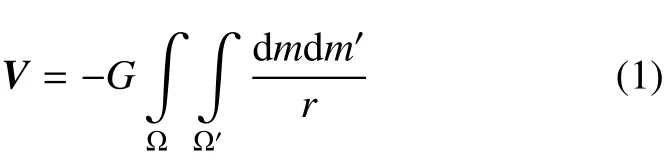

图 1 相互势Fig. 1 Mutual gravitational potential
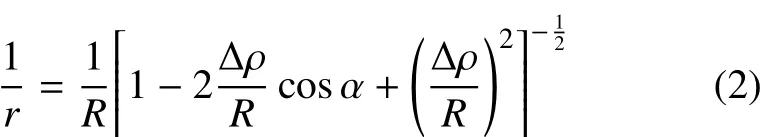
其中:R为两椭球质心间的距离;ρ为主星质心到微元的距离;表示矢量ρ投影到坐标系;所以为椭球Ω′本体坐标系到椭球Ω本体坐标系的转换矩阵。∆ρ=ρ−ρ′,由此可将相互势的表达式通过勒让德多项式展成
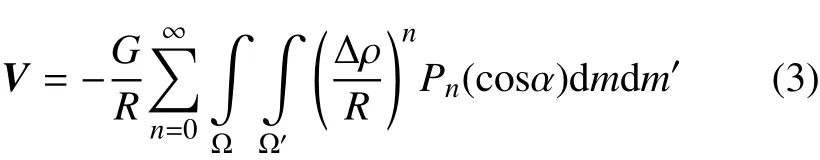
将相互势展到四阶精度,已经基本能够保证精度的需要
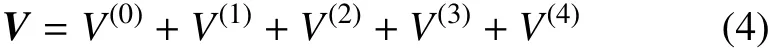
由推导可得,主星椭球体受到的外力矩为
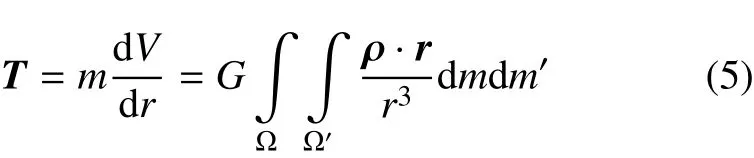
得
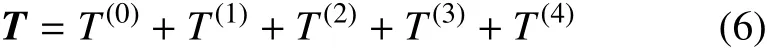
将式(4)所得的四阶精度代入以上方程得椭球情况为
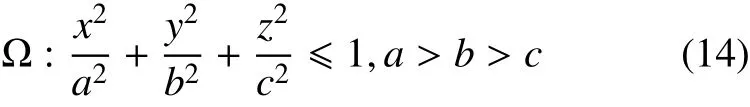
根据以下椭球的坐标变换
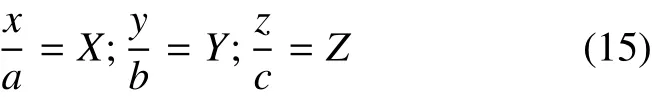
及

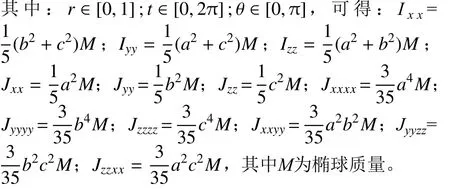
1.3 动态方程及其稳定性分析
本文取卫星Ω′作为研究对象,研究其相对于主星的运动。卫星相对于主星可能存在滚转角速度。假设滚转的角速度如图 2所示。

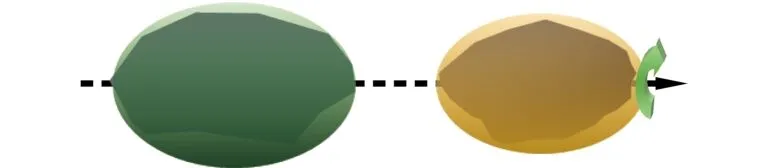
图 2 相对滚转角速度Fig. 2 Relative roll angular velocity
取原点在卫星质心,建立卫星主轴坐标系,可得其相对于主星本体坐标系动力学方程为
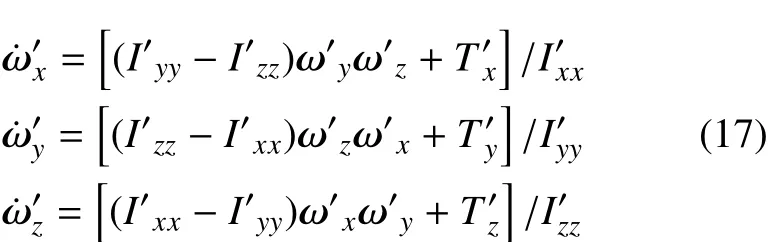
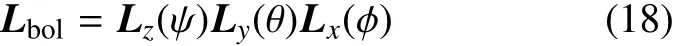
则有欧拉运动学方程
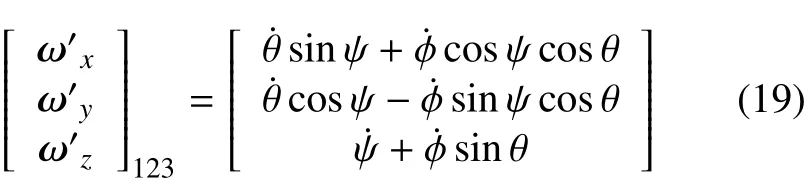
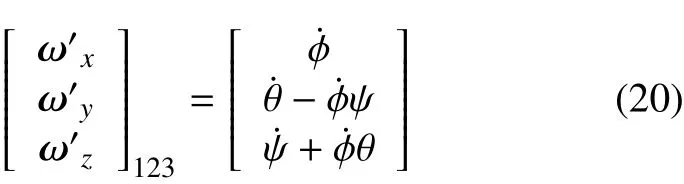
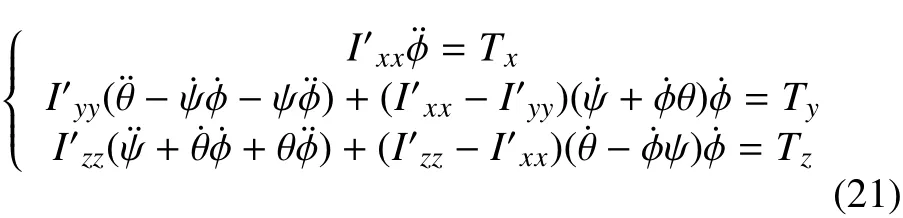
动力学方程有特解为
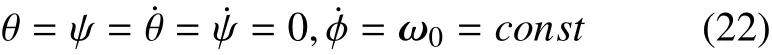
将T也线性化,得
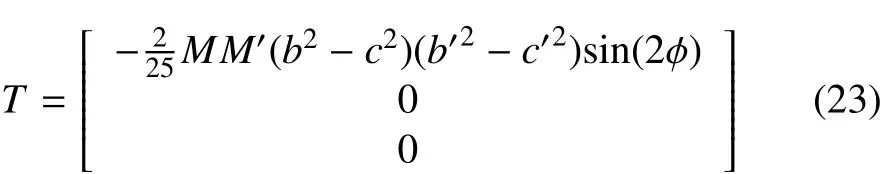
方程变为
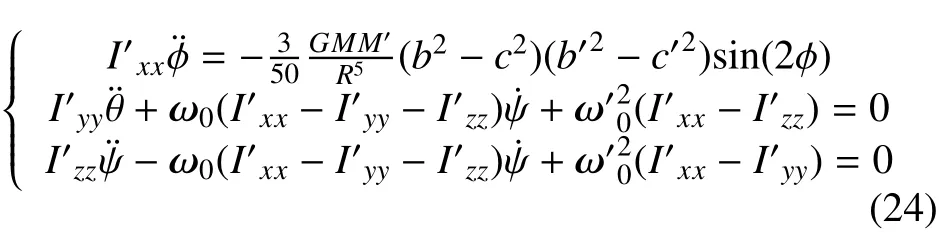
可知ϕ与θ,ψ解耦。分析以下方程
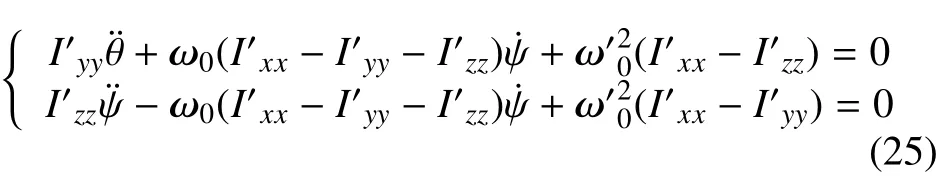

图 3 两种平衡状态Fig. 3 Two kinds of stability
如果令
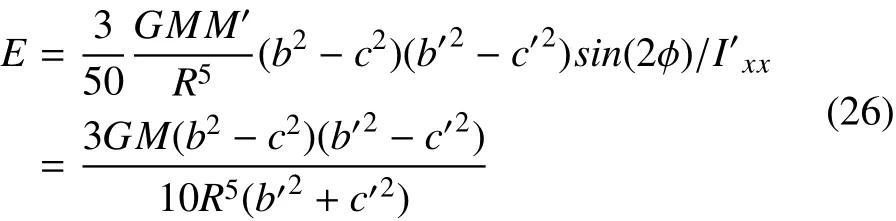
得
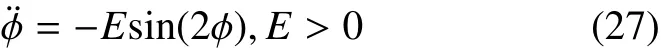
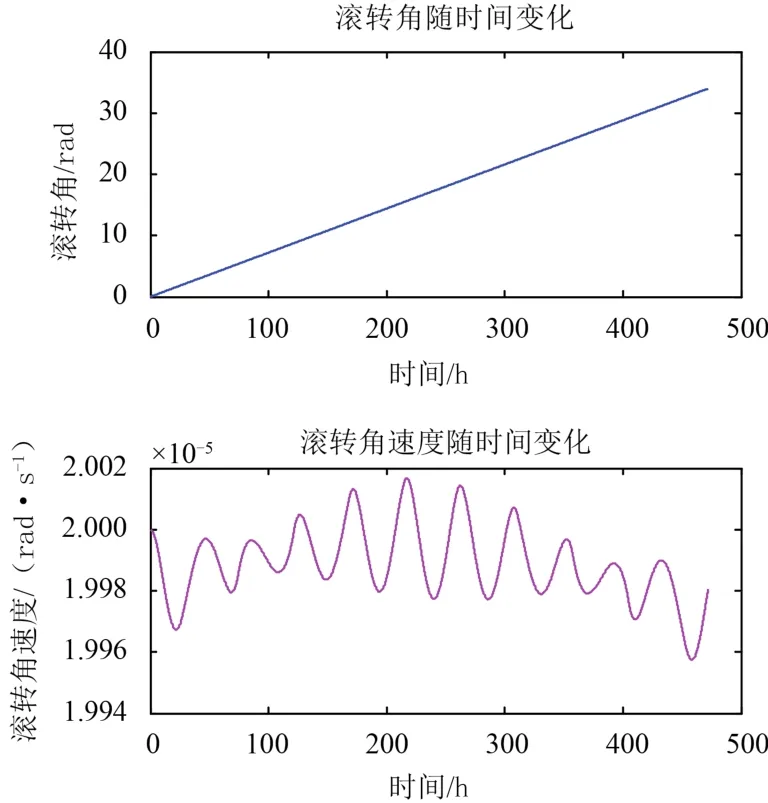
图 4 滚转角和滚转角速度随时间的变化Fig. 4 Roll angle and roll rate change over time
可见滚转角速度在一个很小的范围内震荡,并有衰减的趋势,而滚转角则平稳地增加。相对滚转角速度的衰减可以认为,由于两星的相互作用,使得卫星滚转角速度减小,而主星的滚转角速度增加。两星有趋于同步的趋势。
3 结 论
通过以上分析可得,当双星系统的质量都较小时,它们之间的相互影响是非常微弱的。但在长时间的积累且存在空间能量耗散的情况下,两星有趋于同步的趋势,因此形成了各种自锁的系统。在双互锁系统中,当卫星相对于主星有滚转角速度且滚转轴为最大惯量主轴或者最小惯量主轴时,双星的双互锁规律能够得到保持。这可能是实际双互锁系统存在的一种形式。
[1]Margot J L,Nolan M C,Benner L A M,et al. Binary asteroids in the near-Earth object population[J]. Science,2002,296(5572):1445-1448.
[2]Merline W J,Weidenschilling S J,Durda D D,et al. Asteroids do have satellites[J]. Asteroids III,2002,1:289-312.
[3]Helfenstein P,Veverka J,Thomas P C,et al. Galileo photometry of asteroid 243 Ida[J]. Icarus,1996,120(1):48-65.
[4]Ashenberg J. Mutual gravitational potential and torque of solid bodies via inertia integrals[J]. Celestial Mechanics and Dynamical Astronomy,2007,99(2):149-159.
[5]Tardivel S,Scheeres D J. Ballistic deployment of science packages on binary Asteroids[J]. Journal of Guidance,Control,and Dynamics,2013,36(3):700-709.
[6]Shang H B,Wu X Y,Cui P Y. Periodic orbits in the doubly synchronous binary Asteroid systems and their applications in space missions[J]. Astrophysics and Space Science,2015,355(1):69-87.
[7]Bellerose J,Scheeres D J. Restricted full three-body problem:application to binary system 1999 kw4[J]. Journal of Guidance,Control,and Dynamics,2008,31(1):162-171.
[8]Descamps P. Roche figures of doubly synchronous asteroids[J]. Planetary and Space Science,2008,56(14):1839-1846.
[9]Noll K S,Levison H F,Grundy W M,et al. Discovery of a binary Centaur[J]. Icarus,2006,184(2):611-618.
[10]Bellerose J,Scheeres D J. Dynamics and control for surface exploration of small bodies[C]//Proceedings of AIAA/AAS 2008 Astrodynamics Specialist Conference. [S.l.]:AIAA,2008:18-21.
[11]Tardivel S,Michel P,Scheeres D J. Deployment of a lander on the binary asteroid(175706)1996 fg3,potential target of the european marcopolo-r sample return mission[J]. Acta Astronautica,2013,89:60-70.
[12]Pravec P,Harris A W. Binary asteroid population:1. Angular momentum content[J]. Icarus,2007,190(1):250-259.
通信地址:北京市海淀区清华大学蒙民伟科技大楼北楼N904(100084)
电话:(010)62773402
E-mail:lanl14@mails.tsinghua.edu.cn
Research on a Potential Stability Form of Doubly Synchronous Binary System Based on Triaxial Ellipsoids Model
LAN Lei*,YANG Mo
(School of Aerospace Engineering,Tsinghua University,Beijing 100084,China)
There are numerous binary systems in solar system. The research on binary systems is important for understanding the origin and evolution of asteroids. A two-triaxial-ellipsoid system is used to model the binary asteroids. Combining with Joshua’s research in fourth-order mutual gravitational torque of two bodies, the stability of the binary system is proved by KTC theorem. Thus, the results verify a potential form of the doubly synchronous binary asteroids system where there is a roll angular velocity between the primary and moonlet.
binary system;doubly synchronous;two triaxial ellipsoids;stability
V529.2
A
2095-7777(2017)02-0196-05
10.15982/j.issn.2095-7777.2017.02.015
蓝磊(1992– ),男,博士研究生,主要研究方向:航天器动力学与控制。
[责任编辑:杨晓燕,英文审校:朱鲁青]
蓝磊,杨墨. 基于双椭球模型的双星系统稳定性研究[J]. 深空探测学报,2017,4(2):196-200.
Reference format: Lan L,Yang M. Research on a potential stability form of doubly synchronous binary system based on triaxial ellipsoids model [J]. Journal of Deep Space Exploration,2017,4(2):196-200.
2016-03-01
2016-04-30
国家自然科学基金资助项目(11572166,11372150)

