调整型Bayes序贯验后加权战术导弹批抽检方法
宋贵宝,刘泽坤,罗亚民,李一夫
(海军航空工程学院 a.飞行器工程系; b.研究生管理大队, 山东 烟台 264001)
【装备理论与装备技术】
调整型Bayes序贯验后加权战术导弹批抽检方法
宋贵宝a,刘泽坤b,罗亚民b,李一夫b
(海军航空工程学院 a.飞行器工程系; b.研究生管理大队, 山东 烟台 264001)
针对战术导弹批抽检为连续批、批量小的特点,结合Bayes理论,融入调整型检验的思想,提出了一种基于调整型序贯验后加权检验的战术导弹批抽检方法;该方法结合指标的先验信息,依据比例系数调整双方风险,预先设定3种宽严不同的序贯验后加权抽样检验方案,有效利用历史检验批的抽检结果;算例结果证明:该方法能适用于小子样条件下的战术导弹批抽检。
调整型抽样检验;序贯验后加权检验;战术导弹;连续批
高新技术迅猛发展,推动了战术导弹武器装备的革新,其更新换代速度加快,单枚造价逐渐高昂。针对战术导弹命中概率、命中精度进行的批抽检试验成本很高,人们希望能够在较小的样本量下进行批抽检。因此,应用小子样理论的抽样检验方案逐渐成为战术导弹批抽检试验研究的重点。
0 引言
导弹的批生产品质抽样检验(以下简称“批抽检”)属于可靠性验收试验,且主要是连续批次的提交检验,每批生产数量一般较少(一般在50~200枚)。目前我国战术导弹的批抽检,主要参照GJB179A—1996的调整型抽样检验方案。调整型抽检方案适用于连续批次的抽样检验,并且能有效控制双方风险α和β,但其缺点在于抽检方案样本量较大,费用高耗时长,已不适用于战术导弹的发展趋势。
序贯验后加权检验(Sequential Posterior Odd Test,SPOT)[1]是指能在现场试验中根据试验样本的实际情况实时地进行统计决策。该方法可根据试验参数样本的实际情况进行决策,并且能有效利用先验信息[2-3]。其与一次计数抽样检验方法相结合,可制定直观、简便的抽样检验方案,有效减少样本量,但该方法并不适用于连续批次的抽检。
基于此,本文融合调整型抽样检验和序贯验后加权检验的思想,在结合Bayes理论的基础上,以战术导弹飞行可靠性为指标,提出一种调整型Bayes序贯验后加权战术导弹批抽检方法。该方法有效结合战术导弹生产定型等试验过程中的先验信息,依据比例系数,预先设定3种宽严不同的序贯验后加权检验方案,并建立转移规则进行方案之间的转移。能够有效控制双方风险,减少试验样本量,适用于连续批的抽检。
1 序贯验后加权检验概述
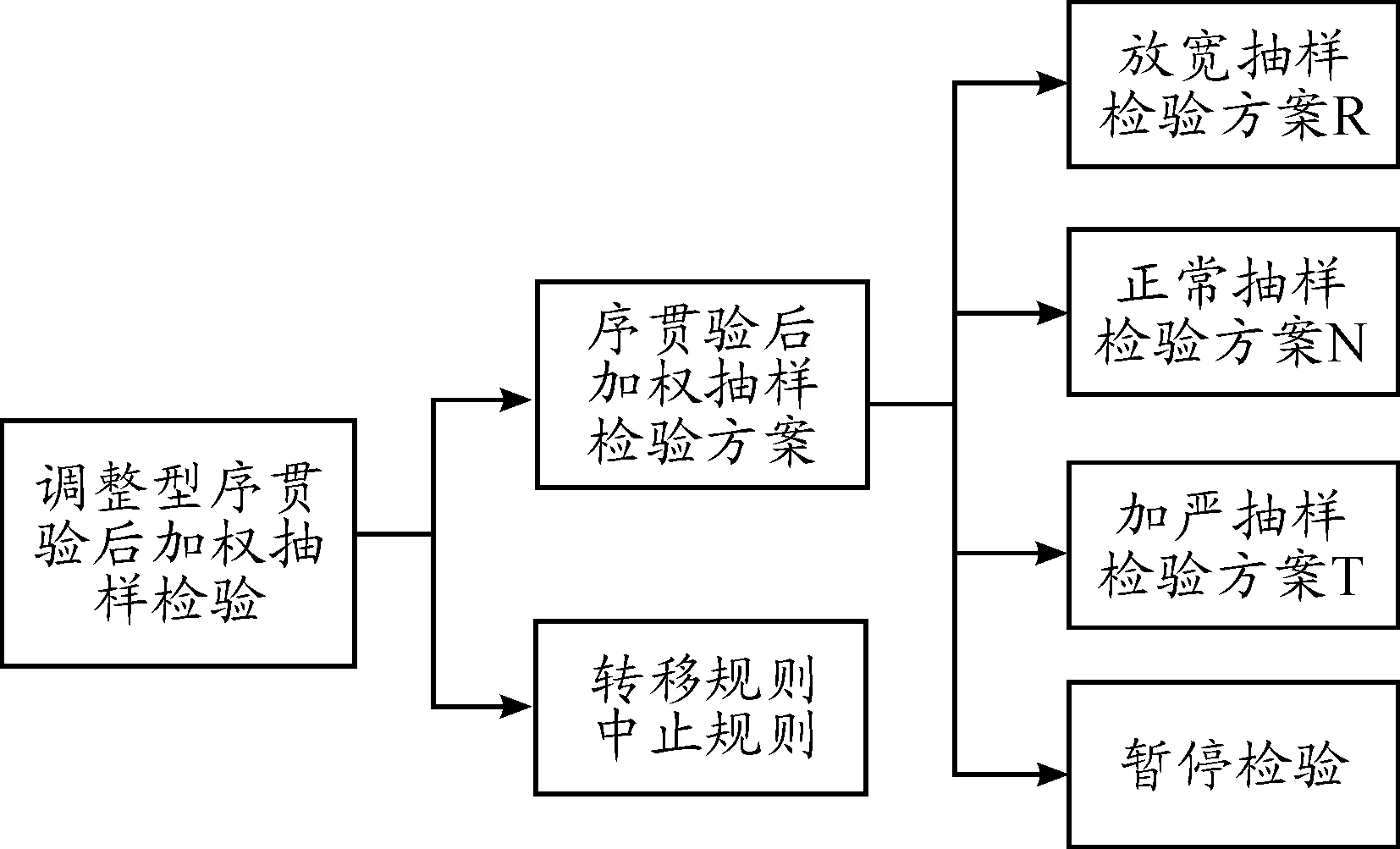
一次计数抽样检验方案,是指从该批次产品中,随机抽取样本量为n的子样本进行检验,根据检验出该子样本不合格产品数d以及合格判定数c判定该批次产品是否合格:当d≥c时,批次合格,用户接收;当d 对于战术导弹批抽检,其可靠性试验数据服从于不合格品率参数为p的(0~1)独立同分布样本,其中,d表示n次试验中的失败次数,且d服从于参数为(n,p)的二项分布,则有: (1) 其中,p的验前密度π(p)采用共轭分布,即β分布Beta(p;απ,βπ)[4],则: (2) 由Bayes理论可知,其验后密度π(p︱d)仍是β分布Beta(α1,β1): (3) 式(3)中,α1=απ+d;β1=βπ+n-d。 设二项总体分布b(n,p)中未知参数p的检验假设为 H0:p≤p0,H1:p≥p1 令Θ0={p:p≤p0},Θ1={p:p≥p1},则Θ0∪Θ1∈Θ,Θ0∩Θ1=φ,Θ为参数空间,p0为产品合格品质水平,p1为产品不合格品质水平。 根据截尾SPOT方法思想[5],犯第1类弃真错误απ0和第2类存伪错误βπ1的概率分别为 ︱H0)dFπ(p) (4) (5) 为了计算上式概率,现计算: P{On>D︱p,p∈Θ0}=1-P{0≤On≤D︱p,p∈Θ0}= (6) 如果记: (7) 可看出,在απ、βπ、n已知情况下,h(d)是关于d的单调不减函数,因此,可得不等式h(d)≤D的解为 d≤h-1(D) (8) 合格判定数c=h-1(D),又已知d~b(n,p),则有: P{0≤On≤D︱p,p∈Θ0}=P{0≤d≤c︱p,p∈Θ0}= (9) 这样,得到犯第1类和第2类错误的概率分别为 ︱H0)]dFπ(θ)= (10) (11) 根据式(10)和式(11)可得,犯第1类弃真错误απ0和第2类存伪错误βπ1只与子样本大小n和合格判定数c有关。因此,在生产方和使用方协商好合格品质水平p0、不合格品质水平p1、生产方风险α和使用方风险β这4个参数的前提下,即可制定抽样检验方案(n,c),且方案必须满足以下条件: (12) 一般来说,由3类宽严程度不同的抽样方案以及转移规则,可以构成一套完整的调整型抽样检验计划。因此,将序贯验后加权检验和调整型抽样检验的思想相结合,并采用GJB179A—1996的转移规则,提出适用于战术导弹批抽检的计数调整型序贯验后加权抽样检验方法,如图1所示。 图1 调整型序贯验后加权抽样检验计划 2.1 正常序贯验后加权抽样检验方案 战术导弹的批抽检,一般遵循风险共担的原则,因此,制定正常方案,一般使双方风险相等,即α=β;正常方案通常包括以下几步: 1) 对该型战术导弹历史生产定型中的试验数据进行收集整理,运用系统可靠性评定方法对数据进行综合,获取该型战术导弹不可靠性p的先验分布Beta(απ,βπ); 2) 给定战术导弹批抽检的可接收品质限p0(AQL)、极限品质限p1(LQ),并经生产方和使用方协商,制定出生产方风险αN、使用方风险βN并满足αN=βN; 3) 依据第2章介绍的计数序贯验后加权检验方案,根据式(10)、式(11),在满足式(12)的条件下,可制定出几组抽样检验方案(n,c),选取样本量n最小的方案,即为正常序贯验后加权检验方案。 当产品品质在p0和p1之间的时候,多数时间是采用正常检验方案N进行抽检。如果产品品质水平发生变化,则应根据变化情况,选取加严或者放宽方案。 2.2 加严序贯验后加权抽样检验方案 当产品品质水平变坏时,应采用加严检验方案T,以此增大生产方风险,保护使用方的利益。本文在设计加严序贯验后加权抽样检验方案时,取生产方风险αT为正常方案下风险αN的λT倍,且λT>1,即αT=λTαN(λT>1 ),同时,要保护生产方利益,即降低生产方风险βT。如图2所示,采用平推法,将正常序贯验后加权抽样检验方案的OC曲线,在p0、p1两点向下平移相同比例距离,即可得到加严的序贯验后加权抽样检验方案。 图2 正常方案与加严方案OC曲线 因此,有: (13) 将αT=λTαN代入式(13),则 (14) 2.3 放宽序贯验后加权抽样检验方案 当产品品质水平变好时,应采用放宽抽样检验方案,适当减小生产方风险αR。取生产方风险αR为正常方案下风险的αN的1/λR倍,且λR>1,即αR=αN/λR(λR>1)。同时,由于产品品质水平较好,可适当放大使用方风险βR。如图3所示,采用平推法,将正常序贯验后加权抽样检验方案的OC曲线,在p0、p1两点向上平移相同比例距离,即可得到放宽的序贯验后加权抽样检验方案。 图3 正常方案与放宽方案OC曲线 因此,有: (15) 将αR=αN/λR代入式(15),则 (16) 2.4 转移规则 如图4所示,GJB179A—1996给出了调整型抽样检验关于正常、加严和放宽3种方案的转移规则[6]。 图4 GJB179A—1996给出的抽样检验方案转移规则 假设对一连续批批量N为100的某型战术导弹进行批抽检,可靠度指标为R0=0.75,设定p0=0.25,p1=0.3;经生产方和使用方协商,双方风险分别为α=20%,β=20%;假设加严方案和放宽方案中λT=λR=1.5,求得加严方案中αT=30%,βT=17.5%;放宽方案中αR=13.3%,βR=21.7%; 对于该型导弹可靠性指标,提出统计假设: H0:p≤p0,H1:p≥p1; 其中,p表示不合格品率。 基于该型导弹生产定型中的大量试验数据,运用系统可靠性评定方法进行综合分析检验,获得该型导弹不合格品率p的先验分布为Beta(4.026 4,8.325 9)。运用建立的抽样检验模型,经过仿真计算,可得以下几组抽样检验方案: 从表1中,综合比较各类方案的双方风险α和β,在已知不合格品率p的先验分布的情况下,可得如下结果: 1) 正常序贯验后加权抽样检验方案,可采用(n,c)为(4,1)的计数抽样方案,即可做出决策; 2) 若在正常检验方案下,出现的不合格批情况满足于正常方案转为加严方案(N→T)的转移规则,则抽检方案转为加严序贯验后加权抽样检验方案。 由表1可知,(n,c)为(5,1)的计数抽样方案,即可做出决策,满足加严风险要求; 3) 若在正常检验方案下,出现的不合格批情况满足于正常方案转为放宽方案(N→R)的转移规则,则抽检方案转为放宽序贯验后加权抽样检验方案。 放宽序贯验后加权抽样检验方案,可采用(n,c)为(7,2) 的计数抽样方案,即可做出决策,且满足放宽风险要求; 进一步通过改进λT、λR的取值,确定大小合适的加严和放宽方案的双方风险值,有利于采取合适的宽严程度不同的抽样检验方案,减少试验样本量。 表1 几组抽样检验方案结果 调整型抽样检验一直是战术导弹批检试验中的重要方法,能有效控制双方风险。但战术导弹的发展趋势对批检试验中所需样本量提出了更严苛的要求,采用Bayes序贯检验方法是解决这一问题的有效途径。本文将Bayes序贯验后加权检验与调整型抽样检验思想相结合,运用GJB179A—1996的方案转移规则,设计出调整型Bayes序贯验后加权批抽检方法,能在有效利用先验信息的基础上,通过调整比例系数调整生产方和使用方风险,制定宽严不同的方案,紧跟抽检产品的品质水平,有利于保护双方利益。通过实例验证,该方法能有效减少试验样本量,适用于连续批、批量小等小子样条件下的战术导弹批抽检试验。 [1] 王国玉,申绪涧,汪连栋.电子系统小子样试验理论方法[M].北京:国防工业出版社,2003. [2] 王雪峥.二项分布下的MSPOT方法研究[J].遥测遥控,2015,36(6):70-75. [3] 张金槐.利用验前信息的一种序贯检验方法——序贯验后加权检验方法[J].国防科学技术大学学报,1999,13(2):1-13. [4] 唐雪梅,张金槐,邵凤昌.武器装备小子样试验分析与评估[M].北京:国防工业出版社,2001. [5] 王志刚,卢军.一种基于先验信息的鱼雷计数抽样检验方法[J].论证与研究,2011(5):28-31. [6] 国防科学技术工业委员会.GJB179A-1996:计数抽样检验程序及表[S].北京:国防科学技术工业委员会军标出版发行部,1996. [7] WILLIS A J.Design of a Modified Sequential Probability Ratio Test (SPRT) for Pipeline Leak Detection[J].Computers and Chemical Engineering,2011,35(1):127-131. [8] 刘薇,黄景德,杨勇.基于连续批信息的制导武器鉴定试验方案及风险分析[J].测试技术学报,2015,29(1):54-57. [9] 王雪峥,韩成哲.可靠性试验中多参数空间复杂假设的SPOT方法研究[J].战术导弹技术,2010(1):56-60. [10]解顺强.调整型抽样方案两参数中止规则的研究[J].统计与决策,2016(10):4-7. [11]GANESAN R,RAO A N V,DAS T K.A Multiscale Bayesian SPRT Approach for Online Process monitoring[J].IEEE Transactions on Semiconductor Manufacturing,2008,21(3):399-412. [12]张兴有,罗华锋.基于调整型的战术导弹批检试验抽样方案设计[J].现代防御技术,2012,40(3):50-52. [13]孙晓峰,赵喜春.导弹试验中序贯检验及序贯截尾检验方案的优化设计[J].战术导弹技术,2011(1):9-16. [14]王瑞臣,徐文焱,李建林.导弹可靠性抽检方案[J].舰船科学技术,2013,35(3):121-124. [15]郭齐胜,罗小明,潘高田.武器装备试验理论与检验方法[M].北京:国防工业出版社,2013. [16]赵永刚,米晓莉.基于可靠性和命中精度的导弹批抽检方法[J].四川兵工学报,2015(8):29-31. (责任编辑 周江川) Sampling Method of Tactics Missile Batch Based on Adjusting Attribute Bayesian Sequential Posterior Odd Test SONG Gui-baoa, LIU Ze-kunb, LUO Ya-minb, LI Yi-fub (a.Department of Vehicle Engineering; b.Postgraduate Management,Naval Aeronautial and Astronautical University, Yantai 264001, China) In the view of the characteristics of continuous sampling of tactical missile batches, combining the Sequential Posterior Odd Test(SPOT) with adjusted attribute sampling inspection, a new sampling inspection method is proposed based on the Bayesian theory. This method combines the prior information of indicators, and adjusts the risk of both parties according to the proportion coefficient, and presets three kinds of sequential and post-weight weighted sampling test programs and makes effective use of sampling results of historical batches. The results of numerical examples show that this method can be applied to batch sampling of tactical missiles under the condition of small samples. sampling inspection based on adjusting attribute; Sequential Posterior Odd Test (SPOT); tactical missile; continuous batch 2017-03-07; 2017-03-29 宋贵宝(1964—),男,教授,主要从事导弹武器系统工程、管理科学与工程研究。 10.11809/scbgxb2017.06.005 format:SONG Gui-bao,LIU Ze-kun,LUO Ya-min, et al.Sampling Method of Tactics Missile Batch Based on Adjusting Attribute Bayesian Sequential Posterior Odd Test[J].Journal of Ordnance Equipment Engineering,2017(6):24-28. TJ760 A 2096-2304(2017)06-0024-05 本文引用格式:宋贵宝,刘泽坤,罗亚民,等.调整型Bayes序贯验后加权战术导弹批抽检方法[J].兵器装备工程学报,2017(6):24-28.



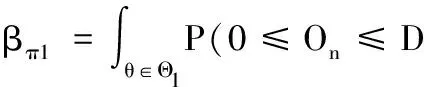
2 适用于连续批抽检的调整型Bayes序贯验后加权抽样检验计划







3 实例分析

4 结束语

