线电荷与接地相切导体圆柱所形成的电场及其可视化

王福谦

（长治学院 电子信息与物理系，山西 长治 046011）

线电荷与接地相切导体圆柱所形成的电场及其可视化

王福谦

（长治学院 电子信息与物理系，山西 长治 046011）

将理论分析与计算机数值模拟相结合，通过保角变换法和镜像法研究线电荷与接地相切导体圆柱所形成的电场，给出其电势分布的解析解，并利用MATLAB软件实现了场分布的可视化。

线电荷；接地相切导体圆柱；保角变换；镜像法；电势分布；可视化

文章运用保角变换法和平面镜像法，讨论了线电荷与接地相切导体圆柱所形成的电场，得出线电荷在圆柱外部空间区域内的电势分布，并利用MATLAB绘制出电场线和等势线（面）图。

1 电势分布函数

如图1所示，在半径分别为R1、R2的无限长的接地相切导体圆柱附近，平行于圆柱体放置有电荷线密度为λ的均匀荷电线，因在垂直于荷电线的所有截面上电场的分布均相同，则所求的电场为平行平面场。取其任一截面为复平面z，以两导体圆柱切点处为原点建立坐标系，荷电线在该复平面上的位置为P（x0，iy0）。为了应用平面镜像法求得线电荷的电场分布，需将z平面上除两相切圆以外的求解区域映射为上半平面，为此先作如下的保角变换[1]。

该变换将z平面上挖去两圆的全平面映射为ζ1平面上宽度为π的带形区域，如图2所示。再通过指数变换：

又将上述带形区域变换到ζ2平面的上半平面，如图3所示。

图1 线电荷与接地相切导体圆柱的横截面

图2 经式（1）变换后的水平带形区域

式（2）可展开为：

图3 经指数变换后的上半平面及线电荷位置

图4 经平移变换后的上半平面及线电荷位置

若要进一步计算线电荷与接地相切导体圆柱所形成电场的场强分布，可由场强与电势的微分关系E=-▽u对式（8）取梯度的负值得到。

2 等势线与电场线函数

因式（7）为线电荷与接地相切导体圆柱所形成电场的复势表达式，故令式（7）中的实部为常数，得

式（9）为线电荷与接地相切导体圆柱所形成电场的等势线函数，且满足（x+R1）2+y2＞R12，（x-R2）2+y2＞R22。

同理，令式（7）中的虚部为常数，即

其中C2为任意常数。式（10）为线电荷与接地相切导体圆柱所形成电场的电场线函数，且满足（x+R1）2+y2＞R12，（x-R2）2+y2＞R22。

3 场分布的可视化实现

为了给出线电荷与接地相切导体圆柱所形成电场分布的直观图像，以验证文章讨论结果的正确性，下面利用软件MATLAB的数值模拟功能[2,3]，对其场分布进行可视化。图5-8为利用MATLAB所绘制的线电荷与接地相切导体圆柱所形成的电场的电场线和等势线（面）图（其中取λ/2πε0的量值为15）。图中的电场线与等势线及导体圆柱面均垂直，零值等势线与接地导体的边界重合（注意：电势的取值为contour（x,y,U,[0,0.25:2.5:50]），0V等势线与导体边界重合，最靠近导体表面的蓝色等势线的电势为0.25V），图线分布正确，为预期结果，这说明文章研究方法正确，结论可靠。

图5 线电荷与接地相切导体圆柱所形成的电场（R1=2m，R2=3m；xn=0、yn=-12m）

图6 线电荷与接地相切导体圆柱所形成的电场（R1=6m，R2=1m；x0=2m、y0=10m）

图7 线电荷与接地相切导体圆柱所形成的电场（R1=2m，R2=3m；xn=0、yn=-12m）

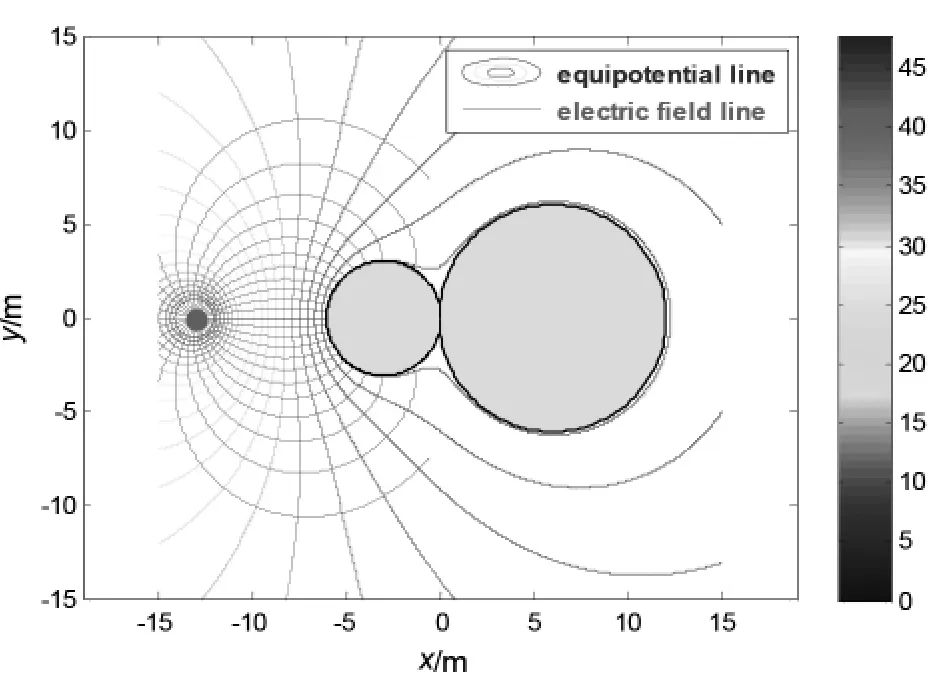
图8 线电荷与接地相切导体圆柱所形成的电场（R1=3m，R2=6m；x0=-13m、y0=0）

4 结束语

文章将理论分析与计算机数值模拟相结合，研究了线电荷与接地相切导体圆柱所形成的电场，给出其电势分布的解析解，并利用MATLAB软件实现了场分布的可视化，为边界复杂的静电场边值问题的求解提供了一种思路与方法，可供电线电缆中相关问题的研究借鉴和参考。

［1］曹伟杰.保形变换理论及其应用［M］.上海：上海科学技术文献出版社，1998.54-55.

［2］张德丰，雷小平.详解MATLAB图形绘制技术［M］.北京：电子工业出版社，2010.57-93.

［3］周群益，侯兆阳，刘让苏.MATLAB可视化大学物理学［M］.北京：清华大学出版社，2010.329-340.

The Electric Field of a Line Charged and a Grounding Tangent Conductor Cylinder and Its Visualization

Wang Fu-qian
（Department of Electronic Information and Physics Changzhi University,Changzhi Shanxi 046011）

By combing theoretical analysis with Computer Simulation,the electric field of a line charged and a grounding tangent conductor cylinder is studied by using the conformal mapping method and plane mirror method.Its analytical solution of electric potential distribution is obtained,and the electric field distribution is visualized by using the software MATLAB.

a line charged;a grounding tangent conductor cylinder;conformal mapping method;plane mirror method;electric potential distribution;visualization

O44

A

1673-2014（2017）02-0001-05

（责任编辑 郝瑞宇）

2017—01—06

王福谦（1957— ），男，山西临猗人，教授，主要从事电磁场边值问题及场结构数值模拟研究。