基于国民生产总值增长率微调制的国家能源年度消费总量Logistic修正模型研究

杨 波，郭剑川,谭章禄

(1.中国矿业大学(北京)管理学院，北京 100083；2.中国科学院国家空间科学中心,北京 100190)



基于国民生产总值增长率微调制的国家能源年度消费总量Logistic修正模型研究

杨 波1，郭剑川2,谭章禄1

(1.中国矿业大学(北京)管理学院，北京 100083；2.中国科学院国家空间科学中心,北京 100190)

本文在国家能源消费Logistic经典解析法模型的基础上，引入国民生产总值(GDP)增长率作为能源消费变化的影响因子之一，建立了基于国民生产总值增长率微调制的国家能源年度消费总量Logistic修正模型。通过美国能源消费历史数据实证分析和检验表明，该修正模型的拟合数据和预测数据与实际结果具有较好的一致性。

能源消费；Logistic模型；GDP；微调制

1 引言

能源是国民经济发展的支柱，是人类赖以生存的物质基础。随着世界各国对能源需求的增长，能源争夺态势正在加强。各国根据各自国情，综合考虑本国经济发展状况和能源储备、能耗效率、未来能源需求预测、环境条件制约等因素，采取相应的对策和措施，力求缓和能源问题。其中，在掌握目前国内外能源资源和能源需求信息之外，科学预测本国国家能源年度消费(即能源需求)的发展趋势、及时掌握世界主要国家的国家能源消费，是科学制定国家能源政策的前提条件，显得尤为重要。

国家能源年度消费总量预测研究已经成为能源研究的重要领域。预测方法和模型也有多种。时间序列方法[1]是以预测对象时间序列的历史数据为基础，通过数据间的内在变化规律建立能源消费与经济增长之间的长期均衡关系和短期均衡关系。典型模型有ARIMA模型[2-4]、GM(1,1)[3,5-6]、神经网络[7-9]和组合模型等[10-12]。另一种研究方法是从基本经济学原理出发，建立能源消费唯象模型，再通过实际数据进行拟合分析和验证。典型的模型是Logistic模型。付娟等人[13]用基于遗传算法的Logistic模型解决了中国清洁能源需求的预测问题。杨波和谭章禄[14]基于Logistic模型建立了中国能源年度消费总量预测模型。

从上述研究成果来看，经过优化后的Logistic经典模型[14]较好地拟合了能源消费的长期增长趋势，具有一定的历史复现能力和中短期预测能力。但是，各国实际的能源年度消费总量曲线大多是波动曲线，而非Logistic经典模型[14]模拟计算得到的平滑曲线。准确研究波动现象的波动机理，并依此修正Logistic经典模型，势必会提高该方法的拟合效果和预测能力。

本文在经典Logistic经典模型[14]的基础上，考虑国民生产总值(GDP)对能源消费的影响，通过引入GDP增长率作为变量之一，建立国家能源年度消费总量Logistic修正模型，具体包括三种不同的衍生数学模型，分别为：Logistic修正解析法模型、Logistic修正动态差分法模型和Logistic修正静态差分法模型。并采用美国1980年～2010年的能源消费历史数据实证检验了Logistic修正模型的拟合效果和预测能力。

2 修正模型的建立和求解

2.1修正模型建立

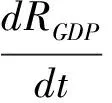
那么在国家能源年度消费总量Logistic经典模型的基础上[14]，考虑国内生产总值增长率变化后的Logistic修正模型表示如下：

(1)

2.2修正模型解析法求解

对方程(1)进行数学变换，

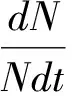
(2)

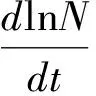
(3)

两边积分得到，

(4)

得到方程的通解为：

(5)

通常情况下，各国的国民经济增长率变化量非常小，一般处于(-0.1，0.1)区间，基本在±0.05之间。α一般处于(0，1)区间。根据微积分原理，对exp(αΔRGDP)进行泰勒级数展开，

exp(αΔRGDP)=1+αΔRGDP+o(αΔRGDP)

一级近似可认为：exp(αΔRGDP)≈1+αΔRGDP

(6)

把公式(6)代入公式(5)，国家能源年度消费的表达式变为：

(7)

其解为：

(8)

从方程解析表达式(8)可以看出，考虑国民经济影响之后的国家能源年度消费总量修正解析函数是在Logistic经典解析函数之上，微调制了GDP增长率的变化。相对于Logistic经典模型，公式(8)对应的数学模型称之为Logistic修正解析法模型(简称为修正解析法模型)。当GDP保持稳定增长时，即GDP增长率的变化为零时，ΔRGDP=0时，带GDP增长率变化量的修正解析法模型就退化为Logistic经典模型。

当选取国家能源年度消费总量的历史统计样本数据为{Nt：t=1, 2, …,n}时，给定时间t的修正解析法模型的拟合相对误差为：

(9)

那么，该模型的均方误差为：

(10)

2.2差分法求解

从前述可以得知，GDP增长率变化量引起的国家能源年度消费总量波动相对来说很小，并不影响国家能源消费曲线的总体走势。因此，可以采用Logistic经典模型拟合得到其国家能源年度消费的固有增长率r和饱和极限值Κ，然后将公式(1)离散化，得到差分方程如下：

(9)

通过逐次迭代可以数值计算得到各个年份的国家能源年度消费总量值。如果只使用N序列的第一期(基准年)的实际观测样本值N0，其后各期能源消费总量值都采用递推方法获得，称之为Logistic修正动态差分法模型，简称动态差分法模型，适合于中长期预测(2年期以上)和总体发展态势分析。与之相对应的是，静态差分法模型采用N序列滞后一期的实际观测样本值N(i-1)来计算当期能源消费总量值N(i)，适用于短期预测(1年期)。很显然，静态差分法模型数值计算结果的精度和有效性都要明显优于动态差分法模型。

数学上可以证明解析法和差分求解法得到的数值模拟结果基本相同。本章在第3部分的数值模拟结果也证明两者结果等价。

3 模型实证分析与检验

3.1数据收集及预处理

美国经济经过二战后30多年的发展，在进入上个世纪80年代后步入稳步发展阶段。从1980年～2010年之间，美国先后经历了第二次中东战争、伊拉克战争、亚洲经济危机、第二次伊拉克战争、阿富汗战争、美国次贷危机和欧洲主权债务危机等重要事件，相应的美国经济在增长过程中也发生了多次波动，甚至是剧烈抖动，这从美国GDP年增长率的波动曲线可以明显看出(如图1所示)。同时期的美国国家能源年度消费总量在总体增长的情况，也出现了同期的波动态势。这也充分说明能源消费与GDP之间的关系的确非常密切。

因此，本文的实证研究选取1980年～2010年的美国能源年度消费总量及其对应的实际GDP增长率数据[15]，相关数据摘录于表1。

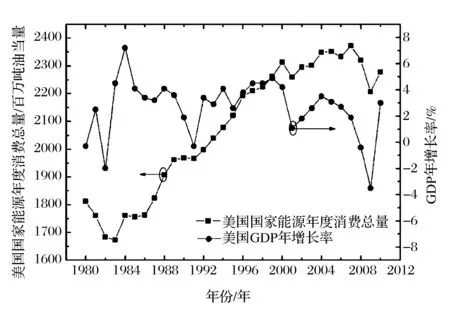
图1 美国国家能源消费总量和GDP增长率历史统计曲线图(1980年～2010年)

3.2数值模拟结果分析

3.2.1 解析法数值模拟结果分析

图2主体部分是基于1980年～2010年美国能源年度消费总量历史数据，采用修正解析法模型模拟计算得到的拟合曲线。为便于比较和查阅，图2中同时给出了2011年和2012年的真实统计样本值和数值计算预测值。从图2中可以看出，修正解析法模型较好地模拟了美国1980年～2010年前后30年的能源年度消费总量，与历史数据吻合度较高。并且相对Logistic经典模型，虽然其预测误差(如表2所示)没有明显减小，但是拟合曲线与历史统计曲线的变化趋势更加相符。这说明修正解析法模型具有较强的历史样本数据再现能力。

图2 美国国家能源年度消费总量Logistic经典模型、修正解析法模型模拟结果与历史统计曲线对比图(1980～2012)

同时，也可以从图2中看到两个非常明显的异常现象。一个是，相对于历史统计样本值，修正解析法模型在1983年、1992年、2010年的拟合曲线波动要大得多。另外一个是，三个波动年份(1983～1984，1992～1993，2011～2012)显示出与历史数据反向变动趋势。经过分析，可以得知，这两个现象的形成机理是一致的，主要与这三年的GDP变化率密切有关。三个波动年份及其前两年的美国GDP都经历了“正-负-正”深V型波动，变化量分别达到了6.5%、3.7%、6.5%。GDP的剧烈波动，势必带来能源需求量的显著变化。公式(6)在数学上近似省去了高阶小项，引入了部分误差。不过，通过计算可以得知，这部分误差占比非常小，可以忽略。另外一个主要原因是能源供需的动态平衡过程。真实世界的市场资源调配是多因素综合的结果，变化速度明显趋缓和滞后。而数学模型因为考虑因素较为单一反应会显得更为激烈，增长量更大，并且更加超前，三个波动年份尤其突出。当然，随后的年份，数学模型“激烈”和“超前”的特性，也势必会将之前拟合过度的数值以更显著的减少量和下降速度给调和回来，从而保持拟合精度的总体优化。GDP变化率较大的对应发展阶段，通常都是经济“W”波动的第一个短暂“V”型复苏阶段。而在第一个“V”型下降期，实际能源消费总量低于理论计算值，也低于实际能源开采量。这部分累积的剩余能源量对随后年份(1-3年)的“V”型上升阶段具有明显的补充调剂作用，从而降低了复苏阶段的能源消费总量。这种裕量释放过程主要集中在第一个“V”型阶段。因此，其调剂作用对“W”波动的第二个“V”型阶段的影响已经非常小。这从第二个“V”型阶段模拟曲线和历史统计曲线间的拟合程度可以得到证实。一般情况下，经历了第二个“V”型阶段后，能源年度消费总量的实际发展趋势又会恢复到经典模型曲线上。

表1 美国能源年度消费总量和GDP增长率数据表(1980年～2010年)

注：Y，年份；N(Y)，Y年份对应的美国国家能源年度消费总量；Mtoe，百万吨油当量。

表2 不同模型计算的美国国家能源年度消费总量相对误差数据对比表(1980～2012)

注：Y，年份；δ1，经典模型对应的相对误差；δ2，修正解析法模型对应的相对误差；δ3，动态差分法模型对应的相对误差；δ4，静态差分法模型对应的相对误差。

采用修正解析法模型计算，2011年和2012年的预测值分别为2383.5Mtoe和2437.5Mtoe。而实际能源消费值分别为2269.3Mtoe和2208.8Mtoe。对应的预测误差分别为5.03%和10.35%。这说明本文建立的修正解析法模型具有一定的预测精度，但是与历史(1980～2010年)数据拟合精度相比，预测误差还是有一些偏大。这与1980～1986年的模拟结果具有极强的相似性。这从另外一个方面也可以说明，美国能源消费可能会在未来3～5年内步入“W”波动的第二个“V”型快速上升阶段，也预示着美国经济和世界经济地逐步复苏。

3.2.2 转换系数α的影响

能源和经济间的因果关系一直是计量经济学模型的研究热点。特别是近20年，许多研究团队和学者采用Granger因果关系检验对实际各国的不同发展历史时期的两者关系进行了广泛深入的研究[16-21]。但是，研究结果存在差异，研究结论还未统一。本文认为能源消费在整个国民经济发展过程中有其自身发展的内在规律，经济变化对能源消费变化有一定影响。公式(1)中引入的转换系数α表征了经济变化对能源消费变化的作用强度。一般情况下，能源消费变化与经济变化之间是正相关的，即α为非负数。

不同α取值下的美国能源年度消费总量拟合曲线如图3所示。从图3中我们看出，当α取非负数(0～1)时，能源消费的确与GDP具有同样的波动趋势。这说明了能源消费变化与经济变化之间的确正相关。当α=0时，经济变化对能源消费变化无影响，修正解析法模型退化为Logistic经典模型。随着α的增大，经济变化对能源消费变化的影响逐渐增强，拟合曲线波动愈加明显。

根据公式(10)，不同α值{0, 0.2, 0.4, 0.6, 0.8, 1.0}时的均方误差σ为{0.0338, 0.0344, 0.0357, 0.0377, 0.0402, 0.0432}。比较不同α值的均方误差σ可以发现：①不同α值对应的均方误差σ相差非常小，拟合结果具有等价性，这与修正解析法的微调制原理是相符的，即修正解析法只是微调制了GDP增长率变化带来的影响，对消费总量影响不大；②α=0时的均方误差σ最小，表明公式(8)所建立修正解析方并不能提高拟合优度，这是由于公式(8)中的关键拟合参数K和r都是直接取之于经典模型[14](此时α=0)的优化拟合数值。

综合来看，修正解析法模型在选取不同α值时与Logistic经典模型在拟合优度上依然具有等价性，但是修正解析法模型可以更好地复现实际能源消费曲线的波动态势，显性表征了能源消费变化与经济变化之间的相关性，对准确预测未来能源消费走势具有一定的积极作用。在模型实际使用过程中，α一般在(0.2, 0.6)区间取值，并且需要根据实际经济发展情况灵活选择。当经济发展较为平稳的时期，α宜选取中间数值。当经济出现快速下滑时，α宜选取较大数值。当经济反弹时，特别是GDP开始出现由负到正的过程时，α宜选取较小数值。

3.2.3 差分法数值模拟结果分析

(1)动态差分法

图4主体部分是基于1980年～2010年美国能源年度消费总量历史数据，采用修正解析法模型和和动态差分法模型模拟计算得到的拟合曲线。与图2相同，为便于比较和查阅，图4中同时给出了2011年和2012年的真实统计样本值和数值计算预测值。

从图4中首先可以看出，修正解析法模型和动态差分法模型得到的拟合结果总体上相近，差别不大。两种计算方法在误差范围内具有等价性。

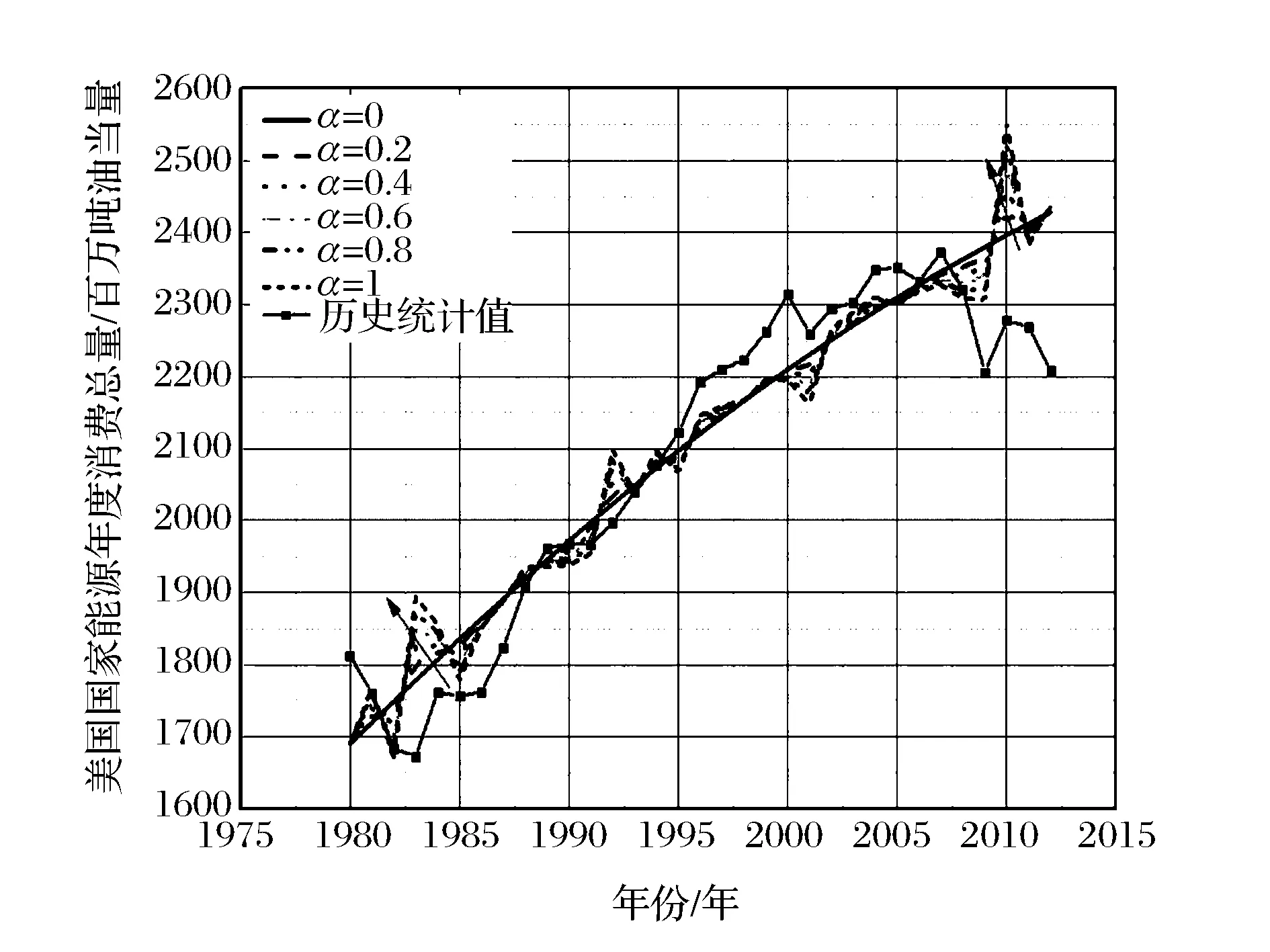
图4 修正模型解析法模型和动态差分法模型计算结果对比图(α=1)

从图4我们还可以看到，动态差分法的拟合曲线在美国经济平稳发展期(1991年～2008年)的拟合精度非常之高，拟合误差基本处于3%以内(如表2所示)，比Logistic经典模型和修正解析法模型的拟合优度要高得多。这说明动态差分法模型具有较强的中长期(2年以上)预测能力。

(2)静态差分法

如图5所示，相对于动态差分法模型，静态差分法模型拟合精度较高。静态差分法模型误差基本控制在4%以内，如表2所示。采用静态差分法模型计算得到的2011年和2012年的美国能源年度消费总量预测值分别为2283.7Mtoe和2293.6Mtoe。预测误差分别为0.63%和3.84%。这说明静态差分法短期预测能力非常好。

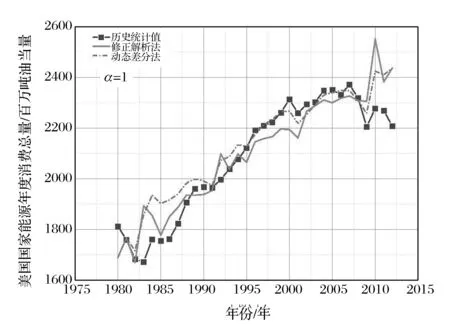
图5 静态差分法模型和动态差分法模型计算结果对比图(α=1)

4 结语

本文在国家能源消费Logistic经典模型的基础上，引入GDP增长率作为能源消费变化的影响因子之一，建立基于国民生产总值增长率微调制的国家能源年度消费总量Logistic修正模型，包括修正解析法、动态差分法和静态差分法三种数学模型。通过采用美国能源消费历史数据实证分析可以得知以下结论：

1)Logistic修正解析法模型具有较强的历史再现能力；

2)Logistic修正模型总体上具有与Logistic经典模型等价相当的拟合能力，特别是静态差分法模型具有较高的拟合精度。

3)国家能源年度消费总量中长期发展趋势有其自身发展规律，主要决定于固有增长率和自然环境条件(即资源禀赋)；

4)Logistic修正模型表现了实际能源能源消费年度总量曲线丰富的波动态势，显性表征了能源消费变化与经济变化之间的相关性；

5)国家能源年度消费总量与国民经济具有正相关性，可以通过GDP增长率的变化量来表征；

6)具有影响力的局部战争和经济危机等众多社会和经济因素对国民经济具有直接的影响，并且可以对国家能源年度消费总量产生一定的间接影响，可以认为是对国家能源年度消费总量自身发展规律的微量调制，从而使国家能源年度消费总量曲线产生短期的“V型”波动。

[1] 李子奈，潘文卿. 计量经济学[M]. 第3版. 北京:高等教育出版社，2010.

[2] 杨伟传. 中国能源消费的ARIMA模型预测分析[J]. 统计与决策，2009,(11)：71-72.

[3] Yuana Chaoqing, Liu Sifeng, Fang Zhigeng. Comparison of China's primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM(1,1) model[J]. Energy, 2016, 100: 384-390.

[4] Ediger V S, Akar S. ARIMA forcasting of primary energy demand by fuel in Turkey[J]. Energy Policy, 2007, 35(3): 1701-1708.

[5] 孙李红，张瑜，焦艳会. 中国能源消费预测的GM(1,1)模型研究[J]. 商业经济，2015,(9):48-49.

[6] 花玲，谢乃明. 政策冲击影响下中国能源消费预测分析及控制策略[J]. 中国管理科学，2014，22(7): 18-25.

[7] Murat Y S, Ceylan H. Use of artificial neural networks for transport energy demad modeling[J]. Energy Policy, 2006, 34(17): 3165-3172.

[8] 王珏，鲍勤. 基于小波神经网络的中国能源需求预测模型[J]. 系统科学与数学. 2009，29(11):1542-1551.

[9] 张俊深，袁程炜. 基于BP神经网络与修正GM(1,1)模型的能源消费组合预测. 统计与决策，2016，(5):90-93.

[10] 卢奇，顾培亮，邱世明. 组合预测模型在我国能源消费系统的构建即应用[J]. 系统工程理论与实践, 2003(3):24-30.

[11] 卢二坡. 组合模型在我国能源需求中的应用[J]. 数理统计与管理, 2006, 25(5):505-510.

[12] 曾波，刘思峰，方志耕，等. 灰色组合预测模型及其应用[J]. 中国管理科学, 2009, 17(5):150-155.

[13] 付娟，金菊良，魏一鸣，等. 基于遗传算法的中国情结能源需求Logistic预测模型[J]. 水电能源科学，2010，28(9):175-178.

[14] 杨波，谭章禄. 基于Logistic模型的中国国家能源消费总量预测研究[J]. 科技管理研究, 2013，33(12):45-48.

[15] U.S. Energy Information Administration (EIA). Annual energy review[EB/DL]. Http://www.eia.gov/totalenergy/data/annual.

[16] Stern D I. A multivariate cointegration analysis of the role of energy in the US macroeconomy[J]. Energy Economics, 2000, 22 (2):267-83.

[17] Huang B N, Hwang M J, Yang C W. Causal relationship between energy consumption and GDP growth revised: A dynamic panel data approach[J]. Ecological Economics, 2008, 67 (1): 41-54.

[18] Kraft J, Kraft A. On the relationship between energy and GNP[J]. The Journal of Energy and Development, 1978, 3 (2):401-403.

[19] Sharma A, Bruce C. The relationship between energy and U.S. GDP:A multivariate vector error-correction model[J]. The Journal of Energy and Development, 2013, 38(1):45-64.

[20] Tiwari A K. The asymmetric Granger-causality analysis between energy consumption and income in the United States[J]. Renewable & Sustainable Energy Reviews, 2014, 36:362-369.

[21] 张优智，党兴华. 能源消费结构与经济增长的动态关联分析[J]. 中国管理科学，2014,22(SI)：840-845.

Research on Adjusted Logistic Model of National Energy Consumption with Slight Modulation by the Growth Ratio of GDP

YANGBo1,GUOJian-chuan2,TANZhang-lu1

(1.China University of Mining & Technology, Beijing, Beijing 100083, China; 2.National Space Science Center, China Academy of Sciences, Beijing, 100190, China)

Energy resources are the base of nationaleconomic development and the essentials of human daily life. As the demands of all countries in the world on the energy resources increase, the competition for the energy resources are becoming more and more intensive. It is vital to collect and analysis the energy consumption data of the major countries around the world so that the government could make correct decision on the future national energy consumption using a scientific prediction model. Not similar to the time series commonly used, an adjusted Logistic model, which is based on the classical Logistic model of national energy annual consumption, is founded in this paper by introduceing a factor of the GDP growth ratio The adjusted Logistic model can be considered as a result of the classical logistic model modulated with the GDP growth ratio. Three different numerical models derived from the original adjusted Logistic model are the adjusted analytic model, dynamic differential model and static differential model. Then, the study and verification, which are based on the real statistic data of the energy annual consumption of USA from 1980 to 2010, shows that the fitted and prediction data are in good agreement with the empirical results. The simulation curve is fitted very well with the energy consumption fluctuation. According to the simulation and analysis results in this paper, a positive relevance between the national energy annual consumption and the national economics are shown directive in the analytic model. The relative prediction errors on 2011 and 2012 using the static differential model are only 0.63% and 3.84%, respectively.

energy consumption; logistic model;GDP; slight modulation

1003-207(2017)06-0032-07

10.16381/j.cnki.issn1003-207x.2017.06.004

2015-04-17；

：2016-11-02

杨波(1978—)，女(汉族)，天津人，中国矿业大学(北京)管理学院，博士生，研究方向：可再生能源路径选择，E-mail:yangbolg@hotmail.com.

F206

：A