基于GA—BP神经网络的耕地自然质量计算模型研究
杭艳红+杨林
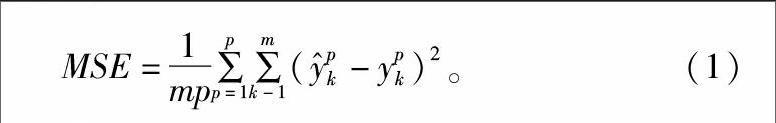
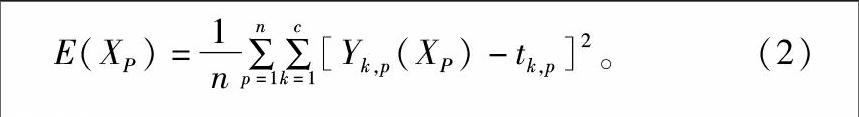
摘要:在常规耕地分等的方法中由于人为因素会干扰评价因子的权重及BP神经网络模型自身优化过程中容易陷入局部极小值的情况,通过遗传算法全局搜索最优权值的能力对BP神经网络进行优化,建立耕地自然质量计算的遗传算法优化的BP神经网络模型(GA-BP网络模型)。以黑龙江省绥化市明水縣进行实证研究,结果证明,GA-BP网络模型能有效地避免常规方法评价因子确定权重时的人为干扰,同时具有较高的优化效率及泛化能力,能够更加快速智能地计算耕地的自然质量分,从而确定耕地的自然等别,应用效果相对较好。
关键词:耕地自然质量;遗传算法;BP神经网络
中图分类号: F323.211文献标志码: A文章编号:1002-1302(2017)08-0183-04
耕地是土地中的精华[1]。中国是农业大国,“十分珍惜和合理利用每一寸土地,切实保护耕地”是我国的基本国策。耕地质量优劣直接决定我国农业发展水平,也是粮食产量的重要保障,耕地质量直接影响农业产业结构和耕地产出水平,耕地质量目前已愈发受到重视,要切实加强耕地质量的评价与监测,从而有效提升耕地内在质量[2]。实现“藏粮于地”已成我国对耕地质量保护与提升的重要目标。耕地红线不仅是数量上的,更是质量上的,要坚持数量与质量并重,为国家农业发展打下坚实基础。人多地少的国情使我国农业生产一直坚持高投入、高产出模式,耕地长期高强度、超负荷利用,造成质量状况堪忧、基础地力下降[3]。耕地质量评价是促进粮食和农业可持续发展的迫切需要和理论基础。了解和摸清土壤资源,开展耕地质量评价,是实现农业可持续发展、确保粮食安全的基础工作[4]。明水县作为黑龙江省主要的农业县,拥有丰富的耕地资源,耕地资源的质量对明水县粮食安全、农产品竞争力、农业结构战略性的调整起到了重要作用[5]。为了科学地研究耕地质量问题,许多专家在模型与方法上进行了深入研究。唐南奇等通过BP神经网络模型和精度检测的方法,通过少量典型样本的训练和学习后,可简便、快捷地计算出大规模待定样本的分等综合指数;其泛化功效和精度检测也符合要求[6];孔维娜认为人工神经网络模型评价方法同样能在耕地评价中达到较高的准确度[7];员学峰建立陕西年耕地面积减少时间序列的预测模型,BP神经网络在对陕西的耕地资源年减少量进行预测时,精度较高、可靠性较好,表明BP神经网络用于耕地减少的预报具有一定的可行性[8]。人工神经网络和遗传算法(GA)的结合应用取得了较多成果。迟宝明通过对比分析结果得出,基于遗传算法的BP神经网络模型对地下水位进行的短期预测明显优于BP神经网络模型,是一种比较理想的短期预测模型[9];张保祥等利用神经网络和遗传算法对济南市市区地下水进行了预报研究,并对地下水位、最大开采量和泉排量进行了预测,效果良好[10]。张学喜利用遗传算法和BP神经网络可以建立边坡稳定性影响因素和边坡稳定性状态之间的非线性映射关系,利用这种映射关系可以评价边坡的稳定状态,而且评价结果具有较高的精度[11]。而在土地评价方面,伍振军基于遥感和遗传BP神经网络算法对流域土地覆盖/土地利用分类方法进行了研究,遗传算法优化的BP神经网络可克服本身缺陷,能够快速提高土地分类的精度[12]。综上得出,BP神经网络存在收敛速度过慢甚至不收敛、容易陷入局部极小值等缺陷。本研究以明水县为例建立了明水县耕地质量评价的体系,利用遗传算法改进的BP人工神经网络对明水县的耕地质量进行更加科学的评价,这些成果为全面提高明水县的农业生产水平,实现耕地质量计算机的动态监管,适时为明水县各个耕地管理单元的耕地质量状况和调节提高的措施提供了基础数据管理平台和数据。在目前农用地分等应用中,耕地质量分等大部分采用相对成熟的《农用地分等规程》中的方法,引入智能化、信息化技术研究耕地自然质量计算的方法相对较少。将遗传算法与BP神经网络有机结合,可实现优势互补,从而达到提高BP神经网络模型整体性能的目的。
1BP神经网络的构建
BP神经网络的实质是求取整个网络总误差函数最小值的问题,具体采用最速下降法按照误差函数的负梯度方向进行权系数修正[13]。BP神经网络具有很强的非线性拟合能力,同时拥有学习规则简单、计算机上容易实现等优点。在BP神经网络中,样本数据从输入层经过隐含层逐层向后传播,训练网络权值则沿着减少误差的方向传递,从输出层经过中间各层逐层向前修正神经网络的连接权值。随着样本训练的不断进行,最终误差逐渐减小。3层的BP神经网络已经具有优秀的对连续映射的逼近能力,完全可以满足耕地自然质量评价的计算要求。
1.1网络结构的确定
利用BP神经网络可以建立1个包括输入层、隐含层、输出层的典型3层BP神经网络模型,其中输入层就是耕地自然质量评价的指标体系,输入节点数即为耕地质量评价指标个数。输出层即最后的耕地自然质量分,节点数为1;隐含层节点个数通过经验法来决定,与评价结果的误差精度大小和隐含层神经元的多少有直接关系[14]。增加隐含层的节点数可以降低训练误差,提高训练速度,其训练效果相比于增加隐含层数更加便于观察和调整。
1.2主要参数的选取
1.2.1激活函数激活函数又被称为传递函数,是组成BP神经网络的重要部分,在1个BP神经网络中,传递函数一定是连续可微的函数,对于3层的BP神经网络模型,隐含层通常采用Sigmoid函数,而输出层的激活函数一般会选择线性函数。
1.2.2学习速率在BP神经网络模型中,学习速率将会对样本数据每次循环训练中的权值变化产生直接的影响,学习速率直接决定着BP神经网络的收敛性和收敛速度,适当调整学习速率可以更好地解决收敛速度慢和容易陷入局部最小值的问题[15]。针对不同问题,学习速率的取值各不相同。在样本学习训练中误差一样的情况下,相对较小的学习速率可以加快模型的收敛速度,但同时会增加训练次数来保证整个神经网络的稳定,使得最终的神经网络误差达到最小值。本研究通过适度减小学习速率来保证网络的收敛到最优解。
1.2.3目标误差目标误差值是网络训练过程中用来终止训练的指标。鉴于均方误差能够有效克服标准BP算法与累计误差BP算法的缺陷,本研究选用均方误差算法进行计算。均方误差MSE定义如下:
MSE=11mp∑p1p=1∑m1k-1(y^pk-ypk)2。(1)
式中:p为训練样本数量,m为输出节点个数,ypk为BP神经网络实际输出值,y^pk为BP神经网络期望输出值。
2基于遗传算法优化BP神经网络
2.1遗传算法
遗传算法是一种新兴的以优胜劣汰、自然选择和基因遗传思想为基础的优化算法。遗传算法将问题的求解表示成染色体即用编码表示的字符串,算法从一群染色体串出发将其置于问题的环境中,根据适者生存的原则,从中选取适应环境的染色体进行复制,通过交叉、变异2种基因操作产生出新一代更适合环境的染色体种群,随着算法运行,优良的品质逐渐保留并加以组合从而不断产生更加优良的个体[16]。对于遗传算法就是不断接近最优解。遗传算法是通过对参数空间编码并用随机选择作为工具,来引导搜索过程向着更高效的方向发展。遗传算法是一种启发式搜索,其搜索效率优于其他方法。为了解决神经网络容易陷入局部最小值的问题,优化初始权重是有效的解决办法。通过遗传算法对整个权值空间的全局最优搜索,寻找到接近全局最小值的权值,再使用这一组优化的权值作为BP神经网络的初始权值进行网络训练,可以精确快速地得到全局最小值。然后利用适应度函数计算子代种群中每个个体的适应度,判断是否达到适应度的目标值[17]。如果没有达到目标,就继续进入下一次迭代;如果达到目标,就停止迭代,输出当前种群中适应度最高的个体作为最优解。将最优解解码,生成BP神经网络可用的网络权值矩阵,导入到BP神经网络的结构中进行BP神经网络的运算,运算方式与独立的BP神经网络模型相同。
2.2BP神经网络的优化流程
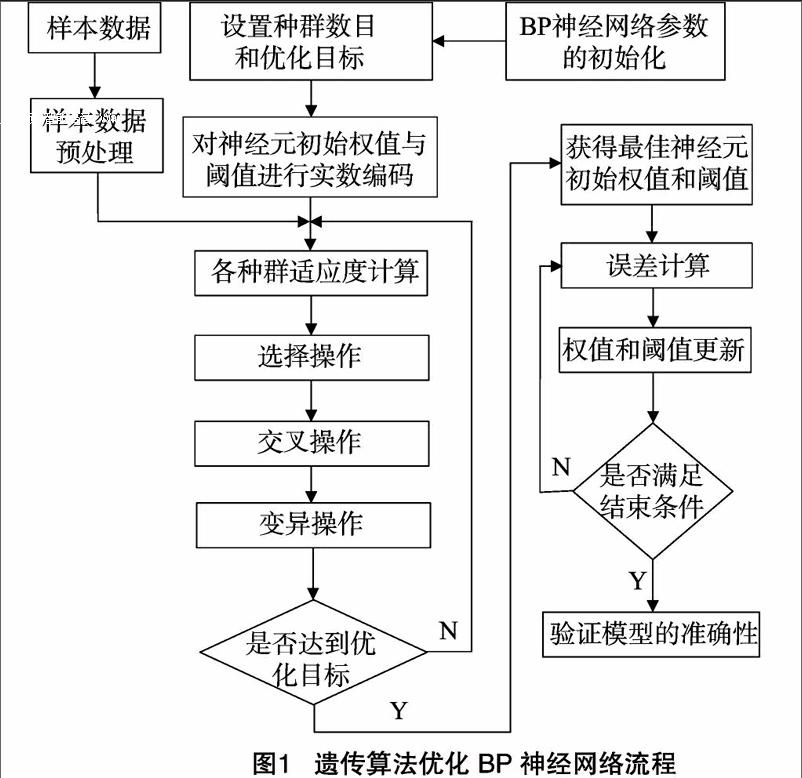
遗传算法具有较高的全局搜索能力,BP神经网络具有较强的自学能力,遗传算法和BP神经网络的结合可以充分凸显二者的优点。利用遗传算法优化初始权值,而后使用BP神网络进行网络训练达到最终结果(图1)。
2.3主要参数的选取
2.3.1选择操作选择操作是从父本中选择适应度高的个体直接遗传到下一代。这样适应度高的个体通过选择操作遗传到下一代,从而能够更加接近最优种群即最优解。目前,遗传算法中最常用的选择操作是轮盘赌选择法,即适应度比例法。适应度比例法要求每个个体的选择概率与其适应度数值成正比,适应度越大,被选择的概率就越高[18]。但是并不是适应度高的一定会被选中,这样就可能造成高适应度的基因丢失,或者最优解丢失,解决的方法是将适应度最高的个体无条件直接遗传到下一代。
2.3.2交叉概率交叉操作是将父代的2个样本部分结构进行重组而生成新的个体。较大的交叉概率Pc可以增强遗传算法开辟出新的搜索能力,但又会将已经存在高适应度的染色体破坏掉;如果交叉概率取值过低,遗传算法的进化能力就弱,无法在父代中得到适应度更高的子代个体,遗传操作陷入迟钝状态[19]。一般取值为0.25~1.0,在本次试验中,交叉概率Pc取值为0.3。
2.3.3变异概率变异操作在遗传算法中起辅助性的搜索功能,它是为了维持多样性的样本群体的保证[20]。变异操作就是取反部分基因位置上的基因值。通常采用的方法是随机选择基因值,以变异概率Pm对这些基因值进行变异。本研究遗传算法的编码采用非均匀变异,非均匀变异是随机扰动原有的基因值,得到通过变异操作后的新基因值。变异概率Pm的取值为0.1。
2.3.4终止代数终止代数T是表示遗传算法运行结束的1个参数,它表示遗传算法运行到指定的进化代数之后就停止,并将当前群体中的最佳个体作为所求问题的最优解输出。本次试验中终止代数为200。
2.3.5目标误差目标误差即目标函数值,通常是选择均方误差对神经网络在所有训练样本上所产生的误差进行计算。本研究使用BP神经网络的均方误差作为遗传算法的适应度函数,均方误差越小,其适应度越好。适应度函数计算如下:
E(XP)=11n∑n1p=1∑c1k=1[Yk,p(XP)-tk,p]2。(2)
式中:n代表训练样本数量;c代表输出端的个数;tk,p、Yk,p(Xp)分别表示训练样本p在k输出端的给定输出和实测值。
本研究针对目标误差的取值进行了预试验,分别设定了不同目标误差对本次试验数据进行处理,由表1可知,当误差为0.000 01时,优化效果较为明显,故本试验选用的目标误差为0.000 01。
2.4模型评价
泛化能力(generalization ability)是指计算机学习算法对新样本的适应能力。训练的目的是学到隐含在数据背后的规律,对具有同一规律的数据集以外的数据,随着网络不断地训练,也能仿真出合适的输出值,并非训练的次数越多越能得到正确的输入输出映射关系[21]。神经网络的性能主要用其泛化能力来衡量。针对神经网络的泛化能力,为了进一步对系统的性能进行确定,反映神经网络模型结果拟合的程度,本研究参照已有的研究经验引入“确定系数”这一概念,用以衡量模型仿真所得值与实际输出值之间的相似程度,即神经网络模型确定性程度。确定系数的计算公式如下:
r2=1-∑N1t=1(yt-y^t)21∑N1t=1(yt-yt)2。(3)
式中:N为输出值的数量,yt为实际输出值,y^t为网络仿真预测值,yt为实际输出值的均值。当模型仿真所得的值与实际输出值越相近时,所得确定性系数的值也就越逼近1,说明模型逼近效果越好,确定性能也越好。
3实例应用
3.1研究区概况
明水县位于黑龙江省西南部,地处松嫩平原西北部,东隔通肯河与海伦县相望,南与青冈相毗连,西与林甸相连,北与拜泉西北与依安相接。地势平坦,地表径流不发达,明水县东部是小兴安岭余脉的丘陵地带,西部属松嫩平原,平坦开阔,地势中部高,东西两侧渐低。明水县处于高纬度地带,是北温带大陆性季风气候,气温季节性变化明显,受大气环流和气象因素的影响,明水县年降水量变化很大,各个月份的降水分布也不平均。明水县境内有1条斜贯中部松嫩流域的分水岭,东部属松花江流域,西部和县城属嫩江流域,县内水文地质情况复杂,由西向东地下水埋藏越来越深,地下水流方向自东北向西南。明水县土壤共分为7个土类,17个亚类,20个土属,31个土种。明水县土壤基础肥力较好。明水县自然资源比较丰富,西部天然草原生产草类和中草药,东部地区盛产靰鞡草及小叶樟,水库与通肯河出产各种鱼类,地下埋藏着10余种矿物。
3.2样本的选取
本研究2015年在黑龙江省明水县各个乡镇的耕地采集140个采样点。在选取样地时,对于自然质量分相差较大的村落,相应增加选取样地数量;对于自然质量分相差较小的村落,适当减少选取样地数量。所取土样经过分析可以得到其全氮、速效钾、速效磷、土壤有机质含量、土壤酸碱度(pH值)、土壤质地、黑土层厚度、距障碍层深度这9个指标因子的相应数值,由于明水县面积较小,降水和积温在整个县域内变化较小,所以在明水县耕地质量评价中没有考虑。经过筛选,选取明水县耕地采样点样本总数140个,其中含100个训练集样本和40个测试集样本。
3.3试验结果
明水县耕地质量分等共选取了包括黑土层厚度、表层质地、距障碍层深度、土壤酸碱度(pH值)、全氮、速效磷、速效钾及土壤有机质含量在内的9个影响因子输入层,输入层拥有9个神经元,分别与9个指标因子相对应。隐含层为1层,采用经验法确定隐含层节点数为20个。输出层用1个神经元代表各评价单元所在地块相对应的耕地自然质量分,使用[0,1]区间内的实数表示。遗传算法中编码长度S=R×S1+S1×S2+S1+S2。BP神经网络中,隐含层的传递函数为 Sigmoid 函数,输出层传递函数为线性函数purelin,训练函数为trainlm,学习速率lr=0.01,最大迭代次数epoch=10 000。遗传算法的参数选取如下:种群规模popu=100,遗传代数 gen=200,交叉概率Pc=0.3,变异概率Pm=0.1。
分别基于BP神经网络模型与GA-BP网络模型对明水县140个采样点中耕地自然质量分进行5次试验(表2)。
由表2可知,BP神经网络模型的平均训练次数为321次,比GA-BP神经网络模型的平均训练次数多205次;BP神经网络模型计算结果中最大均方误差和最小均方误差的差值为0.146 8,而GA-BP网络模型计算结果中最大均方误差和最小均方误差的差值为0.070 3。通过2种模型5次试验结果分析对比可知:(1)可行性方面,2种模型的计算结果均与常规方法相差甚微,证明神经网络模型应用于耕地分等中的自然质量分计算具有可行性。(2)收敛速度方面,GA-BP网络模型的5次计算结果在训练次数上都明显小于BP神经网络模型,说明遗传算法在全局搜索能力上要有效得多,在一定程度上避免了标准BP神经网络模型陷入局部极小值,同时其收敛速度也优于BP神经网络模型。(3)稳定性方面,比较BP神经网络和GA-BP网络模型计算结果中最大均方误差和最小均方误差的差值,发现GA-BP网络模型比BP神经网络模型更稳定。(4)适应度方面,在5次计算中GA-BP网络模型的均方误差均小于BP神经网络模型的均方误差,说明GA-BP网络模型应用于耕地自然质量计算的适应度要优于BP神经网络模型。
3.4精度评价
由公式(3)可知,当确定系数越接近1时,网络仿真计算产生的实际输出值与真实值越接近,表示整个系统的精度越高,适应性越好。由表3可知,在5次试验中,遗传算法优化的BP神经网络模型(GA-BP)的确定系数最大值为0.830 3,最小值为0697 6,平均值为0.780 2,BP神经网络的确定系数最大值0.763 2,最小值为 0.583 6,平均值为 0.696 4,遗传算法优化的BP神经网络模型(GA-BP)的确定系数明显比BP神经网络的确定系数大0.083 8,同时更接近于1,说明经过遗传算法优化后的BP神经网络模型的泛化能力得到增强。在明水县耕地自然质量分的计算中,遗传算法优化的神经网络模型比BP神经网络模型精度更高。
4结论与讨论
标准BP神经网络模型能够快速拟合耕地影响因子与耕地质量分之间的非线性关系,但在训练过程中存在收敛速度过慢和容易陷入收敛局部极小值等问题。本研究提出了利用遗传算法(GA)来对于标准BP神经网络的前期振荡训练过程进行优化,并快速确定BP神经网络最优的初始权值,解决了BP神经网络模型收敛慢和容易陷入局部极小值的问题,降低了迭代次数,加快了收敛速度。试验证明,GA-BP网络模型不仅收敛速度更高,GA-BP模型的穩定性和适应度比BP神经网络模型高;且优化后的BP神经网络模型鲁棒性得到增强,精准度大幅度提高,能够更加准确地反映出耕地自然质量分与9个不同指标因子之间的关系。因此,GA-BP网络模型很大程度上使自然质量分的计算工作得到简化,并使分等结果更加科学、合理。
遗传算法具有强大优化能力,但该算法在寻找最优解过程中有可能出现“早熟现象”[22],现有的改进方法有参数改进、拓扑结构改进、混合策略等,后期研究中可考虑使用改进的遗传算法优化BP神经网络。
参考文献:
[1]李洪兴,石水莲. 辽宁省耕地利用现状及其保护策略[J]. 国土资源,2010(6):34-36.
[2]张蚌蚌,孔祥斌,郧文聚,等. 我国耕地质量与监控研究综述[J]. 中国农业大学学报,2015,20(2):216-222.
[3]付国珍,摆万奇. 耕地质量评价研究进展及发展趋势[J]. 资源科学,2015,37(2):226-236.
[4]奉婷,张凤荣,李灿,等. 基于耕地质量综合评价的县域基本农田空间布局[J]. 农业工程学报,2014(1):200-210.
[5]钱凤魁,王秋兵,边振兴,等. 凌源市耕地质量评价与立地条件分析[J]. 农业工程学报,2011,27(11):325-329.
[6]唐南奇,谭明军. 基于人工神经网络农用地分等研究Ⅰ.分等模型与精度检测[J]. 福建农林大学学报(自然科学版),2004,33(2):241-244.
[7]孔维娜,李跃进,李双异,等. 人工神经网络产量定量评价模型在县域耕地地力评价中的应用[J]. 国土与自然资源研究,2012(2):30-32.
[8]员学锋,吴普特,汪有科. BP神经网络在耕地减少预测中的应用研究[J]. 中国农业资源与区划,2005,26(4):39-41.
[9]遲宝明,林岚,丁元芳. 基于遗传算法的BP神经网络模型在地下水动态预测中的应用研究[J]. 工程勘察,2008(9):36-41.
[10]张保祥,刘青勇,卢朝霞,等. 基于神经网络和遗传算法的济南市区岩溶地下水预报模型研究[J]. 山东农业大学学报(自然科学版),2004,35(3):436-441.
[11]张学喜. 遗传算法和人工神经网络在边坡稳定性评价中的应用[D]. 合肥:合肥工业大学,2007.
[12]伍振军,刘吉平. 基于遥感和遗传BP算法的流域土地覆盖/利用分类方法[J]. 湖北地矿,2002,16(2):31,34-37.
[13]李小刚,马友华,张益,等. 基于模糊评价与BP神经网络模型的耕地质量评价对比研究——以淮北平原凤台县为例[J]. 土壤通报,2015(4):816-822.
[14]孔维娜,李跃进,李双异,等. 人工神经网络产量定量评价模型在县域耕地地力评价中的应用[J]. 国土与自然资源研究,2012(2):30-32.
[15]闻新. MATLAB神经网络仿真与应用[M]. 北京:科学出版社,2003.
[16]张豪,罗亦泳,张立亭,等. 基于遗传算法最小二乘支持向量机的耕地变化预测[J]. 农业工程学报,2009,25(7):226-231.
[17]宋戈,王越,雷国平,等. 松嫩高平原黑土区耕地资源安全的驱动机制分析[J]. 农业工程学报,2013,29(21):241-248.
[18]高娟,王海军,张怡然,等. 基于遗传算法和支持向量机的城镇土地定级方法研究[J]. 华中师范大学学报(自然科学版),2014,48(6):917-922,929.
[19]骆成凤,刘正军,王长耀,等. 基于遗传算法优化的BP神经网络遥感数据土地覆盖分类[J]. 农业工程学报,2006,22(12):133-137,后插1.
[20]宋戈,邹朝晖,王越. 东北粮食主产区县域耕地产能核算及其影响因子分析[J]. 农业工程学报,2014,30(24):308-317.
[21]雷英杰. MATLAB遗传算法工具箱及应用[M]. 西安:西安电子科技大学出版社,2005.
[22]周洪伟,原锦辉,张来顺. 遗传算法“早熟”现象的改进策略[J]. 计算机工程,2007,33(19):201-203.

