初中数学解题中数形结合思维的引入实践微探

叶玉娣

（浙江省杭州市桐庐县旧县中心学校，浙江杭州 311500）

数学作为一门逻辑性要求较强的科目，对初中生而言是一项学习挑战。数学课程作为数与形的结合，只有把握好数与形间的本质，才能准确解答出问题。数形结合思想作为初中生必须要具备一种解题思想，将其应用至解题活动中，有助于学生更好把握数学知识，依据知识间联系构建知识体系，从整体上提升解题能力。

1 在数与式中的应用

为了使学生能够理解数形结合思想的本质，教师需要在课堂教学中以问题解析的方式，为学生重点讲解此方法的应用技巧。如，教师在教学有关正负数的知识时，事先画出数轴，并邀请学生介绍数轴中对应数字的具体含义，旨在加深学生对于数轴中各项数值的认知。在学生掌握一定基础后，为学生设计如下问题，鼓励学生自主解答。

已知数 a、b、c在数轴上的位置如图所示，化简|a+b|-|c-b|的结果是 ______．

解析：先从数轴上a、b、c的位置关系可知：c＜a＜ 0；b＞ 0且 |b|＞ |a|，接着可得 a+b＞ 0，c-b＜ 0，然后即可化简|a+b|-|c-b|可得结果。

解：由数轴上点的位置可得：c＜ a＜ 0＜ b，且|a|＜ |b|，∴ a+b＞ 0，c-b＜ 0，则 |a+b|-|c-b|=a+b+cb=a+c.故答案为：a+c

2 在变化规律中的应用

规律型问题的解题方法大多是借助观察，对比特殊变量或位置，从中截取数据特征，将获取的数据进行分组比较。但是此种解题方式过于繁琐，为了节省时间可以采取数形结合的方法，虽然图形和数字的形式不同，但它们可以表示相同的规律，从而帮助学生更好把握知识间的内在关联，从而建立知识间的数形联系，不断提高解决效率。

如：有一个四等分转盘，在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌，如图1．若将位于上下位置的两个字牌对调，同时将位于左右位置的两个字牌对调，再将转盘顺时针旋转90°，则完成一次变换．图2，图3分别表示第1次变换和第2次变换．按上述规则完成第9次变换后，“众”字位于转盘的位置是（ ）

A．上 B．下 C．左 D．右

解析：根据题意可知每一次变换后相当于逆时针旋转了 90°，经过 4次变换后会回到原始位置，所以按上述规则完成第 9次变换后，相当于第一次变化后的位置关系，分析比较可得答案．

解：根据题意可知每一次变换后相当于逆时针旋转了 90°，经过 4次变换后会回到原始位置，所以按上述规则完成第 9次变换后，“众”字位于转盘的位置是应该是第一次变换后的位置即在左边， 比较可得C符合要求。

3 在二次函数与不等式组中的应用

在解答此类问题时，依据数学题干中给出的条件，判断问题最终求的是什么。以求解不等式或不等式组解集这类问题为例，需要事先确定题干中字母的取值范围。虽然此种方式的理解难度比较大，但是若是能寻找到技巧，分析多个条件，将会获取事半功倍的效果。

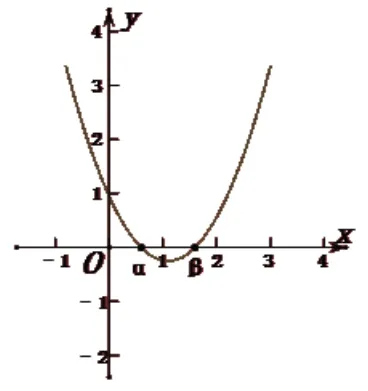
方程 7x2-（k+13）x+k2-k-2=0（k是实数）有两个实根α、β，且0＜α＜1，1＜β＜2，那么k的取值范围是（ ）

A．3＜k＜4

B. -2＜ k＜ -1

C．3＜ k＜ 4或 -2＜ k＜ -1

D．无解

分析：若用数形结合的方法，先画出抛物线 y=7x2-（k+13）x+k2-k-2的草图，

易知当 x=0时，y＞ 0 ，k2-k-2＞0，所以k＞2或＜-1；当x=1时，y＜0，k2-2k-8＜0，所以-2＜k＜4

当x=2时，y＞0,k2-3k＞0，所以k＞3或k＜0

解不等式组可得k的取值范围是3＜k＜4或-2＜k＜ -1， 故选 C．

4 在函数中的应用

函数作为初中数学教学的一大难点，也是最令学生感到棘手的知识。基于此情况，教师在解题教学中需要引导学生巧用数形结合思想，将数量关系借于图形及其性质，使其直观化，形象化，从而使问题得以解决。

二次函数 y=ax2+bx+c的图象的顶点在第三象限 ,且不经过第四象限,则此抛物线开口向_______ ，c的取值范围______ ，b的取值范围______ ，b2-4ac的取值范围______。

解：由题意画出图象，如图：

从而判断：a＞0, c≥0

∴对称轴：x=-＜0

∴b＞0

图象与x轴有两个交点：

∴ ＞ 0 即 b2-4ac＞ 0

5 在函数图形中的应用

由于学生对函数图像特征缺少深入的了解，导致在解题过程中很难准确把握解析式，两者转换非常困难，解题效果无法达到预期效果。基于此问题，教师需要引导学生深度研究其本质，在解题过程中巧用数形结合思想，培养学生的数学思维，展开针对性的训练，从而帮助学生更快理解并掌握其知识。

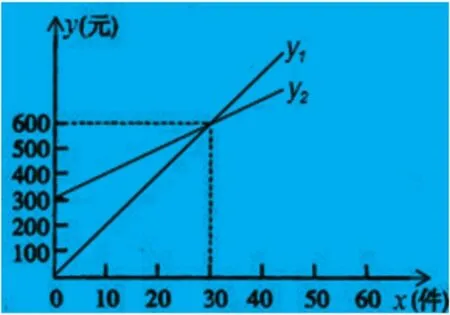
某公司推销一种产品 ,设 x(件 )是推销产品的数量 ,y(元 )是推销费 ,如图表示了公司每月付给推销员推销费的两种方案 ,看图解答下列问题 : 求y1与y2的函数解析式；解释图中表示的两种方案是如何付推销费的；如果你是推销员,应如何选择付费方案.

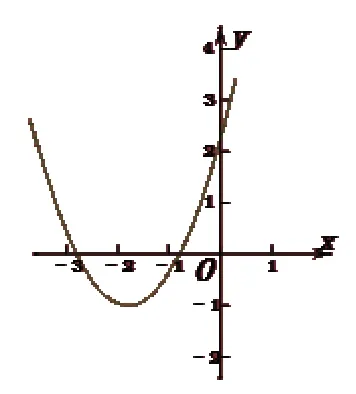
本题主要考察了用待定系数法求一次函数这一内容，在解答此题时可以采取数形结合思想，能够使解题过程变得更加简单。在解答第一问时，由图已知两点，可根据待定系数法列方程，求出函数关系式；在解答第二问时，根据两条直线的截距和斜率，可解释两种方案的推销费用；在解答第三问时，由图可看出两直线的交点为 30，当x＞30时，y1可获得较多的推销费用，当x=30时，两种方案获得的推销费用一样；当x＜30时，y2可获得较多的推销费用。

综上所述，数形结合思想的引用为提升学生学习能力带来诸多帮助，借助数与形间的转换，全面解读数学问题，培养学生数学思维，进一步提升了学习成绩。因此，教师需要提高对数形结合思想的重视，开展多种类型的解题训练活动，以此不断提升学生的解题能力。

[1] 王爱花.初中数学数形结合思想教学研究与案例分析[J].中国校外教育,2017(05)

[2] 蔡清润.数形结合教学方法在初中数学中的运用[J].西部素质教育,2017,3(01)

[3] 吴耀耀. 基于新课程标准下中学数学“数形结合”的教与学[D].宁夏师范学院,2016.