基于改进的共轭梯度算法重构地下水污染源项

邢利英,张国珍

(1.兰州交通大学环境与市政工程学院,甘肃兰州 730070;2.南阳师范学院土木与建筑工程学院,河南南阳 473061)

基于改进的共轭梯度算法重构地下水污染源项

邢利英1,2,张国珍1

(1.兰州交通大学环境与市政工程学院,甘肃兰州 730070;2.南阳师范学院土木与建筑工程学院,河南南阳 473061)

针对地下水污染源项的识别问题,为重构非恒定地下水污染源项,采用有限差分格式离散方程,同时附加终端观测值,利用改进的共轭梯度算法反演地下水的污染源项。结果表明:对于连续以及不连续不可导的污染源项均能够被重构;此外,考虑测量误差的影响,数值结果显示在有测量误差的情况下,该算法也能较好地反演污染源项,充分说明改进的共轭梯度算法反演地下水污染源项是有效的。

地下水;污染源项;重构;反问题;共轭梯度法

随着现代化的快速发展,大量工农业污染物的排放导致地下水污染严重。地下水中污染物的迁移过程作用时间长,影响范围大,在迁移过程中还涉及水文地理条件、物理反应、化学反应等诸多因素,使得污染物迁移过程变得极为复杂,并表现出非线性行为。由于地下水系统本身的隐藏性和复杂性,地下水污染并没有引起业界足够的重视。最近的一份调查报告显示,作为主要淡水资源之一的地下水已经被氮、碳氢化合物、有毒有害的微量元素严重污染,并且呈现出由点到面、由城镇向农村发展的趋势,所以此类问题变得越来越棘手[1-4]。

事实上,在地下水污染物的实际测量中,有很多信息难以准确测量,甚至无法测量,然而可以通过一些已知信息来确定未知的信息,所以在地下水的反问题研究中包含参数识别、边界确定、源项识别等几类问题,而污染源项识别问题在地下水污染中具有特殊的意义。目前已有大量的文献研究地下水污染源的识别问题,Li等[5]应用全域多元二次曲面方法反演污染源项;Hazart等[6]设计基于马尔科夫链的贝叶斯参数识别法重构点源的位置、释放时间和源强的大小;王建平等[7]基于马尔科夫链的贝叶斯方法进行了水质参数的不确定性研究;李子等[8]采用时空全域径向基函数配点法构造惩罚函数,通过搜寻形状因子和比例因子来确定污染源项的位置及强度;Zeng等[9]采用稀疏网格差值的贝叶斯方法确定污染源项。关于污染源项反演的其他方法请参考文献[10-14]。然而,之前的研究中很少采用改进的共轭梯度法反演污染源项。

共轭梯度法在数学理论分析中应用较多,Deng等[15]采用共轭梯度方法重构了传热方程的辐射项系数,数值结果表明该方法有效地反演了辐射项系数;Yang等[16]应用共轭梯度方法重构传热方程的源项。本文设计一种改进的共轭梯度方法反演地下水污染源项。

1 地下水污染控制方程

地下水污染溶质的输运和迁移过程是一个相当复杂的物理化学过程,主要包括对流、扩散、吸附、交换和其他的物理化学过程。简单起见,这里只考虑沿主流方向,结合初边界条件,污染物迁移模型可用一维非稳定对流扩散方程表示:

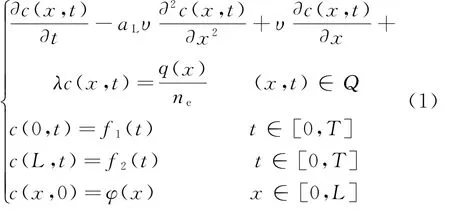
式中:c(x,t)为测点(x,t)的污染物浓度,mg/L; q(x)为污染源项,仅考虑为空间变量的函数,mg/(L·s); aL为污染物沿x方向的扩散度,m;υ为地下水实际的流速,m/s,通过水动力模型计算给出;λ为污染物的衰减系数,s-1;ne为有效地孔隙率,无量纲; Q为计算区域;T为溶质输运时间,s;L为主流方向长度,m;f1(t)和f2(t)为边界条件;φ(x)为初始条件。

简言之,如果方程组(1)中的参数aL、υ、λ、ne、q(x)以及初边界条件均已知,则方程组(1)构成一个正问题,可以通过实验和数值模拟的方法预测污染物浓度c(x,t)。然而,大多数情况下,地下水的污染源项并不能准确地获得,因此可以通过已知的参数和初边界条件推测未知的污染源项,方程组(1)则转变为一个反问题。

解决上述反问题,通常可以附加一组容易获得的终端观测值,一般应用如下的形式:

式中,cT(x)为终端观测值。

由此,式(1)和(2)就构成了一个关于源项识别的反问题,可以应用迭代的方法求解。

2 差分方程

假设计算区域为Q=[0,L]×[0,T],用有限差分法求解偏微分方程的源项识别问题,首先对计算区域Q进行网格剖分。将区域Q划分M×N等分,则空间步长和时间步长分别为测点(xj,tn)是网格节点。

式中:h,τ分别为空间步长和时间步长;M、N为两个整数。则方程组(1)中的第一个式子可转化如下简单的形式:

式中:ct、cxx、cx分别为污染物浓度c关于时间的一阶导数、空间的二阶导数、空间的一阶导数。四点隐格式的差分方程为

由于隐格式的差分方程是无条件稳定的,因此可应用任意步长求解线性方程(9)。下面将详细地介绍改进的共轭梯度算法。

3 改进的共轭梯度算法

共轭梯度算法由Fletcher等[17]首次提出的,作为一种简单有效的迭代技术,广泛应用于地理学和传热学方程的源项及扩散项系数反演。在大中型线性和非线性的无约束优化问题中,共轭梯度算法尤其有效。共轭梯度算法的基本思路为结合共轭性和最速下降法,构建一组共轭负梯度方向,沿着下降的方向寻找目标函数的最小值,合适终止条件的共轭梯度法实际上是一类迭代正则化方法。鉴于共轭梯度的特点,本文拟进一步改进共轭梯度算法重构地下水污染源项。

设非线性优化问题的控制方程可以表示为

其中D(F):X→Y为一有界线性算子,X和Y属于Hilbert空间。对于x∈X,通常设F为一连续性的算子,所以上述非线性优化问题可转化为

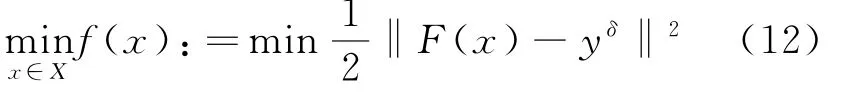
式中:f(x):Rn→R是一连续可微的函数;‖·‖2为欧几里得模数;δ为误差范围。

尤其是当n很大时,共轭梯度相当有效,式(12)则可转化为

详细的改进共轭梯度算法步骤[15,20]如下:

步骤1:设k=0,选择一个迭代初始值q0(x)= 0,x∈[0,L];

步骤2:求解初边值问题(式(1)),得到其解ck,此时q(x)=qk(x);

步骤3:确定残差rk=gδ-ck,求解下面的共轭方程,其解为uk(x,t);

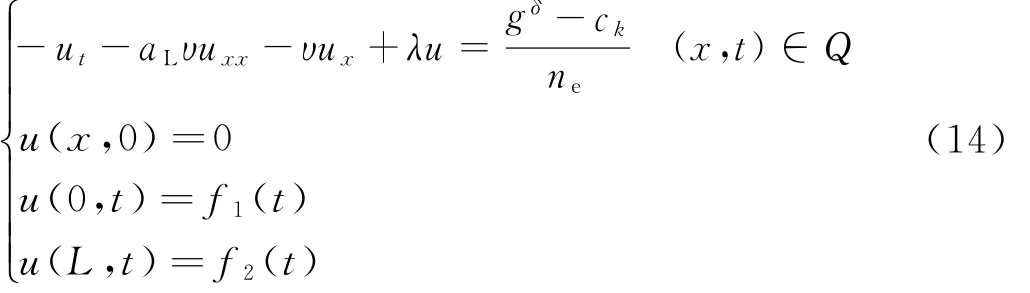
步骤4:计算sk=uk+αk-1sk-1,其中

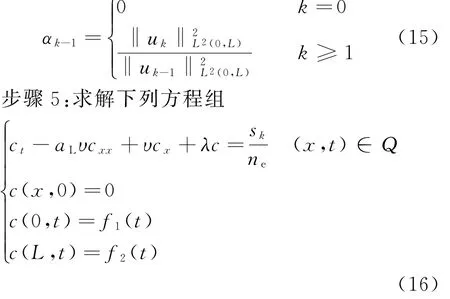
并得到其解为c:=dk(x,t),令

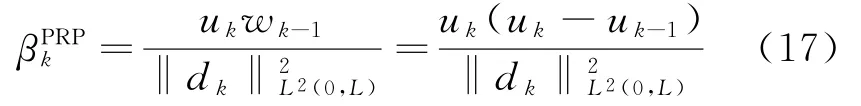
其中wk-1=uk-uk-1,则有qk+1=qk+βksk。

步骤6:增加迭代次数k,执行循环到步骤2。任取γ>1,当k∈Ν,第一次满足‖gk-g‖L2(0,L)≤γδ时终止循环。

4 算 例

本文设计了3个算例来检验上述算法的有效性。a.试验1。采用一假设的数值算例验证改进共轭梯度法的有效性,控制方程如下:

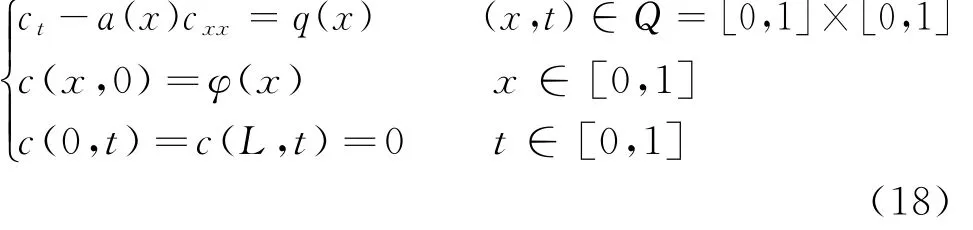
当式(18)取第一组参数:a(x)=1,φ(x)=sin (2πx),q(x)=2π2sin(2πx),时间步长和空间步长分别取1/100s和1/100 m,应用改进的共轭梯度算法反演污染源项的结果见图1(a)。从图1(a)中可以看出,当迭代次数K=50时,反演结果已经很好地与真实解吻合。

当取第二组参数:φ(x)=sin(x),q(x)=|(x -1)(x-3)|,x∈[0,4],则反演结果见图1(b)。从图1(b)中可以看出,除了2个不可导点,源项被较好地反演。以上2组试验很好地说明了共轭梯度法能有效地反演控制方程源项,可以应用到实际问题源项的重构中。

b.试验2。对淄博沣水南部地区的地下水硫酸污染源强度进行数值反演,相关数据参考文献[21]。根据计算区域的水文地质条件,取x=4 000 m,T= 11 a,并取αL=1 m,u=1 m/d,ne=0.25,空间步长h=100 m,时间步长τ=0.5 a。通过线性拟合,初边值条件表达式为

附加终端观测值为拟合后的线性函数c(x,11)=0.102 6x+152。

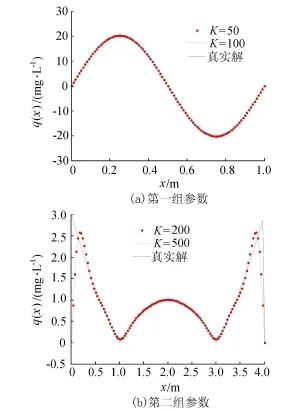
图1 试验1的反演结果

应用改进的共轭梯度算法进行反演,附加数据和反演结果的对比见图2。从图2中可以看出当迭代次数K=30时,污染源项已经较好地被重构,充分说明该方法收敛速度较快,反演结果稳定。采用cδT(x)=cδ(x,T)=c(x,T)[1+δrandom(x)]计算测量误差,当测量误差δ分别为2%和5%时,污染源项的真值和反演结果的计算误差分别为3.04%和2.83%,比参考文献[21]的误差4.18%要小。

c.试验3。为了进一步验证改进共轭梯度算法的有效性,将污染源项函数变化为一分段函数(式(20)),空间距离增至为6 000 m,其他模型参数与试验2相同。不同迭代次数K和不同测量误差δ的反演结果见图3。

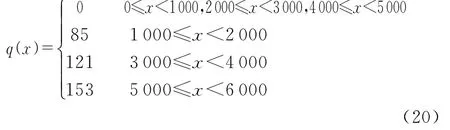
由于污染源项的不连续性,当迭代次数增大到100次时,污染源项才被较好地重构。类似地,考虑测量误差δ的影响时,尽管污染源项的不连续性,而且测量误差也会产生影响,但是模拟结果也比较正常,充分证明改进共轭梯度算法的稳定性和较大的容错性。

5 结 语

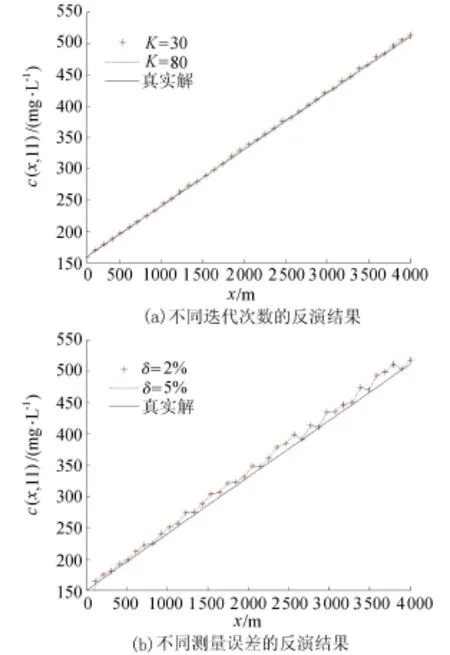
图2 实际问题的反演结果与附加数据的比较

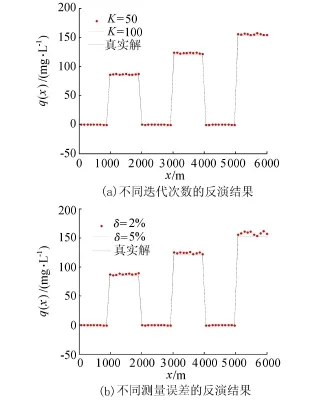
图3 试验3的反演结果

采用有限差分法离散地下水控制方程,应用改进的共轭梯度算法重构地下水污染源项。数值模拟结果表明,对于性质友好的源项以及不连续不可导的源项均能够被反演。考虑测量误差的影响,结果显示在有测量误差的情况下也能得到稳定解,充分说明改进的共轭梯度算法是一种有效的反演方法。污染源项如果是连续的函数,迭代次数大约为50次,反演结果趋于稳定;污染源项如果是不连续的函数,迭代次数大约为100次时,反演结果趋于真实解,从而说明改进的共轭梯度算法是一种快速稳定的反演方法。

[1]ZHOU H Y,GOMEZ-HEMANDEZ J J,LI L P. Inverse methods in hydrogeology:evolution and recent trends[J].Advances in Water Resources, 2014,63:22-37.

[2]孙才志,陈相涛,陈雪姣,等.地下水污染风险评价研究进展[J].水利水电科技进展,2015,35(5):152-161. (SUN Caizhi,CHEN Xiangtao,CHEN Xuejiao,et al. Recent advances in groundwater contamination risk assessment[J].Advances in Science and Technology of Water Resources,2015,35(5):152-161.(in Chinese))

[3]YEH W W G.Review:optimization methods for groundwater modeling and management[J]. Hydrogeology Journal,2015,23(6):1051-1065.

[4]朱嵩.基于贝叶斯推理的环境水力学反问题研究[D].杭州:浙江大学,2008.

[5]LI Zi,MAO Xiaokang,ZHOU Kang.Global multiquadric collocation method for groundwater contaminant source identification[J].Environmental Modelling&Software,2011,26(12):1611-1621.

[6]HAZART A,GIOVANNELLI J F,DUBOST S,et al.Inverse transport problem of estimating point-like source using a Bayesian parametric method with MCMC[J].Signal Processing,2014,96:346-361.

[7]王建平,程声通,贾海峰.基于MCMC法的水质模型参数不确定性研究[J].环境科学,2006,27(1):24-30. (WANG Jianping,CHENG Shengtong,JIA Haifeng. Markov chain monte carlo scheme for parameter uncertainty analysis in water quality model[J]. Environmental Science,2006,27(1):24-30.(in Chinese)).

[8]李子,毛献忠,周康.污染物非恒定输运逆过程反演模型研究[J].水力发电学报,2013,32(6):115-121. (LI Zi,MAO Xianzhong,ZHOU Kang.Inversion model for the inverse process of unsteady pollutant transport[J].Journal of Hydroelectric Engineering, 2013,32(6):115-121.(in Chinese))

[9]ZENG Lingzao,SHI Liangsheng,ZHANG Dongxiao, et al.A sparse grid based Bayesian method for contaminant source identification[J].Advances in Water Resources,2012,37:1-9.

[10]WILLIAMS B,CHRISTENSEN W F,REESE C S. Pollution source direction identification:embedding dispersion models to solve an inverse problem[J]. Environmetrics,2011,22(8):962-974.

[11]WANG Hui,JIN Xin.Characterization of groundwater contaminant source using Bayesian method[J]. Stochastic Environmental Research and Risk Assessment,2012,27(4):867-876.

[12]OU Yang,WANG Xiaoyan.Identification of critical source areas for non-point source pollution in Miyun Reservoir watershed near Beijing,China[J].Water Science&Technology,2008,58(11):2235-2241.

[13]刘蕴,方晟,李红,等.基于四维变分资料同化的核事故源项反演[J].清华大学学报(自然科学版),2015,55 (1):98-104.(LIU Yun,FANG Sheng,LI Hong,et al.Source inversion in nuclear accidents based on 4D variational data assimilation[J].Journal of Tsinghua University(Science and Technology),2015,55(1): 98-104.(in Chinese))

[14]轩晓博,逄勇,李一平,等.金属矿区重金属迁移对水体影响的数值模拟[J].水资源保护,2015,31(2):30-35.(XUAN Xiaobo,PANG Yong,LI Yiping,et al. Numerical simulation of influence of heavy metal migration on water in metallic mining areas[J]. Water Resources Protection,2015,31(2):30-35.(in Chinese))

[15]DENG Zuicha,QIAN Kun,RAO Xiaobo,et.al.An inverse problem of identifying the source coefficient in a degenerate heat equation[J].Inverse Problems in Science and Engineering,2014,23(3):498-517.

[16]YANG Liu,DENG Zuicha,YU Jianning,et al. Optimization method for the inverse problem of reconstructing the source term in a parabolic equation [J].Mathematics and Computers in Simulation, 2009,80(2):314-326.

[17]FLETCHER R,REEVES C M.Function minimization by conjugate gradients[J].The Computer Journal, 1964,7(2):149-154.

[18]肖庭延,于慎根,王彦飞.反问题的数值解法[M].北京:科学出版社,2003:115-120.

[19]姚胜伟.几类共轭梯度算法的研究[D].上海:华东理工大学,2014.

[20]YAO Shengwei,LU Xiwen,NING Liangshuo,et al. A class of one parameter conjugate gradient methods [J].Applied Mathematics and Computation,2015, 265:708-722.

[21]范小平,李功胜.确定地下水污染强度的一种改进的遗传算法[J].计算物理,2007,24(2):187-191.(FAN Xiaoping,LI Gongsheng.An improved genetic algorithm for groundwater pollution[J].Chinese Journal of Computational Physics,2007,24(2):187-191.(in Chinese))

Reconstruction of groundwater pollution source term with improved conjugate gradient algorithm

XING Liying1,2,ZHANG Guozhen1
(1.School of Environmental and Municipal Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China; 2.School of Civil and Architecture Engineering,Nanyang Normal University,Nanyang 473061,China)

In order to reconstruct the unsteady pollution source term of groundwater for its identification, the finite difference scheme was used to discretize the equations,terminal observed data were appended, and an improved conjugate gradient algorithm was used to reconstruct the pollution source term.The results show that,whether the pollution source term is a continuous function or a discontinuous and nondifferentiable function,it can be reconstructed.In addition,with consideration of measurement errors,the proposed method can reconstruct the source term effectively,indicating that the improved conjugate gradient algorithm is effective in reconstructing the groundwater pollution source term.

groundwater;pollution source term;reconstruction;inverse problem;conjugate gradient algorithm

X523

A

1004-6933(2017)03- 0042- 05

2016 06-08 编辑:王 芳)

10.3880/ji.ssn.1004-6933.2017.03.009

国家自然科学基金(51468033)

邢利英(1980—),女,讲师,博士研究生,主要从事环境水力学方面研究。E-mail:lyxing2011@163.com