实验室尺度下气水两相裂缝型介质弹性波速度的数值模拟分析
段 茜,刘向君
(1.西南石油大学地球科学与技术学院,四川成都610500;2.西南石油大学理学院,四川成都610500)
实验室尺度下气水两相裂缝型介质弹性波速度的数值模拟分析
段 茜1,2,刘向君1
(1.西南石油大学地球科学与技术学院,四川成都610500;2.西南石油大学理学院,四川成都610500)
岩心的非均质结构使得采用实验手段研究弹性波速度与岩石力学参数之间的关系时面临较大困难,且超声波测试工作量大,耗资耗时。基于弹性波动理论和Wood孔隙流体模量模型,采用交错网格有限差分方法对气水两相裂缝型介质的弹性波场进行了数值模拟。计算了岩样在不同裂缝分布位置、孔隙度、裂缝产状、裂缝密度和含水饱和度情况下的纵、横波速度及波速比,讨论了这些因素对波速的影响。模拟分析结果表明,该数值模拟计算方法简单、精度高,对利用岩石波速来反演岩石的孔隙结构有一定的指导作用。
弹性波速度;波动理论;气水两相;介质;裂缝
基于岩石中波的传播性质的地震勘探方法是目前地球物理勘探中最主要的方法之一。岩石的整体性质可以通过对弹性波速度的分析来获得,如果知道岩石的整体性质与孔隙及孔隙流体之间的关系,就可以利用地层的速度分析去预测地下流体是否存在。纵波和横波关于岩石的孔隙度和饱和度的变化有不同的响应规律,岩石物理研究主要是通过岩石的纵波速度分析得到岩性参数[1-3],但是单纯利用纵波速度来反演地层孔隙结构有很大困难,目前对横波速度的测量和分析引起了研究者极大的关注。利用纵、横波,尤其是波速比资料,已成为探明地下岩石物性的有力工具。关于横波速度的预测[4-5]和实验测量工作[6-12]已开展很多,但都存在一些问题。预测横波速度时大都将岩石考虑为均匀介质,通过岩石物理模型来估算,事实上,岩石是非均质结构的。横波速度的实验测量精度非常低,远远低于纵波速度的测量精度,原因是对横波速度进行测量时会受岩石的非均质结构,测试方法以及纵波、横波换能器特性等众多因素的影响,且其测试结果缺少精度评价。已有的通过纵波间接测试得到横波速度的方法[13-14]有待进一步验证。本文从弹性波动理论出发,结合等效介质理论,采用交错网格有限差分方法[15]对实验室尺度下气水两相裂缝型介质的弹性波场进行了数值模拟,讨论了不同裂缝分布位置、孔隙度、裂缝产状、裂缝密度和含水饱和度对岩样纵、横波速度及波速比的影响。
1 岩样纵、横波速度的计算
岩样的纵、横波速度可以根据弹性波透过岩样时的传播时间和岩样长度来计算。本文对超声波透射实验进行数值模拟,以发射探头的激发信号为震源,模拟其通过不同气水两相裂缝型岩样后接收探头的波形,再拾取接受端波形的初至来得到波的传播时间,利用公式(1)和公式(2)即可计算出纵波速度vP和横波速度vS,还可进一步得到波速比vP/vS以及各种动弹性参数。

式中:L为岩样长度;TP为纵波传播时间;TS为横波传播时间。
2 一阶应力 速度弹性波动方程
二维非均匀各向同性介质中的弹性波,其一阶应力 速度方程组[16]为:
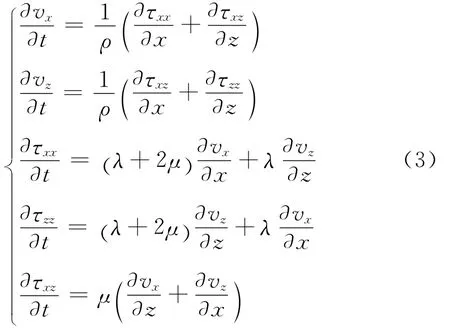
式中:vx和vz分别是质点振动速度的水平分量和垂直分量;τxx,τzz,τxz是应力张量;ρ是密度;λ和μ是拉梅系数。
2.1 震源
震源子波函数可以用最小相位子波或零相位(雷克)子波等表示,采用最小相位子波时,其数学表达式为:
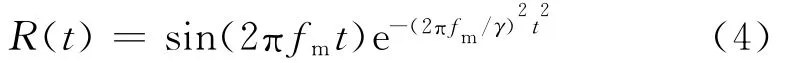
式中:t为子波长度;fm表示子波的主频;γ为控制波形形状的常数,γ越大,子波能量越向后延迟。本文采用的震源子波主频为100kHz,震源持续时间为4μs,γ取4.0,波形如图1所示。
图1 震源子波
2.2 稳定性条件
采用二阶时间精度和八阶空间精度对弹性波场进行模拟,根据董良国等[17]提出的一阶弹性波方程交错网格高阶差分稳定性分析条件,可以得到稳定性条件为:
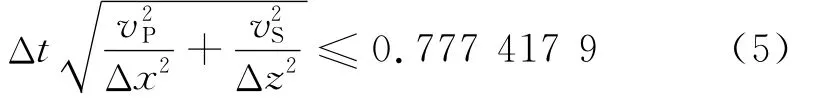
2.3 边界条件
本文将完全匹配层(PML)吸收边界条件[18-19]应用于人工截断边界处,具体做法是在研究区域边界的周围加上完全匹配层吸收介质,波从研究区域经过边界进入完全匹配层时不会产生任何反射。而在吸收层内,随着传播距离的增加,波呈指数规律衰减,从而达到吸收边界的效果。该吸收边界条件是求解弹性波动力学方程组时最有效的吸收边界条件。
3 Wood孔隙流体模量模型
由Wood孔隙流体模量模型[20]可以给出流体悬浮物或流体混合物的声波速度:

式中:KR为混合物的有效体积模量;ρ为混合物的密度。
在要求取烃类和水混合的情况下,孔隙流体体积模量KR为:
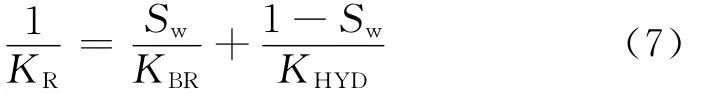
式中:Sw为含水饱和度;KBR和KHYD分别为盐水和烃类的体积模量。而孔隙流体的密度ρ为:
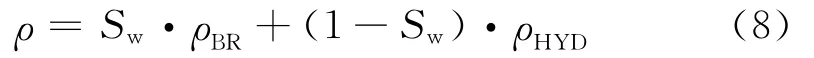
式中:ρBR和ρHYD分别为盐水和烃类的密度。
在流体替换过程中,Wood孔隙流体模量模型常用于估算孔隙流体的体积模量和密度。
4 弹性波速度计算精度评价
设计一无裂缝的均匀岩样,其尺寸为50mm(长度)×50mm(直径),密度为2 700kg/m3,设岩样的纵波速度为6 200m/s,横波速度为3 800m/s,采样时间步长为10ns。将岩样的纵向剖面区域划分成250×250的网格,因此空间网格的步长为0.2mm。在质点振动速度的水平分量vx上布置震源,震源位于点(25mm,0)处,接收探头位于点(25mm,50mm)处。质点振动速度水平分量vx在6μs时的波场快照如图2所示,接收端波形如图3所示。从接收端得到的vx波形图上提取首波初至时刻即为纵波的传播时间,为8.07μs。已知岩样长度为50mm,由公式(1)计算得到纵波速度为6 196m/s,与设定纵波速度(6 200m/s)相比,误差非常小,仅为0.06%。由于考虑的是质点振动速度的水平分量vx,因此在接收端横波的振幅有极大值,为减小拾取横波初至时刻的误差,计算横波传播时间采用峰值传播时间。震源的峰值位于0.23μs处,横波的峰值位于13.26μs处,由此得到横波的传播时间为13.03μs,由公式(2)计算得到横波速度为3 837m/s,与设定横波速度(3 800m/s)相比,误差也较小,为0.97%,远远高于实验测量精度,完全满足分析讨论需求。
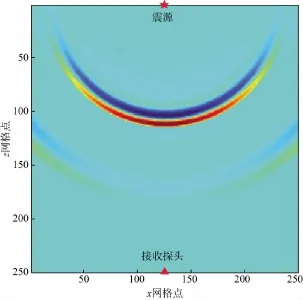
图2 水平分量波场快照
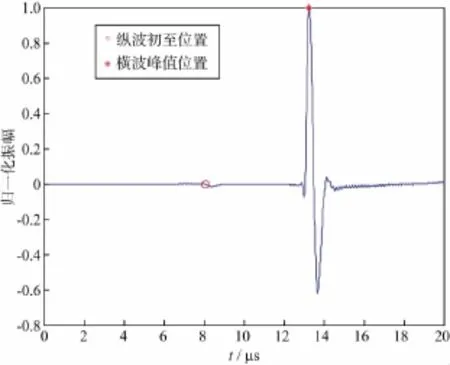
图3 接收端vx波形
5 模拟结果分析
5.1 单裂缝分布对弹性波速度的影响
对于单裂缝,其几何形态由中心坐标及倾角确定,下面将分别讨论这些因素对弹性波速度的影响。
5.1.1 裂缝中心横坐标对弹性波速度的影响
设计一单裂缝气水两相孔隙流体模型,气和水的密度分别为0.72kg/m3和1 000kg/m3,体积模量分别为0.1GPa和2.1GPa,设孔隙的含水饱和度为50%,按照Wood孔隙流体模量模型即可计算得到孔隙流体的密度ρ为500.36kg/m3,体积模量KR为0.19GPa,从而得到裂缝孔隙流体中的纵波速度为616.22m/s,横波速度为0。设缝长为8mm,缝宽为3mm,裂缝与水平线之间的倾角为0,裂缝中心纵坐标为25mm,中心横坐标分别为5,10,15,20,25,30,35,40,45mm。其中,中心横坐标为5,15,25mm时质点振动速度水平分量vx在7μs时的波场快照如图4所示。纵、横波速度及波速比随裂缝中心横坐标的变化曲线如图5所示。从模拟结果可以看出,只有在裂缝中心横坐标靠近岩样模型中心位置,即裂缝即将或已经穿过震源与接收探头间的连线时,弹性波速度才会发生变化。裂缝中心横坐标越靠近模型中心,纵、横波速度越小,波速比越大。如果裂缝处于岩样模型边缘位置,即裂缝远离震源与接收探头间的连线时,模拟得到的岩样弹性波速度与无裂缝时的结果一样,弹性波速度未发生变化。原因是当裂缝在震源与接收探头间的连线上时,阻碍了弹性波的传播路径,弹性波发生绕射和转换,传播路径变长,使得接收端纵、横波的初至时间均延后。裂缝的分布位置对模拟结果的影响极大,因此,后面的模拟将重点考虑裂缝位于震源与接收探头间的连线上时,弹性波速度发生变化的情形。
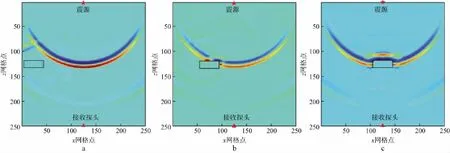
图4 裂缝中心横坐标分别为5mm(a),15mm(b)和25mm(c)时的水平分量波场快照
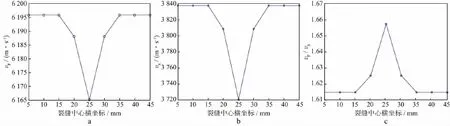
图5 纵波速度(a)、横波速度(b)和波速比(c)随裂缝中心横坐标变化曲线
5.1.2 裂缝中心纵坐标对弹性波速度的影响
设裂缝孔隙流体的含水饱和度为50%,缝长为8mm,缝宽为3mm,裂缝与水平线之间的倾角为0,裂缝中心横坐标处于模型中心,即为25mm,中心纵坐标分别为10,15,20,25,30,35,40mm。其中,中心纵坐标为10,25,40mm时质点振动速度水平分量vx在7μs时的波场快照如图6所示。纵、横波速度及波速比随裂缝中心纵坐标的变化曲线如图7所示。从模拟结果可以看出,当裂缝中心纵坐标越靠近岩样模型中心位置时,纵、横波速度越大,波速比越小,越靠近震源或接收探头时,纵、横波速度越小,波速比越大。由简单的几何学知识知道,底边确定的面积一定的三角形,当它是等腰三角形时周长最小,因此,当裂缝中心纵坐标位于岩样模型中心时,纵、横波的传播路径最短,纵、横波速度最大。
5.1.3 缝长对弹性波速度的影响
设裂缝位于岩心模型中心,中心横坐标为25mm,中心纵坐标为25mm,裂缝孔隙流体的含水饱和度为50%,裂缝与水平线之间的倾角为0,缝宽为3mm,缝长分别设置为6,10,14,18,22mm,其中,缝长为6,14,22mm时质点振动速度水平分量vx在7μs时的波场快照如图8所示。随着缝长的增加,阻碍传播路径的反射界面范围越来越大,纵、横波的传播路径变长,使得接收端纵、横波的初至时间均延后。
最后,选择这个题材,就是希望引发各界对非物质文化保护的思考和关注。是否表面看似优良的物质条件就能够带给民众幸福感?农耕文明和城镇化之间又该如何过度?远离文化沃土的少数民族该如何去竭力保护自己的民族文化?
纵、横波速度及波速比随缝长变化的曲线如图9所示,当裂缝位于岩心模型中心时,随着缝长的增加,纵波速度减小,横波速度减小,波速比增高。
5.1.4 缝宽对弹性波速度的影响
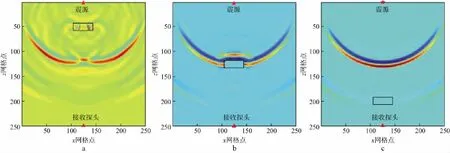
图6 裂缝中心纵坐标分别为10mm(a),25mm(b)和40mm(c)时的水平分量波场快照
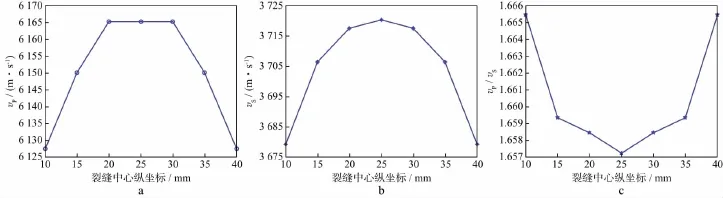
图7 纵波速度(a)、横波速度(b)和波速比(c)随裂缝中心纵坐标变化的曲线
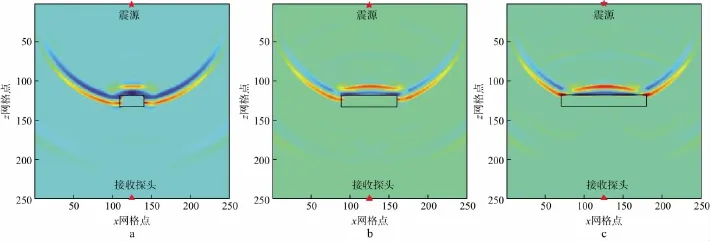
图8 缝长分别为6mm(a),14mm(b)和22mm(c)时的水平分量波场快照
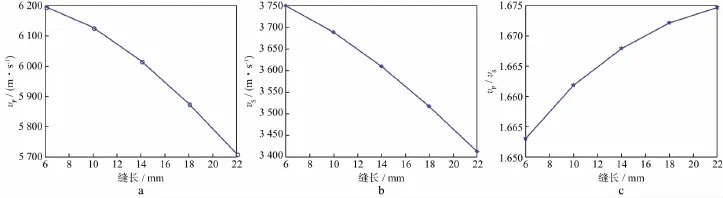
图9 纵波速度(a)、横波速度(b)和波速比(c)随缝长变化的曲线
设裂缝位于岩心模型中心,中心横坐标为25mm,中心纵坐标为25mm,裂缝孔隙流体的含水饱和度为50%,裂缝与水平线之间的倾角为0,缝长为10mm,缝宽分别设置为5,10,15,20,25mm,其中,缝宽为5,15,25mm时质点振动速度水平分量vx在7μs时的波场快照如图10所示。随着缝宽的增加,越来越多的弹性波信号被反射,纵、横波的传播路径变长,接收端纵、横波的初至时间均延后。
纵、横波速度及波速比随缝宽变化的曲线如图11所示,当裂缝位于岩心模型中心时,随着缝宽的增加,纵波速度减小,横波速度减小,波速比增高。
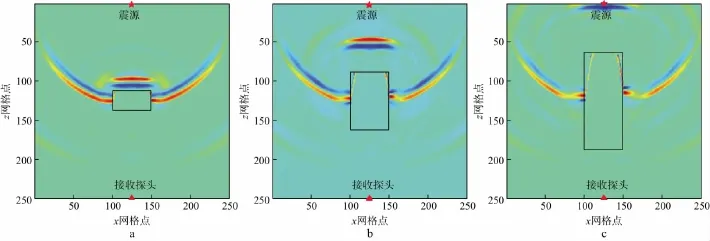
图10 缝宽分别为5mm(a),15mm(b)和25mm(c)时的水平分量波场快照
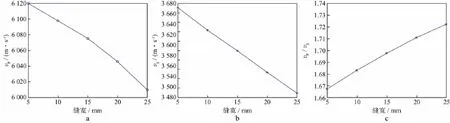
图11 纵波速度(a)、横波速度(b)和波速比(c)随缝宽变化的曲线
5.1.5 裂缝产状对弹性波速度的影响
设裂缝位于岩心模型中心,中心横坐标为25mm,中心纵坐标为25mm,裂缝孔隙流体的含水饱和度为50%,缝长为20mm,缝宽为3mm,裂缝与水平线之间的倾角分别为0,15°,30°,50°,80°和90°。其中,裂缝倾角为30°,50°和80°时质点振动速度水平分量vx在7μs时的波场快照如图12所示。随着裂缝倾角的增加,阻碍弹性波传播的裂缝横截面积减小,纵、横波传播路径变短,接收端纵、横波的初至时间均提前。
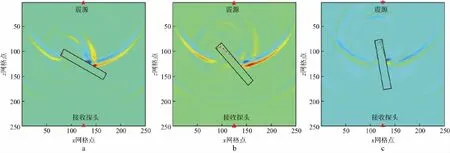
图12 裂缝倾角分别为30°(a),50°(b)和80°(c)时的水平分量波场快照
纵、横波速度及波速比随裂缝倾角变化的曲线如图13所示,随着裂缝倾角的增加,纵波速度增加,横波速度增加,波速比呈增高趋势。
5.2 多裂缝分布对弹性波速度的影响
根据岩样含单裂缝时弹性波速度的模拟结果,当裂缝的分布位置不在震源与接收探头的连线上时,弹性波速度未发生变化。因此对于多裂缝,考虑裂缝均处于震源与接收探头的连线上,不同裂缝数量和裂缝密度的情形。
5.2.1 裂缝数量对弹性波速度的影响
设裂缝均位于岩心模型中心,中心横坐标均为25mm,裂缝孔隙流体的含水饱和度均为50%,缝长均为10mm,缝宽均为3mm,裂缝与水平线之间的倾角均为0,裂缝数量分别设置为1,2,3,4和5。其中,裂缝数量为1,3和5时质点振动速度水平分量vx在7μs时的波场快照如图14所示。随着裂缝数量的增加,纵、横波信号在骨架和裂缝间不断反射,纵、横波的传播路径变长,接收端纵、横波的初至时间均延后。纵、横波速度及波速比随裂缝数量变化的曲线如图15所示,随着裂缝数量的增加,纵波速度减小,横波速度减小,波速比增高。
5.2.2 裂缝密度对弹性波速度的影响
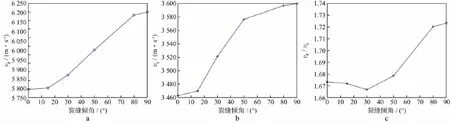
图13 纵波速度(a)、横波速度(b)和波速比(c)随裂缝倾角变化的曲线
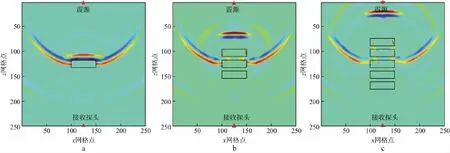
图14 裂缝数量分别为1(a),3(b)和5(c)时的水平分量波场快照
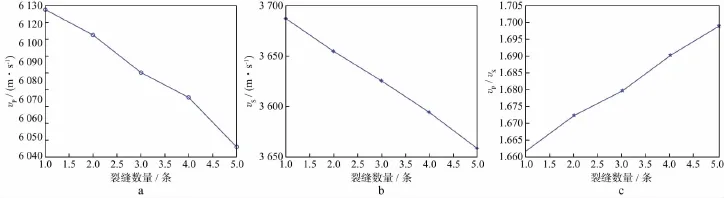
图15 纵波速度(a)、横波速度(b)和波速比(c)随裂缝数量变化的曲线
当孔隙度恒定的情况下,设裂缝均位于岩心模型中心,中心横坐标均为25mm,裂缝孔隙流体的含水饱和度均为50%,裂缝与水平线之间的倾角均为0,缝长均为10mm,缝宽依次为12,6,4,3,2mm,则对应的缝密度分别为条/mm2,其中,缝密度为条/mm2时质点振动速度水平分量vx在7μs时的波场快照如图16所示。随着裂缝密度的增加,组成单个孔隙空间的裂缝尺寸变小,骨架与孔隙之间的界面个数增加,纵、横波在界面之间不断反射、散射,使得纵、横波的衰减增大。纵、横波速度及波速比随裂缝密度变化的曲线如图17所示。随着裂缝密度的增加,纵、横波速度及波速比基本不变。这是因为当孔隙度一定时,尽管裂缝密度发生变化,但是弹性波穿过这些岩样的固体骨架的总时间和裂缝孔隙的总时间不变,因此纵波速度不变。横波受到反射纵波的影响,横波速度略有变化。该结论也与由WYLLIE等[21]提出的计算岩石速度的时间平均模型得到的结果相一致。
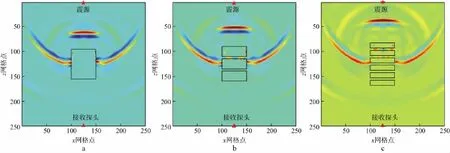
图16 裂缝密度分别为条/mm2(a),条/mm2(b)和条/mm2(c)时的水平分量波场快照
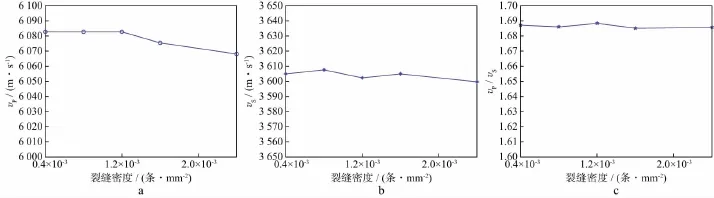
图17 纵波速度(a)、横波速度(b)和波速比(c)随裂缝密度变化的曲线
5.3 含水饱和度对弹性波速度的影响
根据Gassmann方程[22],当气水两相孔隙流体介质的含水饱和度增加时,将使得岩石的纵波速度增加,横波速度略有降低,波速比增高。但这一结论是建立在岩石是均匀各向同性介质的基础上,这里考虑岩样是非均质的情形。
5.3.1 裂缝长宽比小时含水饱和度对弹性波速度的影响
设裂缝位于模型中心,中心横坐标为25mm,中心纵坐标为25mm,水平缝长为20mm,缝宽为3mm,裂缝与水平线之间的倾角为0,裂缝孔隙流体的含水饱和度Sw分别为15%,30%,45%,60%,75%,90%,95%和98%。图18给出了裂缝岩样的含水饱和度Sw分别为30%,60%和90%时质点振动速度水平分量vx在8μs时的波场快照。由图18可以看出,随着含水饱和度的增加,裂缝内流体介质和岩心骨架的声阻抗差距减小,纵、横波的反射减弱,透射增强。
纵、横波速度及波速比随含水饱和度变化的曲线如图19所示。当裂缝的长宽比较小时,随着含水饱和度的增加,纵、横波速度及波速比基本不变。因为当裂缝的长宽比较小时,纵波到达接收端的绕射时间小于其透射时间,在裂缝孔隙形状一定的情况下,纵波绕射的路径不变,纵波速度不变。而横波无法在气 水层中传播,横波的传播路径也不变,但受反射纵波的影响,横波速度略有变化。
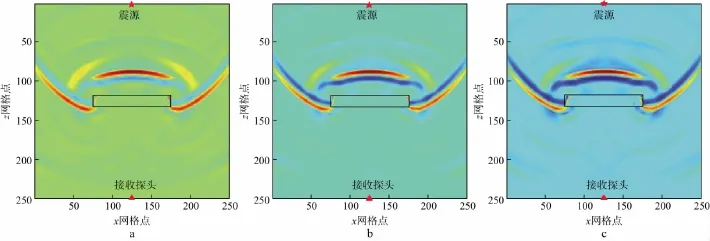
图18 裂缝长宽比小时含水饱和度分别为30%(a),60%(b)和90%(c)时的水平分量波场快照
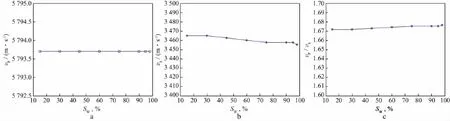
图19 裂缝长宽比小时纵波速度(a)、横波速度(b)和波速比(c)随含水饱和度变化的曲线
5.3.2 裂缝长宽比大时含水饱和度对弹性波速度的影响
设裂缝位于模型中心,中心横坐标为25mm,中心纵坐标为25mm,水平缝长为45mm,缝宽为1.5mm,裂缝与水平线之间的倾角为0,裂缝孔隙流体的含水饱和度分别为15%,30%,45%,60%,75%,90%,95%,98%和100%。图20给出了裂缝岩样的含水饱和度分别为60%,90%和95%时质点振动速度水平分量vx在8μs时的波场快照。
纵、横波速度及波速比随含水饱和度变化的曲线如图21所示。当裂缝的长宽比较大时,随着含水饱和度的增加,纵波速度先缓慢减小而后急剧增加,横波速度则基本不变,纵波到达接收端的透射时间小于其绕射时间。由Wood孔隙流体模量模型可知,由于天然气的体积模量较小,当含水饱和度较高(大于80%)时,随着含水饱和度的增加,混合流体的体积模量将急剧增大,使得纵波速度相应增加。而横波同样无法在气水层中传播,横波的传播路径不变,受反射纵波的影响,横波速度略有变化。
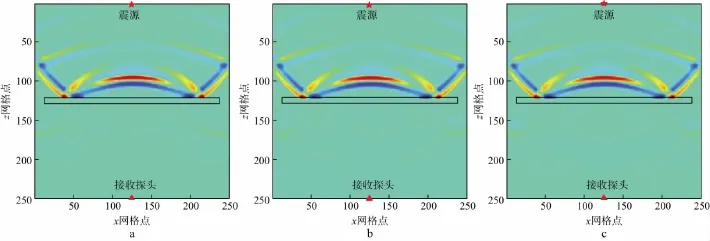
图20 裂缝长宽比大时含水饱和度分别为60%(a),90%(b)和95%(c)时的水平分量波场快照
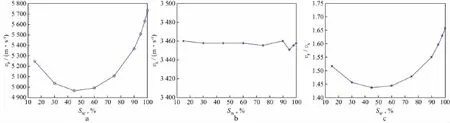
图21 裂缝长宽比大时纵波速度(a)、横波速度(b)和波速比(c)随含水饱和度变化的曲线
6 结论
本文在实验室尺度下对气水两相介质的裂缝模型和弹性波速度开展了较深入的研究,总结弹性波速度与裂缝分布位置、孔隙度、裂缝产状、裂缝密度和含水饱和度之间的变化规律如下。
1)裂缝的分布位置对弹性波速度的影响极大。当裂缝分布不在震源与接收探头间的连线上时,弹性波传播路径不发生更改,纵、横波速度不变。当裂缝分布位于震源与接收探头间的连线上时,弹性波发生绕射,传播路径变长,纵、横波速度减小,且裂缝离震源或接收探头越近,传播路径越长,纵、横波速度越小。
2)岩样的孔隙度与缝长、缝宽和缝数量有关。当裂缝分布位于震源与接收探头间的连线上时,随着孔隙度的增加,纵、横波速度减小,波速比增加。
3)当裂缝分布位于震源与接收探头间的连线上时,随着裂缝与水平线间倾角的增加,纵、横波速度增加,波速比呈增高趋势。
4)当裂缝分布均位于震源与接收探头间的连线上时,在孔隙度一定的情况下,随着裂缝密度的增加,纵、横波速度及波速比基本不变。
5)当裂缝分布位于震源与接收探头间的连线上且裂缝的长宽比较小时,随着含水饱和度的增加,纵、横波速度及波速比基本不变;当裂缝分布位于震源与接收探头间的连线上且裂缝的长宽比较大时,随着含水饱和度的增加,纵波速度会出现最低值,之后纵波速度随着含水饱和度的增加而逐渐增大,横波速度基本不变。
这些规律与认识是对裂缝型岩心样品进行数值模拟分析得出的,如能根据模型介质在几何参数和物理参数满足相似比原理和对应原理的基础上外推到实际地震勘探中,对于指导储层预测、油气检测以及地震资料综合解释都有重要的意义。
[1] 陈乔,刘向君,梁利喜,等.裂缝模型声波衰减系数的数值模拟[J].地球物理学报,2012,55(6):2044-2052
CHEN Q,LIU X J,LIANG L X,et al.Numerical simulation of the fracture model acoustic attenuation coefficient[J].Chinese Journal of Geophysics,2012,55(6):2044-2052
[2] 程超,张树东,潘敏.基于砂岩物理性质变化的声波特性研究[J].天然气工业,2007,27(9):40-43
CHEN C,ZHANG S D,PAN M.The acoustical characteristics research based on the physical property change of the sandstone[J].Natural Gas Industry,2007,27(9):40-43
[3] 房春慧,潘保芝,刘思慧,等.含气饱和度对致密砂岩纵波速度影响的实验研究及应用[J].地球物理学进展,2015,30(4):1673-1676
FANG C H,PAN B Z,LIU S H,et al.Experimental study and application on effect of gas saturation on P-wave velocity[J].Progress in Geophysics,2015,30(4):1673-1676
[4] 印兴耀,李龙.基于岩石物理模型的纵、横波速度反演方法[J].石油物探,2015,54(3):249-253
YIN X Y,LI L.P-wave and S-wave velocities inversion based on rock physics model[J].Geophysical Prospecting for Petroleum,2015,54(3):249-253
[5] 谢月芳,张纪.岩石物理模型在横波速度估算中的应用[J].石油物探,2012,51(1):65-70
XIE Y F,ZHANG J.Application of rock physical model in S-wave velocity estimation[J].Geophysical Prospecting for Petroleum,2012,51(1):65-70
[6] 刘斌,KERN H,POPP T.不同围压条件下孔隙度不同的干燥及水饱和岩样中的纵横波速度及衰减[J].地球物理学报,1998,41(4):537-546
LIU B,KERN H,POPP T.Velocities and attenuation of P-and S-waves in dry and wet rocks with different porosities under different confining pressures[J].Chinese Journal of Geophysics,1998,41(4):537-546
[7] 刘斌,葛宁洁,KERN H,等.不同温压条件下蛇纹岩和角闪岩中波速与衰减的各向异性[J].地球物理学报,1998,41(3):371-381
LIU B,GE N J,KERN H,et al.Velocities and attenuation of P-and S-waves and their anisotropies in serpentinite and amphibolite under different P-T conditions[J].Chinese Journal of Geophysics,1998,41(3):371-381
[8] 曹均,贺振华,黄德济,等.裂缝储层地震波特征响应的物理模型实验研究[J].勘探地球物理进展,2003,26(2):88-93
CAO J,HE Z H,HUANG D J,et al.Seismic responses to fractured reservoirs by physical modeling[J].Progress in Exploration Geophysics,2003,26(2):88-93
[9] 史謌,沈文略,杨东全.岩石弹性波速度和饱和度、孔隙流体分布的关系[J].地球物理学报,2003,46(1):138-142
SHI G,SHEN W L,YANG D Q.The relationship of wave velocities with saturation and fluid distribution in pore space[J].Chinese Journal of Geophysics,2003,46(1):138-142
[10] 朱洪林,刘向君,刘洪.含气饱和度对碳酸盐岩声波速度影响的试验研究[J].岩石力学与工程学报,2011,30(增刊1):2784-2789
ZHU H L,LIU X J,LIU H.Experimental research on effects of gas saturation on acoustic wave velocity of carbonate rock[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S1):2784-2789
[11] 孟召平,张吉昌,TIEDEMANN J.煤系岩石物理力学参数与声波速度之间的关系[J].地球物理学报,2006,49(5):1505-1510
MENG Z P,ZHANG J C,TIEDEMANN J.Relationship between physical and mechanical parameters and acoustic wave velocity of coal measures rocks[J].Chinese Journal of Geophysics,2006,49(5):1505-1510
[12] 未晛,王尚旭,赵建国,等.致密砂岩纵、横波速度影响因素的实验研究[J].石油物探,2015,54(1):9-16
WEI X,WANG S X,ZHAO J G,et al.Laboratory investigation of influence factors on vPand vSin tight sandstone[J].Geophysical Prospecting for Petroleum,2015,54(1):9-16
[13] 尤明庆,苏承东.利用纵波探头测量横波速度的试验[J].岩石力学与工程学报,2003,22(11):1841-1843
YOU M Q,SU C D.Measurement of S-wave velocity with probes for P-wave[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(11):1841-1843
[14] 丁梧秀,王鸿毅,赵文.刻槽法拾取岩样横波波速的试验方法[J].东北大学学报:自然科学版,2009,30(9):1334-1336
DING W X,WANG H Y,ZHAO W.Test method of measuring S-wave velocity of rock by v-shaped groove on specimen[J].Journal of Northeastern University(Natural Science),2009,30(9):1334-1336
[15] VIRIEUX J.P-SV wave propagation in heterogeneous media:velocity-stress finite difference method[J].Geophysics,1986,51(4):889-901
[16] LEVANDER A R.Fourth-order finite-difference P-SV seismograms[J].Geophysics,1988,53(11):1425-1436
[17] 董良国,马在田,曹景忠.一阶弹性波方程交错网格高阶差分法稳定性研究[J].地球物理学报,2000,43(6):856-864
DONG L G,MA Z T,CAO J Z.A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J].Chinese Journal of Geophysics,2000,43(6):856-864
[18] BERENGER J P.A perfectly matched layer for absorption of electromagnetic waves[J].Journal of Computational Physics,1994,114(2):185-200
[19] COLLINO F,TSOGKA C.Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J].Geophysics,2001,66(1):294-307
[20] WOOD A B.A textbook of sound[M].London:Bell &Son Limited,1930:1-519
[21] WYLLIE M R J,GREGORY A R,GARDNER L W.Elastic wave velocities in heterogeneous and porous media[J].Geophysics,1956,21(1):41-70
[22] GASSMANN F.Elastic waves through a packing of spheres[J].Geophysics,1951,16(4):673-685
(编辑:顾石庆)
Numerical simulation of elastic wave velocity in gas-water two-phase rock from fractured model
DUAN Xi1,2,LIU Xiangjun1
(1.Department of Geosciences,Southwest Petroleum University,Chengdu610500,China;2.Department of Science,Southwest Petroleum University,Chengdu610500,China)
Owing to the heterogeneous structure of the core,it is difficult to study the relationship between elastic wave velocity and rock mechanical parameters by means of experiments.And the work of ultrasonic testing is costly and time-consuming.Based on elastic wave theory and Wood pore fluid modulus model,we simulated the elastic wave field in gas-water two-phase rock from fractured model by using staggered grid finite difference method.We also calculated the P-wave velocity,S-wave velocity and wave velocity ratio of the core in the condition of different fracture distribution,porosity,fracture occurrence,fracture density and water saturation.And the effect of these factors on the wave velocity was discussed.The numerical calculation method is simple and its accuracy is high.It has a certain guiding significance in the inversion for rock pore structure by the elastic wave velocity.
elastic wave velocity,wave propagation theory,gas-water two-phase,medium,fracture
P631
A
1000-1441(2017)03-0338-11
10.3969/j.issn.1000-1441.2017.03.004
段茜,刘向君.实验室尺度下气水两相裂缝型介质弹性波速度的数值模拟分析[J].石油物探,2017,56(3):338-348
DUAN Xi,LIU Xiangjun.Numerical simulation of elastic wave velocity in gas-water two-phase rock from fractured model[J].Geophysical Prospecting for Petroleum,2017,56(3):338-348
2016-09-25;改回日期:2017-02-13。
段茜(1981—),女,讲师,博士在读,现主要从事地震岩石物理方面的研究工作。
国家自然科学基金重点项目(51134004)资助。
This research is financially supported by the National Natural Science Foundation of China(Grant No.51134004).

