基于IGOWLA算子的中国粮食生产价格预测研究

赵吉欢，杨桂元，韩孟君

（1.安徽财经大学数量经济研究所，安徽蚌埠233030；2.东北财经大学金融学院，辽宁大连116025）

基于IGOWLA算子的中国粮食生产价格预测研究

赵吉欢1，杨桂元1，韩孟君2

（1.安徽财经大学数量经济研究所，安徽蚌埠233030；2.东北财经大学金融学院，辽宁大连116025）

为探究我国粮食价格波动规律及预测其值，选取2005-2016年中国各季度粮食生产价格数据，首先对其波动性进行描述分析；其次建立一种基于IGOWLA算子的组合预测模型：选择ARMA模型、Holt-Winters乘法模型、残差自回归模型这三种单项预测模型，并通过5种误差评价指标来判断预测模型的效果，结果表明组合预测模型的预测效果较好、准确性较高；接着利用所建立的组合预测模型对2017年各季度粮价进行外推预测，结果表明2017年粮食价格有所上升但相对波动较稳；最后提出政策建议。

粮食价格；ARMA模型；Holt-Winters乘法模型；残差自回归模型；组合预测

粮食价格作为衡量粮食产业发展的核心指标，其稳定性对于我国其他产业发展具有重要支撑作用。我国农业及有关粮食产业政策历来受到国家一以贯之的高度重视。2004-2015年我国连续12年发布以“三农”为主题的中央一号文件；2016年一号文件就加快农业发展方式确保粮食等重要农产品实现有效供给提出若干意见；2017年一号文件提出深入推进农业供给侧结构性改革，同时强调深化重要农产品价格形成机制；前不久举行的中国两会也提出要增强农产品安全保障能力，确保谷物基本自给、口粮绝对安全。

随着这些年国际粮食价格的震荡变化和国内生产状况变化，中国粮食价格波动十分频繁，由图1：2005-2016年粮食价格的无规则波动即可看出。粮价变化对粮农和粮商的生产经营行为造成了很大的干扰，同时由于其价格传导效应对社会整体的物价水平产生较大影响，波及广大消费者基本生活，有碍社会稳定发展。

图12005 -2016年中国粮食价格波动情况

由图1知，2005年前三季度粮食价格持续回落，此期间我国受天气和禽流感影响导致粮食供求市场低迷；但由于我国2005年启动粮食最低价格预案，抑制粮价下跌，故粮价第四季度略有提升；2006-2008年第三季度由于受到世界粮食危机影响，我国粮价总体呈快速上升趋势，局部平稳或略微下降；2006年我国粮食丰收，数量和价格都有所提升，促进了粮食市场发展；2007-2008年第三季度粮食价格保持高位运行，这两年国家加大对粮食生产的支持力度，粮食持续增产，我国粮食市场稳定均衡发展，且受国际粮价涨幅影响，粮价较高；但由于2008年全球金融危机，粮价在第三季度之后大幅下降并在2009年第一季度末跌于谷底；2009年前三季度粮食价格低位运行，这除了与全球经济危机有关，粮食价格自身的周期性规律也发挥了一定作用，此时为粮食新周期的下行阶段。粮食价格的周期大致为七到八年，每一周期均有下降—盘整—上涨—下降阶段。有关研究表明，2008年第二季度末是前一期的结束点。由于我国强劲的国家政策激励，2009年底粮食价格有所提升；2010年由于供求影响及国家政策，国内粮食价格持续上升；2011年之后，我国粮食价格持续稳定下降，这可能是因为粮食价格冲高回落，且自2004年起我国粮食持续增收，粮食市场供给大于需求，在全球经济并不乐观的大背景下，粮食价格将持续走低；2016年第三季度后我国粮食价格有回暖趋势。

一、文献综述

目前有关粮食价格的研究主要集中在粮食价格的波动和影响因素分析，如潘青松[1]通过梳理国内外相关文献探讨了影响粮食价格的因素；胡光瑶[2]通过建立时间序列计量模型分析了国际传导、宏观经济、供需状况、微观个体和信息不对称等因素对粮食价格波动的影响；张萍[3]阐述粮食波动影响因素并提出相应政策建议；张振华[4]对比分析国内外主要农产品价格波动情况，并提出粮价的影响因素和政策建议；高群[5]采用PPM模型分析美国粮食价格突变对国内农业安全的影响。国外学者从生物质能源讨论粮食价格的文献较多，如Tokgoz（2009）[6]分析了石油价格变动先对生物质能源的影响、再对农产品需求和价格产生影响；Chen Sheng-Tung（2010）[7]讨论了石油价格、生物质能和粮食价格的关系。

部分文献对粮食价格进行预测但相对数量较少。孟庆锴[8]根据粮食价格的自相关性采用R/S分析法对未来粮食价格走势进行预测；张婷[9]基于ARIMA模型对大豆价格进行短期预测；喻胜华[10]基于Lasso与支持向量机的串联型、并联型和嵌入型三种组合预测，并将它们运用到我国粮食价格预测中，结果具有更高的预测精度。甘涛[11]在《基于组合预测模型的粮食价格模拟仿真比较》一文构建了粮食价格的加权算数平均组合预测模型，预测结果更贴近实际值；但所采用的加权算数平均组合预测模型过于简单。

基于算子的组合预测模型发展大致如下：Yager[12]在1988年提出了有序加权平均算子（OWA），该算子已被广泛应用于组合预测的研究中；陈华友[13]在2003年提出基于诱导有序加权平均算子（IOWA）的组合预测模型；Yager[14]在2004年将OWA算子拓展成GOWA算子；Merigo[15]在2009年结合诱导变量提出广义有序加权平均算子（IGOWA）；Zhou[16]在2010年给出给出广义有序加权对数平均算子（GOWLA）的定义；江立辉[17]在2015年提出诱导广义有序加权对数平均算子（IGOWLA）的概念并证明其相应性质。目前，在粮食生产价格预测问题上，没有学者采用基于IGOWLA算子的组合预测模型来合理预测粮价波动。

本文首先利用三种单项预测方法各自预测季度粮食价格；随后建立基于IGOWLA算子的最优组合预测模型，并对组合预测的效果进行分析；随后对粮食价格的波动原因进行分析说明。文章数据来源于《中国统计年鉴》，选取2005-2016年粮食生产价格季度数据，如表1所示。

二、各单项预测方法

（一）ARMA模型

表12005 -2016各季度原始数据

自回归移动平均模型（Autoregressive Moving Average Models，ARMA）针对平稳时间序列建模。设平稳时间序列{Xt}是一个ARMA（p，q）过程，即

其中p为自回归阶数，q为移动平均阶数；φ1，…，φp是自回归系数，θ1，…，θq是移动平均系数。

由于ARMA模型要求序列平稳，故首先我们需要对原始的粮食价格序列进行单位根检验判断其平稳性，结果为具有长期趋势的平稳序列，拟合结果为yt=107.736-0.1529·t，参数均显著。对退势后的平稳序列建模。根据自相关、偏自相关函数图及选择模型的三大信息准则，最终建立ARMA（1，3）模型，结果为：

模型估计结果的拟合优度R2=0.85，R2=0.84，F统计量=6.86，其相应概率值=0.01，说明模型整体上显著且拟合效果较好。ARMA（1，3）中AR部分的倒数实根为0.51，在单位圆内；MA部有一个倒数实根两倒数复根，分别为0.83，0.13±0.96i，模都小于1。故认为所估计的ARMA（1，3）平稳且可逆。对此模型进行预测，结果见表2和图2。

（二）指数平滑法

指数平滑法是一种时间序列预测方法，其本质是加权移动平均。指数平滑的目的是通过逐层平滑计算，消除掉随机因素造成的影响，找出预测的基本变化趋势。这里主要介绍Holt-Winters乘法模型（三个参数）的指数平滑法。时间序列yt平滑后的序列y^t由式（3）给出：y^t+k=（at+btk）ct+k（3）

其中：α，β，γ在0～1之间，为阻尼因子；s为季节频率；

预测值计算为：yT+k=（aT+bTk）cT+k-s。其中，aT、bT、T分别表示截距、斜率和样本期末值。

根据Eviews7.0求解出α=1，β=0，γ=0；aT= 96.718，bT=-0.1517；外推四期预测的季节因子分别为c45=0.9982，c46=0.9976，c47=1.0012，c48=1.0029。据此计算出外推四期预测值为y^49=96.397，y^50=96.185，y^51=96.38，y^52=96.391。其余结果由软件自动给出，见表2和图3。

（三）残差自回归模型

残差自回归模型（Auto-Regressive model）：首先对原始数据提取主要的确定性信息：x=Tt+St+εt，式中Tt、St分别为拟合的趋势效应和季节效应。其次，为避免对残差信息的利用不足，进一步检验残差序列{εt}的自相关性。若残差序列没有显著自相关，则可停止对残差序列的分析；否则对残差序列建立自回归模型：εt=μ1εt-1+μ2εt-2+…+μpεt-p+at，式中p是自回归的阶数，at是误差。

本文采用自变量为时间t的幂函数xt=β0+β1t+…+ βktk+εt来拟合趋势效应，拟合结果为xt= 98.261+0.9841t-0.0232t2+εt，各项系数均通过显著性水平为1%的显著性检验。模型回归所得的DW值为0.57，说明残差序列存在自相关性，对残差序列的拟合结果为εt=1.1131εt-1-0.4938εt-2+υt，υt～i.i.dN（0，1）。模型的预测结果见表2和图4。

三、基于IGOWLA算子组合预测模型

设xt（t=1，2，…，n）为原始值序列，分别采用m种单项预测方法对其预测；第i种方法第t时的预测值为xit（i=1，2，…，m；t=1，2，…，n）；w1，w2，…，wm为 m种单项预测方法在组合预测中的权重，有1，wi≥0（i=1，2，…，m）；该指标序列的组合预测值为

定义1设vit为第i种预测方法第t时刻的预测精度，vit∈[0，1]（i=1，2，…，m；t=1，2，…，n）

定义2设m个二维数组（＜v1，a1＞，＜v2，a2＞，…，＜vm，am＞），W=（w1，w2，…，wm）T是和IGOWLAW相关联的加权向量，W满足m）。令

表23 个单项预测模型的预测值及精度（部分结果）

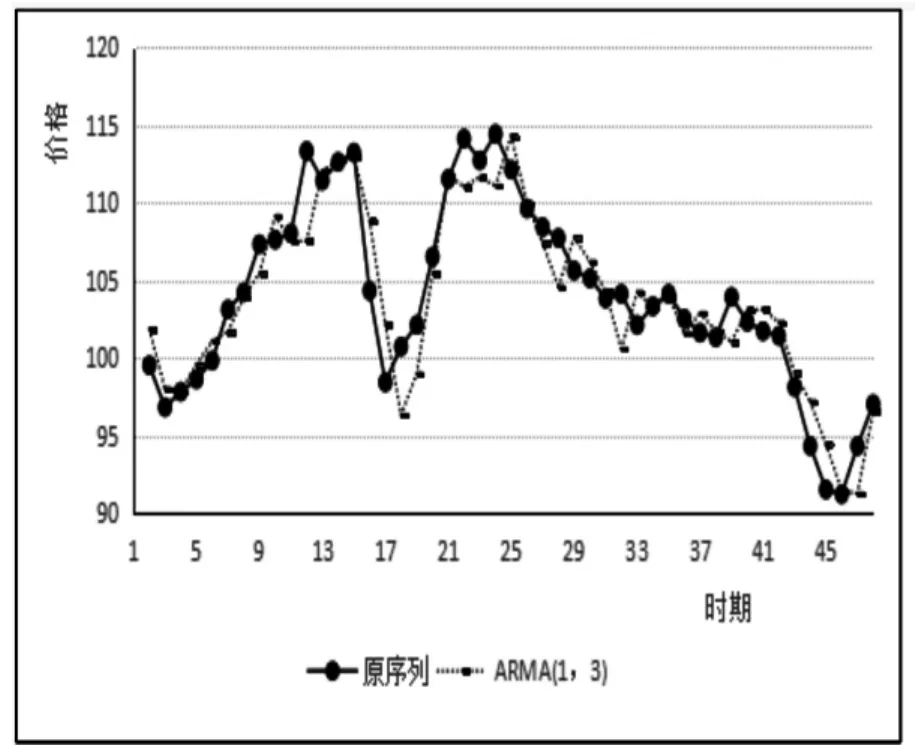
图2 ARMA（1，3）预测值与实际值对照表

图3 指数平滑预测值与实际值对照表

该式中v-index（i）是v1，v2，…，vm中按从大到小顺序排列的第i个大的数所对应的下标，其中v1，v2，…，vm是诱导变量，称IGOWLAW为m维广义诱导有序加权对数平均算子，简称IGOWLA算子。

结合定义1和定义2，若将预测精度vit看作预测值x^it的诱导值，则基于IGOWLA算子的组合测值为：

eit为第i种单项预测方法在t时刻与相应实际值之间的对数λ次幂的预测误差，称E=（eit）m×n为组合预测的对数λ次幂的误差信息矩阵。

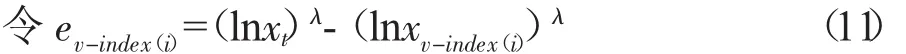
组合预测在t时刻的对数λ次幂的预测误差为：

图4 残差自回归预测值与实际值对照表

图5 组合预测值与实际值对照表

广义诱导有序加权对数平均组合预测n期的预测对数λ次幂误差平方和s为

因此，基于广义诱导有序加权对数平均算子（IGOWLA）的最优组合预测模型为

四、我国粮食生产价格指数的实证研究

（一）模型求解

利用Eviews软件分别求得ARMA（1，3）模型、Holt-Winters乘法模型和残差自回归模型的结果，如表2所示。对式（11）中分别取值为1、2、3计算权重系数，经求解得三种情况权重系数大致相同。本文以λ=3为例进行组合预测，各权重为w1=1，w2=0，w3=0，由此权重系数计算组合预测值及其精度，如表3所示。由于预测季度数较多，考虑到论文结构，此表只列举了2013.1-2016.4的结果。详细的预测情况见图2、3、4、5。

分析表2、表3中的数值可知，虽然这三种单项预测方法的精度较高，但组合预测模型的预测值与真实值最为接近，预测精度最高。为使观察结果更直观，将表2、表3中的各方法预测值与实际值作4张对照图，如图2、3、4、5所示。

（二）评价指标体系

本文选择如下5个误差指标评价基于IGOWLA算子组合预测模型的好坏：

具体评价结果如表4所示：组合预测模型的误差各项指标均显著小于单项预测方法的误差指标，组合预测值更接近真实值，预测效果较好。

5.均方百分比误差：

表3 组合预测值及精度（部分结果）

表4 预测效果评价指标体系

表52017 年前三季度粮食生产价格指数预测值

（三）外推预测

当使用上述组合预测模型预测2017年第一季度至2017年第四季度的粮食生产价格指数，由于无法计算所预测季度的精度，故无法求得最优权重。本文通过查阅相关组合预测的文献，采用多数研究者的处理方法，根据所预测的前48个季度各单项预测方法的平均权重进行预测。各单项预测方法的权重为0.3297，利用这一权重和各单项预测方法的外推预测结果求得我国粮食生产价格指数2017年第一季度至2017年第四季度的组合预测值，如表5所示，2017年第一季度我国粮食生产价格指数有所增加，第二至第四季度略微下降，且总体处于稳定水平。

（四）政策建议

虽然模型的外推预测结果表明2017年我国季度粮食价格总体稳定，但由于影响粮食价格的因素较多，有关部门仍需关注我国粮食价格走势。粮食的供给和需求会直接影响粮食价格的变动，故必须保证粮食市场供需平衡；国际粮价的波动可以通过贸易及价格信息渠道影响国内粮食价格，政府和供应商应密切关注国际粮价并做好应对策略；农业政策保障农民利益，增强农民生产信心，维护我国农业市场及社会稳定，政府应一如既往地重视、落实好农业政策；粮食的期货价格对粮食现货价格的影响日益显著，加强监管农产品期货市场中恶意操纵期货价格行为至关重要。

小结

文章对粮食价格的波动性做了定性和定量分析。首先研究2005-2016年各季度粮食价格数据，结合自然环境、国内外政治经济等信息分析其波动原因，其中国内粮食价格在2006-2008年受世界粮食危机影响高位运行，但2008年的全球金融危机导致2009年粮食价格急剧下降。其次，为了合理预测粮食价格，在三种单项预测模型：ARMA（1，3）模型、Holt-Winters乘法模型和残差自回归模型的基础上，建立基于IGOWLA算子的组合预测模型，结果表明虽然单项预测模型精度较高，但组合预测模型的拟合精度更高、效果更好。接着，为预测粮食价格的未来波动情况，对组合模型外推4季度预测，结果表明2017年第一季度粮食价格提高，但在第二至第四季度略微下降，整体波动较为平缓。虽然模型外推预测结果表明2017年我国季度粮食价格相对稳定，但由于粮食价格波动频繁且影响因素众多，我们提出几点政策建议进一步保障粮价稳定。

[1]潘青松.吴朝阳.国际粮食价格波动对于国内的影响综述[J].价格月刊，2015（4）：10-14.

[2]胡光瑶.基于时间序列的经济计量模型分析农产品价格波动的影响因素[J].财经界，2016（7）：25-26.

[3]张萍.粮食价格波动的影响因素及应对[J].经营管理者，2017（1）：92.

[4]张振华.粮食安全背景下我国粮食价格波动及影响因素分析[J].价格月刊，2016（1）：13-16.

[5]高群，宋长鸣.美国粮食价格突变及其对国内农业安全的启示[J].华南农业大学学报（社会科学版），2016（4）：87-97.

[6]Tokgoz S.The Impact of Energy Markets on the EU Agricultural Sector [J].WorkingPaper，2009，CenterforAgriculturalandRural Development，Iowa State University.

[7]Chen Sheng-Tung，Kuo Hsiao-I，Chen Chi-Chung.Modeling the relationship between the oil price and global food prices[J].Applied Energy，2010（8）：2517-2525.

[8]孟庆锴，梁国岐.基于R/S分析法对粮食价格的预测[J].技术与教育，2015（4）：19-23.

[9]张婷.基于ARIMA模型的国际粮食短期价格分析预测——以大豆为例[J].价格月刊，2016（7）：28-32.

[10]喻胜华，龚尚花.基于Lasso和支持向量机的组合预测及其应用[J].经济数学，2016（2）：46-49.

[11]甘涛.基于组合预测模型的粮食价格模拟仿真比较[J].统计与决策，2016（24）：85-87.

[12]Yager R R.On Ordered Weighted Averaging Aggregation Operators in Multi-criteria Decision Making[J].IEEE Transactions on Systems，Man and Cybernetics，1988，18（1）.

[13]陈华友，刘春林.基于IOWA算子组合预测方法[J].预测，2003（6）：61-65.

[14]Yager R R.Generalized OWA Aggregation Operators[J].Fuzzy Optimization and Decision Making，2004，3（1）.

[15]Merigo J M，Gil-Lafuente A M.The Induced Generalized OWA operator[J].Information Sciences，2009，179（6）.

[16]Zhou L G，Chen H Y.Generalized Ordered Weighted Logarithm Aggregation Operators and Their Applications to Group Decision Making[J].International Journal of Intelligent Systems，2010，25（7）.

[17]江立辉，陈华友，丁芳清，程玲华，赵玉飞.基于IGOWLA算子的最优组合预测模型及应用[J].统计与决策，2015（4）：82-85.

Prediction Research of Chinese Grain Production Price and its Influencing Factors

ZHAO Ji-huan1，YANG Gui-yuan1，HAN Meng-jun2
（1.Institute for Quantitative Economic Research，Anhui University of Finance&Economics，Bengbu，Anhui 233030；2.Finance School，Dongbei University of Finance and Economic，Liaoning，Dalian 116025）

In order to explore the law of Chinese grain price fluctuation and its influencing factors，first we choose quarterly grain price data from 2005 to 2016 and analysis it.Then，a combined prediction method based on the induced generalized ordered weighted logarithmic averaging operator is proposed.We use the ARMA model，the Holt-Winters multiplication model and the residual autoregressive model respectively to make an individual prediction of Chinese grain production price.Then，we establish the combination forecasting model based on IGOWLA operator.By comparison，it is found that the latter has higher accuracy and stronger predictive ability than the former．Next，we obtain the weights under the basement of the IGOWLA operator and make predictions and analysis to the grain production price from the first quarter of 2017 to the fourth quarter of 2017.Last，we make some suggestions.

grain price；the ARMA model；the Holt-Winters model；the residual autoregressive model；combination forecasting model

F201

A

1671－9743（2017）04－0031－06

2017-03-01

国家社科基金项目“组合预测模型与方法创新及其优化理论研究”（12BTJ008）；安徽财经大学研究生科研创新基金项目（ACYC2016115）。

赵吉欢，1993年生，女，浙江诸暨人，硕士研究生，研究方向：数量经济学；杨桂元，1957年生，男，安徽萧县人，教授，研究方向：数量经济学；韩孟君，1993年生，男，浙江诸暨人，硕士研究生，研究方向：金融工程。