丝维尔纤维基本力学性能研究
李福顺,李显波
(青岛大学纺织服装学院,山东青岛 266000)
丝维尔纤维基本力学性能研究
李福顺,李显波
(青岛大学纺织服装学院,山东青岛 266000)
为研究丝维尔纤维的力学性能,采用不同的实验方案对丝维尔纤维和普通粘胶纤维的基本力学性能进行测试分析。
丝维尔纤维 力学性能 力学模型
智能空调纤维制品与传统纤维制品的区别在于保温机理不同。传统衣物主要是通过热隔绝来实现保温,而智能空调纤维能为人体提供舒适“微气候环境”的全新保温机理,能够热调节而不仅仅是热隔绝。目前生产智能空调纤维的方法有填充法[1-2]、纺丝法[3-4]和微胶囊法[5-9],不同的方法生产出的纤维性能会有一定的差别。由于其智能的调温性能和优良的可纺性,使其在家居用品、服装、生物医疗用品和汽车内饰等领域被广泛应用。
丝维尔纤维是一种功能化的粘胶纤维,是利用了相变调温材料技术的高科技产品[10]。该纤维性能优良,以其拥有的蓄热放热双向调节功能而成为了用途广泛的纺织材料。本文采用的是微胶囊法制备的纤维材料,针对其力学性能进行研究,包括丝维尔纤维在干态和湿态下的断裂强力,结节和钩接等状态下的强力与伸长的关系,并与普通的粘胶纤维进行对比,最后建立了力学模型对纤维力学性能进行分析。
1 实验
丝维尔纤维(1.67dtex,38mm,河北),粘胶纤维(1.67dtex,38mm,山东),LLY-06型电子式单纤维强力仪(山东)。
1.2 实验设计
实验前将纤维放置在标准大气状态(温度20℃,相对湿度65%)下预调湿48个小时。在实验时,应在标准温湿度条件下进行。根据纤维本身特点,本实验选用10mm/min的拉伸速度,将夹持距离设置为10mm,并给予纤维150mg的预加张力,使纤维伸直而不伸长。纤维的形态分别为干态、湿态和钩接打结,在上述条件下,测试20次,得到纤维强伸性能的相关数据。
2 实验结果及分析
2.1 拉伸断裂性能的测试
2.1.1 拉伸断裂性能基本指标
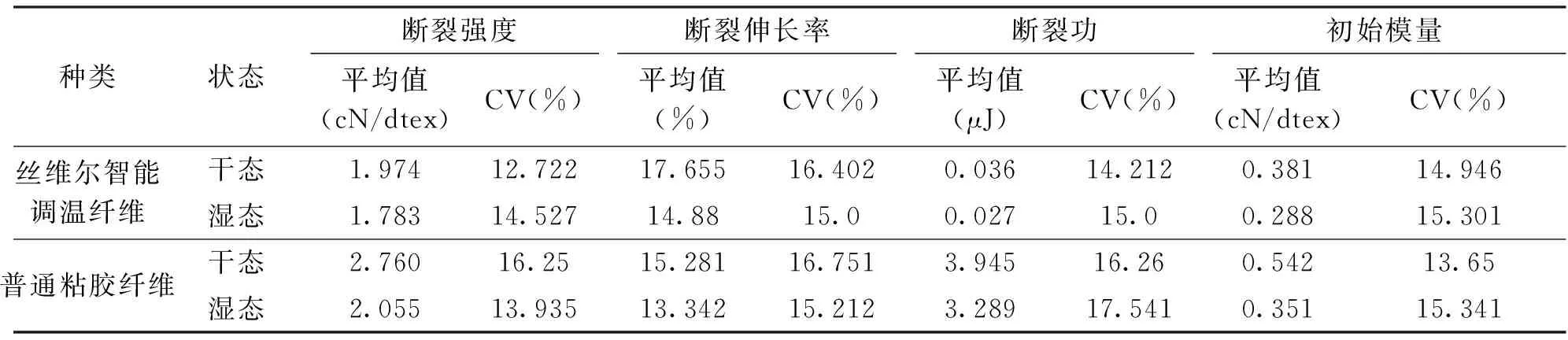
表1 丝维尔纤维和普通粘胶纤维在干态和湿态下的断裂强度
2.1.2 拉伸曲线
“谢谢你们的好意。陈老师昨天也和我说,叫我不要担心下学期的学费和生活费问题。我想好了,上大学后我就勤工俭学。”
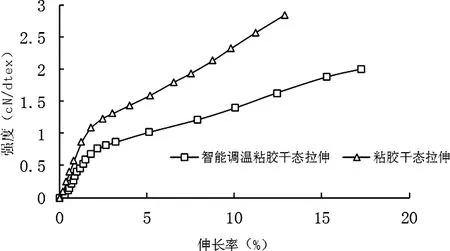
图1 两种纤维干态拉伸曲线
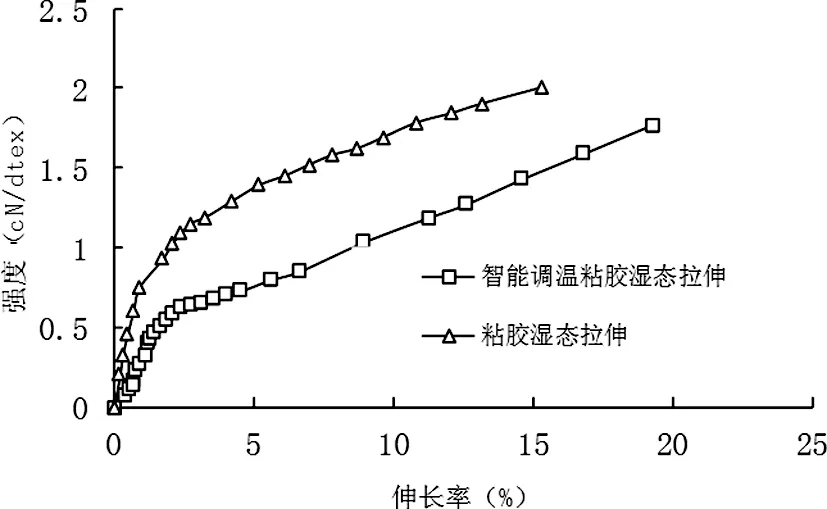
图2 两种纤维湿态拉伸曲线
从以上实验结果分析来看,从图1、图2可以得出:在一次拉伸断裂性能测试时,常温干态和湿态下丝维尔智能调温粘胶纤维都比普通粘胶纤维的拉伸断裂强力低;还可以得出丝维尔智能调温粘胶纤维的初始模量比普通粘胶纤维的也要小。
从纤维的内部结构分析,纤维内部结晶区所占比例越大,纤维大分子排列紧密区也越大,纤维大分子排列越均匀,紧密程度越大,在拉伸实验中,纤维的断裂强力越大。从实验结果来看,在纺丝维尔智能调温粘胶纤维过程中,在其纺丝液中所加入的智能调温微胶囊分子改变了纤维的内部结构,使纤维内部的结晶区部分减少,增大了其无定型区所占的比例,大分子排列更加疏松,从而在拉伸试验时丝维尔智能调温粘胶纤维无论是在干态下还是在湿态下都比普通粘胶纤维的断裂强力低。
从图1、图2对比可以看出:从干态到湿态实验条件下,丝维尔智能调温粘胶纤维的初始模量的降低程度较普通粘胶纤维的下降程度小。初始模量是指纤维受拉时抵抗小变形的能力。初始模量越大,在拉伸断裂曲线图上所表现的曲线的接近直线部分的斜率越大,则表明纤维的刚性越好,反之初始模量小,则刚性小,纤维的伸长大。由两种纤维的干湿态初始模量的下降程度可以得出:丝维尔智能调温粘胶纤维的尺寸稳定性较普通粘胶纤维的要好,从而改善了普通粘胶纤维的一部分缺点。
2.2 不同夹持方式对纤维断裂性能的影响
两种纤维在不同夹持方式下的断裂性能指标如表2。

表2 粘胶纤维和丝维尔智能调温纤维在不同夹持方式下的拉伸性能
2.2.1 拉伸曲线
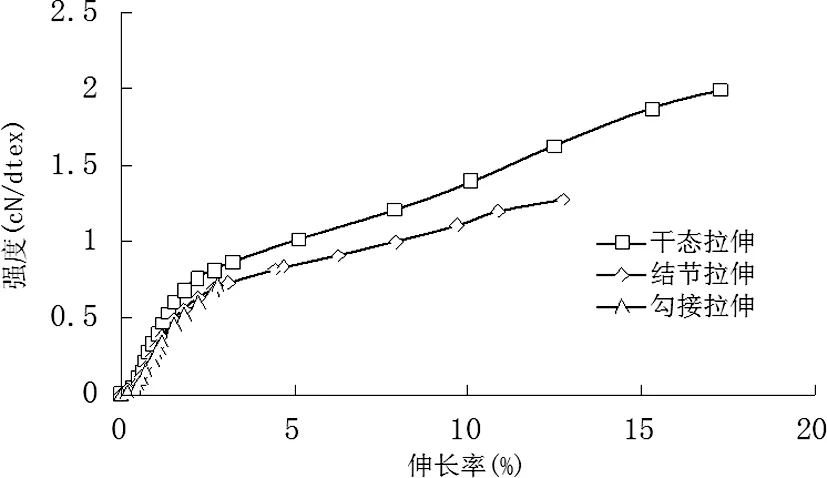
图3 在不同夹持方式下丝维尔智能调温粘胶纤维的拉伸曲线
由图3、图4可以看出,丝维尔智能调温粘胶纤维在结节、钩接拉伸状态下的断裂强度均比直接拉伸状态的断裂强度小。
从以上实验结果可以得出:丝维尔智能调温粘胶纤维在结节和钩接拉伸状态下均比其在干态下自然拉伸时的断裂强力低,可能原因是由于钩接和打结导致纤维弯曲,当纤维所受的拉伸力尚未达到纤维断裂所需的拉伸力时,在搭接处和打结处的纤维出现相抵滑移,使得纤维的伸长率超过无状态下的断裂伸长率而导致纤维的弯曲折断[11]。另外,丝维尔智能调温粘胶纤维的初始模量的下降程度不明显,总体来说丝维尔智能调温粘胶纤维的尺寸稳定性好。
从图4可以得出:普通粘胶纤维在干态拉伸时的断裂强力比钩接和结节拉伸时都要高,而且干态拉伸的初始模量介于钩接拉伸和结节拉伸的初始模量之间,整体上普通粘胶纤维的初始模量的变化程度较丝维尔智能调温粘胶纤维的大,普通粘胶纤维的尺寸稳定性比丝维尔智能调温粘胶纤维的差。
由此说明,使用丝维尔智能调温粘胶纤维不仅能够在一定条件下调节温度,还可以改善普通粘胶纤维尺寸稳定性差的缺点,从而提高了纤维的使用价值。
2.3 丝维尔智能调温粘胶纤维力学模型的建立与分析
2.3.1 力学模型的建立
为了对丝维尔智能调温粘胶纤维的拉伸曲线进行模拟,我们采用了不同的粘弹性力学模型,包括:Vangheluwe模型[12-13]、改进的Vangheluwe模型[12,14]、Zurek模型[12,15]、改进的Zurek模型[12,16]。
Vangheluwe模型由一模量为C的非线性弹簧及弹性模量为M线性弹簧和粘滞系数为η的牛顿粘壶串联组成的麦克斯韦尔模型串联组成[17],其力学模型表达式为:
P(ε)=P0+A(1-exp(-Bε))+Cε2
其中A=ηγ,B=M/A,C为非线性弹簧的模量。
为了能够更好地描述纤维的力学性能,在Vangheluwe模型中用εD替换ε,用 εE替换ε2,以此将Vangheluwe模型改进,得到最终的力学模型表达式:
P(ε)=P0+A(1-exp(-BεD))+CεE
其中:A=ηγ,B=γ/T,C为εE的函数,D、E为指数。
Zurek模型中含有一惯性摩擦系统,它先并联于一个由牛顿黏壶和虎克弹簧组成的系统,然后整体再串联于另一虎克弹簧[17],其力学模型表达式:
P(ε)=Aε+B+(Cε-B)exp(-aε)
用εD将ε替换后,Zurek模型得到改善,可得到最终的力学模型表达式:
P(ε)=Aε+B+(Cε-B)exp(-aεD)
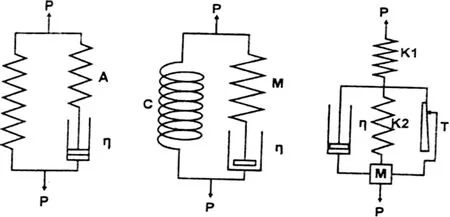
a标准线性固体模型 b Vangheluwe模型 c Zurek 模型
图5 力学模型
2.3.2 不同夹持方式下的丝维尔智能调温粘胶纤维的拉伸模型及拟合参数
用Vangheluwe模型及其改进模型、Zurek模型及其改进模型对拉伸曲线进行模拟。用origin8.0软件拟合拉伸模型得到的最佳拟合参数见表3
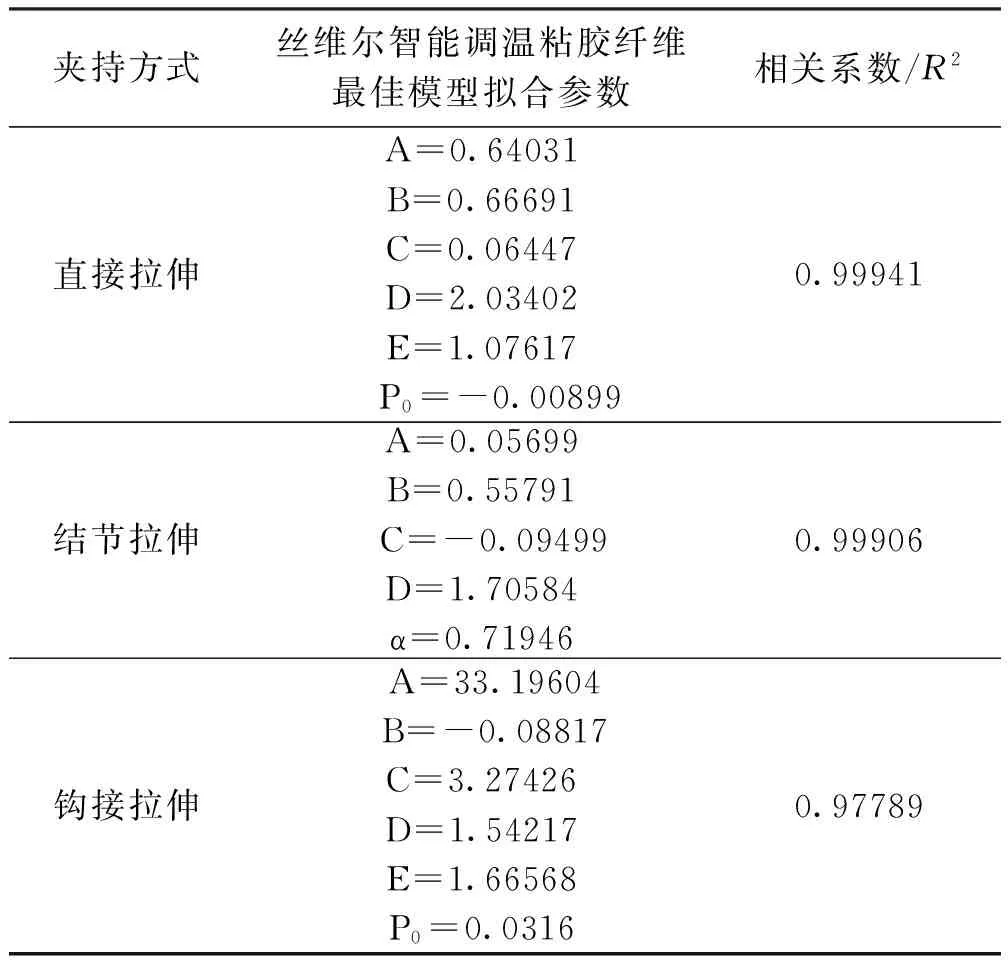
表3 不同夹持方式下的拟合的最佳参数
从表3 origin8.0拟合曲线参数可以看出,不同的夹持方式下,所选用的最佳模型不同。丝维尔智能调温粘胶纤维在直接拉伸和钩接拉伸状态下的最佳的拟合模型都是改进的Vangheluwe模型,而在结节拉伸状态下的最佳的拟合模型是改进的Zurek模型。
由表3看出,拟合的相关系数在0.97和0.99以上,说明这个模型很适合来模拟丝维尔纤维和普通粘胶纤维的力学性能,初始预加张力为负值,可能原因是由于仪器的问题,对纤维的初始预加张力不够引起的。
3 结论
(1)丝维尔纤维断裂强度无论在干态和湿态都要低于普通粘胶纤维,但是其在湿态断裂强度的下降强度反而降低,这说明丝维尔纤维能够很好地改善普通粘胶纤维在湿态下强度低的缺点。
(2)丝维尔纤维无论在干态还是湿态下,其初始模量都要低于普通粘胶纤维,通过初始模量的损失率,我们能够看出调温纤维的刚性较大,因此我们也能看出其尺寸稳定性要好于普通粘胶纤维。
(3)丝维尔纤维的抗弯曲性能在结节和钩接状态下要略低于普通粘胶纤维。
[1] 李新娥. 空调纤维的研发及应用[J]. 纺织科技进展,2008(2):18-19.
[2] 王艳怡. 空调纤维及其针织物的性能研究[D]. 河北科技大学,2009.
[3] 张琳琳. 空调纤维及其混纺针织物的染整工艺研究[D]. 石家庄:河北科技大学,2009.
[4] 刘行燕,王跃存. 腈纶空调纤维织物产品设计与织造工艺研究[J]. 轻纺工业与技术,2013(6):17-20.
[5] 张世春. 微胶囊法封装相变储能材料研究进展[C]// 中国化学会全国无机化学学术会议,2015.
[6] 于伟东,章悦庭,段武海,等. 动物蛋白外包覆的相变储能微胶囊、制备方法及其用途:CN 1715359 A[P]. 2006.
[7] 于京现,李子荣,鲍学忠. Method for spinning blended yarns with outlast air-conditioning fibers/Newdal fibers: CN 101982583 B[P]. 2011.
[8] Bryant Y G,David C P.Fibers with reversible enhanced thermal storage properties and fabrics made there form:US.4756958[P].1988-07—26.
[9] 赵连英,董卫东,杜维强,等. Outlast空调纤维开发智能调温毛衣的实践[J]. 现代纺织技术,2010,18(6):42-43.
[10]于林海. 丝维尔智能调温黏胶纤维的性能研究[J]. 针织工业,2008(10):11-15.
[11]姚穆.纺织材料学[M].北京:中国纺织出版社,2009.1.
[12]杨庆斌,李克让,刘逸新,等. 大豆蛋白复合改性纤维的力学性能[J]. 纺织学报,2006,27(10):70-73.
[13]杨庆斌. 大豆蛋白改性纤维的理化性能及混纺比优化的研究[D]. 上海:东华大学,2005.
[14]Aksan,S.,and Zurek,W. A Rheological Model of Viscose Rayon,J. Appl. Polym. Sci. 19,3129-3137(1975).
[15]Tao,M.,and Postle,R. Viscoelastic Analysis of Keratin composite,Part I: Longitudinal and Transverse Mechanical Properties,Textile Res. J.,59 (3),123-138 (1989).
[16]Zhang P,Liu X F,Sun C P. An quantum approach of measurement based on the Zurek's triple model[J]. Physics,2002.
[17]杨庆斌,李克让,赵堂英,等.大豆蛋白改性PVA纤维力学性能建模研究[J],青岛大学学报(工程技术版),2006(2):68-72.
2016-11-16
李福顺(1990-),男,硕士研究生,研究方向:功能纺织品。
TS101.92+1
A
1008-5580(2017)02-0144-04

