纬编与经编织物线圈建模与仿真分析

邓中民，张 勇

(1.武汉纺织大学纺织科学与工程学院， 湖北武汉 430200； 2.武汉纺织大学数学与计算机学院， 湖北武汉 430200)



纬编与经编织物线圈建模与仿真分析

邓中民1，张 勇2

(1.武汉纺织大学纺织科学与工程学院， 湖北武汉 430200； 2.武汉纺织大学数学与计算机学院， 湖北武汉 430200)

分别探讨了纬编线圈和经编闭口线圈的结构，建立了相应的数学模型，在VC++平台下进行仿真分析，并在此基础上设计出较为复杂的织物效果。综合阐述了纬编和经编线圈的建模原理，为织物生产设计及进一步仿真提供了思路。实验表明：建立的模型曲线平滑，能形象地表达线圈的真实客观形态。

纬编 经编 线圈结构 几何模型 仿真

0 引言

随着计算机仿真技术的不断完善与发展，计算机在各行各业中的应用也越来越广泛和深入。在纺织服装行业中，主要体现在数字化纺织CAD/CAM系统以及纺织机械的自动化控制等方面，通过计算机进行辅助设计，从而简化设计过程。

在进行针织物的仿真中，首先需要对组织中的线圈进行数学建模。线圈是针织物最基本的组成单元，要实现对织物较好的仿真效果，首先便需要对织物中的线圈进行数学建模。

对线圈结构的几何形状进行研究并非是线圈本身的意义决定，而是因为这些线圈在经过相互串套后，可以形成各种组织结构的针织物。可以说线圈形态对织物结构起着决定性的作用。本课题在对线圈的研究中，并不是针对线圈的真实形态，而是针对线圈的几何形态而言的。

针织物中的线圈结构是因织物的种类不同而不同的，纬编织物中的线圈主要包括圈柱、圈弧和沉降弧，与之相比，经编织物的线圈结构则要复杂得多。如图1所示为线圈的几何形态，(a)为纬编线圈，(b)中分别为经编闭口和开口线圈。为了对线圈建模有全面的认识和把握，本文分别对纬编和经编线圈进行建模。

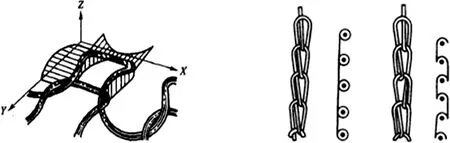
(a)纬编线圈 (b)经编线圈

1 纬编线圈

在纺织行业中纬编的历史悠久，纬编以其产品的应用广泛性一直稳占市场。随着人们生活质量的提高，人们对花型的多样性和精美程度提出了更高的要求。因而对其进一步深入分析，也显得十分重要。纬编针织物纱线走向是横的，如我们普通的袜子，织物是通过织针在横列方向上编织出上下彼此联结的线圈横列所形成[1]。于是某一横列的所有线圈都是由一根纱线编织而成的。

1.1 纬编线圈的建模

通过对皮尔士(Pierce)和芒登(Mumde)模型的比较，本文主要以皮尔士模型为基础。需要注意的是，在VC++中，坐标是以原点向右(x轴)与向下(y轴)逐渐增大分布的，由一个半圆、两个1/4圆与两条直线构成，建立如下数学模型，如图2所示：

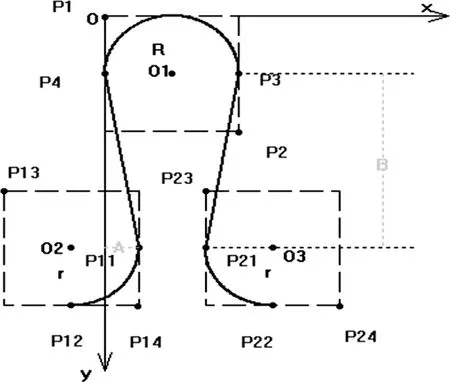
图2 基于皮尔士模型的纬编线圈建模

建立坐标系后，各点坐标如表1与表2所示。

表1 模型中各点坐标

表2 模型中各点坐标

在MFC中的使用CDC绘图工具类进行我们的绘图操作，主要执行程序是：

POINT P1={x0+0*b,y0+0*b};POINT P2={x0+2*R*b,y0+2*R*b};

POINT P3={x0+2*R*b,y0+R*b};POINT P4={x0+0*b,y0+R*b};

POINT P11={x0+A*b,y0+(R+B)*b};

POINT P12={x0+(A-r)*b,y0+(R+B+r)*b};

POINT P13={x0+(A-2*r)*b,y0+(R+B-r)*b};

POINT P14={x0+A*b,y0+(R+B+r)*b};

POINT P21={x0+(2*R-A)*b,y0+(R+B)*b};

POINT P22={x0+(2*R-A+r)*b,y0+(R+B+r)*b};

POINT P23={x0+(2*R-A)*b,y0+(R+B-r)*b};

POINT P24={x0+(2*R-A+2*r)*b,y0+(R+B+r)*b};

根据上述定义的点，进行直线的绘制，执行程序如下：

dc.MoveTo(P11.x,P11.y); dc.LineTo(P4.x,P4.y);

dc.MoveTo(P21.x,P21.y); dc.LineTo(P3.x,P3.y);

然后进行圆的绘制，包括半圆与1/4圆，执行程序如下：

dc.Arc(P1.x,P1.y,P2.x,P2.y,P3.x,P3.y,P4.x,P4.y);

dc.Arc(P13.x,P13.y,P14.x,P14.y,P12.x,P12.y,P11.x,P11.y);

dc.Arc(P23.x,P23.y,P24.x,P24.y,P21.x,P21.y,P22.x,P22.y);

1.2 纬编线圈的仿真分析

线圈的建模工作，是实现花纹仿真设计的前提，在上文建模工作顺利完成后，接下来将进行常见的花纹与特殊花纹结构的模拟仿真。如下图所示，经过循环操作后，可以得到图3(a) 所示的平纹花纹组织。通过改变模型中控制点的连接方式以及简单修改坐标可以得到图3(b)所示的平针-移圈花纹和图3(c)所示的罗纹空气层花纹。对于其他复杂花纹组织如挑花、绞花、扳花、嵌花等都可以用这种方式仿真出来。

通常的，为了方便复杂花型的仿真设计，我们一般可以用矩阵Amn的形式表示整个花纹效应。其中不同的数字αij代表不同的走纱方式，于是在后续设计中，我们只需确定其结构编织图的数字表示，因而数字的正确排列关系到整体的美观效果。

(1)

VC++环境下，我们使用二维数组的形式来表示上述矩阵Amn，例如图3(a),图3(b),图3(c)可分别用如下矩阵表示：

int a[6][6]={{1,1,1,1,1,1},{1,1,1,1,1,1},{1,1,1,1,1,1},

{1,1,1,1,1,1},{1,1,1,1,1,1},{1,1,1,1,1,1}};

int b[8][9] = {{1,1,1,1,1,1,1,1,1},{1,2,1,1,2,1,1,2,1},

{1,1,1,1,1,1,1,1,1},{1,1,1,1,1,1,1,1,1},

{1,2,1,1,2,1,1,2,1},{1,1,1,1,1,1,1,1,1},

{1,1,1,1,1,1,1,1,1},{1,2,1,1,2,1,1,2,1}};

int c[5][5] = {{1,1,1,1,1},{4,3,4,3,4},{1,1,1,1,1},

{4,3,4,3,4},{1,1,1,1,1}};

(a)平针花纹 (b)平针-移圈花纹 (c) 罗纹空气层花纹

2 经编线圈

关于经编线圈结构的研究一直以来已经进行了几十年，在此期间，也形成了诸多的线圈建模方法。主要有：G.L.Allison(G.L.安立逊)的简化模型、P.Grossberg(P.格罗斯勃)第一模型和P.Grossberg(P.格罗斯勃)第二模型。但这些方法计算复杂，结果与实际存在一定的误差。

2.1 Bezier曲线

Bezier曲线是在计算机图形学及CAD中最常用的一种曲线，有良好的几何性质,能简洁、完美地描述和表达自由曲线曲面。只需将一个控制点进行升降,就可完成曲线的升降，计算非常方便，Bezier 曲线是很好的曲线拟合工具[2]。

因而对于经编织物仿真，采用Bezier样条曲线来实现纱线弯曲的拟合是十分合适的，本文主要利用Bezier曲线的特点，只需将确定线圈的各点坐标连接起来，进而可以实现基本单元的模拟。对于给定空间n+1个点的位置矢量Pi(i=0,1,2,…,n)，则Bezier曲线的表达式为[3]：

(2)

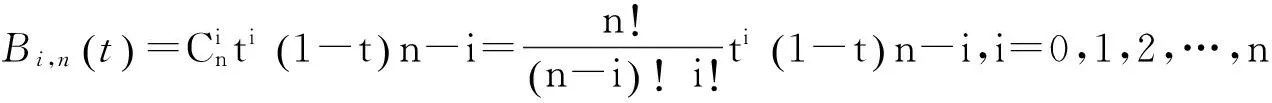
常见的当n= 3时，Bezier曲线为属于四阶三次曲线，曲线方程为：

(3)

这时只需给定四个点P0、P1、P2、P3(第一个点和第四个点是端点，曲线经过端点，另两个点是控制点)，就可唯一确定其形状，如下图4所示。

图4 Bezier 曲线

2.2 经编线圈建模

编链组织通常用于窗纱等装饰织物的地组织，它既可以作为一种地组织单独使用，还可与压纱和衬纬组织结合使用，构成各种形态的网格组织，进而设计出各种花型组织。

如上图1(b)所示，分为开口编链和闭口编链，其都是通过线圈的循环得到。本节主要对闭口线圈进行建模，通过对经编针织物中线圈形态结构的分析，本节建立如图5所示的模型。如下图5所示，我们用绿色、红色和蓝色三段Bezier曲线的组合形成经编闭口线圈模型，其中每段Bezier曲线都为四阶三次曲线，即由4个点控制生成。其中绿色和红色部分是对称的，主要模拟圈干和针编弧，用蓝色部分模型延长线，形成闭口线圈。如表3所示，我们给出了绿色部分控制点的坐标信息。

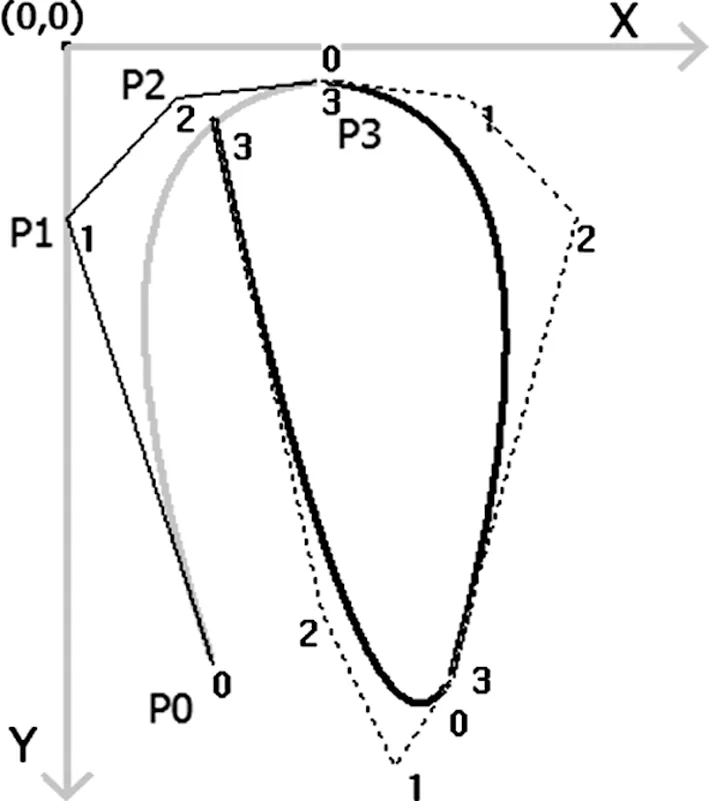
图5 经编闭口线圈模型

表3 左边绿色部分各点坐标

2.3 经编线圈的仿真

在完成经编闭口线圈建模的基础上，通过x和y方向的循环可得如图6(a)所示的闭口编链组织，可以看出仿真效果良好，曲线光滑流畅。依然使用Bezier曲线的方式，继续仿真了几种具有代表性的地组织结构，如图6(b)所示是我们常见的经平组织以及图6(c)所示的双梳节变经平网眼组织，该组织多用于鞋面网眼设计[4]。从下图6的仿真结果可以看出，效果较为真实。目前，编链和六角网眼是多梳花边中最常用的两种地组织。下面我们将主要讨论六角网眼地组织。

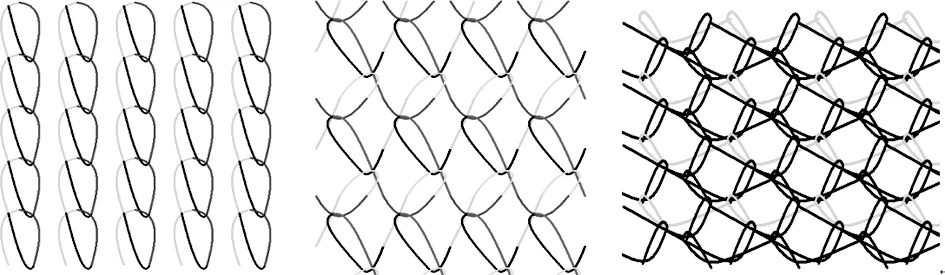
(a)闭口编链 (b)经平组织 (c)双梳节变经平网眼

2.4 六角网眼地组织

六角网眼地组织柔软性较好，具有不脱散性，通常花边织物多采用六角网眼地组织，因此应用非常广泛。不同横列数的完全组织可形成不同风格的六角网眼，本节将以最常见的三横列六角网眼为例进行仿真探讨[5]。其垫纱数码为：

GB1: 2-0/0-2/2-0/2-4/4-2/2-4//

GB2: 0-0/2-2/0-0/4-4/2-2/4-4//

根据纱线在织物中的实际形态，首先确定其完全组织，即最小循环单元，指经过横向和纵向的循环可以形成整体的织物。本节建立的六角网循环单元模型如图7(f)所示。

这里我们只对GB1进行仿真，并依次详细地给出了垫纱仿真图。如图7(a)、(b)所示依次形成开口线圈，然后在图7(c)中形成闭口线圈,接着跨到另一列，完成类似操作。考虑到六角网眼的对称性，因而可以简化我们的建模。通过观察图7(c)和图7(f),可知图7(c)经过平移和镜面变换即可以得到图7(f)所示效果，从而简化了建模过程。

(a)GB1:2-0/;(b)GB1: 2-0/0-2/;(c)GB1: 2-0/0-2/2-0/

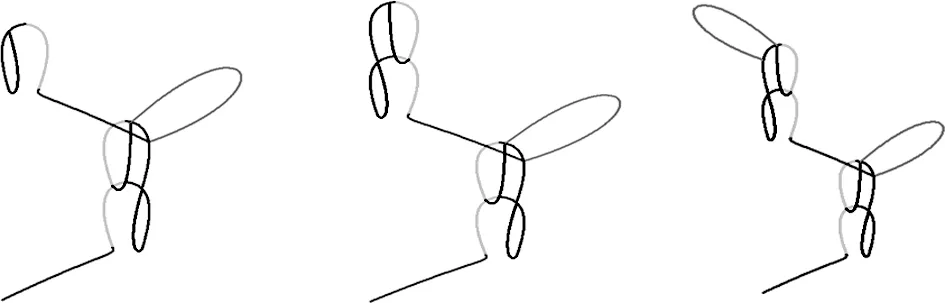
(d)GB1: 2-0/0-2/2-0/2-4/;(e)GB1: 2-0/0-2/2-0/2-4/4-2/;(f) GB1: 2-0/0-2/2-0/2-4/4-2/2-4//

图7 走纱图

六角网眼的数学模型建立后，我们就可以得到图7(f)的循环单元，确定各个控制点坐标后，列出相应的方程，同时在x和y两个方向进行循环，即可形成整体连续的效果，仿真图如图8所示。从仿真图我们可以看出，仅有GB1即可以形成六角地网，但有的边仅有一根纱线，为了加固以及均匀平整，于是加了GB2。由于GB2模型较为简单，在此我们不做讨论。

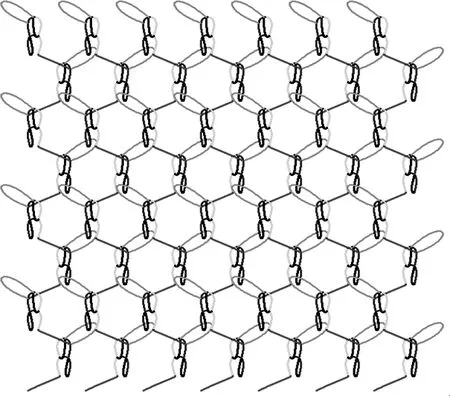
图8 六角网仿真效果

3 结束语

利用计算机辅助设计、制造，使传统的纺织服装行业面临更大的机遇与挑战。线圈是针织物的基本结构单元，本文在Visual C++的环境下，通过建立相关的数学模型，实现了针织线圈的仿真。采用两种不同的建模方式,分别对纬编和经编线圈进行建模，使对线圈建模原理有了全面的把握。在此建模思想的指导下，进行了其他一些简单花型的仿真，并取得了较好的仿真效果。

本文所采用的线圈模型是理想状态下的线圈几何结构模型，而在实际情况下，线圈会因为受力不平衡而产生一定程度的倾斜，且不同组织结构的织物，其线圈倾斜程度也有一定的差异。在后期的研究中，要根据经验确定线圈倾斜角度的统计关系，并将其结果加入计算机仿真程序，能够使织物的仿真效果图更加逼近织物的真实状态。

[1] 王辉,方园,潘优华.纬编针织物线圈模型的分析与研究[J]. 浙江理工大学学报,2008(5):521-525.

[2] 陈立亭,邓中民,严平,刘童花. 经编贾卡织物的一种仿真方法[J]. 武汉科技学院学报,2007(2):10-13.

[3] 王田田,邓中民,李华,王学文. 贾卡针织物的仿真建模[J]. 武汉科技学院学报,2009(3):8-12.

[4] 张勇,孙永陪. 经编间隔织物运动鞋面料工艺设计[J]. 成都纺织高等专科学校学报,2015(3):97-100.

[5] 李华,邓中民. 多梳经编地组织的计算机仿真[J]. 针织工业,2009(9):15-17.

Loop Modeling and Simulation Analysis of Weft and Warp Knitting Fabric

DENGZhong-min1,ZHANGYong2

(1. College of Textile Science and Engineering,Wuhan Textile University,Wuhan 430200; 2.College of Mathematics and Computer Science,Wuhan Textile University,Wuhan 430200)

The structure of weft loop and warp knitting closed loop was explored respectively and corresponding mathematical model was established. Simulation analysis was done by VC++ platform. Based on it,more complex fabric patterns were designed. The modeling principles of weft and warp knitting loop were comprehensively elaborated,which provided a thought for fabric design and further simulation. The results showed that the model had a smooth curve which could express the real objective form of the loop.

weft knitting warp knitting loop structure geometric model simulation

2016-05-22

国家自然科学基金项目(11071280)，湖北省重大科技项目，纺织面料及服装数字化设计与制造成套技术研究(C2010036)。

邓中民(1964-)，男，教授，博士生导师，研究方向：纺织CAD系统的设计与应用。

TS 941.2

A

1008-5580(2017)02-0037-05