基于频域内动力XFEM和人工蜂群算法反演结构内部缺陷
王珍兰 江守燕 杜成斌 储冬冬 陈艳丽
(1. 江苏省水利科学研究院, 江苏 扬州 225002; 2. 河海大学 力学与材料学院, 南京 210098)
基于频域内动力XFEM和人工蜂群算法反演结构内部缺陷
王珍兰 江守燕 杜成斌 储冬冬 陈艳丽
(1. 江苏省水利科学研究院, 江苏 扬州 225002; 2. 河海大学 力学与材料学院, 南京 210098)
结合频域内动力扩展有限元(Extended Finite Element Methods,XFEM)与人工蜂群(Artificial Bee Colony,ABC)算法的优点,建立了反演结构内部缺陷的数值模型.阐述了动力XFEM的基本公式,给出直接滤频法迭代求解结构自振频率的过程.在迭代过程中,ABC智能算法通过整体和局部共同搜索,能够迅速地得到最优解,并可有效地避免陷入局部最优,XFEM通过水平集函数表征不连续区域,迭代过程中数值计算网格不需要进行重剖分.结合XFEM与ABC算法所建立的反演模型有效地减少了迭代的计算成本.采用频域内结构的前若干阶频率作为真实响应,考虑了惯性力影响,比静力响应只考虑劲度的变化更全面.结果表明:所建立的反演结构内部缺陷的数值模型能够准确地识别出结构内部单个缺陷的位置和大小.
动力扩展有限元法; 人工蜂群算法; 直接滤频法; 孔洞; 反演分析
近年来,发展的结构无损检测技术主要有:超声波法、红外成像法、电磁热效应、雷达法、声发射技术等[1].由于工程结构的复杂性,目前这些无损检测方法的结果受结构几何边界条件(尺寸)、试验条件(设备)、材料均匀性条件以及计算机模型工作量的限制,只能对结构物局部进行检测,很难给出整体结构中缺陷的准确形状、位置分布等[2].结构的动力特性(频率、振型)和动力响应与结构物理参数(如质量、刚度、阻尼等)是紧密相关的,当结构产生损伤时,这些内在的物理参数将或多或少的发生变化,必将引起结构振动特性的改变[3].基于结构振动特性,对结构内部的缺陷进行识别,与局部检测方法相比,可全面的对结构进行检测,且操作简单快捷,不影响结构正常使用[4],其可行性已得到室内试验的验证[5-7].
反演分析模型由正分析过程及目标函数极小化迭代两部分组成.对于含缺陷结构的正分析问题是一类典型的不连续问题,扩展有限元法(Extended Finite Element Methods,XFEM)是目前处理不连续问题的最有效数值方法,它在包含不连续界面的单元内,通过改进标准有限元法的位移场近似函数来捕捉其不连续性,XFEM能够有效地解决结构包含孔洞、夹杂和裂纹等缺陷的数值模拟问题[8-9],在反分析问题的领域也显示出了极大的优势[10-14].
文中结合动力XFEM和人工蜂群(Artificial Bee Colony,ABC)算法的优点,重点研究反演结构内部缺陷(夹杂)的数值模型,阐述动力XFEM的基本公式,给出直接滤频法迭代求解结构自振频率的过程.最后,通过数值算例验证所建立的反演数值模型.
1 反分析问题
为确定孔洞、裂缝等缺陷在结构内部所处的位置及其大小,需要通过一些智能优化算法,建立适当的参数模型,并将计算得出的结构关键点响应值与其相应的实测值进行对比,使二者间误差最小.
模型中的参数可以由向量表示为
(1)
式中,n为模型中待求参数总个数.
对于结构内的圆形缺陷,其参数可表示为
(2)
式中,(xc,yc)、rc分别为圆形缺陷的圆心坐标和半径.
参数模型的目标函数可表示为
(3)
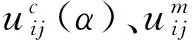
因此,该反分析问题可描述为:通过智能算法进行搜索迭代,直至寻找一组最佳的参数
(4)
且
(5)
实现目标函数式(3)最小化.其中,αmax和αmin分别为待求参数的上、下限值.
2 动力问题的扩展有限元法
2.1 水平集函数
对于圆形缺陷,其水平集函数为
(6)
式中,xc、rc分别为缺陷的圆心点坐标向量和半径.
在数值模型中仅储存单元结点的水平集值,即φi=φ(xi),单元内部的水平集值需要通过插值得到
(7)
式中,Ni(x)为常规有限元中结点i的插值形函数.
2.2 位移模式
采用动力扩展有限元法计算含缺陷结构的动力响应(频率)的估计值,其单元的位移模式可表示为
(8)

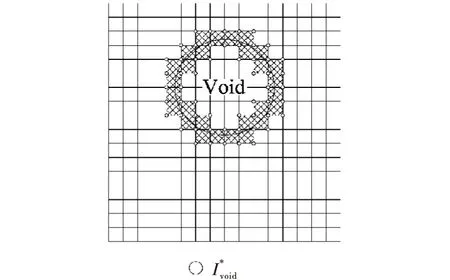
图1 扩展有限元改进结点
2.3 支配方程
根据扩展有限元法单元的位移模式(8),利用虚功原理,忽略阻尼,可推导出动力问题的扩展有限元法的支配方程

(9)
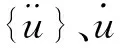
3 直接滤频法
在动力平衡方程式(9)中,令{f}为0,便得到结构自由振动方程,在工程实际中,阻尼对结构自振频率和振型的影响极小,可略去其影响,故得到无阻尼系统的自由振动方程为
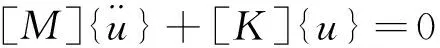
(10)
假定结构作自由振动时,其各点均作简谐振动,且振动频率与初相角一致,而振幅不同,则结点的位移列阵为
(11)
式中,{u0}为单元结点的振幅列阵,即振型;ω是圆频率;θ是初相角.
将式(11)代入式(10),可得广义特征方程
(12)
上式{u0}有非零解的充分必要条件是系数矩阵行列式为0,即
(13)
解之可得n个实频率,n为结构自由度总数.
文中仅需求解结构若干阶低频率,故采用直接滤频法进行迭代求解.采用直接滤频法求第j个特征值及其特征向量的具体步骤如下:
1)给出初始迭代向量和计算常数
(14)
2)第k次迭代时,先计算各振型的滤频系数
(15)
3)计算第k次迭代的特征向量近似值
(16)
当j=1时等号右端第二项为0.
4) 由Rayleigh商求第k次迭代的λj近似值
(17)
5) 检查特征值是否满足精度
(18)
若精度满足要求,则迭代停止,否则重复式(15)至式(18).
4 人工蜂群算法
将人工蜂群算法引入动力扩展有限元法中,搜索最优参数解.人工蜂群算法的控制参数主要包括三个:蜜源的总数(NFood)、蜜源花蜜量不变时的蜂群最大搜索次数(Limit)和蜜蜂群的最大搜索总数(NIter).在该算法中,蜜源的位置即为反问题中待求的可行解(缺陷的位置、大小),蜜源的花蜜量为其可行解的效益(适应度函数值),这使得算法的空间复杂度较低,蜜蜂群搜索花蜜的速率可视为可行解的优化速率,蜜源的最大花蜜量即为优化问题的最优解.可行解的适应度函数值f(α)与目标函数值O(α)的相互关系为
(19)
基于人工蜂群算法进行蜜源(式(6)中水平集函数的缺陷参数)搜索,根据蜜源的实时情况,由动力扩展有限元法计算得出结构频率,并与结构实测频率进行对比,得出当前蜜源的花蜜量,即该蜜源的“收益度”.当由搜索到的蜜源计算得出的花蜜量小于允许误差时,即确定结构内部缺陷的具体分布及尺寸.人工蜂群算法的具体求解过程为:
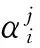
(20)
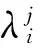

(21)
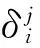
3)观察蜂搜索阶段.观察蜂根据采蜜蜂种群处蜜源花蜜量大小选择一个采蜜蜂,并在其邻域内同样进行新蜜源位置的搜索,并按照与采蜜蜂相同的规则更新其位置.观察蜂选择采蜜蜂种群处蜜源的概率计算公式为
(22)
4)侦察蜂搜索阶段.当某采蜜蜂陷入某蜜源的局部最优,即搜索Limit次后,领域内仍然没有搜索花蜜量更佳的蜜源时,该采蜜蜂放弃当前蜜源位置成为侦察蜂,其位置更新到由式(26)在蜜源空间内生成新蜜源处.
5 数值算例
图2(a)为含圆形孔洞的简支梁示意图,梁的长度为400 mm,宽度100 mm.数值计算时,假设简支梁处于平面应变状态,简支梁被离散成20×80的均匀网格,如图2(b)所示.基体的弹性模量E=22 GPa,泊松比ν=0.167.真实结构的前5阶频率值暂由XFEM数值计算得到.

图2 简支梁尺寸示意图及XFEM计算网格/mm
为验证研制的程序的正确性,将XFEM结合直接滤频法计算得到的简支梁前5阶振型与商业软件ABAQUS的有限元计算结果进行比较,如图3所示,(a1)~(e1)为XFEM计算结果,(a2)~(e2)为ABAQUS计算结果.可以看出,采用研制的程序计算得到的简支梁前5阶振型与ABAQUS计算结果吻合较好,从而验证了研制的程序的正确性.

图3 含一孔洞简支梁的前5阶振型图
本算例中,圆形孔洞有圆心坐标(xc,yc)和圆的半径rc,共3个待求参数.反演过程中,取蜜源的总数NFood=100,蜜源花蜜量不变时的蜂群最大搜索次数Limit=20,蜜蜂群的最大搜索总数NIter=300.待反演参数的限值为xc∈[0 400],yc∈[0 100],rc∈[0 50].图4中,给出了圆形孔洞半径分别为5 mm、10 mm及15 mm时缺陷的反演过程,从图中可以看出,建立的反演分析模型能够较为准确地探测出缺陷的大小和位置.

图4 基于实测前5阶频率的单个圆形孔洞的反演过程
6 结 论
结合频域内动力XFEM和ABC智能优化算法的优点,建立了反演结构内部缺陷的数值模型.阐述了动力XFEM的基本公式,给出直接滤频法迭代求解结构自振频率的过程.文中采用频域内结构的前若干阶频率作为真实响应,考虑了惯性力影响,比静力响应只考虑劲度的变化更全面.结果表明:所建立的反演结构内部缺陷的数值模型能够准确地识别出结构内部单个缺陷的位置和大小.
[1] Hola J, Bien J, Sadowski L, et al. Non-destructive and Semi-destructive Diagnostics of Concrete Structures in Assessment of Their Durability[J]. Bulletin of the Polish Academy of Sciences Technical Sciences, 2015, 63(1):87-96.
[2] Robert B. New NDT Techniques for New Materials and Applications[J]. Assembly Automation, 2012, 32(3):211-215.
[3] 朱宏平, 余 璟, 张俊兵. 结构损伤动力检测与健康监测研究现状与展望[J]. 工程力学, 2011(2):1-11.
[4] Wahalathantri B L, Thambiratnam D P, Chan T H T, et al. Vibration Based Baseline Updating Method to Localize Crack Formation and Propagation in Reinforced Concrete Members[J]. Journal of Sound & Vibration, 2015, 344:258-276.
[5] Bui Q B, Mommessin M, Perrotin P, et al. Assessing Local-scale Damage in Reinforced Concrete Frame Structures Using Dynamic Measurements[J]. Engineering Structures, 2014, 79:22-31.
[6] Wu A L, Yang J N, Loh C H. A Finite-element Based Damage Detection Technique for Nonlinear Reinforced Concrete Structures[J]. Structural Control And Health Monitoring, 2015, 22:1223-1239.
[7] Pesic N, Zivanovic S, Dennis J, et al. Experimental and Finite Element Dynamic Analysis of Incrementally Loaded Reinforced Concrete Structures[J]. Engineering Structures, 2015, 103:15-27.
[8] Jiang S Y, Du C B, Gu C S, et al. XFEM Analysis of the Effects of Voids, Inclusions, and Other Cracks on the Dynamic Stress Intensity Factor of a Major Crack[J]. Fatigue & Fracture of Engineering Materials & Structures, 2014, 37:866-882.
[9] Jiang S Y, Du C B, Gu C S. An Investigation Into the Effects of Voids, Inclusions and Minor Cracks on Major Crack Propagation by Using XFEM[J]. Structural Engineering and Mechanics, 2014, 49(5):597-618.
[10] Chatzi E N, Hiriyur B, Waisman H, et al. Experimental Application and Enhancement of the XFEM-GA Algorithm for the Detection of Flaws in Structures[J]. Computers and Structures, 2011, 89(7-8):556-570.
[11] Jung J, Jeong C, Taciroglu E. Identification of a Scatterer Embedded in Elastic Heterogeneous Media Using Dynamic XFEM[J]. Computer Methods in Applied Mechanics & Engineering, 2013, 259:50-63.
[12] Sun H, Waisman H, Betti R. A Multiscale Flaw Detection Algorithm Based on XFEM[J]. International Journal for Numerical Methods in Engineering, 2014, 100:477-503.
[13] Nanthakumar S S, Lahmer T, Rabczuk T. Detection of Flaws in Piezoelectric Structures Using Extended FEM[J]. International Journal for Numerical Methods in Engineering, 2013, 96:373-389.
[14] 江守燕, 杜成斌. 基于扩展有限元的结构内部缺陷(夹杂)的反演分析模型[J]. 力学学报, 2015(6):1037-1045.
[责任编辑 周文凯]
Identification of Internal Defect by Using Dynamic Extended Finite Elememt Methods in Frequency Domain and Artificial Bee Colony Algotithm
Wang Zhenlan Jiang Shouyan Du Chengbin Chu Dongdong Chen Yanli
(1. Jiangsu Province Water Conservancy Science Research Institute, Yangzhou 225002, China;2. College of Mechanics and Materials, Hohai Univ., Nanjing 210098, China)
This paper proposes an approach for detecting an internal defect by using dynamic extended finite element method(XFEM) in frequency domain and the artificial bee colony (ABC) algorithm. The basic formulation for dynamic XFEM is given. And then the direct filtration of frequencies for solving iteratively the natural frequency of vibration is elaborated. The main advantage of the proposed approach is that the ABC algorithm can effectively avoid the appearance of the local optimum by the global and local searching strategy and the XFEM alleviates the need for remeshing the domain with level set methods used to describe the discontinuous region at each iteration process. The inverse model combined XFEM with ABC algorithm can effectively reduce the amount of calculation for inverse analysis. Compared with the static response, it is more comprehensive for the several order frequency in the frequency domain which is used as the real response considering the effect of inertia force. The results show that the proposed approach can effectively detect the location and shape of the internal defect in materials.
dynamic extended finite element methods; artificial bee colony algorithm; direct filtration of frequencies; void; inversion analysis
2017-01-10
国家自然科学基金(51579084);江苏省水利科技项目(2015030, 2016017)
王珍兰(1958-),女,高级工程师,主要从事水利工程建设质量管理与检测研究.E-mail:jsslzj@163.com
10.13393/j.cnki.issn.1672-948X.2017.03.004
O302
A
1672-948X(2017)03-0015-05

