某火箭弹发射车定向管支撑刚度对炮口干扰的影响研究

高立强

摘要：本文针对工程实际应用，建立实用性较强的发射车力学模型，研究火箭弹的出口干扰。该模型通过简单的地面静力学试验获得发射管的6个自由度的支撑刚度，将这6个刚度函数直接引入通用的多刚体计算模型中进行仿真计算。并以某火箭弹为例，对不同支撑刚度和不同火箭弹推力下的火箭弹出口干扰进行了研究。

关键词：火箭弹；定向管；支撑刚度；炮口干扰

1引言

某火箭弹发射车的火箭弹散布直接影响到弹药作用效能，是重要的战技指标。影响火箭弹散布的主要原因之一是炮口干扰，即火箭弹离开炮口时刻的姿态变化（主要是偏航与俯仰方向的角度）。多管火箭发射车定向器的作用是支撑与导向火箭弹，但是定向管在火箭弹推力作用下又构成了对火箭弹出口姿态的干扰，所以如何根据火箭弹推力选择发射车的支撑刚度至关重要。

定向管一般安装在发射车上的摇架上，摇架固定在回转机上，而回转机又固定在底架上，底架通过支腿和轮胎与地面接触，发射车依靠自重和摩擦力与地面保持一定的连接。这样，整个发射车就构成了一个复杂的弹性结构。

南京理工大学的芮筱亭教授考虑了发射车弹性支撑[1]，并假设弹体和定向管为刚性，根据动特性试验采用传递矩阵法获得整车的结构弹性和质量特性，然后进行弹性支撑下发射动力学计算，得到了较准确的计算结果。

2力学模型

假设发射车与地面之间不会发生相对位移，不失一般性，定向管通过一个6自由度弹簧连接在地面上，弹簧上有6个不同的弹性函数：三个移动位移刚度函数和三个转动位移的刚度函数，之所以称之为函数，是因为刚度往往是位移的函数，即是非线性的。

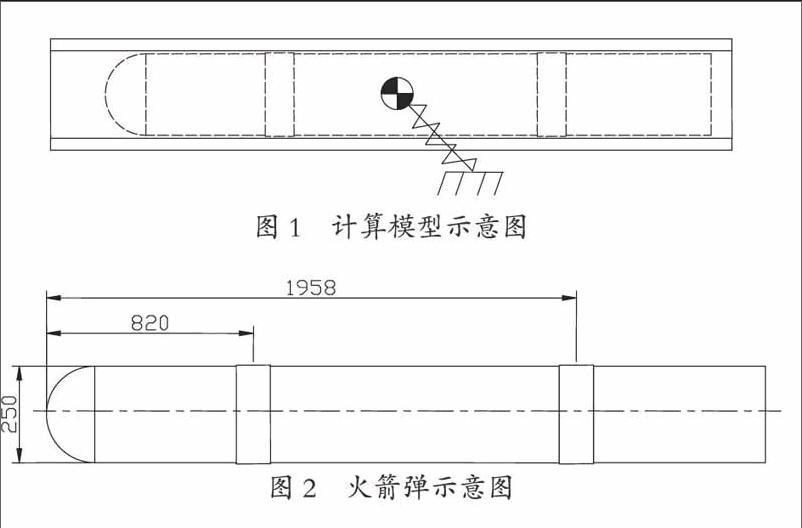
如图1所示，定向管是根据图样建立的纯刚性的三维模型，火箭弹也是根据图样建立的纯刚性的三维模型。火箭弹与定向管之间只有接触关系，即定向器与火箭弹定心部和导向钮之间的接触。数学模型如式2.1，该方法建立的力学模型在动力学仿真软件或动力学求解程序中均可以进行解算，即采用通用的龙阁库塔法求解动力学微分方程。火箭弹等效模型的外形尺寸见图2。

式中：

Mj——质量分布矩阵；

vj——位移向量；

Cj——阻尼矩阵；

Kj——内里作用位置矩阵；

fj——外力矩阵。

数值仿真模型的假设和初始状态：

a. 火箭弹和定向管均为刚体；

b. 火箭弹和定向管的相互摩擦设定为钢和钢之间的油摩擦，其中静摩擦系数取0.08，动摩擦系数取0.05，接触刚度100kN/mm；

c. 运动0点时，火箭弹导向钮位于定向管螺旋导槽的起始位置，定向管导槽呈水平状态；

d. 射角设定为45°。

3力学模型计算精度对比验证

为了验证计算模型的正确性和计算精度，将本文的简化力学模型与全刚性、全弹性的模型对比。计算是以准弹体坐标系为输出坐标系，轴向为弹轴方向，法向为过弹轴的铅垂面的向上方向，横向符合右手定则。

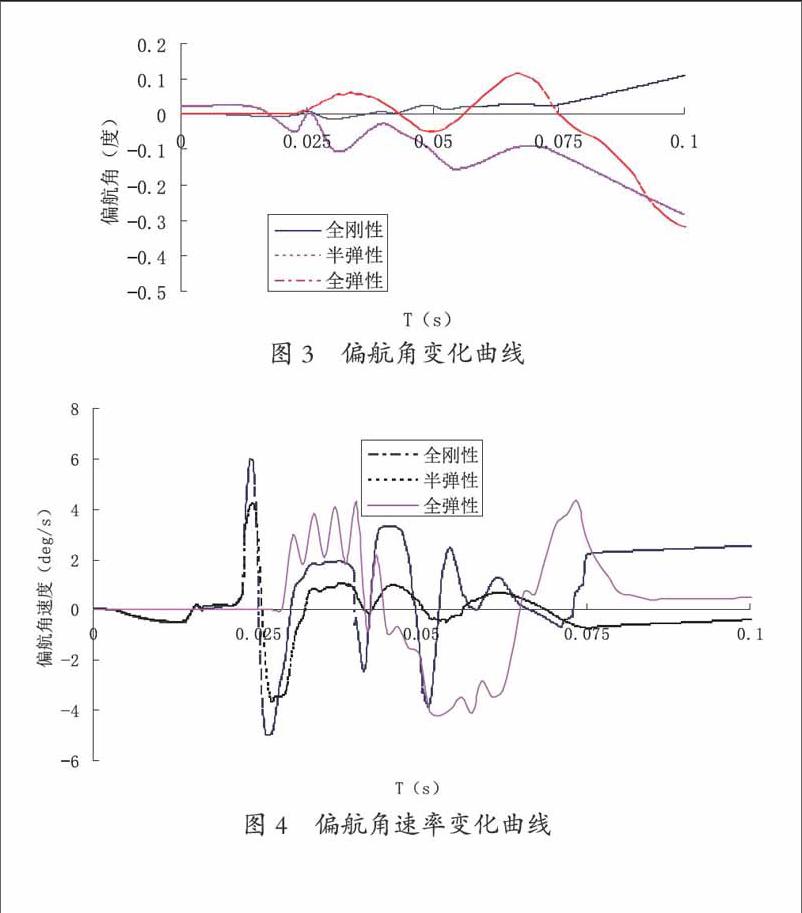
火箭弹在定向管内的运动和出口的姿态可以由火箭弹的角运动来表征，考虑到弹在管内运动的随机性，本文调整了初始偏差量（弹炮相对位置和动不平衡量）进行多次仿真，仿真结果（如上页图3、图4）。图中，半弹性模型为本文采用的简化模型。

火箭弹发射过程中，偏航角不受重力影响，所以表征定向管对火箭弹的干扰。图3和图4对比了三种力学模型的火箭弹管内和出口时的偏航角和偏航角速率，可以看出：弹性支撑主要以发射车的弹性支撑影响为主，发射管和火箭弹的弹性对出口干扰的影响较小。

通过三种模型的对比分析可知，半弹性和全弹性模型计算结果接近，即简化的半弹性模型的计算精度可以满足工程应用。

4计算结果与分析

根据验证后的简化力学模型对不同支撑刚度（俯仰和回转）和不同火箭弹推力下的发射管偏航角度和俯仰角度进行了对比分析。由于火箭弹的出口偏航角度和俯仰角度与定向管差别很小，可以忽略不计，所以文中不给出火箭弹的偏航角度和俯仰角度随支撑刚度（俯仰和回转）和发动机推力的变化曲线。

以某型28管火箭发射车为例，计算边管（1号管）发射时的初始扰动。如图5所示，1号管位于定向束的最左边和最上面，相对回转中心距离最大，在发动机推力最用下最容易发生角位移。

计算了3种不同回转与俯仰支撑刚度下定向器偏航角和俯仰角（即射向和射角），刚度2为静力试验获得的发射车实际回转与俯仰支撑刚度，刚度1为10倍的实际回转与俯仰支撑刚度，刚度3为0.1倍的实际回转与俯仰支撑刚度。火箭弹推力为该型多管火箭发射车配装的模型火箭弹的实际推力，计算结果如图6和图7所示，图8为实际发射过程中的射向变化曲线，图9为实际发射过程中的射角变化曲线。

对比图6、图7、图8和图9可知，文中仿真计算出的火箭弹出口时刻（70ms～80ms）的定向器射角、射向变化量接近，说明该计算模型可以较为准确的计算出火箭弹的出口扰动。由图6可知，当支撑刚度较小时，定向器在火箭弹的推力作用下发射偏转，导致火箭弹离轨时的偏航角和俯仰角偏离预设值，这将导致28根定向管发射车出去的火箭弹具有不同的射角、射向，进而影响火箭弹的散布。

根據发射车的实际支撑刚度对不同火箭弹推力下的火箭弹出口扰动进行分析，其中，推力2为该型发射车配装的模型火箭弹的实际推力，推力1为实际推力的0.7倍，推力3为实际推力的1.3倍。计算结果如图10和图11所示，由图可知，当火箭弹的推力较小时，出口时刻定向器的射角、射向偏差较小。

6结论

为了达到仿真计算和研究发射车，建立种简化的多管火箭弹发射力学模型（半弹性支撑模型），通过与全弹性支撑模型对比认为，该模型计算精度满足工程设计要求。采用该模型，以某型火箭发射车及其配装的某型火箭弹为例，对不同火箭弹推力下发射车定向器支撑刚度对火箭弹的出口扰动的影响进行了仿真研究。对比仿真计算结果与试验结果说明了计算模型的正确性，通过对比不同火箭弹推力和不同发射车定向管支撑刚度下的火箭弹出口扰动发现，火箭弹的推力和发射车的定向器支撑刚度都会影响火箭弹出口偏航角和俯仰角，导致不同定向器发射出去的火箭弹具有不同的初始参数，进而影响火箭弹的散布。所以，针对多管火箭武器系统应该进行系统匹配性优化，选取最优的火箭弹推力曲线，同时，在条件允许的情况下可以对多管火箭弹的边管射击诸元进行必要的修正，以获得更好的火箭弹散布。

参考文献：

[1]芮筱亭，陆毓琪. 多管火箭发射动力学.北京：国防工业出版社，2003.74～78

[2]蔡德咏，马大为等. 多管火箭炮两种定向管的比较分析.计算机仿真，2011年第3期endprint