基于人体纵截面特征曲线的体型分类
夏凤勤, 毋 戈, 谢昊洋, 钟跃崎,2
(1. 东华大学 纺织学院, 上海 201620; 2. 东华大学 纺织面料技术教育部重点实验室, 上海 201620)
基于人体纵截面特征曲线的体型分类
夏凤勤1, 毋 戈1, 谢昊洋1, 钟跃崎1,2
(1. 东华大学 纺织学院, 上海 201620; 2. 东华大学 纺织面料技术教育部重点实验室, 上海 201620)
针对人体体型分类标准选择问题,提出了通过人体纵截面特征曲线进行分类的方法。选择了124名青年女性,使用三维扫描仪扫描获得三维人体数据。并提取人体纵截面轮廓曲线数据,通过椭圆傅里叶拟合对原始曲线进行降噪处理。使用转向角函数将截面轮廓曲线转换成角函数曲线,并根据角函数曲线特征提取了5个特征指标,利用主成分分析法提取3个主成分。采用K-means聚类算法进行体型聚类,用伪F统计量确定最佳分类数目,将体型分为4类。最后通过对比分析4类体型特点,描述了各类体型在背部、背中心线、腹部、臀部和侧面厚度的差异。
纵截面曲线; 转向角函数; 主成分分析法; K-means聚类分析; 体型分类
由于人体体型的差异,同一套服装往往体现出不同的着装效果,对人体体型研究分类是服装号型划分的基础。目前,现有体型分类标准[1-2]大多是依据人体各维度的差值,其中我国依据胸腰差划分,ISO依据胸臀差划分,这对于胸围、腰围的横向体型特征区分较为有效,但缺乏对纵截面体型特征的区分。人体纵截面包含一些人体正面和背面无法获得的信息如:挺胸、驼背、凸腹、丰臀等,而这些信息与服装结构联系紧密,能为服装结构设计中腹省道的位置和大小提供依据。
快速发展的三维扫描仪可以短时间内获取人体体表的点云数据,而利用计算机图像技术又可精确计算并高效处理人体图像和形状分析,因此,国际上学者普遍采用三维扫描技术进行体型测量研究[3]。其中,服装工业发达的国家基于服装穿着效果与人体的关系对各国人体体型进行了大量的研究[4]。Connell等[5]将形状分析理论应用到人体体型与服装领域,提出了不能认为穿着同样大小服装的人体具有相同的体型,而不同体型穿着同样的服装可能有类似的形状;Simmons等[6]通过身体胸围、臀围、腰围、腹围、上腹围的体型特征数值把体型分为沙漏型、椭圆型、三角型、倒三角型、矩形、菱型、匙型、正沙漏型、倒沙漏型9种;Chung等[7]采用二阶段聚类分析方法通过年龄、性别和服装号型将6~18岁的中小学生分为9种类型。
目前,上述人体体型分类的研究均是基于人体横截面或横向特征曲线进行的,而关于人体纵截面特征曲线的研究很少,因此,本文利用三维扫描仪获取大量人体点云数据,并提取纵截面轮廓曲线数据,通过研究人体纵截面曲线特征,进行人体体型分类,为服装结构设计提供重要参考依据。
1 实验部分
1.1 数据采集
实验设备是本团队自行设计的多机扫描仪,采用12个RGB-Depth深度相机作为扫描单元。该套扫描系统扫描一个完整人体只用10~12 s时间。
实验对象为华东地区124名年轻女性,年龄为18~25岁,不区分高矮胖瘦。在无风、静音、室温(23~25 ℃)条件下,实验对象身着紧身内衣,采用标准测量姿势[8],利用多机扫描仪装置获取人体扫描样本数据。然后对人体扫描样本数据进行降噪、简化等处理,并以OBJ格式导出。为保证实验样本的随机性,从124个人体扫描样本中随机抽取60个样本作为研究对象。
人体纵截面特征曲线主要研究对象为人体躯干部分,不包括头部和四肢,将扫描人体样本数据导入Geomagic Studio逆向软件,在系统坐标系中将人体的主要方位与坐标轴对齐。其中,以XOZ面为水平面,人体的上下(高度)方向和Y轴对齐,向上为正方向;左右(宽度)方向和X轴对齐,向左为正方向;前后(厚度)方向与Z轴对齐,前为正方向。然后利用Geomagic Studio选取扫描人体的躯干部分,并提取过人体中心线的纵截面轮廓线,即人体纵截面特征曲线,如图1所示。

图1 人体切割位置与纵截面轮廓线Fig.1 Cutting position and longitudinal section cure of human. (a)Human body cutting; (b)Face of body; (c)Back of body; (d) Longitudinal section cure
1.2 数据预处理
由于扫描噪声的存在,人体截面轮廓曲线可能会包含异常尖刺、孔洞等形态。为便于分析,需要对原始截面轮廓曲线进行降噪处理。即对于人体纵截面曲线,可采用椭圆傅里叶级数逐步逼近的方式来描述[9]。把人体纵截面的封闭平面曲线看作动点沿周长的运动轨迹,利用椭圆傅里叶级数表示曲线上点坐标沿坐标轴的投影,然后将曲线离散为若干采样点近似描述,则由坐标轴方向的椭圆系数构成曲线的椭圆傅里叶描述。谐波次数越大,椭圆系数越多,描述的曲线越接近原始形态。
当采用不同的谐波次数N对人体纵截面轮廓曲线进行拟合时,发现当N小于5时,拟合曲线过于光滑,难以体现原始曲线的特征;当N大于20时,又起不到去除噪声的作用。N为20时曲线带有明显棱角,不圆滑。经过多次试验对比分析发现当N为15时原始曲线上带有明显棱角和波动的部分已经被柔化成了平滑圆润的曲线,可以很好的反映曲线特征,并且达到了良好的降噪效果,如图2所示。因此,后续处理中皆取N=15对人体纵截面曲线进行拟合。

图2 不同最大谐波次数N下的纵截面拟合效果Fig.2 Fitting effect of longitudinal section cure with different maximum harmonic numbers.(a)N=5;(b)N=15;(c)N=15 and N=20
在完成纵截面轮廓曲线的拟合之后,需要对其形态特征进行分析,以便后续分类识别。本文采用转向角函数对其形态进行表征。
2 方 法
2.1 转向角函数算法转化
转向角函数[10-11]是将平面图形用直角坐标系图像表示,能够更形象地体现各图形间的差异性。为便于对比分析各人体纵截面轮廓曲线间的差异性,采用转向角函数算法将纵截面曲线转化为直角坐标系函数图像。具体做法是:选取截面曲线最低点为起始点P1,横轴为点P1开始沿着曲线到下一个相邻点的距离,纵轴为各点沿着曲线的转向角的叠加。转向角函数θ(S)为:
式中:n为点的个数;转向角θi为点(Xi,Yi)与点(Xi+1,Yi+1)的连线与X轴的逆时针夹角(i=1,2,…,n);s为pi与中心点的连线和P1与中心点连线的夹角;li为累积长度。用这种方法将截面形状的长度和转向角反映到直角坐标系中来代替原始信息[12-13],结果如图3所示。

图3 截面曲线和转向角函数曲线Fig.3 Longitudinal section curve and corresponding turning function curve.(a)Longitudinal section curve;(b)Corresponding turning function cure;(c)60 longitudinal section curves superposition;(d)60 corresponding turning function cures superposition
对比分析60个转向角函数曲线,曲线的变化趋势基本一致反映了样本人体轮廓的总体相似性,但曲线的波峰个数、前2个波峰间距、小结个数以及曲线的最大值和终值等不同,说明样本个体体型存在差异性。根据样本人体纵截面轮廓曲线的转向角函数曲线差异,提取波峰的个数X1、前2个波峰间的距离X2、小结个数X3、曲线最大值X4和曲线终点值X5这5个特征指标变量,以便进行人体体型分类。
2.2 主成分分析
为提高分类指标的针对性,利用SPSS软件对这5个特征指标变量进行主成分分析,根据主成分个数提取原则[15],提取特征值大于1的前3个主成分,其中第1、2、3主成分的特征根分别为2.038、1.280、1.031,共解释了总变异的86.977%,结果如图4所示。

图4 各主成分方差贡献率Fig.4 Explaining variances of principal components
为了检验3个主成分之间的相关性,进行因子协方差计算,结果如表1所示。各主成分之间的数据为0,说明3个主成分之间是不相关的,因此该主成分分析是有效的。为了得到各主成分与五个特征指标变量之间的关系,进行因子载荷分析,结果如表2所示。每个载荷量表示主成分与对应变量的相关系数,其绝对值越大表示相关性越大。由表2可知:波峰个数和最大值在第1主成分中占有较高的载荷,第1主成分反映了这2个指标的信息,用F1表示;第2主成分主要反映了峰间距,用F2表示;第3主成分主要反映了小结个数和终点值,用F3表示,其对应关系如下:
F1=-0.45X1-0.21X2-0.34X3+0.68X4+0.41X5
F2=0.46X1+0.67X2-0.42X3+0.05X4+0.40X5
F3=0.41X1-0.31X2+0.57X3+0.07X4+0.64X5
提取的3个主成分基本上反映了全部特征指标信息,因此,可以用3个主成分变量代替原来的5个特征指标变量。
2.3 K-means聚类分析进行体型分类
应用聚类分析中的K-means聚类[16]算法依次假设60个研究样本可以分为K(K=2、3、4…)类,并确定相应的K个初始聚类中心,然后按照最小距离原则将每个样本分配到某一类中,之后不断地迭代计算各类的聚类中心并以新的聚类中心调整聚类情况,直至迭代收敛。利用伪F统计[17-18]作为判别函数来确定K值,计算公式[19]如下:
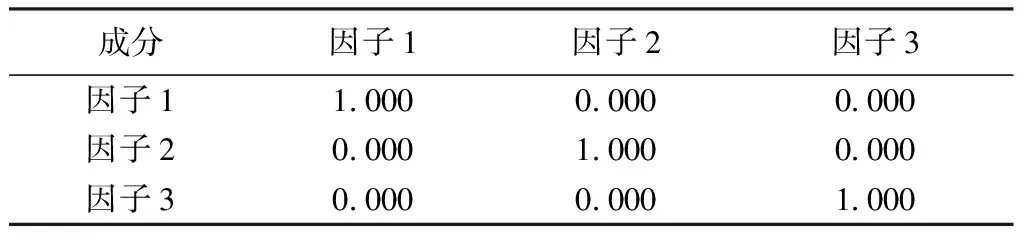
表1 因子协方差矩阵

表2 因子载荷矩阵
式中:T为样本数据的总离差平方和;PK为类内离差平方和;n是样本个数;K为聚类数目。
由上式可知,当聚类数目K固定时,如果聚类效果好,类间离差平方和比类内离差平方和大,则PPFS较大,当PPFS最大时聚类结果最佳。当K值增大时,PK减小,(T-PK)增大,PPFS先增大后减小。当PPFS达到最大值时,对应K值就是最佳聚类数目。根据公式(8)计算的PPFS值如图5所示,当聚类数目为4时,PPFS值最大,因此,确定最佳聚类数目为4类。

图5 PPFS与分类数目关系图Fig.5 Relationship between PPFS value and class number
当聚类数目为4时,经过22次迭代计算,最终聚类中心与初始聚类中心相比发生了很大变化,如表3所示。该聚类分析方差如表4所示,其中3个主成分得分系数中任意一个得分系数造成的类间均方都远大于类内均方,且3个主成分显著性都小于0.01,说明类间差异极显著,即3个主成分的得分聚类结果都比较清晰,分类明确。由于3个主成分描述了86.977%的信息,因此对体型的分类结果比用单一指标进行分类更科学。

表3 聚类中心

表4 方差分析表
将60个研究样本分为4类,每类中有依次24个、22个、9个、5个。将各类体型的数据从人体数据库中筛选出来,并选取各类典型人体纵截面轮廓曲线如图6所示,及其对应的人体模型躯干部分,如图7所示。对比分析4类人体体型的差异,分析结果如表5所示。
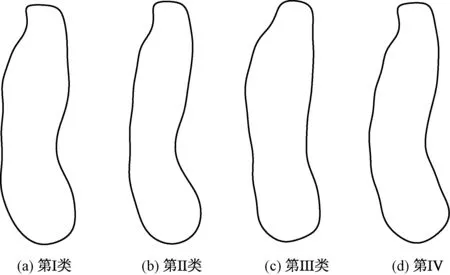
图6 第Ⅰ~Ⅳ类截面曲线Fig.6 Longitudinal section cure from class Ⅰ to class Ⅳ.(a)Class Ⅰ;(b)Class Ⅱ;(c)Class Ⅲ;(d)Class Ⅳ

图7 第Ⅰ~Ⅳ类截面曲线对应人体模型Fig.7 Human body from class Ⅰ to class Ⅳ.(a)Class Ⅰ;(b)Class Ⅱ;(c)Class Ⅲ;(d)Class Ⅳ

类别背部背中心线腹部臀部侧面厚度I平坦凹陷平坦后翘薄II弯曲较凹陷微凸起较后翘较薄III较平坦无凹陷较平坦较平较厚IV较弯曲凹陷凸起下垂厚
3 结 论
1)采用椭圆傅里叶拟合人体纵截面轮廓曲线,当谐波次数为15时,既能很好的反映曲线特征,又能达到良好的降噪效果。
2)利用转向角函数将人体纵截面轮廓曲线转化为函数曲线,并选取5个特征指标,通过主成分分析,提取3个主成分变量。
3)针对3个主成分变量,利用K-means聚类算法将60个研究样本分为4类,分析总结了各类特点,完善了人体体型分类研究,为服装结构设计提供参考依据。
FZXB
[ 1] 白莉红, 张文斌. 女装号型标准中体型的划分方法[J]. 纺织学报, 2006, 27(7):113-116. BAI Lihong, ZHANG Wenbin. Classification methods of figure type in the female garment size standards[J]. Journal of Textile Research, 2006, 27(7):113-116.
[ 2] GOLDSBERRY E, SHIM S, REICH N. Women 55 years and older: part Ⅰ Current body measurements as contrasted to the PS 42-70 Data[J]. Clothing & Textiles Research Journal, 1996,14(2):108-120.
[ 3] LU Junming, WANG M J J. Automated anthropometric data collection using 3D whole body scanners[J]. Expert Systems with Applications, 2008, 35(1/2):407-414.
[ 4] OKABE K, YAMANA N, YAMAMOTO K. Figure evaluation of the adult females silhouette and relation between the figure and the dress silhouette[J]. Journal of the Japan Research Association for Textile End-uses, 1995, 36:45-50.
[ 5] CONNELL L J, ULRICH P V, BRANNON E L, et al. Body shape assessment scale: instrument development for analyzing female figures[J]. Clothing & Textiles Research Journal, 2006, 24(2):80-95.
[ 6] SIMMONS K, ISTOOK C L. Female figure identification technique (FFIT) for apparel: part Ⅱ: development of shape sorting software[J]. Journal of Textile & Apparel Technology & Management, 2004, 4(1):1-13.
[ 7] CHUNG M J, LIN H F, WANG M J J. The development of sizing systems for Taiwanese elementary- and high-school students[J]. International Journal of Industrial Ergonomics, 2007, 37(8):707-716.
[ 8] MORI G, MALIK J. Recovering 3D human body configurations using shape contexts[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(7):1052-62.
[ 9] 夏明, 陈益松, 张文斌. 基于椭圆傅里叶的人体胸围断面形状研究[J]. 纺织学报, 2014, 35(7):107-112. XIA Ming, CHEN Yisong, ZHANG Wenbin. Shape analysis of bust slice using elliptic Fourier[J]. Journal of Textile Research, 2014, 35(7):107-112.
[10] 章思亮, 臧德彦. 基于转向角函数的形状匹配算法[J]. 科技广场, 2009(1):118-121. ZHANG Siliang, ZANG Deyan. Shape matching algorithm based on the turning angle function[J]. Science mosaic, 2009(1):118-121.
[11] LIU Hongshen, QIN Feng. Method of determining the function of description of shape in shape matching[J]. Journal of Huazhong University of Science and Techno-logy (Nature Science Edition), 2005, 33(4):13-16.
[12] ARKIN E M, CHEW L P, HUTTENLOCHER D P, et al. An efficiently computable metric for comparing polygonal shapes[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1991, 13(3):209-216.
[13] RODRIGO A S, GOONETILLEKE R S, WITANA C P. Model based foot shape classification using 2D foot outlines[J]. Computer-Aided Design, 2012, 44(1):48-55
[14] DUBOIS S R, GLANZ F H. Correction to an autoregressive model approach to two-dimensional shape classification[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1986, 8(1):55-66.
[15] 张文霖. 主成分分析在SPSS中的操作应用[J]. 市场研究, 2005(12):31-34. ZHANG Wenlin. Application of principal component analysis in SPSS[J]. Marketing Research, 2005(12): 31-34.
[16] 方方, 王子英. K-means聚类分析在人体体型分类中的应用[J]. 东华大学学报(自然科学版), 2014, 40(5):593-598. FANG Fang, WANG Ziying. Application of K-means clustering analysis in the body shape classification[J]. Journal of Donghua University(Natural Science Edition), 2014, 40(5):593-598.
[17] 骆嘉伟, 李仁发, 张白妮. 基于多维伪F统计量的基因表达动态聚类分析方法研究[J]. 系统仿真学报, 2006, 18(3):586-589. LUO Jiawei, LI Renfa, ZHANG Baini. Study on dynamic clustering analysis method for gene expression data based on multidimension pseudo F-statistics[J]. Journal of System Simulation, 2006, 18(3):586-589.
[18] VOGEL M A, WONG A K C. PFS clustering me-thod[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1979, 1(3):237-45.
[19] BEZDEK J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York: Plenum Press, 1981:43-48.
Classification of body shape based on longitudinal section curve
XIA Fengqin1, WU Ge1, XIE Haoyang1, ZHONG Yueqi1,2
(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.KeyLaboratoryofTextileScienceandTechnology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)
A classification method of the human body based on the longitudinal section cure was proposed for classification basis of somatotype. A 3-D human body measurement instrument was used to measure 124 young female samples. The point cloud data of the longitudinal section cure could be got, and analyzed and processed by some way. The elliptical Fourier fitting was used for original curve denoise processing. To get turning function cure of longitudinal section curve a function which was called turning function was used, then five characteristic indexes were extracted according to characteristics of turning function cure. A method called the principal component analysis was used to extract three principal components. As for shape clustering the K-means cluster analysis was used, and the Pseudo F-statistics was used to determine the optimal class number. Then longitudinal section curve could be divided into four classes. Finally, the difference on back, centre back seam line, abdomen, hip and side thickness of all kinds of shapes was described.
longitudinal section curve; turning function; principal component analysis; K-means cluster analysis; somatotype
10.13475/j.fzxb.20160602006
2016-06-12
2016-11-13
国家自然科学基金项目(61572124);上海市自然科学基金资助项目(14ZR1401100)
夏凤勤(1991—),女,硕士生。研究方向为人体纵截面特征曲线的线型分类。钟跃崎,通信作者,E-mail:zhyq@ dhu.edu.cn。
TS 941.2
A

