一种新的航天器姿态快速测量方法
张 杰,张 巍,范生宏,王 顺,鲁利刚
(1. 北京卫星制造厂,北京 100080;2.北京控制工程研究所,北京 100190;3. 北京普达迪泰科技有限公司,北京 100083)
一种新的航天器姿态快速测量方法
张 杰1,张 巍2,范生宏3,王 顺3,鲁利刚1
(1. 北京卫星制造厂,北京 100080;2.北京控制工程研究所,北京 100190;3. 北京普达迪泰科技有限公司,北京 100083)
针对航天器组件装调及实验阶段,姿态准直测量过程需要频繁建站的问题,提出了一种航天器组件姿态快速测量方法。该方法采用调整装置,将卫星本体坐标系XOY面调整到与大地水平,根据整星立方镜和组件立方镜的标定数据,快速反算出用于组件准直测量的经纬仪的理论指向,指导产品组件姿态的快速调整。经实验验证,该快速调整方法精度满足设计要求,测量效率大幅提升。
航天器姿态;准直测量;快速调整
0 引言
为了保证航天器的正常飞行和工作,地面总装阶段必须将航天器组件(星敏、天线、推进及控制装置等)调整到必要的几何精度[1]。由于产品结构复杂、尺寸较小或被测要素不易复现,较多情况下采用准直测量法予以解决[2]。即在该组件上安装立方镜(简称产品立方镜),通过经纬仪测量被测立方镜与基准立方镜之间的关系,来确定被测组件的位置和姿态[3]。
立方镜在航天器组件的位姿测量应用比较广泛[4],国内众多科研院所和高校都进行过相关的研究和实践,大都采用经纬仪工业测量系统建站和准直测量结合的方法[5-9],但该方法实际测量过程中需要多次互瞄建站,效率较低。提出了一种新的姿态快速测量方法,并验证了其精度和可行性。
1 传统方法
传统的测量方法一般使用经纬仪工业系统,通过多台经纬仪互瞄定向和尺度标定构建空间测量系统[7];对2组立方镜准直测量,分别计算立方镜坐标系与经纬仪坐标系间的关系;通过关系传递和数据计算,得到2组立方镜坐标系之间的关系,进而得到产品组件姿态参数。
应用该方法,至少需要使用4台经纬仪,保证每组立方镜的2个准直面可被观测。当组件实际姿态与理想状态偏离较大或组件经调整后对立方镜再次准直时,可能超出经纬仪准直测量范围,需要重新调整仪器,再次构建空间测量系统,然后重新测量、分析;至组件姿态偏离量在误差允许范围内时,终止建站操作。整个流程如图1所示。
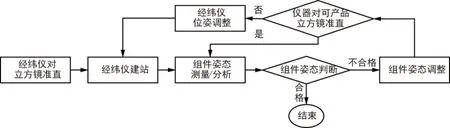
图1 传统方法测量流程图
2 改进方法
由于经纬仪准直量程有限,组件初始状态未知,产品姿态调整控制过程中,反复的系统建站操作,繁复的数据处理环节,导致方法实际应用效果不太理想。此处对传统方法提出改进。
如图2所示,卫星装配过程中,将卫星本体置放于支撑装置上,支撑装置的位姿可通过调整装置进行调节。
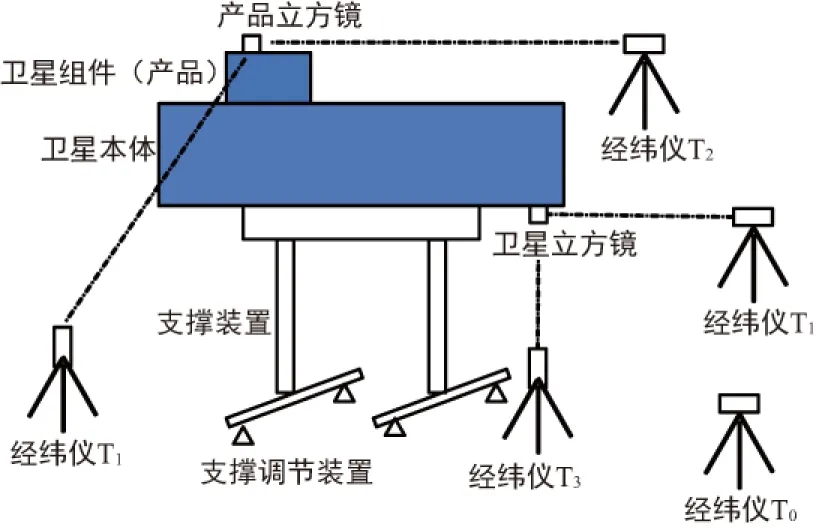
图2 产品立方镜准直示意图
经纬仪的仪器坐标系(也称为测站坐标系),建立方式定义如下:仪器调置呈水平状态,仪器三轴中心为原点,过原点沿铅垂向上为+Z轴,零度方位角视准方向为+X轴,由右手规则确定Y轴方向。仪器坐标系的XOY平面为水平面。假设卫星坐标系Z轴向上,XOY面与大地近似水平。则调整过程如下:
① 根据卫星坐标系和卫星立方镜坐标系的标定数据,计算出卫星坐标系XOY面与大地水平时,准直卫星立方镜的经纬仪T3、T4的水平角和天顶距;
② 根据步骤①计算出的理论水平角和天顶距,经纬仪对卫星立方镜姿态进行实时观测,指导调整装置使整星XOY面与大地严格水平,调整水平后,将准直整星X轴的水平角传递给T0,并将经纬仪T0水平度盘零方向置为与X轴平行;
③ 根据设计参数、标定数据等,计算得到产品立方镜与卫星坐标系的关系,即在卫星坐标系下,准直产品立方镜的经纬仪T1、T2的水平角和天顶距;
④ 将经纬仪搬到准直产品组件立方镜的位置T1和T2,根据步骤③计算出的理论值调整产品姿态,对产品立方镜准直图像予以实时观测、判读,对调整操作予以即时指导;
⑤ 产品姿态逼近理论值后,根据观测仪器参数值,计算得到产品立方镜和卫星坐标系的关系,进而得到在卫星坐标系下产品的最终姿态。
2.1 准直卫星立方镜的经纬仪角度计算
设卫星坐标系系O-XYZ先平移(xo,yo,zo),再旋转 (εx,εy,εz),最后缩放k倍后,转换到卫星立方镜坐标O′-X′Y′Z′。点P在O-XYZ中的坐标为(x,y,z),在O′-X′Y′Z′中的坐标为(x′,y′,z′),则卫星坐标系与卫星立方镜坐标系间的关系如下所示[10]:
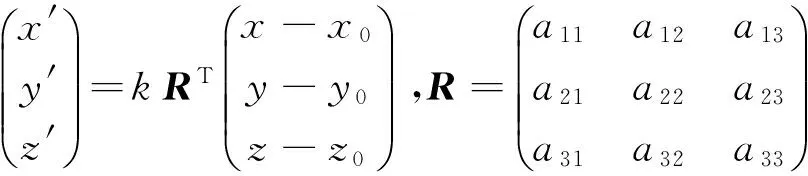
(1)
经纬仪T3准直立方镜坐标系的X轴,T4准直立方镜坐标系的Y轴,则卫星坐标系XOY面与大地水平时,经纬仪T3、T4准直卫星立方镜工作面时的角度H3、V3和H4、V4分别为:
(2)
2.2 指导调整卫星坐标系XOY面与大地水平
如图3所示,观测经纬仪目镜视场中准直图像,通过仪器瞄准十字线与准直图像水平线的位置关系,即可以准确判断出卫星立方镜工作面法线相对理论状态的偏离方向,并计算出偏离量;调整经纬仪角度调节钮,使两线重合,即可由仪器表盘读数准确得到立方镜工作面的法向偏差。如仪器目镜视场中不出现准直图像,说明在该方向上,卫星坐标系XOY平面与水平面夹角过大,超出经纬仪准直量程。可以先对卫星立方镜准直,通过准直状态下仪器俯仰角与90°的差值,判断出卫星立方镜工作面法向偏离方向及大小,对支撑调节装置进行初步调整,直到偏离量逼近允许误差区间(-k,k)。其中可能需要对经纬仪进行数次位姿调整,确保可对卫星立方镜实现准直。
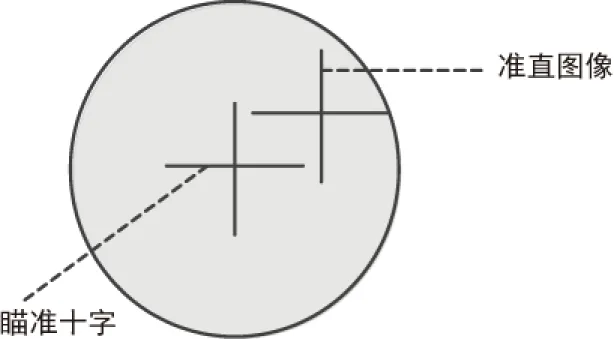
图3 经纬仪准直示意图
经纬仪T3、T4俯仰角调整至理论值,实时监测准直图像,根据支撑调节装置调节点和卫星立方镜工作面法向的空间位置关系,逐步调整各调节点高度。经过精确调整,可将卫星立方镜单个方向的法向偏差值控制在0.001°以内。
2.3 卫星坐标系X轴方位传递
经纬仪T3、T4空间互瞄,尺度标定,构建空间测站,建立测量坐标系T-XYZ;对卫星立方镜准直测量,得到卫星立方镜坐标系C-XYZ与T-XYZ的关系;根据卫星立方镜C-XYZ与卫星坐标系S-XYZ的关系,可得到卫星坐标系与测量坐标系T-XYZ的关系。由此,可计算出卫星坐标系X轴与测量坐标系的空间位置关系,得到其与经纬仪T3(或T4)仪器坐标系X轴的空间夹角β。
经过上步调整,卫星坐标系XOY平面与经纬仪T3(或T4)仪器坐标系XOY平面呈平行状态,将经纬仪T3(或T4)方位角调置呈β(或360°-β),即可使仪器视准方向与卫星坐标系X轴方向重合;将仪器该视准方向设为零度方位角,传递于经纬仪T0,则仪器坐标系T0-XYZ与卫星坐标系S-XYZ方向完全一致。
因卫星上需要调整的组件数量多,装调过程中始终保持经纬仪T0位置,将其作为基准仪器,传递基准角度。
2.4 准直产品立方镜的经纬仪水平角和天顶距计算
根据产品坐标系与卫星坐标系之间理论关系、产品立方镜与产品坐标系标定关系,可计算得到产品立方镜相对卫星坐标系的关系。计算过程如下:
产品坐标系下的坐标表示为(X,Y,Z),产品立方镜坐标系下的坐标为(X′,Y′,Z′),卫星坐标系下的坐标为(X″,Y″,Z″)。以产品坐标系为当前坐标系,其参数表示为(0,0,0,0,0,0,1),产品立方镜坐标系的坐标参数为(X01,Y01,Z01,εx01,εy01,εz01,k01),卫星坐标系的坐标系参数表示为(X02,Y02,Z02,εx02,εy02,εz02,k02),则产品立方镜坐标系在卫星坐标系下的坐标系的平移量和旋转矩阵推导如下[11-12]:
(3)
令M=R2-1″,则可由式(3)推导得出用于准直的经纬仪水平角和天顶距值。
2.5 产品姿态测量与调整
如图2对现场进行布局,保持经纬仪T0初始位置。经纬仪T1、T2对产品立方镜两相邻工作面进行准直,其中经纬仪T1瞄准立方镜+X方向,经纬仪T2瞄准立方镜+Y方向;经纬仪T0将零度方位角传递于经纬仪T1、T2。则经纬仪T1、T2仪器坐标系与卫星坐标系S-XYZ方向完全一致。
对产品立方镜精确准直测量,由2台仪器得到4个参数:经纬仪T1俯仰角V1、方位角H1及经纬仪T2俯仰角V2、方位角H2。
因而,在产品调整阶段,可根据经纬仪读数对产品姿态予以快速判断:① 当其中一项参数偏差超过最大允许误差k时,可判定产品姿态超差;② 当所有参数偏差均小于最大允许误差k的0.5倍时,可判定产品姿态合格。
当产品严重偏离理想状态时,与卫星坐标系调置水平状态相同,根据经纬仪T1、T2仪器读数指导初调过程,直至2个方向的3个姿态参数偏差均位于经纬仪准直量程内,其中涉及对经纬仪T1、T2的多次位姿调整。
2.6 姿态参数计算
在判定产品姿态合格后,需根据仪器读数,精确计算产品的实际状态,即确定产品立方镜坐标系和卫星坐标系的关系。
经对产品立方镜严格准直后,经纬仪T1俯仰角V1、方位角H1,经纬仪T2俯仰角V2、方位角H2。由于T1测站准直向量的反方向为与卫星坐标系+X轴平行的向量,T2测站准直向量的反方向为与卫星坐标系+Y轴平行的向量。设2个坐标系的转换矩阵如下:

(4)
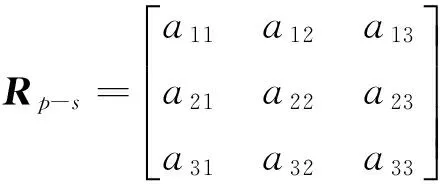
(5)
则观测角度与坐标系旋转矩阵间的关系如下:

(6)
a11、a21、a31即为产品立方镜X轴在卫星坐标系下的向量,a12、a22、a32为产品立方镜Y轴在卫星坐标系下的向量,X轴与Y轴叉乘可得到产品坐标系Z轴在卫星坐标系下的向量,即旋转矩阵的a13、a23、a33。根据准直解算出产品立方镜和卫星坐标系的实际关系,对比根据设计和标定数据计算出的产品立方镜参数,即可解获得产品的实际状态。
3 实验验证
为了验证该方法的可行性,采用传统方法先进行准直测量,再采用快速测量方法进行3组准直测试,实验结果如表1所示。
表1 标定实验数据/(°)
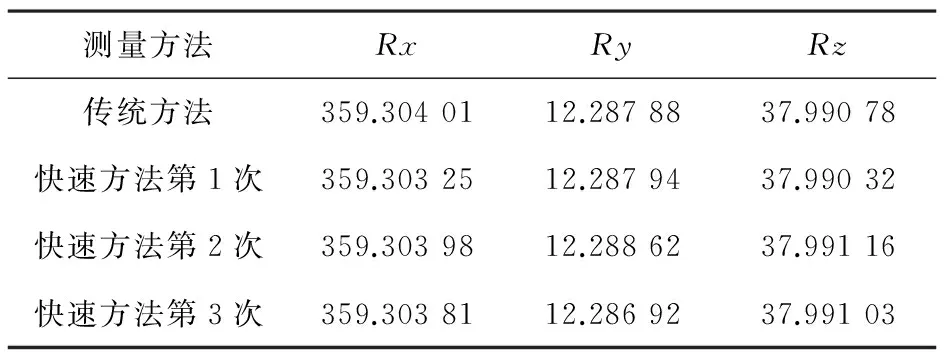
测量方法RxRyRz传统方法359.3040112.2878837.99078快速方法第1次359.3032512.2879437.99032快速方法第2次359.3039812.2886237.99116快速方法第3次359.3038112.2869237.99103
从表1测试结果可以看出,3组快速测量实验自身重复性较好,其测试结果与传统方法标定结果各轴的差均小于3 s,可以满足大部分航天器组件的总装精测要求。
4 结束语
本文对航天器准直测量的传统方法进行了介绍,针对传统方法存在的问题,提出了航天器姿态测量的快速测量方法,对方法的原理、使用范围和实际效果进行了详细介绍。相对于传统的测量流程,该方法实现了对组件姿态的快速测量和调整,简化了经纬仪搬站和定向过程,极大地提高准直测量的效率和简易型,应用前景广阔。
[1] 徐福祥.卫星工程概论[M].北京:中国宇航出版社,2004.
[2] 张杰,王京海,石磊,等. 一种经纬仪自准直姿态实时测量方法[J]. 光电工程,2015,42(5):39-44.
[3] 杨再华. 航天器总装精度测量方法分析[J]. 航天器环境工程,2007,24(6):390-392.
[4] 柏宏武,冀有志. 立方镜在航天器天线总装测量中的应用[J]. 空间电子技术,2013,10(2):62-66,82.
[5] 杨振,李广云,黄桂平,等. 基于自准直的立方镜姿态测量方法研究[J]. 宇航计测技术,2010,30(2):14-17.
[6] 黄桂平,叶声华,李广云,等. 经纬仪非接触大尺寸三坐标测量系统的开发及其在航天器检测中的应用[J]. 上海计量测试,2002,29(3):9-12.
[7] 邓勇,李宗春,范百兴,等. MetroIn在飞船精度测量中的应用[J]. 导弹与航天运载技术,2009(4):47-51.
[8] 杨振,李广云,范百兴,等. 多种互瞄条件下立方镜准直传递方法研究[J]. 宇航计测技术,2013(6):10-12.
[9] 沈兆欣,陈晓晖. 电子经纬仪测量系统中立方镜坐标系建立技术探讨[J]. 宇航计测技术,2006,26(4):73-75.
[10]黄桂平. 数字近景工业摄影测量关键技术研究与应用[D].天津:天津大学,2005.
[11]魏新国,张广军,樊巧云,等. 太阳敏感器测量坐标系与立方镜坐标系转换矩阵的标定[J]. 光学精密工程,2009,17(4):849-853.
[12]王智,吴国栋. 测绘相机立方镜与星敏立方镜转换矩阵的标定[J]. 光学精密工程,2012,20(1):96-101.
A New Method for Rapid Measurement of Spacecraft Attitude
ZHANG Jie1,ZHANG Wei2,FAN Sheng-hong3,WANG Shun3,LU Li-gang1
(1. Beijing Spacecrafts,Beijing 100194,China;2. Beijing Institute of Control Engineering,Beijing 100190,China;3. Beijing Prodetec Technology Co.,Ltd,Beijing 100083,China)
Aiming at the problem of frequent alignment in the process of spacecraft alignment and experiment,a new method is proposed to measure the attitude of spacecraft components. This method uses the adjusting device to adjust the XOY surface of satellite coordinate system parallel with the Geodetic plane,then according to the calibration data of entire satellite cubic mirror and component cubic mirror,calculates the theodolite angle quickly,and guide the rapid adjustment of product component attitude. The experimental results show that the precision of this method can meet the design requirements,and the measurement efficiency is significantly improved.
spacecraft attitude;alignment measurement;rapid adjustment
10. 3969/j.issn. 1003-3114. 2017.04.16
张杰,张巍,范生宏,等. 一种新的航天器姿态快速测量方法[J].无线电通信技术,2017,43(4):67-70.
[ZHANG Jie,ZHANG Wei,FAN Shenghong,et al. A New Method for Rapid Measurement of Spacecraft Attitude[J].Radio Communications Technology,2017,43(4):67-70. ]
2017-04-20
国防科研基础计划项目
张 杰( 1979—) ,男,高级工程师,主要研究方向:精密测量技术。范生宏(1978—),男,博士,主要研究方向:数字近景摄影测量与精密工程测量技术。
文献标志码:A 文章编号:1003-3114(2017) 04-67-4

