基于零相位与光流法的混合超声弹性成像算法的研究

李元瑞，张勇德

中国医科大学 生物医学工程系，辽宁沈阳 110000

基于零相位与光流法的混合超声弹性成像算法的研究

李元瑞，张勇德

中国医科大学 生物医学工程系，辽宁沈阳 110000

鉴于超声弹性成像传统的时域互相关算法在估计组织位移时效率低下这一问题，本文提出了一种基于零相位与光流法的混合超声弹性成像方法。首先利用零相位法来获得组织压缩前后的位移场，将结果作为光流法的初始位移；然后采用经典光流法对为位移场进行矫正，抑制由于组织横向形变所带来的去相关；最后采用最小二乘法对位移场进行计算获得了组织的轴向应变。本文利用仿真数据对算法进行了验证，并且定性分析了不同压缩量下的算法的性能。实验结果表明，本论文中提出的零相位和光流法的混合超声弹性成像算法所得纵向位移图和纵向应变图与有限元结果基本一致，证明了算法的正确性。

超声弹性成像；光流法；零相位迭代；去相关；最小二乘法

引言

病理变化一般都伴随着组织硬度的变化，组织硬度变化可以从另一个角度反映肿瘤的活性。乳腺导管癌约比正常皮下脂肪组织硬23 dB，浸润性癌症有28 dB；在前列腺癌方面，癌症组织硬度比正常组织高10 dB以上。目前临床上大部分医学影像设备主要是对体内组织结构进行成像，有时候医生只依靠反映组织结构信息的图像，是无法做出最终的诊断的。检查组织软硬程度的传统方式为手工触诊，然而手工触诊一般仅限于身体浅表处病灶的检测，而位于身体深部的肿块几乎不能通过手工触诊来检测，而且检测结果在很大程度上依赖于医师的主观判断。超声弹性成像这一概念最早是由Ophir等[1-2]于1991提出的，通过外部或内部激励使组织产生微小形变，计算压缩前后回波信号互相关系数，得到位移分布，通过计算位移梯度得到局部组织应变。目前，根据所施加压缩形变的激励方式不同，可以将超声弹性成像分为静态弹性成像和动态弹性成像[3-4]，准静态超声弹性成像技术由于实现简单，不需要额外的辅助设备，而且易于实时成像，因此一直以来是弹性成像领域的研究热点。目前，超声弹性成像技术在国内还仍处于理论研究阶段，研究水平和国外还有很大的差距，其原因主要在于国内的许多研发单位无法获得进行弹性评估所需的射频回波数据。因此提高我国超声弹性成像技术的研发水平，在临床上普及具备该功能的超声诊断设备，探索和扩大其应用范围，对于提高我国医疗水平具有十分重要的意义。

1 材料与方法

1.1 一般资料

在超声弹性成像算法研究中，可供研究的数据一般有3种来源：① 通过仿真软件得到射频仿真数据；② 仿体数据，通过制作得到的仿体，利用超声射频回波信号采集系统获取；③ 在体数据，从实际的病患某些器官组织获得数据。仿真数据由于组织结构简单，而且包裹物和嵌入物弹性模量可以根据需求设置，适合用于评价算法性能。本次实验为了得到仿真数据，设计开发了用于超声弹性成像的射频回波信号仿真系统。利用Matlab建立了组织仿体模型，产生散射点，并利用Comsol软件对相应的组织模型进行有限元分析，得到相应压缩量下组织的应变和位移分布，从而计算出仿体模型在被压缩后各散射点的位置分布[5-9]，流程图，见图1。

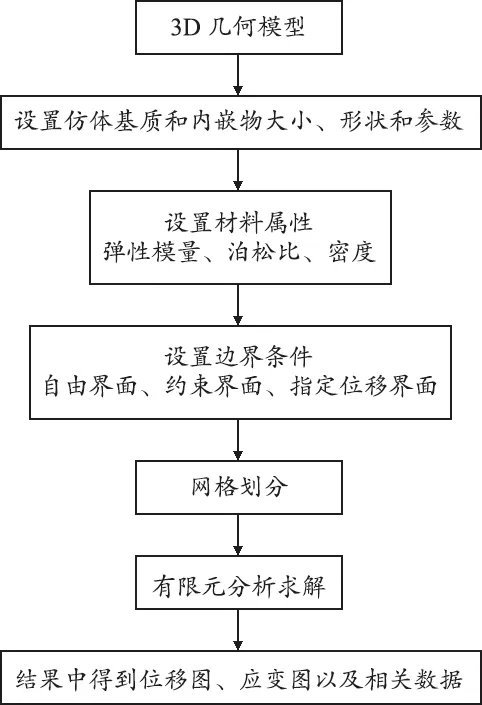
图1 仿真流程图

有限元分析方法应用在生物力学中，可以模拟出复杂的生物组织并对各部分结构有更加深入的研究，本文就是利用有限元方法来模拟人体中有肿瘤或者囊肿的病变部位。通过有限元分析和求解，将经过网格划分后的仿体模型进行有限元分析求解，得到相应的仿真结果。图2给出了1%压缩量下，一个嵌入物仿体模型的仿真位移图和轴向应变图，并以伪彩色显示。图2a、2b分别是三维位移图和应变图。

1.2 实验方法

本文利用计算机仿真的射频回波信号对混合算法的性能进行了定性分析，算法实现的硬件平台为Dell T5600图形工作站，6核CPU，主频2.0 GHz，内存4 GB，编程语言为Matlab R2014a。算法主要参数设置如下：零相位法窗长129，窗间间隔16，迭代次数5次，光流法平滑项因子α=640。

图2 仿体模型

初始位移场的获得，利用Field-II获得的压缩前后的射频回波数据，将每一条扫描线压缩前的射频数据按每隔16个数据点设置为一个窗口，压缩后的射频数据的轴向窗口长度要大于压缩前的窗口，并且加上上一次迭代得到的位移偏移量，每隔一个窗口计算一次压缩前射频数据与压缩后的射频数据的复数互相关，在零相位时得到压缩前后射频数据的位移。

零相位迭代算法其中一条扫描线的某一窗口的位移求解示意图（图3）。迭代次数少得到的零相位对应下的位移不精确，迭代次数太多影响计算效率，在本文介绍的零相位迭代算法中设置迭代次数为50[10-11]。从图中可以看出，虽然相位逐渐逼近零相位但是并没有达到零相位，但位移与相位已呈现出线性关系，本文基于这一点提出了对相位与位移进行线性拟合，减少迭代次数，进行5次迭代并保存每次迭代所得到的压缩前后射频数据的位移与相位。设相位为y，位移为x，对5次迭代的结果进行直线拟合y=kx+b求得斜率与截距，在零相位时可以求得压缩前后射频数据的位移x=-b/k，较之于之前的50次迭代次数可以得到较好的位移结果并且节省了几倍的时间。

零相位迭代算法即没有做任何噪声处理并且没有考虑组织位移的连续性，因而得到的位移场噪声比较明显，光流法本身有平滑机制，所以本文采用直接利用零相位迭代算法得到的位移作为光流法的初始值[12]。

应变是对得到的位移场进行数值差分进行的，这种梯度运算对位移估计噪声有放大的作用，最小二乘应变估计实现的目标是控制噪声进一步放大，在实现上采用分段线性曲线拟合所估计得到的位移场[13-14]。

图3 位移-相移图

2 结果

2.1 仿真数据结果分析

组织受压后，压缩后的射频数据中每个点的位移都会发生一定程度的变化，通过Matlab画出129条扫描线中的第60条扫描线的位移图（图4）。图4a中纵坐标是位移量，横坐标为射频数据的点数。截取射频数据6500个点，在1/100压缩量的仿真数据中，可能存在的最大位移是-60，组织受压后，各个点都有相应的位移变化，由于仿真数据中中间区域是球形囊肿，弹性模量一致所以在扫描线中的中间区域表现为位移基本一致；而图4b中，采用零相位与光流法的混合算法抗噪能力强，得到的单条扫描线的位移图没有毛刺，位移随组织深度增加而加大，同时外基质在外力作用下位移变化较快，而嵌入物部分位移变化缓慢，由此可以验证实验结果与理论分析一致，证明了算法的有效性。由图4a可以看出，经典的零相位法由于没有位移连续性的约束，结果容易受到信号去相关因素的影响，缺乏抗噪能力，因此位移曲线存在着大量的噪声；而本文提出的算法获得的位移曲线非常平滑，如图4b所示，具有很好的抗噪声能力。图4c～d为1%压缩量下，零相位迭代算法与本文算法得到的纵向位移图，图中蓝色代表位移较大，红色代表位移小[15-17]。图4c中虽然噪声明显但依然可以清晰的看到在图形中间与仿体中间嵌入物的区域，零相位迭代算法依赖于算法中上一次计算的结果，因为最开始的初始位移并没有引入先验值，而迭代算法每经过一次迭代又会放大一次错误，所以位移图中出现一些跳变。在零相位与光流法的混合算法中，首先通过零相位迭代算法得到位移场，代入光流法中进行计算得到最后的精确位移。

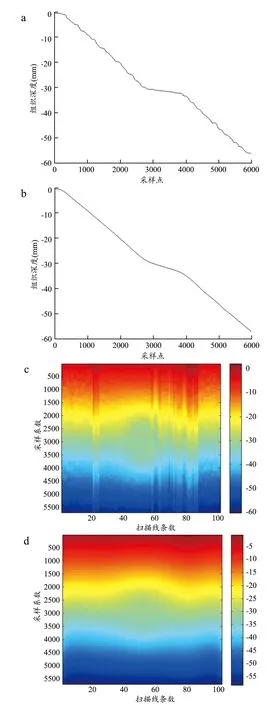
图4 129条扫描线中的第60条扫描线的位移图

2.2 最小二乘法应变图

本文是对离散位移场进行局部最小二乘拟合来计算应变场，针对1%、2%及4%等不同压缩量下获得的应变场与经典的零相位法进行了分析和比较。1%压缩量不同算法纵向应变图有限元仿真的应变图对比，见图5；2%压缩量的不同算法的纵向应变图对比，见图6；本文所采用的零相位与光流法结合的方法在2%压缩量的条件下，运算速度与去除应变图噪声的优势明显好于零相位迭代算法；4%压缩量不同算法的纵向应变图对比，见图7。从图7中可以看出4%压缩量的应变图，当应变较大时尤其在边缘处，检测结果较差，因为在大压缩量的情况下，边缘形变大，窗口的相位匹配不准确而且零相位迭代法的初值依赖于上次迭代的结果，导致位移估计错误得不到理想的应变图，但与零相位迭代算法相比，本文的混合算法有更高的精确度，这也是使用光流法对零相位迭代算法进行横向位移修正的优势所在。

图5 1%压缩量不同算法纵向应变图有限元仿真的应变图

2.3 仿真数据结果分析

从仿真结果与算法运行结果对比，嵌入物大小清晰可辨；周围基质处颜色区域分布大致相似，基本上验证了算法的可行性，以及对噪声的抑制功能。基于零相位与光流法的混合算法每次运行都可以得到相同的实验结果说明了具有可靠的实验重复性，在实际的临床应用中，实时显示是一个重要需求，所以对算法计算效率的提高，节约时间成本显得尤为重要。本实验中所采用的PC设备性能参数：① CPU，Inter（R）xeon（R）E5-26200；② 内存，RAM 4.00 GB。从算法的计算时长来看，所有程序代码在MATLAB中运行。1%压缩量，零相位迭代算法需要469.29 s，而本文中利用位移-相位信息进行拟合的算法只需要48.23 s，速度提升了近10倍。

图6 2%压缩量的不同算法的纵向应变图

图7 4%压缩量不同算法的纵向应变图

3 讨论

本文是对超声弹性成像算法的研究，改进方案能有效提高计算效率，在大幅度减少迭代次数的前提下，通过直线拟合节省运行时间。此外，零相位迭代算法没有考虑横向应变的影响，用零相位迭代算法得到的位移场作为光流法的位移初始值，得到了经过横向位移修正后的纵向位移。

生物组织发生病变通常伴随着组织硬度上的变化，即组织力学属性会发生变化。而检查组织硬度基本要靠触诊，超声成像技术可对组织硬度属性进行成像为临床疾病诊断提供更加丰富的功能信息，超声弹性成像的实时性对于其临床使用而言同样具有非常重要的意义，因而探索计算速度快成像效果好的准静态超声弹性成像有着广泛的临床应用价值。零相位法由于采用牛顿迭代法仅通过少量迭代便可获取组织位移，相比互相关算法具有较高的成像速度，然而该方法只考虑了组织的轴向运动，无法解决组织横向形变所带来的去相关问题。光流法通过求解偏微分方程可以获得组织的二维位移场，而且算法的效率很高。用光流法进行组织运动估计时，随着组织深度的增加，组织的位移逐渐加大，不准确的初始位移将导致巨大的计算误差甚至计算失败。本文主要对准静态情况下的超声弹性成像技术进行了深入的研究，在了解了超声弹性成像的基础知识之后。使用超声射频数据，实现了改进了计算效率的零相位迭代算法的位移估计，经过高斯滤波的平滑滤波后，并且结合光流法的优点，最后利用最小二乘法进行了组织的应变估计，得到与有限元仿真基本一致的结果。

本研究就现阶段而言还需进一步完成的工作有如下几个方面：① 零相位迭代算法在大压缩量下的应变估计，由于压缩量过大导致相位匹配不准，检测结果较差，需要找到解决的办法；② 本文算法得出的应变图嵌入物边界不光滑，对比度不好；③ 本文提出的零相位与光流法混合算法并没有计算射频数据的横向位移，在以后的工作中要进一步进行完善。

[1] Ophir J,Cespedes I,Ponnekanti H,et al.Elastography: a quantitative method for imaging the elasticity of biological tissues[J].Ultrason imaging,1991,13(2):111-134.

[2] Ophir J, Alam SK,Garra B,et al.Elastography: ultrasonic estimation and imaging of the elastic properties of tissues[J].P I Mech Eng H-J Mec,1999,213(3):203-233.

[3] Krouskop TA,Wheeler TM,Kallel F,et al.Elastic moduli of breast and prostate tissues under compression[J].Ultrason Imaging,1998,20:260-274.

[4] Pan X,Gao J,Tao S,et al.A two-step optical flow method for strain estimation in elastography: Simulation and phantom study[J].Ultrasonics,2014,54(4):990-996.

[5] Hasan MK,Anas EMA,Alam SK,et al.Direct mean strain estimation for elastography using nearest-neighbor weighted least-squares approach in the frequency domain[J].Ultrasound Med Biol,2012,38(10):1759-1777.

[6] Alam SK,Feleppa EJ,Kalisz A,et al.Prostate elastography: preliminary in vivo results[J].Int Soc Opt Photonics,2005: 339-345.

[7] Dickinson RJ,Hill CR.Measurement of soft tissue motion using correlation between A-scans[J].Ultrason Med Bio,1982, 8(3):263-271.

[8] 刘鑫.基于超声弹性成像技术的生物组织应变估计算法仿真研究[D].哈尔滨:哈尔滨工业大学,2012.

[9] 刘彦.人体组织的超声弹性成像方法研究[D].哈尔滨:哈尔滨工业大学,2011.

[10] 王勇萍.人体组织实时超声弹性成像技术研究[D].哈尔滨:哈尔滨工业大学,2012.

[11] 袁金伟.超声弹性成像中的位移和应变估计[D].浙江:浙江大学,2012.

[12] 李伟方.超声弹性成像全局位移场估计算法研究[D].武汉:武汉理工大学,2013.

[13] 张耀南,李宏亮,康雁.基于二维压缩扩展和光流法的组织应变估计方法[J].东北大学学报(自然科学版),2013,539(9):22-26.

[14] Barron JL,Fleet DJ,Beauchemin SS,et al.Performance of optical flow techniques[A].Computer Vision and Pattern Recognition[C].Newyork:IEEE,1992:236-242.

[15] 祝彦平.基于互相关的超声应变成像研究[D].沈阳:中国医科大学,2012.

[16] 龙琪.基于图形处理器的超声仿真平台[D].安徽:中国科技大学,2010.

[17] 孙瑞超,唐亚男,李灵,等.实时超声弹性成像原理与方法[J].中国医疗器械信息,2013,(6):1-9.

本文编辑 聂孝楠

Research on Hybrid Ultrasonic Elastography Algorithm Based on Zero Phase and Optical Flow

LI Yuan-rui, ZHANG Yong-de
Department of Biomedical Engineering, China Medical University, Shenyang Liaoning 110000, China

In view of the problem that the traditional time-domain cross-correlation algorithm of ultrasound elastography in estimating tissue displacement compute-intensive and inefficient, this paper proposed a hybrid method of ultrasound elastography based on phase zero estimation and optical flow method. Firstly, the zero phase was used to estimation method to obtain coarse displacement field, as a result of the initial displacement for optical flow; then the classical optical flow method Horn & Schunck (HS) optical flow method was used to correct for the displacement field; finally the least squares method was used to calculate the displacement field obtained axial strain organizations. In this paper, the simulation data algorithm was validated and the impact of simulation data under different compression on the experimental results was discussed. The experimental results showed that the longitudinal displacement diagram and the longitudinal strain map of the zero-phase and the optical flow method proposed in this paper were consistent with the finite element results, and the correctness of the algorithm was proved.

ultrasound elastography; optical flow; phase zero estimation; decorrelation; least squares method

R318.6

B

10.3969/j.issn.1674-1633.2017.06.016

1674-1633(2017)06-0061-05

2016-10-20

2016-12-20

省级科技项目“基于相关相位和光流法的二维实时超声弹性成像方法研究”（L2012294）。

张勇德，副教授，主要研究方向为超声弹性成像。

通讯作者邮箱：zyd1977@sina.com