基于改进K均值聚类的入侵检测算法研究

何明亮陈泽茂黄相静

（1.海军工程大学信息安全系武汉430033）（2.91681部队宁波315731）

基于改进K均值聚类的入侵检测算法研究

何明亮1陈泽茂1黄相静2

（1.海军工程大学信息安全系武汉430033）（2.91681部队宁波315731）

为解决现有入侵检测系统规则库维护管理复杂，系统检测效率不足等问题，设计了一种基于改进K均值聚类的规则挖掘算法。首先针对传统k-means算法聚类数目不确定的问题，通过分析聚类数目与簇间距离、簇内距离的关系，引入动态函数确定最佳聚类数目；然后通过寻找数据密集区域避开离群点，优化了初始聚类中心的选择，提高了算法效率。采用改进k-means聚类的入侵规则挖掘算法能够快速有效的对大数据集进行聚类分析，解决了传统入侵检测系统规则库维护复杂、难于检测未知攻击等问题。

入侵检测；数据挖掘；k-means算法；聚类分析；规则库

Class NumberTP393

1 引言

传统入侵检测系统（Intrusion Detection System，IDS）主要依据入侵模式和攻击特点提取攻击特征库，在检测效率和智能性上明显不足。而随着网络技术的不断发展，网络带宽快速提高，攻击手段高超多样，攻击特征很难捕捉。因此采用传统的网络入侵检测技术，难以有效检测各种网络渗透和攻击。我们认为：一方面随着网络带宽的提高，网络数据具有数量大、流速快、类型多等特点，具有典型的大数据特征；另一方面一种新型的网络攻击技术，极可能是某种已知攻击技术的发展，或者是若干已知攻击技术的创新性的组合运用。因此，可以采用数据挖掘（Data Mining，DM）技术，对网络数据流进行分析，分别建立正常行为规则库和攻击行为规则库，从而对入侵行为进行检测和预警。目前，国内外学者都在致力于将数据挖掘应用于入侵检测系统，主要涉及基于数据挖掘的入侵检测模型［1］和入侵检测方法［2～4］。DM+IDS已成为入侵检测领域的一个重要研究方向［5～11］。本文通过对传统k-means算法聚类数目不确定和随机选择初始聚类中心等缺陷进行改进；然后利用改进的k-means聚类算法进行规则挖掘。有效解决了传统入侵检测系统规则库维护复杂、难于检测未知攻击等问题。

2 传统K均值算法缺陷分析

K均值算法是1967年由J.B.MacQueen提出的一种基于划分的聚类方法。由于该算法简单、高效、适用于大数据的处理，被广泛应用于各个领域。K均值算法只需要输入聚类个数k一个参数，就可以自行将Rd空间上的数据集X=｛x1，…，xi，…，xn｝划分到K个不同类或簇之中，使得聚类结果中簇间相似度尽可能小，簇内相似度尽可能大。

K均值算法的处理流程：首先从给定的数据集X中随机指定K个数据点作为初始聚类中心，即初始簇中心；对于数据集中其它数据点通过计算其与各个初始聚类中心的距离，将其划分到与之最近的聚类中心所属的簇中；然后通过计算各簇中所有数据对象的平均值，调整各簇的聚类中心，更新其它点的所属簇，如此反复迭代，直至目标函数收敛。

一般采用均方差作为目标函数，其具体定义如下：

其中，x为数据集中的一个对象，Ci为一个簇，为Ci的中心，即Ci中所有对象的均值。

k-means算法描述，如下。

输入：数据集x，簇个数k；

输出：目标函数收敛的k个簇；

Step1：从给定的数据集X中随机指定k个数据点作为初始聚类中心；

Step2：将剩下的数据对象划分到与之最近的簇Ci中；，其中||ci是第i个簇中包含的数据个数；

Step4：循环Step2到Step3直到目标函数收敛。

Step3：计算新的簇中心：

K均值算法虽然简单高效，但也有其本身的缺陷：

1）聚类个数k需要手动输入。在聚类分析之前，k-means算法假定聚类数目k是已知的，但实际上很难确定k值。

2）初始聚类中心的选择是随机的。传统的k均值算法随机选择初始中心，然后进行迭代；选择不同的迭代起点，对应的搜索路径各不相同。致使最终的聚类结果容易陷入局部最优而非全局最优。

3）噪声和离群点对聚类结果有重大影响。由于算法的每次迭代，都会根据各簇中的数据属性计算该簇的中心点，噪声和离群点的存在，势必会干扰簇中心的计算，影响聚类的结果。

3 K均值算法的改进

针对前一节中对k-means算法的缺陷分析，本文主要从聚类数目和初始聚类中心选择两个方面进行优化。首先，确定最合适的聚类数目。聚类数目太少，簇内距离太大，各簇划分的太笼统，看不清楚各数据类的特征；聚类数目太多，簇内距离太小，各簇划分的太细碎，对数据集的认识只限于各小类，缺乏整体认识。其次，确定初始聚类中心。分析可知，真实的聚类中心应该分布在数据相对集中密集的地方，且每个聚类中心应该有一定的距离。如果初始聚类中心离真实聚类中心越近，迭代的次数越少，目标函数收敛的越快，可以提高聚类算法的效率和准确性。

3.1 相关概念与定义

设X=｛x1，…，xi，…，xn｝是一个包含n个对象的Rd空间上的数据集。

定义1：簇间距离：各簇中心到样本数据集X中心的距离。

定义2：簇内距离：各簇内所有数据到其中心的距离之和。

其中，Di为第i个簇的簇内距离，为簇Ci的中心，x为其中数据。

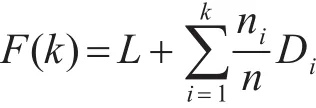
定义3：动态函数：簇间距离与加权的簇内距离之和。其中F(k)为动态函数，L、D、k的含义与式（1）、式（2）相同，ni为簇Ci中含数据个数，n为X中数据总个数。

3.2 聚类数目的确定

k-means算法假定聚类数目k是已知的，但实际上很难确定k值，而聚类个数的选取对聚类结果非常关键。因此，本文采用动态函数对聚类数目的选取进行优化。动态函数F(k)分为两个部分，其中L是关于k的增函数；Di是关于k的减函数，F(k)的变化取决于二者的合成。分析可知，当F(k)的值最小时对应的k值即为最佳聚类数目。

首先，聚类数目过多过少都是不合常理的，不能够清楚表达各簇特征。确定聚类数目k的最佳范围［kmin，kmax］，就是要确定k的最小值kmin和最大值kmax。若kmin=1，代表样本均匀分布，无明显特征差异，则不用进行聚类，所以一般k的最小值kmin=2；对于kmax确定，目前尚没有明确方法，一般使用经验规则kmax≤n［12］，韩凌波在k均值算法中聚类个数优化问题研究［13］中也指出该规则是合理的，本文采用上述规则来确定k的取值范围。

然后，对k∈[] 2，n上所有值分别进行聚类，

计算其动态函数F(k)的值。当F(k)最小时，对应的k值即为最佳聚类数目，记为k*。

3.3 初始聚类中心选择算法

为了使选取的初始聚类中心更接近真实的聚类中心，改进算法首先计算每个数据点的紧密程度，对较为稀疏的独立数据点进行标记，同时找出密集程度高的数据点集合。然后在数据密集区域内，选择一个点，要求它和与之相邻的t个数据点的距离之和最小，作为第一个初始聚类中心；接着在该区域内选择距离第一个初始聚类中心最远的点作为第二个初始聚类中心；依次选择与已选取的初始聚类中心最小距离中最大的数据点作为下一个初始聚类中心［14］，直到第k个。这样可以充分保证初始聚类中心的均匀分布。

下面详细介绍选择初始聚类中心的改进算法，如下。

输入：数据集X，聚类个数k，最近邻个数t；输出：k个初始聚类中心；

Step1：对于数据集X={x1，…，xi，…，xn}中的每一个数据点xi，求出与之相邻的t个数据点的距最近邻数据点集合；

Step3：在N中，取Si最小的xi为第一个初始聚类中心c1；取距离c1最远的数据点作为第二个初始聚类中心c2；第m（3≤m≤K）个初始聚类中心cm为满足以下条件的数据点xi，xi∈N，max(Dmin(xi，c1)，Dmin(xi，c2)，…，Dmin(xi，cm-1))其中i=1，2，…，n，即xi为与已选取的初始聚类中心最小距离中最大的数据点。直至得到第K个初始聚类中心。

通过该算法选择的初始聚类中心，首先，排除了噪声和离群点的干扰，保证了聚类算法的迭代起点不会过多的偏离真实聚类中心，减少了算法的迭代次数；其次，依据数据的密集程度选择初始聚类中心，有利于快速找到真实聚类中心，提高算法效率；最后，根据最大距离和原理，保证了初始聚类中心的均匀分布。

4 基于改进K均值聚类的规则挖掘算法

4.1 数据预处理

由于每条数据的数据值型属性的波动范围较大，往往会出现“大数”吃“小数”的现象，所以要对数值型数据进行标准化和归一化处理；对于符号型属性，不能直接进行比较，必须先对其进行赋值，然后进行标准化和归一化。对于d维数据集X={x1，x2，…，xn}，数据预处理步骤如下［6］：

1）数值规范化处理

其中Averj是指第j个特征的平均值，是指第j个特征的平均绝对偏

2）数值的归一化处理

归一化处理就是将数据值变换到［0，1］区间上来，设x''ij为经归一化处理之后的数值：，其中∀i，xmin是j属性的最小值，xmax是j属性的最大值。

4.2 规则挖掘算法

k均值算法的最大特点就是能够方便快捷地处理大数据集，由于正常网络数据量明显大于攻击数据量，而且正常网络数据与攻击数据在某些属性上的不同，因此可以将捕获的网络数据划分为不同的类，通过设置阈值来检测攻击数据。然后分别将正常数据和攻击数据增加到正常行为规则库和攻击行为规则库。但k均值算法本身有许多不足之处，并不能直接应用［14-16］。本文通过分析该算法的特点，设计了一种基于改进k-means聚类的入侵规则挖掘算法，算法描述如下。

输入：d维数据集X={x1，x2，…，xn}，聚类收敛精度ε，最近邻个数t；

输出：k个数据簇中心C={c1，…，cj，…，ck}，异常规则库U，正常规则库N；

Step1：令初始聚类准则函数值J0=0，每个数据点xi的异常度Axi=0，i=1，2，…，n；

Step2：对于数据集X={x1，…，xi，…，xn}中的每一个数据点xi，求出与之相邻的t个数据点的距离之和，其中Gt(xi)为xi的t个最近邻数据点集合；

Step4：在N中，取Si最小的xi为第一个初始聚类中心c1；取距离c1最远的数据点作为第二个初始聚类中心c2；第m（3≤m≤K）个初始聚类中心cm为满足以下条件的数据点xi，xi∈N，（i=1，2，…，n）：max(Dmin(xi，c1)，Dmin(xi，c2)，…，Dmin(xi，cm-1))，即xi为与已选取的初始聚类中心最小距离中最大的数据点。直至得到第K个初始聚类中心；

Step7：在形成的K个簇的过程中，若属于该簇的数据点与该簇聚类中心距离的大于平均距离，即是第j个簇中包含的数据个数，则Axi++；

Step8：若Ax≥3，则判断x为异常点，将其从集合N中删除，并入集合U中；

5 结语

本文通过分析传统k-means算法聚类数目不确定，随机选择初始聚类中心等不足。首先通过分析聚类数目与簇间距离和簇内距离的关系，引入动态函数找出了最佳聚类数目。然后通过寻找数据密集区域避开离群点区域，优化了k均值算法的初始聚类中心选择。最后设计了一种基于改进K均值聚类的入侵规则挖掘算法，该算法能够快速有效的对大数据集进行聚类分析，解决了传统入侵检测系统规则库维护管理困难的问题。

［1］Li Y，Li J L，Yue S J，et al.Research of Intrusion Detection Based on Ensemble Learning Model［J］.Applied Mechanics and Materials，2013，336：2376-2380.

［2］Fatma H，Mohamed L.A two-stage technique to improve intrusion detection systems based on data mining algorithms［C］//5th International Conference on Modeling，Simulation and Applied Optimization（ICMSAO）.IEEE，2013：1-6.

［3］Kim G，Lee S，Kim S.A novel hybrid intrusion detection method integrating anomaly detection with misuse detection［J］.Expert Systems with Applications，2014，41（4）：1690-1700.

［4］Khor K C，Ting C Y，Phon-Amnuaisuk S.A cascaded classifier approach for improving detection rates on rare attack categories in network intrusion detection［J］.Applied Intelligence，2012，36（2）：320-329.

［5］刘华春，候向宁，杨忠.基于改进K均值算法的入侵检测系统设计［J］.计算机技术与发展，2016，26（1）：101-106.

LIU Huachun，HOU Xiangning，YANG Zhong.Design of Intrusion Detection System based on Improved K Algorithm［J］.Computer Technology and Development，2016，26（1）：101-106.

［6］程晓旭，于海涛，李梓.改进的k-means网络入侵检测算法［J］.智能计算机与应用，2012，2（2）：21-23.

CHENG Xiaoxu，YU Haitao，LI Zi.Improved K-means Network Intrusion Detection Algorithm［J］.Intelligent computer and Application，2012，2（2）：21-23.

［7］刘长骞.K均值算法改进及在网络入侵检测中的应用［J］.计算机仿真，2011，28（3）：190-193.

LIU Changqian.Improvement of K mean Algorithm and its Application in Network Intrusion Detection［J］.Computer Simulation，2011，28（3）：190-193.

［8］储泽楠，李世扬.基于节点生长马氏距离K均值和HMM的网络入侵检测方法设计［J］.计算机测量与控制，2014，22（10）：3406-3410.

CHU Zenan，LI Shiyang.Design of Network Intrusion Detection Method based on the K Mean Value and HMM of the Node Growth Markov Distance［J］.Computer Measurement and Control，2014，22（10）：3406-3410.

［9］易倩，腾长华，张巍.基于马氏距离的K均值聚类算法的入侵检测［J］.江西师范大学学报，2012，36（3）：284-288.

YI Qian，TENG Changhua，ZHANG Wei.Intrusion Detection Based on K mean Clustering Algorithm based on Markov Distance［J］.Journal of Jiangxi Normal University， 2012，36（3）：284-288.

［10］郭春.基于数据挖掘的网络入侵检测［D］.北京：北京邮电大学，2014.

GUO Chun.Network Intrusion Detection based on Data Mining［D］.Beijing：Beijing University of Posts and Telecommunications，2014.

［11］韩占柱.改进k-means算法的网络数据库入侵检测［J］.微电子学与计算机，2012，29（3）：144-150.

HAN Zhanzhu.Intrusion Detection of Network Database based on Improved K-means Algorithm［J］.Microellectronics&Computer，2012，29（3）：144-150.

［12］Ramze R M，Lelieveldt B P F，Reiber J H C.A new cluster validity indexes for the fuzzy c-means.Pattern Recognition Letters，1998，19（1）：237-246.

［13］韩凌波.K均值算法中聚类个数优化问题研究［J］.四川理工学院学报，2012，25（2）：77-80.

HAN Lingbo.Research on Clustering Number Optimization in K mean Algorithm［J］.Journal of Sichuan University of Science and Engineering，2012，25（2）：77-80.

［14］TZORTZIS G，LIKAS A.The minmax k-means clustering algorithm［J］.Pattern Recognition，2011，44（4）：866-876.

［15］蒋大宇.快速有效的并行二分K均值算法［D］.哈尔滨：哈尔滨工程大学，2013.

JIANG Dayu.Fast Efficient Parallel Two K mean Algorithm［D］.Harbin：Harbin Engineering University，2013.

［16］朱建宇.K均值算法研究及其应用［D］.大连：大连理工大学，2013.

JIANG Dayu.Research and application of K mean algorithm［D］.Dalian：Dalian University of Technology，2013.

Intrusion Detection Algorithm Based on Improved K-means Clustering

HE Mingliang1CHEN Zemao1HUANG Xiangjing2
（1.Information Security Department，Naval University of Engineering，Wuhan430033）（2.No.91681 Troops of PLA，Ningbo315731）

In order to solve the problems of the existing intrusion detection system，such as the complexity of the maintenance and management of the rule base，the lack of the detection efficiency of the system，an intrusion rule mining algorithm based on improved K mean clustering algorithm is designed.Firstly，according to the problem that the traditional K-means algorithm is not sure of the number of clusters，by analyzing the relationship between the number of clusters and the distance between clusters and inter clusters，the dynamic function is introduced to determine the optimal number of clusters.Then，the selection of initial cluster centers is optimized by finding the data intensive regions to avoid outliers，which improves the efficiency of the algorithm.The intrusion rule mining algorithm based on improved k-means clustering algorithm can quickly and effectively do cluster analysis on large data sets，and solve the problems of traditional intrusion detection system，such as the complexity of rule base and difficulty of detecting unknown attacks.

intrusion detection，data mining，k-means algorithm，clustering analysis，rule base

TP393

10.3969/j.issn.1672-9722.2017.06.028

2016年12月7日，

2017年1月18日

湖北省自然科学基金资助项目（编号：2015CF867）资助。

何明亮，男，硕士，研究方向：信息安全。陈泽茂，男，博士，教授，研究方向：网络安全。黄相静，男，研究方向：信息安全。