CSSAQP：一种基于聚类的分层抽样近似查询处理算法

谢金星李晖陈梅戴振宇

（贵州大学先进计算与医疗信息服务工程实验室贵阳550025）

CSSAQP：一种基于聚类的分层抽样近似查询处理算法

谢金星李晖陈梅戴振宇

（贵州大学先进计算与医疗信息服务工程实验室贵阳550025）

近似查询处理技术常被应用于海量数据的多维分析，以缩短查询执行的时间，同时返回尽可能准确的结果。由于海量数据中常存在许多极端值，会严重影响近似查询处理的结果。因此针对海量数据的聚集操作，论文提出CSSAQP算法，先将原始数据集按某一数值列直观的聚为三类，分别代表大值簇、小值簇和常值簇，再对各簇按分组属性分别进行分层抽样，构建总体样本集，最后通过查询重写在总体样本集上执行查询，以缩短海量数据聚集操作的查询时间，同时提高查询任务的准确性。通过实验验证，证明了该算法不仅可以缩短聚集查询的时间，同时还能有效提高查询结果的精度。

近似查询处理；聚集查询；聚类；分层抽样

Class NumberTP311.13

1 引言

对海量数据进行多维分析，常伴随大量的聚集操作，如在一个或多个维度上进行group-by聚集查询，通常需要较长的执行时间。而在进行业务分析时，用户往往仅需了解大致的趋势，查询的响应时间相对于完全准确的查询结果更为重要。因此为了快速返回分析结果，可以将数据仓库中常使用的近似查询处理技术，应用到该类场景中，在缩短查询执行时间的同时，提供一个尽可能精确的近似结果。

近似查询处理有两类基本方法：联机查询处理和预计算方法［1］。前者不需要预先进行数据处理，在查询执行过程中对数据进行动态抽样，动态计算和聚集返回当前近似结果和置信区间；后者是对数据库中的数据事先进行预处理，生成能代表原来数据并且数据量小得多的样本集或初步聚集结果，在查询时使用这些数据集合获取近似结果。常使用的具体技术有：直方图、小波变换、抽样等［2］。

在对海量数据近似查询处理时，常使用抽样技术。通过抽取部分能代表整体数据集特征的子集，在该子集上执行查询，并将查询结果按照抽取比率放大，以此作为整体数据集上查询结果的近似值。

由于海量数据中通常存在许多极端值的情况，将严重影响近似处理的效果。为进一步提高近似结果的准确性，本文采用预计算样本的方式，提出基于聚类的分层抽样算法。直观上将某一数值列聚为三类，分别代表大值簇、小值簇和常值簇，再根据聚类结果对各个簇按照分组属性分层抽样，构建总体样本集。最后通过查询重写在总体样本集上执行查询，并返回查询结果。既缩短了多维分析任务的执行时间，又提高了任务的准确度。

本文工作如下：

1）研究了基于抽样的近似查询处理技术，并介绍各自的适用情况；

2）针对海量数据group-by的聚集查询，提出基于聚类的分层抽样近似查询处理算法；

3）利用TPC-H生成测试数据，对聚集查询进行实验测试；

4）对实验结果进行分析。

2 基于抽样的近似查询处理技术

所谓近似查询处理技术，就是对提交的查询给出一个近似的合理的查询结果。其基本思路是通过查询更少量的数据，获取尽可能准确的结果。

本文重点讨论近似查询处理技术中的抽样技术。抽样技术的基本思想是：通过适当的方法，从海量原始记录中按一定比率抽取能代表整体数据特征的子集，构建样本集。通过在样本集上执行查询，并将查询结果按抽样比率等比例放大，就可获得与准确值的估计值。

抽样技术的难点在于如何制定合适的抽样条件，以构建能代表整体数据特征的样本集。其结果的精度可能受到查询类型、查询选择率、数据分布和样本大小等因素的影响。常用的抽样技术主要有：简单随机抽样、偏倚抽样、分层抽样、国会抽样等［3～4］。

2.1 简单随机抽样

按照等概率的原则，简单随机抽样直接从含有r条记录的原始数据集中随机抽取s（s≤r）条记录，构成样本集，适用于数据均匀分布的情况。其优点是简单易操作。但是在真实的生产环境下，数据往往非均匀分布，具备较大的数据倾斜，简单随机抽样会导致较大的误差。另外，在查询选择率较低时，如处理涉及group-by的查询，在简单随机抽样构建的样本集中，记录数比较少的组不能够得到充分的体现，会造成数据量较少的组查询结果严重失真［5］。

在简单随机抽样过程中，为了保证每条记录被抽中的概率相等，可使用伯努利抽样或蓄水池抽样。

2.2 偏倚抽样

针对简单随机抽样的不足，出现了偏倚抽样，每条记录被抽到的概率可能不同。偏倚抽样结合以往分析任务的信息（如历史查询、查询日志），可以很好预测将来的查询，因此可以加大相对重要记录的抽取比例，降低相对不重要记录的抽取比例。

偏倚抽样和简单随机抽样是其他抽样技术的基础。

2.3 分层抽样

分层抽样按照某些规则或某种特征，将原始数据集划分成互不重叠的若干层，在每层内独立、随机地抽样。假设总体被分为d层，总体样本S大小为|S|，第i层的样本大小为Si，则|S|=S1+S2+…+ Si+…+Sd，即总体的样本由每层抽取的样本构成。因此总体指标的估计值可由每层样本估计值汇总求得。所以分层抽样既可以对各层的指标进行估计，也可以对总体指标进行估计。

使用分层抽样技术，可以在不增加样本大小的前提下，提高查询结果的精度，降低抽样的误差。但是，需要掌握查询的一些信息，并基于此确定分层的标准［6～7］。

2.4 国会抽样

在分析任务中，常伴随大量的聚集查询。国会抽样是针对带group-by的聚集查询所提出，其主要思想是根据group-by可能涉及的属性将原始数据分割为若干组，在总体样本量已确定的前提下，每组利用随机抽样，抽取一定量的分样本，并由分样本构成总体样本。

在基本国会抽样中，为了更合理的分配各组样本数，使样本总体和分组样本上执行的查询结果达到较小误差，第g分组抽取的样本数Sg公式如下［8］：

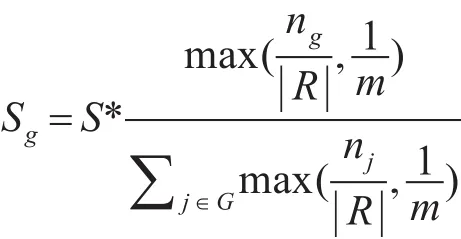
表1 参数说明

3 CSSAQP算法设计

用近似查询处理技术处理海量数据的聚集操作，常面临数据倾斜的问题。海量原始数据中存在一些严重影响聚集查询结果的记录，即极端值。由于极端值的存在，使得对原始数据进行简单随机抽样获取的查询结果可能会严重偏离真实值，导致很大的误差。因此本文提出基于聚类的分层抽样近似查询处理算法。先利用k-means聚类算法，按某个数值属性将原始记录直观地划分为大值簇、小值簇、常值簇三个簇，再对三个簇按照分组属性分别分层抽样，构建总体数据集的样本集；最后通过查询重写，在总体样本集上执行查询，返回近似结果。

3.1 极端值问题描述

假设关系R含字符属性ItemNO，指标属性Profit共4条记录，如下所示：

关系R：

Record：｛<1，800>，<2，900>，<3，800>，<4，10000>｝

查询Q：SELECT AVG（Profit）FROM R

采用随机抽样技术，抽取两条记录构成样本集并执行Q。假设构成的随机样本S1为：｛<1，800>，<3，800>｝。原始记录查询结果Result=3125，S1上的近似结果Result'=800。由于极端值的存在，严重影响了近似查询的结果。

3.2 CSSAQP算法

为了克服极端值对基于抽样的近似查询结果的影响，本文针对带group-by的聚集操作提出基于聚类的分层抽样近似处理算法CSSAQP。

预构建样本集，需假设已知将来分析任务的一些信息。通过研究发现，分析任务中的查询所涉及的列（如分组属性列）通常比较稳定，在将来的查询中也有很大的概率被用于构建查询［9～10］。对关系表R，可将属性划分为字符属性C和指标属性V，其分组属性G⊂C。在进行数据分析时，分析人员也通常已知需要计算的指标属性。因此我们假设查询的分组属性和指标属性已知。

指定关系表R、分组属性G、指标属性V、抽样率f，CSSAQP即可构成样本集S，当查询到来时可通过查询重写在S上执行查询，并返回真实值的近似结果。

CSSAQP分为两个阶段，分别为预构建样本阶段和查询执行阶段，如图1所示。

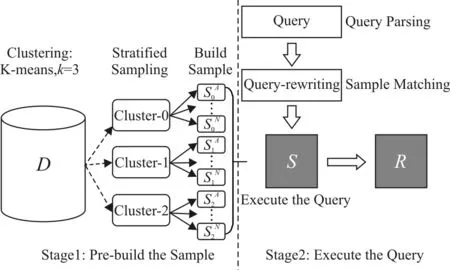
图1 CSSAQP算法图解

第一阶段：预构建样本阶段

利用K-means聚类算法将R按照V划分为3个簇，各簇内再根据分组属性G划分为互不相交的若干层，然后在各层内按抽样率f随机抽样，构建总的样本表S。

第二阶段：查询执行阶段

当查询到来，经过查询解析层获取查询语句Q中涉及的G、V，再通过样本选择器匹配相应的S并执行查询，输出查询结果的近似值；如果样本匹配失败，则在R上执行查询，输出查询结果的准确值。

表2 CSSAQP算法的主要符号及含义，表3算法1：CSSAQP的伪代码表述。

表2 CSSAQP算法符号说明

表3 算法1：CSSAQP伪代码表述

4 实验结果与分析

4.1 实验环境

本实验在CentOS7操作系统上，搭建Hadoop集群，该集群包括1个master节点（用以运行namenode与jobtracker服务）和4个slave节点（用以运行datanode与tasktarcker服务），在此集群上搭建了Hive系统。集群中各个节点配置相同，均搭建在一个机架上。每个节点详细软件、硬件配置如表4所示。

表4 节点软硬件配置

4.2 实验分析

4.2.1 实验设计

本文通过TPC-H生成测试数据。TPC-H定义了8张表，共22条查询。可以通过设置scale参数生成总体数据量为指定大小的数据集，如设置salce=30，则生成总量为30G的数据。同时TPC-H还可以只生成某一张表［11］。

本实验设置scale分别为1、5、15、30、50，只生成lineitem事实表，用以对多维分析中常用的带group-by的聚集函数sum（）、avg（）进行测试，并从查询结果的准确性和查询执行的时间两个方面验证算法的有效性。

由于对多个指标属性的聚集查询，可以分解为多次单指标属性的聚集查询，因此定义以下查询：

Q1：select l_returnflag,l_linestatus,sum(l_quantity)as sum_qty from lineitem group by l_returnflag, l_linestatus；

Q2：Select l_returnflag,l_linestatus,avg(l_quantity)as avg_qty from lineitem group by l_returnflag, l_linestatus；

在准确性验证实验中，数据分布对基于抽样的近似处理结果影响很大，而TPC-H生成的数据服从均匀分布，因此在实验开始前，先对数据进行预处理。

通过观察发现TPC-H生成的lineitem表，其l_quantity属性取值为1-50的整数值，由于服从均匀分布，每个值的数量大致相同。因此通过计算1-50正态分布的概率（平均值=25.5，方差=14.6），再与其对应数量做乘积，获得1-50内大致服从正态分布的数据集，分别得到1200000～60000000条不等的五组数据，按1%的抽样率对随机抽样（RS）、分层抽样（SS）、聚类抽样（CS）、聚类分层抽样（CSS）构建样本集，进行试验对比。CS是直接将聚类结果进行随机抽样，即对聚类所得的簇分别进行随机抽样，对应算法1中分组属性为ϕ的情况，为说明该种情况下CSSAQP算法设计的合理性，故此也将其加入对比实验。

衡量近似结果好坏的标准有许多，这里我们采用相对误差率（以下简称误差率）衡量误差的高低。假设分组i的准确聚集值为ci，其近似值为

ci

′，则ci的误差率εi定义如下［8］：

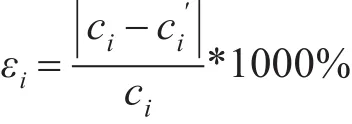
针对海量数据多维分析中含group-by的聚集操作，对其进行近似处理需要满足以下两个方面的要求：

一是近似查询的结果要包含所有的分组。由于CSSAQP会对分组属性先进行分层，并在各层内实施随机抽样，所以本条要求已具备。

二是每个分组的查询结果要尽可能准确。因此可用所有分组的近似结果的最大误差率来衡量整体近似结果的好坏。对含有n个分组的group-by聚集查询引用以下定义［8］：

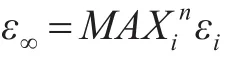
4.2.2 实验分析

Q1执行结果如图2所示。

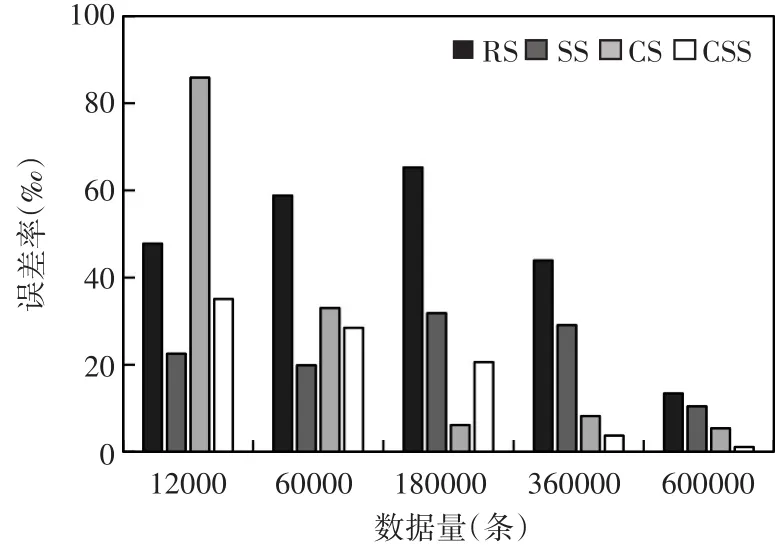
图2 Q1查询执行结果图

通过实验发现，总体而言随着数据量的增大，所有抽样算法的误差率都在逐步降低。说明在基于抽样的近似查询中，样本量越大，近似结果越好；同时，CS和CSS算法的结果，也随着数据量的增大逐步优于RS与CS抽样算法。验证了CSS算法在处理带group-by的sum（）聚集查询时具有一定的优势。

图3为Q2的执行结果。结果表明，对带group-by的avg（）聚集运算，随机抽样在所有算法中所造成的误差最大；随着数据量的增大，CSS和CS比RS与SS具有更高的准确性。

综合以上两个实验，随着数据量的增大，CS算法都有比较好的效果，同时CSSAQP的误差率明显低于RS和SS算法，从而验证了CSSAQP算法设计的合理性与有效性。

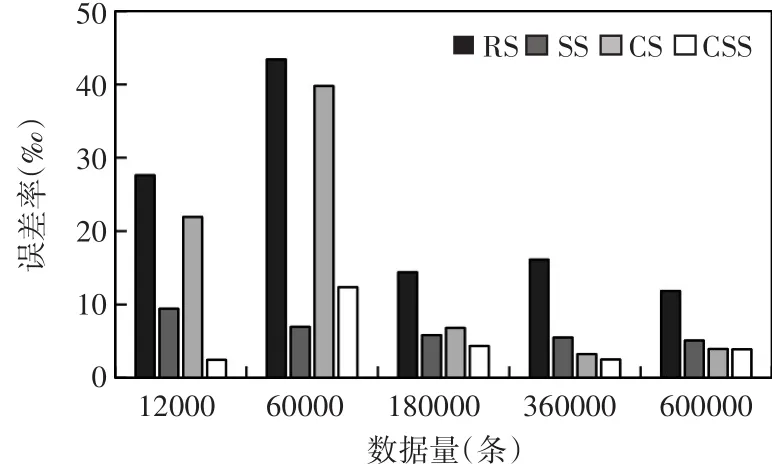
图3 Q2查询执行结果图

在执行时间有效性的验证中，准确值是在TPC-H生成的原始数据集上进行查询，数据量大小分别为0.76G、3.6G、11.59G、23.63G、39.53G，查询执行时间记作实际执行时间；近似结果是用CSSAQP算法按1%的抽样率构建的样本集求取，查询执行时间记作近似计算执行时间。由于各种抽样算法的查询执行时间大体相同，因此仅以CSSAQP和实际执行时间做比较，结果如图4、图5所示。

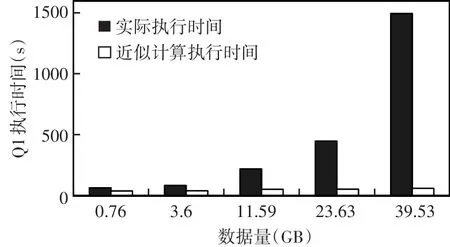
图4 Q1查询执行时间图

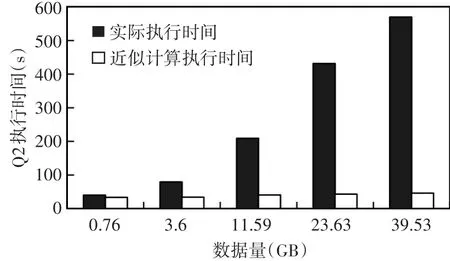
图5 Q2查询执行时间图

随着数据量的增大，所需的实际执行时间越来越长，且增幅较大。当数据量达到约11.59G时，Q1和Q2的实际执行时间已经超过200s；当数据量达到39.53G（集群总的内存大小）时，Q2的实际执行时间约10min，Q1的实际执行时间约25min。而使用CSSAQP算法的近似计算执行时间比较稳定，且远低于实际执行时间，从而证明了CSSAQP算法的时间有效性。

5 结语

在海量数据进行多维分析中，研究如何既快又准地获取分析结果是比较有意义的问题。本文提出基于聚类的分层抽样算法，并通过对比实验，从算法的时间有效性和结果准确性两个角度，验证该算法既能有效降低查询的执行时间，同时较之随机抽样、分层抽样算法又能提供一个更准确的近似结果。

［4］Liu Q.Approximate query processing［M］//Encyclopedia of Database Systems.Springer US，2009：113-119.

［5］Das G.Sampling methods in approximate query answering systems［M］//Encyclopedia of Data Warehousing and Mining，Second Edition.IGI Global，2009：1702-1707.

［6］Mehanna Y S，Mahmuddin M，Abdelaziz H S.Approximate Query Processing Concepts and Techniques［J］.Information Processing&Management，2015：453-468.

［7］金勇进，杜子芳，蒋妍.抽样技术.第3版［M］.中国人民大学出版社，2012.

J

IN Yongjin，DU Zifang，JIANG Yan.Sampling Technology.3rd edition［M］.Renmin University of China Press，2012.

［8］Acharya S，Gibbons P B，Poosala V.Congressional samples for approximate answering of group-by queries［C］// ACM SIGMOD Record.ACM，2000，29（2）：487-498.

［9］Ganti V，Lee M L，Ramakrishnan R.ICICLES：Self-Tuning Samples for Approximate Query Answering［C］// VLDB.2000，176（187）.

［10］Agarwal S，Mozafari B，Panda A，et al.BlinkDB：queries with bounded errors and bounded response times on very large data［C］//Proceedings of the 8th ACM European Conference on Computer Systems.ACM，2013：29-42.

［11］http：//www.tpc.org/tpch/

［1］冯玉.数据仓库环境中近似查询处理技术研究［D］.北京：中国科学院研究生院（计算技术研究所），2002.

FENG Yu.Study on Approximate Query Processing Technology in Data Warehouse Environment［D］.Beijing：Graduate School of Computing Technology（Institute of Computing Technology），2002.

［2］高雅卓.多维联机分析处理中的高效查询关键方法研究［D］.合肥：合肥工业大学，2012.

GAO Yazhuo.Research on Key Methods of High Efficiency Query in Multi-dimensional Online Analysis and Processing［D］.Hefei：Hefei University of Technology，2012.

［3］Madria S K，Mohania M，Roddick J F.APPROXIMATE QUERY PROCESSING［J］.Information Organization and Databases：Foundations of Data Organization，2012，579：207.

CSSAQP：An Approximate Query Algorithm Based On Clustering Stratified Samping

XIE JinxingLI HuiCHEN MeiDAI Zhenyu
（Guizhou Engineering Lab for ACMIS，Guizhou University，Guiyang550025）

The approximate query processing technique is often applied to multidimensional analysis of massive data to shorten the execution time of the query and return the results as accurate as possible.Because of many extreme values in massive data，it will seriously affect the results of approximate query processing.Therefore，for the aggregation of massive data，this paper proposes a algorithm CSSAQP，which first clustered the original data set into three categories by a column，representing large clusters，small clusters and constant clusters，then use stratified sampling for each cluster by the group attribute，and constructed the overall sample，finally，the query is rewritten on the overall sample set to reduce the query time of the massive data aggregation operation，and improve the accuracy of the query task.Experiments show that the algorithm can not only shorten the time of aggregation query，but also improve the accuracy of query results.

AQP，aggregate query，clustering，stratified sampling

TP311.13

10.3969/j.issn.1672-9722.2017.06.023

2016年12月1日，

2017年1月27日

国家自然科学基金项目（编号：61462012，61562010，U1531246）；基于云计算的医疗信息管理系统关键技术研究及应用（编号：GY［2014］3018）；贵州省重大应用基础研究项目（编号：JZ20142001）；贵州省教育厅自然科学项目（编号：黔科合人才团队字［2015］53号）；贵州大学研究生创新基金（院级）资助。

谢金星，男，硕士研究生，研究方向：大数据管理与应用。李晖，男，副教授，硕士生导师，研究方向：大规模数据管理与分析，高性能数据库，云计算。陈梅，女，硕士生导师，研究方向：数据库技术、计算机应用技术。戴震宇，男，实验师，研究方向：数据库技术、计算机应用技术。