基于P稳定分布局部敏感哈希的太赫兹光谱检索
(1.昆明理工大学信息科学与自动化学院昆明650500)(2.昆明理工大学智能信息处理重点实验室昆明650500)
基于P稳定分布局部敏感哈希的太赫兹光谱检索
李灵杰1,2沈韬1,2倪家鹏1,2
(1.昆明理工大学信息科学与自动化学院昆明650500)(2.昆明理工大学智能信息处理重点实验室昆明650500)
太赫兹光谱近似最近邻检索方法是太赫兹光谱充分利用和相关研究中的关键问题。目前,国内外均没有“以谱检谱”的太赫兹光谱数据库可供检索与查询。为此,论文结合基于随机投影的哈希算法优点,提出了一种基于P-stable分布的局部敏感哈希算法的太赫兹光谱检索方法。首先通过S-G滤波和3次的样条插值及重采样,对16种物质在0.9THz~6THz的太赫兹透射光谱进行归一化处理;然后用基于随机投影法的P-stable LSH对以上太赫兹光谱进行训练,把高维光谱数据降维映射到汉明空间,形成大小仅几十bit的哈希编码;最后选取每种物质的部分光谱作为查询光谱分别进行检索,计算查询光谱与数据点库哈希码间汉明距离,排序并返回结果。对比实验结果表明,使用P-stable的局部敏感哈希算法的检索结果更准确且效率更高,平均准确率的平均值高于其他有代表性的基于随机投影的哈希算法。
太赫兹光谱;光谱检索;随机投影;P稳定分布;局部敏感哈希
Class NumberTP391
1 引言
太赫兹光谱是指频率在0.1THz~10THz内的电磁波,物质的太赫兹光谱中有许多理化信息[1],当物质种类不同时,它们的光谱特征也是有差异的,这种“指纹谱”特性已经成为人们利用太赫兹光谱来研究和识别不同物质的重要依据[2~4]。近年来,随着太赫兹相关技术的不断突破,很多未被测量的物质的太赫兹光谱不断被发布,陆续有国内外研究者和机构建立太赫兹光谱数据库并供公开使用,如文献[5]构建了由17种爆炸物及其相关化合物组成的太赫兹光谱数据库;美国标准技术组织(NIST)及欧洲“THz-Bridge”项目组分别在其网站上公布了部分食品、药物、化学材料及生物大分子的太赫兹光谱数据[6~7];日本国家通信与信息中心的(RIKEN)和日本理化研究所(NICT)整理了现有的太赫兹光谱,并开发了一个包含1000多种太赫兹光谱的在线数据库[8],具有列表和名称关键字查询功能。以上数据库包含的检索功能是通过人工标注光谱标签,并由标注好的光谱和对应的物质名称关键词组成检索数据库。这种基于文本的太赫兹光谱检索方式实质上还是文本搜索,由于目前尚无针对规模化太赫兹光谱的效率足够高的检索算法,导致这些数据库的光谱利用率很低,大量的太赫兹光谱数据不能得到充分利用和进一步的研究。随着光谱数据不断增多,对未知光谱的识别和研究需求不断增加,太赫兹光谱的图谱检索相关研究具有非常重要的作用。为了解决以上问题,本文提出基于内容的太赫兹光谱检索方法,即“以谱检谱”方法。
太赫兹光谱的处理与图像、音频和文本等领域类似,研究的对象都是规模庞大的高维度数据。由于维度灾难(Curse of Dimensionality),这些规模化的高维数据的最近邻检索是很难实现的,基于树索引的传统技术会随着数据维数的增多而性能急剧下降,现如今的树索引方法均不能很好地解决大规模高维数据的检索问题。但在实际应用中,需要的是更高的效率,近似的光谱数据即可满足需求。因此,各种近似最近邻查找(Approximate Nearest Neighbor,ANN)算法陆续被学者们提出[9~11]。
本文采用的是基于P稳定分布的局部敏感哈希(P-stable Locality Sensitive Hashing,P-stable LSH)检索算法[12~13],属于ANN算法。LSH是图像等高维数据检索中最著名有效且常用的方法,已在高维数据中取得了相当于k-d树等方法在低维数据中的优越性。目前,LSH已经被广泛地运用于各种检索领域,如文本、音频、图片、视频、基因等[14~15]。LSH能以恒定不变的概率保证返回的数据是真实最近邻或近似最近邻,其基本思想是用哈希函数值确保近似数据点以很高的概率发生冲突并被检测到。在此基础上,本文首先对太赫兹光谱数据点集进行P-stable哈希函数的哈希映射实现降维,再对降维后的特征向量进行二值化哈希编码,最后查询时将查询光谱用相同的哈希函数映射并压缩成二值编码,所有的光谱数据点集的哈希编码与查询点按照汉明距离的大小来排序,并返回前k个结果。该方法在保证检索需要的准确率的同时,能有效解决规模化、高维度的太赫兹光谱数据在传统相似性度量的近邻检索效率问题。
2 相似性检索
太赫兹光谱数据等特征丰富的数据常被表示为高维特征向量,对于大规模的高维数据的相似性度量和检索,主要问题在于最近邻的获取。相似性搜索一般应用在K近邻(K-Nearest Neighbor,KNN)和近似近邻(Approximate Nearest Neighbors,ANN)搜索中。一个针对相似性搜索的理想索引策略需满足以下特性:
1)准确性:一个查询操作应该得到接近于线性搜索的理想返回结果;
2)时间效率:一个查询操作的时间复杂度应该是O(1)或者O(logN),其中N是数据集的数据数量;
3)空间效率:索引应该需要较少的内存空间,最好是和数据集数量差不多,不能比原始数据还要多;
4)高维度:索引策略应在高维空间中工作良好。
近邻的获取可以用如下形式表示:给定一个已知查询数据q,最近邻检索是要从数据集X={x1,x2,...,xn}∈ℝd×n中找到q∈ℝd的最近邻:

其中,d是查询数据的维度,dist(·)是衡量数据之间相似性的距离度量。
传统的近邻检索方法通常应用在低维数据,然而,面对大量的高维数据,准确检索出最近的若干近邻是不符合实际情况的。所以,近似最近邻的检索方法不断被提出,即允许近似最近邻检索算法返回的结果中有比最近邻距离不超过(1+ε)倍的数据点,其中ε是一个大于0的很小的数。相比于准确的最近邻检索,近似最近邻检索在能够保证检索效率的前提下,是更符合实际情况和普遍需要的方法。近些年,近似最近邻检索在许多应用中和确切搜索有一样好的效果,但查询时间更快。
3 基于P稳定分布局部敏感哈希的太赫兹光谱检索方法
3.1 局部敏感哈希
基于哈希的检索方法最早起源于局部敏感哈希[16],其目的在于通过哈希函数,把相近的点以尽可能高概率地映射成相同哈希值[17]。当要查询的时候,只需要计算与查询点哈希编码的汉明距离,从而减少距离计算,加快查询时间。局部敏感哈希函数家族Η,和一个哈希函数h属于Η的条件定义如下:对于一个点集的集合S和一个距离度量函数d,H={h:S→U},其中H是局部敏感的,对于任何v,q∈S:
1)如果v∈B(q,r1),则PrH[h(q)=h(v)]>p1;
2)如果v∉B(q,r2),则PrH[h(q)=h(v)]<p2。
那么就称函数h属于Η并且是(r1,r2,p1,p2)-敏感的。
其中,B(q,r)={v∈S|d(v,q)≤r},表示离点x距离在r范围内的区域。PrH为概率,p1>p2,r1<r2,算法将哈希数据点集P进行哈希映射到U,把相近的点以尽可能高的概率映射到相同的哈希桶中。
3.2 基于随机投影的哈希算法
使用随机投影是一种经典且实用的LSH方法。其中文献[18]提出了一种基于随机投影的二值哈希编码方法:
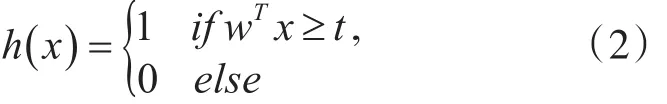
其中w为符合P-stable分布的随机超平面。该超平面把整个空间分成了两部分,定义其中满足条件wTx≥t的点哈希值为1,另一部分点的哈希值为0。
为了增加不同哈希值的个数,可以多次生成独立的函数h(·),只有当两个元素的多个h(·)值都相等时才算拥有相同的哈希值。根据该思路可以定义如下的哈希函数H(·):

其中每个h(v→)表示一个独立的h(·)函数,H(·)函
i数值的二进制表现形式中每一位都是一个h(·)函数的结果。
这个方法具有保角的性质,即:
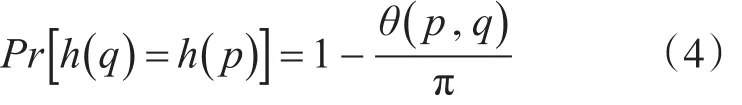
其中θ(p,q)是点p和点q的夹角。
3.3 P-stable分布
对于一个在实数集R上的分布D,如果存在p≥0,对于任意n个实数v1,…,vn和n个满足D布的一个随机变量,则称D为一个稳定分布。对任何p∈[0,2]存在稳定分布:1-稳定分布。
1)柯西分布:概率密度函数是2-稳定分布。
文献[19]首次提出用稳定分布来描述高维特征向量。稳定分布已经被广泛地应用在许多领域,如基于内容的图像与视频检索。利用P-stable可以有效的近似高维特征向量,并在保证度量距离的同时,对高维特征向量进行降维。P-stable的关键思想是,产生一个d维的随机变量a,a中的每一维都是从P-stable分布中随机、独立地产生;对于一个d维的特征向量v,随机变量a·v具有和随机变量)相同的分布。基于以上原因,可以用a·v表示向量v,并用来估计‖‖vp,得出a() v1-v2= a·v1-a·v2。
3.4 基于P稳定分布局部敏感哈希的太赫兹光谱检索方法
在基于P-stable分布的LSH算法[20]中,利用了P-stable的思想,结合随机投影理论,每个哈希函数定义为:映射一个d维特征向量v到一个二值化编码,哈希函数中有一个随机变量a,是一个独立选取的满足P-stable的随机变量,v为一个d维特征向量,则哈希函数为
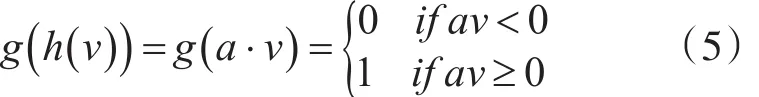
使用a·v对每一个向量v赋一个哈希值,很明显,这是一个局部敏感的哈希函数。因此对于两个向量v1和v2,如果它们距离很近,它们的哈希值相同的概率将会很大;如果它们距离很远,则哈希值相同的概率将会很小。
这样哈希函数g() a·v将一个d维空间向量映射为0或1的二值化编码。选择k个上述的哈希函数,进行k次二值化映射,即可得到一个k位的二进制编码,该编码即为哈希码。使用LSH函数直接将原始数据转换为哈希码后,利用哈希码来代替原始光谱数据进行存储。在计算相似度时使用码间汉明距离来衡量,不需要计算原始光谱数据的相似度,从而大大加快太赫兹光谱的检索效率。
经过前几节的分析,基于P-stable分布的LSH算法的哈希码编码过程可以归结为如下步骤:
1)初始化
构造L个函数g1(·),g2(·),.…,gL(·)其中h2(·),…,hk(·)是局部敏感哈希函数族中独立随机选取的哈希函数,由式(5)得出。
2)利用LSH映射降维
3)二值化编码
将降维后的L位二值化编码作为原始光谱数据的哈希码,并代替原始光谱数据进行存储。
对于给定的查询点q,相应的搜索算法描述如下:
(1)对哈希函数g,计算g(v);
(2)对数据点库对应的每一个哈希码逐一计算汉明距离;
(3)按照距离计算结果排序并取前k个作为查询结果。
4 实验结果及分析
4.1 实验数据
由于不同太赫兹光谱系统设定的带宽和采样频率等参数并不一致,以及受到实验条件的影响,最终获得的太赫兹光谱会含有噪声且光谱分辨率不尽相同。针对这些问题,首先利用S-G滤波器对太赫兹光谱进行滤波,然后截取相同频段的光谱,利用三次样条插值法得到统一分辨率的光谱数据。
实验以5-Acetylsalicylic Acid、Cisplatin、Fluorouracil、Ganciclovir、Lincomycin Hydrochrloride、Lumichrome、Palatinose、Salicylic Acid、Cadmium Selenide(CdSe)、Dicofol、Polyethylene spectrophotometric grade、Methidation(DMTP)、Poly(9-vinylcarbazole)、Pantothenate Calcium、Cadmium Sulfide(CdS)、Cypermethrin的太赫兹透射光谱为例,在0.9THz~6THz频段内,经过数据预处理后分别得到16种物质、每种物质120个太赫兹透射光谱样本,每条光谱曲线的数据点均为6349个。将16种物质的太赫兹透射光谱按谱线相似程度分为数据集1、数据集2和数据集3;数据集1中物质的光谱图形曲线区分度较高,数据集2区分度较低,数据集3为所有的16种物质集合。从每种物质的太赫兹透射光谱中随机选取100组数据作为训练集,剩余20组数据作为测试集。在每种物质的120个实验数据中,随机选取1个,其中前8种预处理后的数据集1中太赫兹光谱曲线如图1所示,后8种预处理后的数据集2中太赫兹光谱曲线如图2所示。

图15 -Acetylsalicylic Acid等8种物质预处理后的太赫兹透射光谱谱线
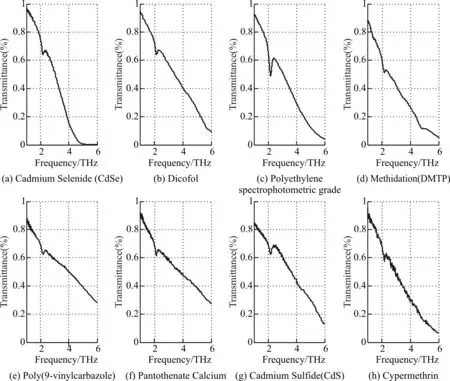
图2 Cadmium Selenide(CdSe)等8种物质预处理后的太赫兹透射光谱谱线
4.2 实验结果及分析
性能评价采用平均查准率均值MAP(Mean Average Precision)和查全率-查准率(Recall-Precision)曲线,查全率和查准率分别定义如下

其中,Nc为检索结果中与查询目标光谱为同种物质的光谱数目,Na为光谱点集中与查询目标光谱为同种物质的全部光谱数目,Nr为检索结果中全部的光谱数目。SAP(Average Precision)为查全率-查准率曲线所包含的面积,MAP为查询光谱的平均SAP值,算法检索出来的相关太赫兹光谱越靠前,MAP越高。
实验中用到的两种对比算法:核化局部敏感哈希算法(Kernelized Locality Sensitive Hashing)[21]和平移不变核化哈希算法(Shift-Invariant Kernel Hashing)[22],这两种算法是基于随机投影的哈希算法中比较有代表性的,都扩展到了核空间而同样在其他领域高维数据中得到了很好的效果。
图3为哈希算法P-stable LSH,KLSH和SIKH在三个数据集的平均准确率的平均值(MAP)示意图。横坐标为哈希编码的长度(code length),纵坐标为MAP值。由图可知,三种哈希算法都可用于太赫兹光谱并可以实现近似最近邻检索。三个基于随机投影的哈希算法(P-stable LSH,KLSH和SIKH)在哈希编码比较短的时候,平均准确率的平均值(MAP)都比较低;当哈希编码的长度增长时,这三种哈希算法的性能都有所提高。P-stable LSH结合了随机投影思想,从概率上保证了光谱数据映射编码前后的相似性一致,在三个数据集中几乎在所有的哈希编码长度下均比其他哈希算法的性能要好,这可以表明,P-stable分布更适用于太赫兹光谱数据。
为了进一步比较三种算法检索太赫兹光谱的性能,分别取哈希编码为48bit和96bit,在三个数据集上的准确率-召回率曲线如图4~图6所示。可以看出,在准确率-召回率评价指标中,基于P-stable的局部敏感哈希所获得的太赫兹光谱哈希编码与其他方法相比,表现出了更好的性能。
表1量化地给出了三种哈希算法在数据集3中的训练时间和测试时间。由表可知,三个基于随机投影的哈希算法(P-stable LSH,KLSH和SIKH)都是非常高效的,特别是P-stable LSH,在训练时间和测试时间上均体现出了很好的性能。就测试时间而言,P-stable LSH是最高效的,因为只需要一个简单的矩阵乘法的操作和一个阈值化处理的过程就可以得到最后的二值哈希编码。
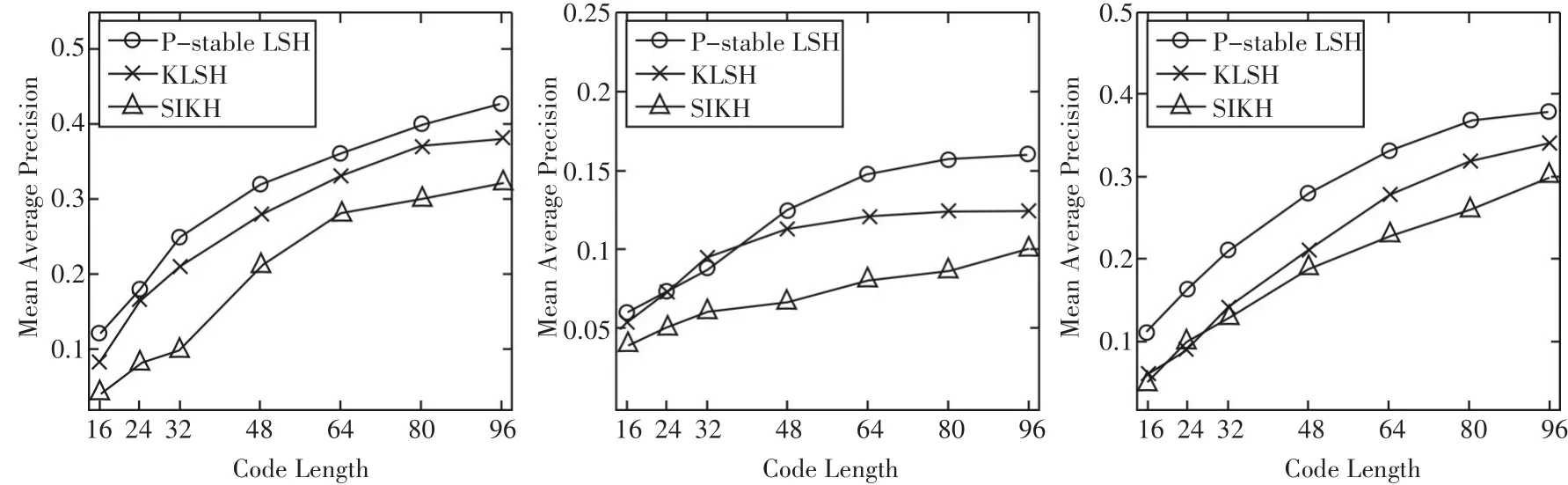
图3 三种参与比较的哈希算法LSH,KLSH和SIKH在三个数据集的平均准确率的平均值(MAP)示意图
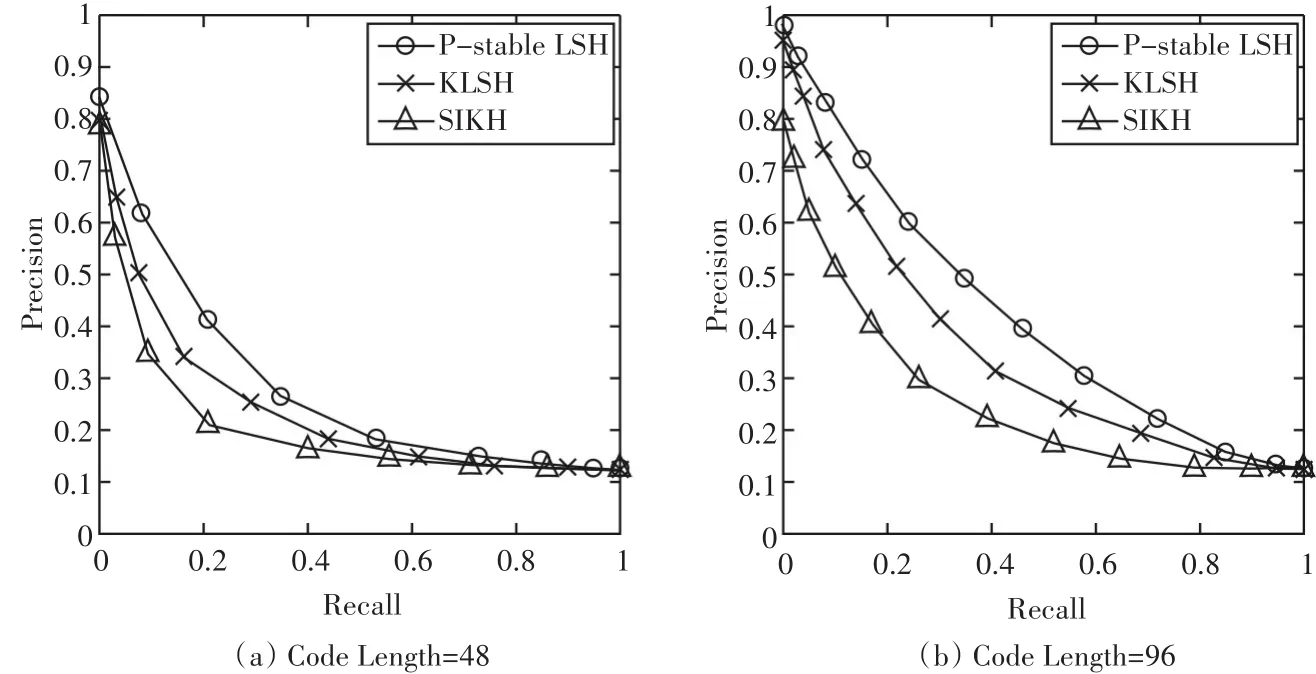
图4 哈希编码分别为48bit和96bit时,各个哈希算法在数据集1中的准确率-召回率曲线示意图。

图5 哈希编码分别为48bit和96bit时,各个哈希算法在数据集2中的准确率-召回率曲线示意图。

图6 哈希编码分别为48bit和96bit时,各个哈希算法在数据集3中的准确率-召回率曲线示意图。

表1 数据集3中三种算法分别在32bit和64bit的训练时间和测试时间
5 结语
本文针对太赫兹光谱近似最近邻检索问题提出了一种基于P-stable分布的局部敏感哈希算法的太赫兹光谱检索方法。该方法可以实现“以谱检谱”的太赫兹光谱检索需求,并能很好地解决效率和准确率问题。实验结果验证了该方法能够有效地对高维太赫兹光谱数据进行降维及二值化编码,并在对比实验中体现了更好的性能。因此该算法在太赫兹光谱检索中是有效且可行的。
[1]Wang G,Wang W N.Experimental and Theoretical Investigations on the Terahertz Vibrational Spectroscopy of Alanine Crystal[J].Acta Physico-Chimica Sinica,2012,28(7):1455-1467.
[2]Parrott E P J,Sun Y,Pickwell-Macpherson E.Terahertz spectroscopy:Its future role in medical diagnoses[J]. Journal of Molecular Structure,2011,1006(1-3):66-76.
[3]Hoshina H,Ishii S,Yamamoto S,et al.Terahertz Spectroscopy in Polymer Research:Assignment of Intermolecular Vibrational Modes and Structural Characterization of Poly(3-Hydroxybutyrate)[J].IEEE Transactions on Terahertz Science&Technology,2013,3(3):248-258.
[4]Zhang W,Nie J,Tu S.Study on identification methods in the detection of transgenic material based on terahertz time domain spectroscopy[J].Optical and Quantum Electronics,2015,47(11):3533-3543.
[5]Chen J,Chen Y,Zhao H,et al.Absorption coefficients of selected explosives and related compounds in the range of 0.1-2.8 THz[J].Optics Express,2007,15(19):12060-12067.
[6]http://webbook.nist.gov/chemistry/thz-ir/
[7]http://www.frascati.enea.it/THZ-BRIDGE/
[8]Notake T,Endo R,Fukunaga K,et al.State-of-the-Art Database of Terahertz Spectroscopy Based on Modern Web Technology[J].Terahertz Science and Technology,IEEE Transactions on,2014,4(1):110-115.
[9]Arya S,Mount DM,Netanyahu N S,et al.An optimal algorithm for approximate nearest neighbor searching fixed dimensions[J].J.ACM,1998,45(6):891-923.
[10]Clarkson K L.An algorithm for approximate closest-point queries[C]//Symposium on Computational Geometry,1994:160-164.
[11]Kleinberg J M.Two algorithms for nearest-neighbor search in high dimensions[C]//STOC,1997:599-608.
[12]Achlioptas D.Database-friendly random projections:Johnson-lindenstrauss with binary coins[J].J.Comput. Syst.Sci.,2003,66(4):671-687.
[13]Datar M,lmmorlica N,Indyk P,et al.Locality"-sensitive hashing scheme based on P-stable distributions[C]//SymposiumonComputationalGeometry2004,2004:253-262.
[14]Ke Y,Sukthankar R,Huston L.An efficient parts-based near-duplicate and sub-image retrieval system[C]// ACM International Conference on Multimedia.ACM,2004:869-876.
[15]Chum O,Philbin J,Isard M,et al.Scalable near identical image and shot detection[C]//ACM International Conference on Image and Video Retrieval.ACM,2007:549-556.
[16]Har-Peled S,Indyk P,Motwani R.Approximate Nearest Neighbor:Towards Removing the Curse of Dimensionality[J].Theory of Computing,2000,604-613(11):604-613.
[17]Gionis A,Indyk P,Motwani R.Similarity Search in High Dimensions via Hashing[C]//International Conference on Very Large Data Bases.Morgan Kaufmann Publishers Inc,2000:518-529.
[18]Charikar M S.Similarity estimation techniques from rounding algorithms[C]//Thiry-Fourth ACM Symposium on Theory of Computing.ACM,2002:380-388.
[19]Indyk P.Stable distributions,pseudo random generators,embeddings and data stream computation[J].Journal of the ACM,2006,53(3):307-323.
[20]Andoni A,Indyk P.Near-Optimal Hashing Algorithms for Approximate Nearest Neighbor in High Dimensions[C]//IEEE Symposium on Foundations of Computer Science.IEEE Computer Society,2006:459-468.
[21]Kulis B,Grauman K.Kernelized locality-sensitive hashing for scalable image search[C]//IEEE,International ConferenceonComputerVision.IEEE,2009:2130-2137.
[22]Raginsky M,Lazebnik S.Locality-sensitive binary codes from shift-invariant kernels[C]//The Neural Information Processing Systems,2009:1509-1517.
Terahertz Spectrum Retrieval Based on P-stable LSH
LI Lingjie1,2SHEN Tao1,2NI Jiapeng1,2
(1.School of Information Engineering and Automation,Kunming University of Science and Technology,Kunming650500)(2.Key Laboratory of Intelligent Information Processing,Kunming University of Science and Technology,Kunming650500)
The nearest neighbor search method of terahertz spectrum is a key problem in the full use of terahertz spectroscopy and related research.At present,there is no THz spectrum database which can provide spectrum search by THz spectrum.Therefore,in this paper,combined with the advantages of hash algorithm based on random projection,a new method of terahertz spectrum retrieval based on P-stable distribution local sensitive hash algorithm is proposed.First of all,through the S-G filter and 3 spline interpolation and resampling,16 kinds of substances were normalized in the terahertz transmission spectrum of 0.9THz~6THz,and then the random projection method P-stable LSH is used to train the above original terahertz spectrum data in high dimension spectrum based on the dimensionality reduction mapping to Hamming space,into the size of only tens of bits hash encoding,finally,parts of the spectrum of each substance selected as a query to retrieve and calculate the Hamming distance of hash code between query point and spectral data database,then the results are sorted and returned.Experimental results show that the retrieval results by locality sensitive hashing algorithm using P-stable is more accurate and more efficient,the mean average precision(MAP)value is higher than other representative hash algorithms based on random projection.
THz spectrum,spectrum retrieval,random projection,P-stable distribution,locality sensitive hashing
TP391
10.3969/j.issn.1672-9722.2017.06.006
2016年12月17日,
2017年1月27日
国家自然科学基金项目(编号:61302042,61671225)资助。
李灵杰,女,硕士研究生,研究方向:太赫兹材料无损检测、机器学习。沈韬,男,博士,教授,博士生导师,研究方向:太赫兹材料无损检测、半导体功能材料、复合材料电学性能。倪家鹏,男,硕士研究生,研究方向:太赫兹材料无损检测、机器学习。

