同步压缩变换及其在机械振动信号处理中的应用

高 威，李 莎

（商丘工学院 机械工程学院，河南 商丘 476000）

同步压缩变换及其在机械振动信号处理中的应用

高 威，李 莎

（商丘工学院 机械工程学院，河南 商丘 476000）

文章将一种音像信号处理方法引入机械运行状态检测领域。首先简介了时频方法的发展史以及同步压缩变换方法（SST）的由来，对基于短时傅里叶变换的SST的算法进行了简要分析，随后重点突出了其在时频图改善与信号分解方面的应用，并用一组变转速下的转子碰磨实验来验证SST其中一个重要用途;最后，总结了SST的优势与不足，并给出了展望。

非平稳信号；同步压缩变换（SST）；时频图改善；信号分解；EMD

针对机械设备的故障检测，传统的诊断技术大多集中在定转速机械设备，但实际上，很多设备在不同的工作要求中其转速是非平稳的，因此，近几年针对非平稳信号的处理方法屡出不穷，时频方法是众多方法中应用最多、最有效的方法之一。时频方法一般可以分为两类，一类是线性的，如短时傅里叶变换（STFT）和小波变换（WT），另一种是在该方法基础上发展起来的时频谱图，即非线性的，如魏格纳分布。

文章将同步压缩变换用于机械振动信号处理领域，并从多个方面与传统的时频方法进行对比，突出该方法的优势。

1 同步压缩变换的原理

同步压缩变换首先是在小波的基础上提出的，然后又用于短时傅里叶变换，文章是基于短时傅里叶变换的同步压缩来进行展开的。

同步压缩变换的思想与合成公式有直接联系：

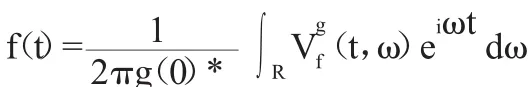
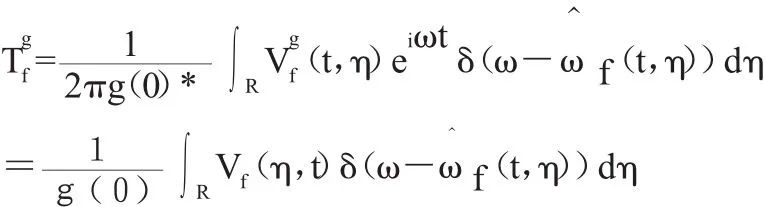
将该公式与时频重分配进行对比，时频重分配是将时频平面上一个局域的能量密度平均值从几何中心重新分配到重心处，可以认为同步压缩变换只是对频率进行了重新分配，因此同步压缩变换可以看做重分配方法的一个特例。

2 同步压缩变换的仿真应用

多成分信号分解。同步压缩变换能够类似EMD对多成分信号进行分解，但又有自身独特的优势。假设多成分信号f=

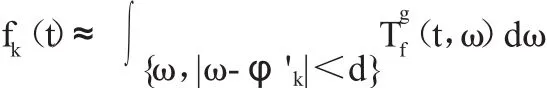
式中d为小参数，由于φ'k在实际中无法直接获得的，但可以通过脊线提取来估计该参数，但基本理论依据都是由Carmona提出的最小化能量函数号可以通过整合相应脊线附近的系数来获得：

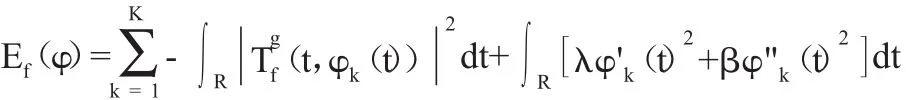
文章使用了一种算法，即各个局部的几何平均算法，该算法简单有效。最后可以用光滑曲线φk来估计φ'k，从而计算单成分信号。故同步压缩变换的分解过程与EMD相反：前者是先通过时频分布得到瞬时频率，最后计算出各模式分量；而后者直接计算出各模式分量，然后获得希尔伯特谱图。

对于双成分信号的分解如图1中所示。由于EMD为纯数据驱动的，无法保证所获得的IMF就是原信号中的某一成分，而同步压缩变换的数学基础是很严密的，它是通过某一成分在时频平面的脊线重构出来的，重构优势明显；并且EMD的分解能力受成分的幅值与频率比值的限制，如若两个成分之间的该值接近，EMD就无法区分出两个模式分量，而对于SST，只要选择合适的窗宽就可以实现较好的识别。

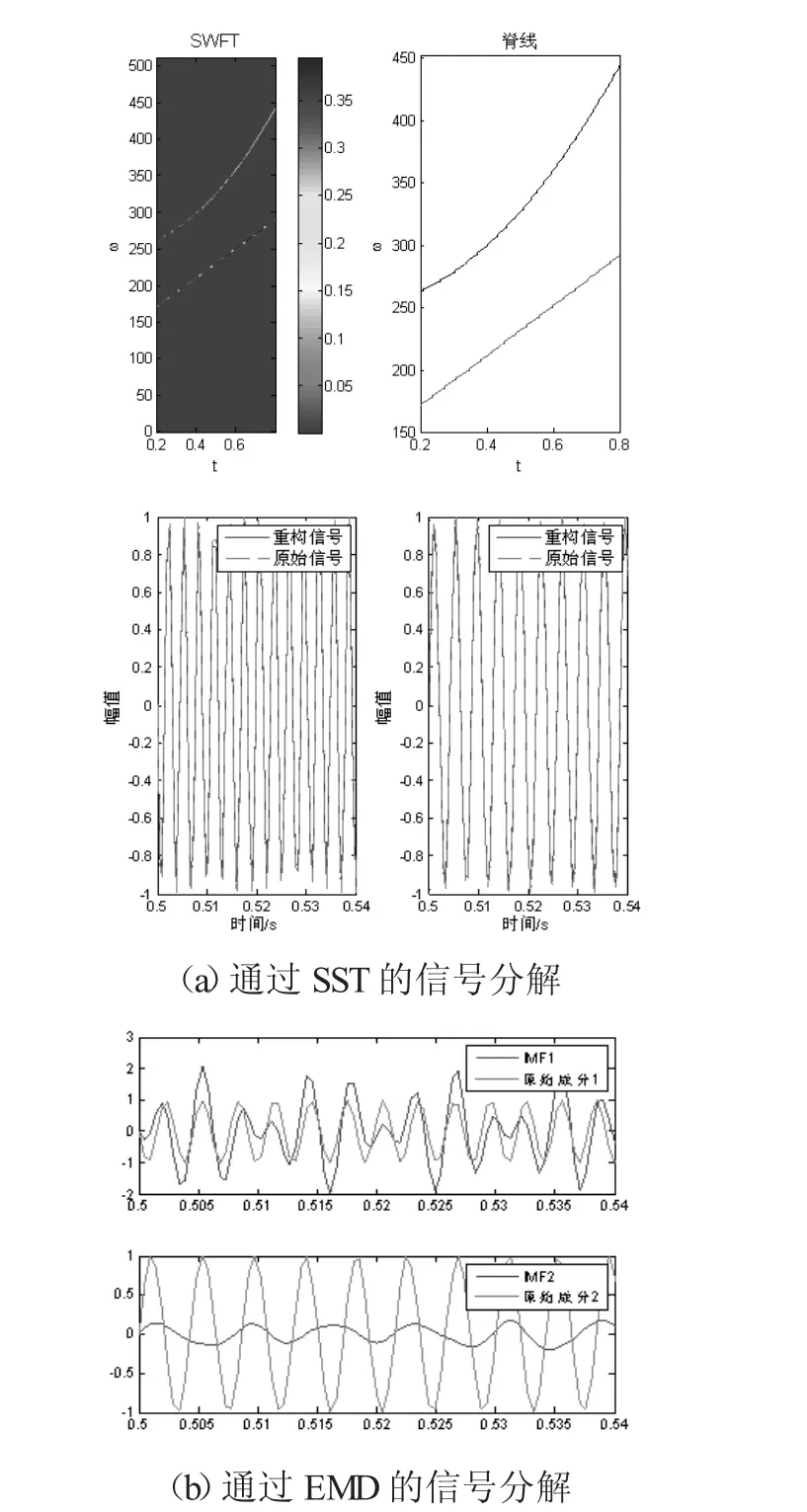
图1 信号分解对比图

3 实验数据处理

用转子试验台模拟动静碰磨故障，转子为匀加速状态，采集振动数据进行分析。分别用短时傅里叶变换和同步压缩变换进行处理实验数据，从中可以看出同步压缩变换相对于传统的时频方法比较清晰，在前四秒同时含有一倍频、二倍频、三倍频等多个倍频分量，这是典型的碰磨故障特征，在四秒之后，由于碰磨区被磨平，碰磨就消失了，因此多倍频相应也消失了。

4 总结展望

同步压缩变换作为一种新的时频分析方法，不仅继承了时频重分配的优势，并且又有自身的优点；文章充分利用了它的优势，可以看出，它可以很好地识别出机械故障。但是该方法在使用中还存在以下缺陷，也即该方法能够进一步完善的地方：①如果要想精确地提取出各个信号成分，必须要首先具备一种检测出模式成分总个数的方法；②文章仿真的是频率调制很弱的信号，如何将该方法用于较高的频率调制信号也应是需要关注的问题；③在实现信号分解，得到的时域信号与原始信号相比有一定的误差，提高该重构精度对于实际工程应用具有很大的价值。

［1］Daubechies I.A nonlinear squeezing of the continuous wavelet transform based on auditory nerve models［J］.Wavelets in Medicine&Biology，1996.

［2］J.Thakur and H.-T.Wu.Synchrosqueezing based recovery of instantaneous frequency from nonuniform samples［J］.SIAM J.Math.Anal，2011，43（5）：2078-2095.

［3］Auger F,Flandrin P.Improving the readability of time-frequency and time-scale representations by the reassignment method［J］.IEEE Transactions on Signal Processing，1995，43（5）：1068-1089.

［4］Daubechies I，Lu J，Wu H T.Synchrosqueezed wavelet transforms：An empirical mode decomposition-like tool［J］.Applied&Computational Harmonic Analysis，2011，30（2）：243-261

Synchronous Compression Transform and Its Application in Mechanical Vibration Signal Processing

GAO Wei，LI Sha
（College of Mechanical Engineering,Shangqiu Institute of Technology，Shangqiu，Henan 476000，China）

This paper introduces a kind of audio and video signal processing method into the field of mechanical running state detection.Firstly，the history of the time-frequency method and the origin of the synchronous compression transformation method （SST）are briefly introduced.The algorithm of SST based on short-time Fourier transform is briefly analyzed，and then it is emphasized that the time-And then use a set of rotor speed grinding experiments to verify SST which is an important use；Finally，it sums up the advantages and disadvantages of SST，and gives a prospect.

non-stationary signal；synchronous compression transform（SST）；time-frequency diagram improvement；signal

TH132.41

A

2095-980X（2017）04-0070-02

2017-03-20

高威，主要研究方向：机械工程。