对称子矩阵约束下矩阵方程AX=B的迭代解法

林 永

宿州学院数学与统计学院，宿州，234000



对称子矩阵约束下矩阵方程AX=B的迭代解法

林 永

宿州学院数学与统计学院，宿州，234000

研究了对称子矩阵约束条件下矩阵方程AX=B的迭代解法。考虑待求矩阵X的特定子矩阵为对称矩阵，利用矩阵分块将AX=B转化为四个低阶矩阵方程构成的方程组，基于残量矩阵极小化原理构造迭代参数，给出了对称子矩阵约束条件下矩阵方程AX=B的一类迭代求解算法。使用该算法，计算过程中可自动判断所求问题的相容性，并在有限的误差范围内迭代出其约束解。数值实验证明了方法的有效性。

矩阵方程；子矩阵约束；迭代法

1 问题的提出

子矩阵约束下矩阵方程的求解问题，是指在限定待求矩阵子矩阵的条件下，对矩阵方程进行求解的问题。文献[1-3]对子矩阵约束下矩阵方程和对称约束问题进行了相关研究，但目前对该类问题采用迭代解法进行研究的文献尚不多见。本文给出了对称子矩阵约束条件下矩阵方程AX=B的一类迭代求解算法，并通过数值实验证明了该方法的有效性。

2 问题的迭代解法

对前述问题，本文基于残量矩阵极小化原理给出如下迭代算法：

(1)输入矩阵A∈Rm×n，B∈Rm×n，X=0∈Rn×n；

(3)计算：

(5)计算：

K=K+1，转(4)。

3 数值实例

本文通过下例证明所构造迭代算法对问题求解的有效性。

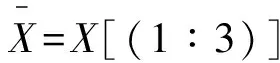
利用本文给出的迭代算法，在Matlab环境下运算，以矩阵的Frobenius范数<10-10作为迭代终止的条件，当迭代次数K=447时，得到满足计算精度要求的解：

该迭代算法的收敛过程如图1所示。

[2]陈世军,张凯院.一类矩阵方程组的对称解及其最佳逼近[J].工程数学学报，2009,26(4):711-715

[3]邹阳芳,周富照,田时宇.实子矩阵约束下矩阵方程AX=B的共轭梯度迭代解法[J].数学理论与应用，2014,34(1):12-17

(责任编辑：汪材印)

10.3969/j.issn.1673-2006.2017.04.027

2017-02-06

安徽省高校自然科学研究重点项目“矩阵方程组一类新的迭代解法及其误差分析研究”(KJ2017A443)。

林永(1975-)，安徽淮北人，博士，副教授，研究方向：矩阵代数及其表示论。

O241.6

A

1673-2006(2017)04-0098-02