基于奇异值形态滤波的核磁测井信号去噪研究
萨其日拉
(东北石油大学 石油工程学院,黑龙江 大庆 163318)
基于奇异值形态滤波的核磁测井信号去噪研究
萨其日拉
(东北石油大学 石油工程学院,黑龙江 大庆 163318)
对于岩性复杂地层条件,核磁共振(NMR)相比其他测井方法能提供更加丰富、有效的地质信息。针对核磁共振测井自旋回波信号带有大量噪声、影响反演计算和地层解释的问题,提出了一种奇异值形态滤波的核磁测井自旋回波信号的去噪新方法,该方法结合奇异值分解(SVD)对随机强噪声滤波效果明显以及形态滤波(MF)可有效抑制脉冲振荡的优点,滤除噪声。实验分析表明: 该方法有效地滤除信号噪声,得到的回波信号反演计算出的T2谱和孔隙度与岩心在实验室条件下测量一致,去噪效果良好。
核磁共振 奇异值分解 形态滤波 自旋回波
核磁共振NMR(nuclear magnetic resonance)测井[1]技术能够提供比常规测井方法更加丰富的地层信息,特别对于复杂岩性、低孔低渗、特殊岩性等世界复杂油气藏的勘探,具有其他测井技术无法比拟的优势。
目前,核磁测井常采用CPMG (carr purcell meiboom gill)方法测量采集到的原始数据为自旋回波串,然而由于实际测量井下环境恶劣, NMR探头同时受到电化学、热力学、重力学、磁场和脉冲激励振荡等作用,尤其在深井中,更有众多的干扰因素,核磁测井所得到的回波信号非常微弱,信噪比极低,因而需要采取有效措施在微弱的回波信号中滤除噪声。
不同于其他微弱信号或已知窄带信号,核磁测井自旋回波信号具有带宽大、信号微弱的特点,检测难度更大。吴磊[2]等人采用小波变换方法对核磁测井信号进行软阈值去噪,一定程度上提高了信噪比,但是选择基小波和小波变换尺度在实际应用中都还是一个难点;蔡剑华[3]等人使用经验模态分解的方法对核磁测井去噪,效果良好,但方法的分解过程依赖数据本身包含的变化信息,容易产生模态混叠和端点效应,影响分解结果。
针对上述问题,本文提出了一种奇异值形态滤波的核磁测井回波信号去噪方法,该方法结合奇异值分解SVD (singular value decomposition)针对随机强噪声滤波效果明显以及形态滤波MF(morphological filter)可有效抑制脉冲振荡的优点,滤除随机噪声信号和局部强干扰噪声,保障后续反演解释处理的准确性。
1 核磁测井信号的数学模型
CPMG核磁测井[4]方法在静磁场中外加脉冲激励,通过NMR探头检测自由进动信号M⊥和自旋回波信号Mz,可表示为
Mz(t)=M0(1-exp(-t/T1))
(1)
M⊥(t)=M⊥maxexp(-t/T2)
(2)
式中:M0——静磁场强度;T1——纵向弛豫时间;T2——横向弛豫时间,T1和T2是描述磁化强度的纵向和横向分量恢复过程的时间常数。
T2[5]是NMR测井中关键的核心部分,通过反演后得到的T2谱可以计算出如岩石孔隙度、孔隙尺寸分布、渗透率、可动流体与束缚流体的饱和度、流体扩散系数、黏度等有关岩石储集层物性及流体特性参数。
由于储层孔隙中存在多种流体组分,所以 CPMG 脉冲序列观测到的自旋回波串是多个单指数衰减叠加在一起的多指数衰减弛豫信号,当把流体组分看成连续的,同时把回波信号作为连续信号时,得到第一类弗雷德霍姆积分方程为
y(t)=∫K(t,T)x(T)dT
(3)
式中:K(t,T)——积分核;T——同横向弛豫时间T2;x(T)——所有流体组分横向弛豫时间曲线,即T2谱,求解积分方程得到x(T)的过程就是反演计算。
2 奇异值分解与形态滤波
2.1 数学形态滤波原理
数学形态学方法对信号波形的研究完全在时域中进行,处理中只取决于信号的局部特征,处理后波形不存在相移和幅值衰减等问题。
数学形态学[6]基本运算包括: 腐蚀、膨胀、开运算和闭运算。设原始信号f(n)为定义在Df=(0, 1, 2, …,N-1)上的离散函数,定义序列结构元素g(n)为Dg=(0, 1, 2, …,M-1)上的离散函数,且N≥M,则f(n)关于g(n)的膨胀运算和腐蚀运算分别为
(f⊕g)(n)=max(f(n-m)+g(m))
(4)
(fΘg)(n)=min(f(n+m)-g(m))
(5)
f(n)关于g(n)的开运算和闭运算分别为
(f∘g)(n)=(fΘg⊕g)(n)
(6)
(f·g)(n)=(f⊕gΘg)(n)
(7)
式中:m∈0, 1, 2, …,M-1;n∈0, 1, 2, …,N-1。
数学形态运算可以有效地抑制、平滑或保留正负脉冲。处理信号时,需要同时消除正、负脉冲干扰,采用开、闭运算的级联形式,构造形态开—闭Foc滤波器和闭—开Fco滤波器,定义为
Foc(f(n))=(f∘g·g)(n)
(8)
Fco(f(n))=(f·g∘g)(n)
(9)
由于开运算的收缩性使得开—闭Foc滤波器输出幅值较小,闭运算的扩张性使得闭—开Fco滤波器的输出幅值较大,这时,需构造1个开—闭Foc和闭—开Fco组合滤波器,定义为
y(n)=[Foc(f(n))+Fco(f(n))]/2
(10)
形态滤波的处理效果不仅取决于所采用的形态算子,还与其结构元素有着密切的关系,当结构元素的形状、尺寸与待处理信号基元相匹配时,滤波效果较好。
在实际工程应用中,由于无法预见待处理信号的数学形态特征,很难确定结构元素类型,常用的方法是将结构元素的灰度值取为零,即扁平形结构元素,避免了对待处理信号的修改,比其他非零结构元素更有效,减少了对信号有用信息的损失。综合考虑,本文选择扁平形结构元素最简单也最有效。
2.2 SVD消噪原理
SVD[7]作为一种数据处理方法已经被成功地运用到信号消噪处理中,是一种较为有效的方法。设信号序列为xl(l=1, 2, 3, …),可构建出阶数为m×n的Hankel矩阵Dm
(11)
Dm做奇异值分解,得到Dm=USV′,其中:U∈Rm × n,V′∈Rm × n,且UU′=I,VV′=I,S是m×n矩阵,对角线元素为λ1, λ2, …, λk, Dm的秩为k,λ1≥λ2≥…≥λk称为Dm的奇异值,U和V分别表示左右奇异阵。
若x为含噪信号,Hankel矩阵Dm定为满秩矩阵,假定Dm的秩为k (k SNR=λ1/λa (12) 式中: SNR——信号信噪比;λa——第a个奇异值。 该种方法在信噪比高时保留奇异值个数多,信噪比低时保留奇异值个数少,奇异值保留个数与信噪比成线性关系。 笔者提出的基于奇异值形态滤波的核磁测井回波信号去噪方法,对于带噪的NMR自旋回波信号,先进行形态滤波,利用形态滤波可有效抑制脉冲振荡的优点,滤除回波信号中的局部脉冲干扰,然后再进行SVD去噪,结合SVD针对随机强噪声滤波的良好效果,滤除回波信号中的随即噪声信号,最后可得到去噪后的自旋回波信号。 为检验奇异值形态滤波去噪效果,模拟带有随机噪声和局部脉冲噪声的信号,模拟信号为f(t)=(1+(10πt))cos(40πt)/30+r(t)+w(i),其中,r(t)是标准差为0.01的白噪声,w(i)为局部脉冲干扰信号。在3.4, 6.8, 10.2, 13.6min有幅值绝对值为0.15的脉冲信号,原始信号与加入噪声后信号如图1所示。 利用式(10)组合滤波器对信号进行消噪处理,得到信号如图2所示。 可以看出,组合形态滤波器对于抑制局部脉冲干扰有良好的效果,随机噪声也有一定消除,但还有很大一部分保留,处理随机噪声效果不显著。 对图1带噪模拟信号进行奇异值分解去噪,得到结果如图3所示。 可以看出,SVD去噪可以有效地去除信号随机干扰部分,但是在3.4, 6.8, 10.2, 13.6min时间点上仍有局部脉冲,处理脉冲干扰能力有限。 图1 加入噪声前后模拟信号的对比 图2 形态滤波对模拟信号消噪效果 图3 奇异值分解去噪结果 采用本文的奇异值形态滤波去噪方法,采用扁平结构形态滤波器滤除脉冲干扰,然后再利用式(12)确定截断奇异值进行分解去噪,最后得到如图4曲线。与原信号相比,该方法能有效去除模拟信号中的随机噪声和局部脉冲噪声,并保留原信号特征。 图4 奇异值形态滤波去噪效果 现场使用MARAN-2 NMR仪测得大庆油田龙 33-23井NMR 数据,得到现场自旋回波数据如图5所示,可以看出现场测量自旋回波信号带有大量噪声,信噪比为15dB。 图5 核磁测井自旋回波信号 使用本文奇异值形态滤波去噪方法对信号进行处理后得到自旋回波信号如图6所示,可以看到信号中噪声已得到有效滤除,去噪后回波信号信噪比提高到29dB。 采用共轭梯度法对去噪后信号进行反演计算,得到T2谱如图7所示。 图6 去噪后自旋回波信号 图7 T2谱图 积分面积即核磁孔隙度Φt: (13) 由T2谱可以得到孔隙度值为17.82%。 实验处理结果与岩心实验室测得的数据吻合,岩心实验室测得孔隙度为17.96%,表明本文方法对于去除核磁共振中的强噪声作用明显有效。 对于NMR测井自旋回波信号带有大量噪声的问题,笔者将SVD和MF算法有机结合应用到核磁回波信号去噪处理中。实验表明: 该方法能有效去除强噪声对信号的作用,实际测井数据信噪比由15dB提高到29dB,基于去噪后的数据孔隙度计算和反演T2谱,与实验岩心测量结果基本一致。 [1] 程晶晶.多频NMR测井系统中微弱信号检测问题研究[D].武汉: 华中科技大学, 2011. [2] 吴磊,孔力,程晶晶.基于小波变换的核磁共振测井信号去噪算法设计[J]. 仪表技术与传感器, 2011 (10): 71-72. [3] 蔡剑华,汤井田,胡惟文.基于经验模态分解的核磁共振测井信号去噪新方法[J]. 核电子学与探测技术, 2010, 30(03): 390-393. [4] 李鹏举.核磁共振T2谱反演及流体识别评价方法研究[D].大庆: 东北石油大学, 2010. [5] 彭石林.核磁共振技术在石油分析和探测中的应用[D].武汉: 中国科学院研究生院 (武汉物理与数学研究所), 2006. [6] 刘俊峰, 邓居智, 陈辉, 等. 基于多结构元素形态滤波的大地电磁去噪[J]. 物探与化探, 2014, 38(01): 109-114. [7] 王太勇,王正英,胥永刚,等.基于SVD降噪的经验模式分解及其工程应用[J].振动与冲击,2005,24(04): 96-98. [8] 迟唤昭, 刘财,单玄龙.谱反演方法在致密薄层砂体预测中的应用研究[J].石油物探,2015, 54(03): 337-344. [9] 朱建华. 核磁测井在海拉尔地区储层分类中的应用[J]. 大庆石油地质与开发, 2008, 27(03): 136-138. Research on De-noising of Nuclear Magnetic Logging Signal Based on Singular Value Morphological Filter Sachsla (College of Petroleum Engineering, Northeast Petroleum University, Daqing, 163318, China) s: For lithologic complex geological conditions, richer and more effective geological information can be provided with nuclear magnetic resonance (NMR) comparing to other logging methods. Aiming at problems of lots of noise, impact on inversion calculation and follow-up stratigraphic interpretation of NMR spin echo signal, a novel de-noising method of singular value morphological filter is proposed. It combines advantages of singular value decomposition (SVD) with obvious random noise filtration and morphological filter (MF) with effective pulse oscillation inhibition to filter out noise. Experimental analysis indicates signal noise can be filtered out with above methods.T2 spectrum and porosity with inverse computation from consequence obtained echo signal is in conformity with result which is measured under laboratory conditions. The effect of de-noising is obvious. nuclear magnetic resonance; singular value decomposition; morphological filter; spin echo 萨其日拉(1994—),男,蒙古族人,现就职于东北石油大学石油工程学院,主要从事测井技术研究工作。 TP273 B 1007-7324(2017)02-0042-04 稿件收到日期: 2016-08-18,修改稿收到日期: 2016-12-20。3 奇异值形态滤波去噪方法


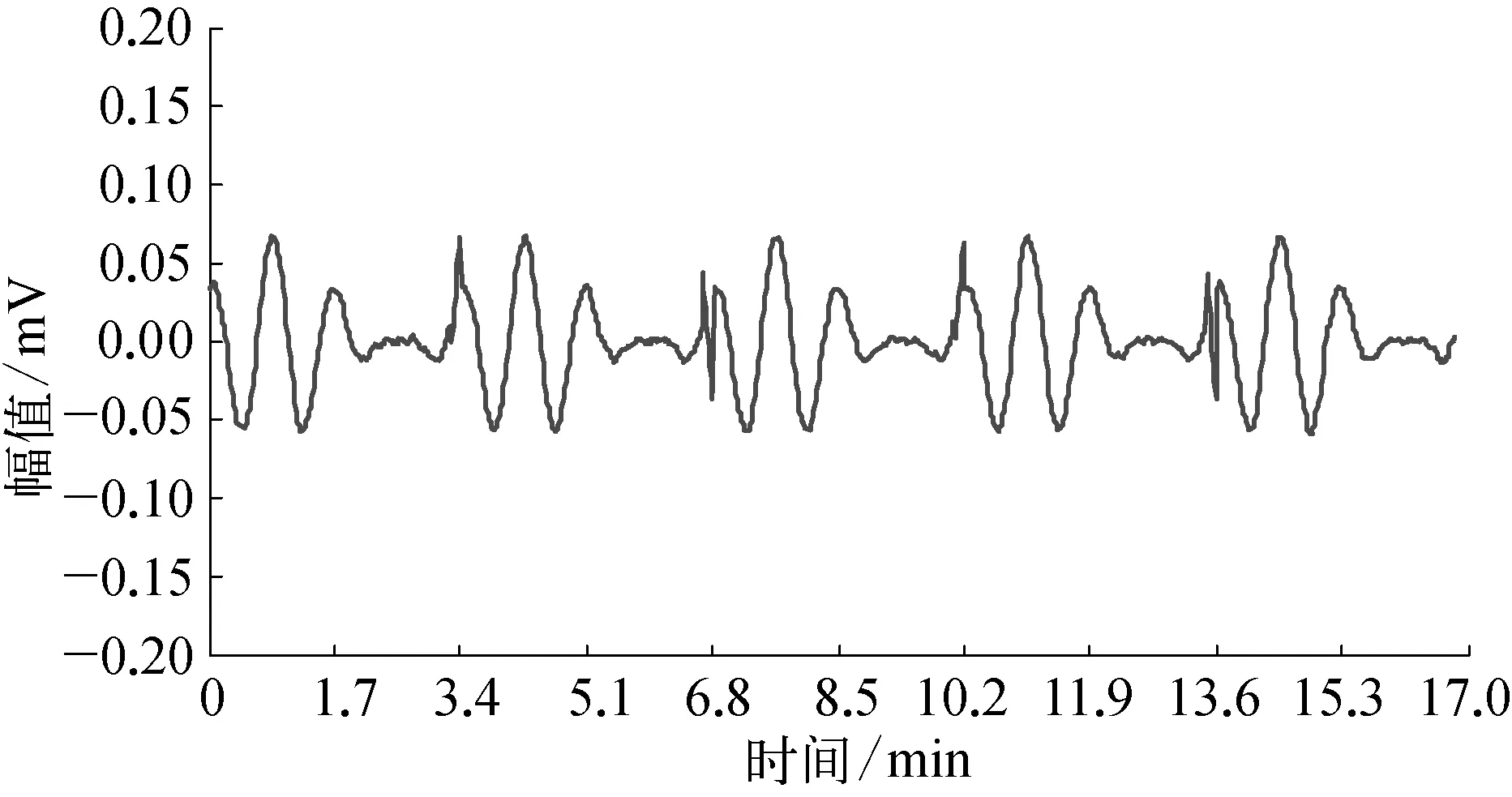
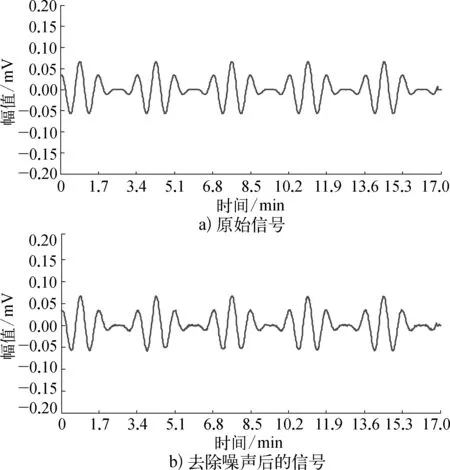
4 应用实例


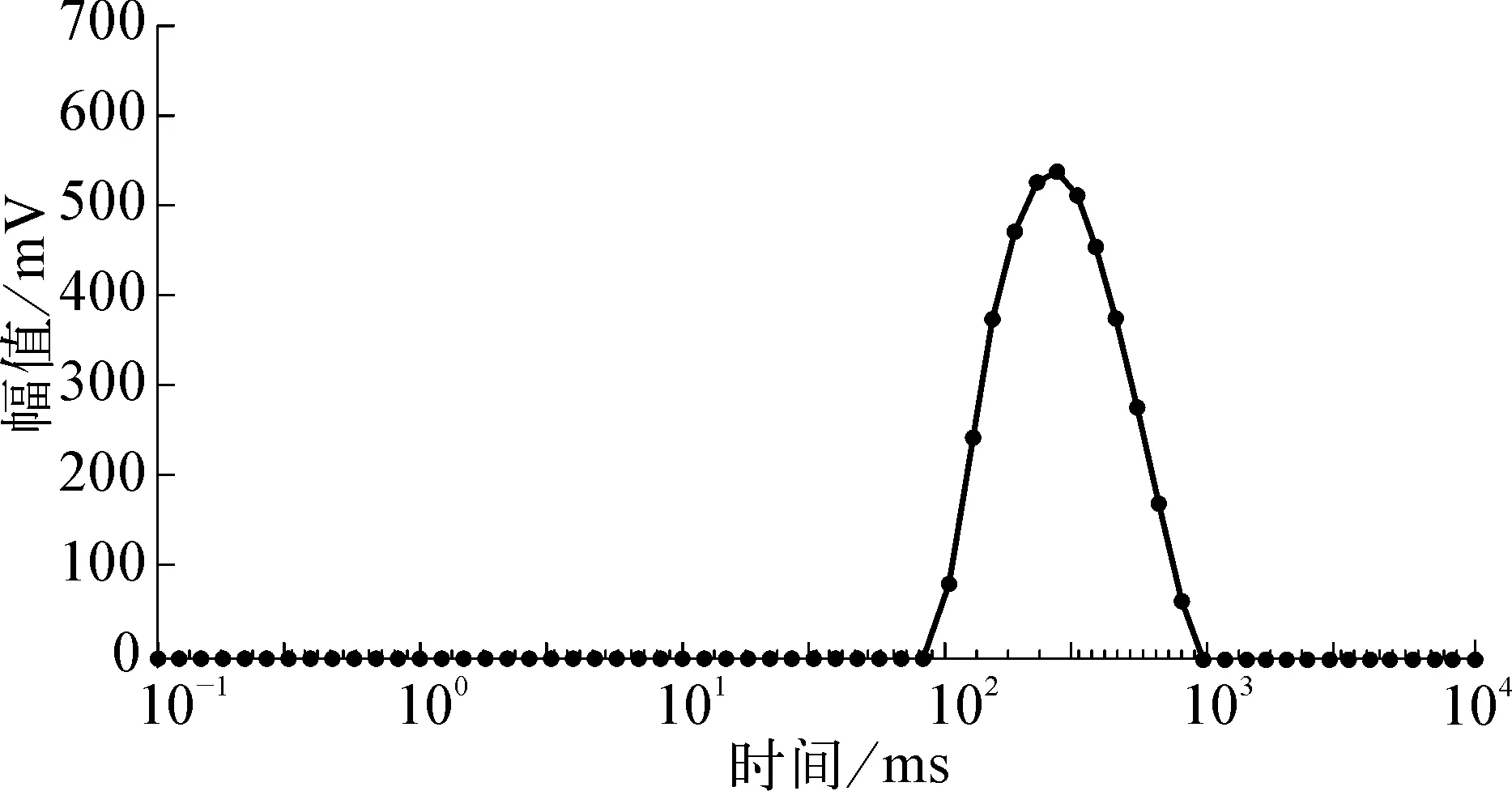
5 结 论

