基于显露子串挖掘的基因序列模体识别算法

张懿璞+闫茂德++侯俊++阚丹会

摘 要： 染色质免疫共沉淀技术将模体识别问题拓展到了全基因组范围，但因数据量过大，传统的模体识别算法往往运算过慢从而无法很好地解决此问题。为了解决传统算法的缺点，提出一种用于ChIP?seq数据的替换显露子串寻找问题的算法FastESE，通过测试集和控制集的比对找出显露子串并搜索其（l，d）替换实例组成相应的位置概率矩阵，再使用权重信息量对这些子串进行聚类，最终找出集合中的替换显露子串。使用真实的ChIP?seq数据对该研究算法进行有效性验证，实验结果表明，FastESE可以在合理时间内有效解决ChIP?seq中的模体识别问题。

关键词： 染色质免疫共沉淀； 显露子串； 模体识别； FastESE

中圖分类号： TN911?34； TP301.6 文献标识码： A 文章编号： 1004?373X（2017）12?0006?05

Abstract： Recently， the development of chromatin immunoprecipitation technique has extended the motif identification problem to the genome?wide range， but the traditional motif identification algorithms runs too slowly and hard to solve this large?scale data problem. In order to solve the shortcomings of the traditional algorithms， a substituted emerging substring search algorithm named FastESE applied to ChIP?seq data is proposed in this research. The emerging substrings are found out by comparing the test dataset and the control dataset， and then its substituted instances are searched to constitute the corresponding position probabilistic matrix. The weighted information content is adopted to cluster these substrings， and Finally， discover the substituted emerging substrings. The effectiveness of proposed algorithm was verified with the real ChIP?seq data. The experimental results show that the FastESE can deal with the motif identification problem in the ChIP?seq data in a proper time.

Keywords： chromatin immunoprecipitation； emerging substring； motif identification； FastESE

0 引 言

模体识别问题是研究基因序列的一个重要并且有挑战性的问题，一直以来受到计算机学家和生物学家的重点研究。随着染色质免疫共沉淀技术（Chromatin Immunoprecipitation，ChIP）的发展[1?2]，染色质免疫共沉淀技术与高通量测序方法结合的ChIP?seq技术将模体识别问题拓展到了全基因组范围。而这类ChIP?seq数据量比起传统的模体识别数据，数据规模大大增加[3]，这也就使得传统的模体识别算法难以很好地解决ChIP?seq数据的模体识别问题[4]。

近些年，一些传统算法也提出了用于ChIP数据的版本，如HMS，STEME，Weeder[5?7]等。这些算法可以解决部分ChIP?seq模体识别问题，但仍存在不足，例如HMS在训练时只能使用部分得分较高的序列；而STEME使用后缀树加速了期望最大化求精，但只能用于寻找较短的模体；Weeder只能将单个模体作为每次运行的输出结果，不符合实际需求。

针对ChIP?seq数据含有序列条数较多（上千条），但长度相对较短的特征（通常为几百个碱基）。一些研究者将模体识别问题转化为替换显露子串挖掘问题[8]（Substituted emerging substrings mining problem），即从背景成分较少，相对较为干净的大量序列中，区分出一些具有显著性特征的子串。

本文中，针对上述ChIP数据的特点和传统模体识别算法存在的缺陷，提出一种新的算法FastSES（Fast Substituted Emerging Substrings finding algorithm），用于ChIP?seq数据中替换显露子串的搜索，FastSES通过含有显露子串的测试集和不含显露子串的控制集进行比对，筛选出频率较高的显露子串并生成对应的概率分布矩阵，再对其进行聚类寻找最终的替换显露子串。使用老鼠胚胎干细胞上的多组ChIP?seq数据对本文算法进行测试，实验结果表明本文算法可以在合理时间内有效找出ChIP?seq序列中的模体。

1 相关工作

1.1 问题定义

令Σ={k1，k2，…，km}为序列生成所使用的字母表，由Σ生成的序列集合S={S1，S2，…，St}，集合S中任一序列Si=，其长度均为n（s∈Σ）。已知长度为l的子串A=与长度为n的序列S=，如果对于，都有=，那么A就为S的一个子串，记为。如果A≠S，记为。

（1） 显露子串挖掘问题（Emerging substrings mining problem）。已知由字符集Σ生成的测试序列集合St和控制序列集合Sc，令λf为频率阈值，λg （λg>1）为增长率阈值。则对于一个输入集合中的子串u，当f（u，St）≥λf并且g（u，St，Sc）≥λg时，称该字符串为一个显露子串。这里f（u，S）表示子串u在集合S中发生的频率，表示子串u在测试集合St中相对于控制集合Sc的增长率。g（u，St，Sc）的值越大，子串u在两个集合中的相对分辨度就越高。显露子串挖掘问题就是通过搜索序列集合中的每一个子串，寻找那些同时满足f（u，St）≥λf和g（u，St，Sc）≥λg的子串。

（2） 替换显露子串挖掘问题（Substituted emerging substrings mining problem）。对一个由字符集Σ生成的长度为l的字符串u，如果存在与其长度相同的子串u′，u′与u在至多d（d

1.2 数学模型

显露子串通常可以用fwk表示字符k出现在子串第w个位置的频率，f0k为背景成分中出现字符k的概率。对于序列中任一长度为l的子串A=，第w个位置字符aw的对数似然值即为：

为了更好地表示显露子串，在传统的模体成分和背景成分之外还考虑到各位置间的内在依赖关系，也就是某些连续字符组合的频率脱离了独立模体分布的期望概率[9]。如在连续位置出现的字符“AC”的概率与第一个位置出现字符“A”，第二个位置出现字符“C”的联合概率有明显的差异，即认为这两个位置存在内在依赖关系。令Φw，w+1表示子串内第w和第w+1个位置出现字符aw，aw+1的内在依赖概率，其对数似然值为：

式中，Φ0表示背景概率。由式（2）可计算子串x的对数似然比（Log?Likelihood Ratio，LLR）：

式（4）为x各位置字符独立时的概率，而式（5）为x各位置字符考虑内在依赖关系时的概率。

2 算法描述

对于ChIP?seq数据中的替换显露子串挖掘问题，采用差异模体发现方法，也就是输入含有替换显露子串的测试集和不含替换显露子串的控制集两个集合，首先找到显露子串问题，再对替换子串进行拓展聚类，寻找相应的替换显露子串。通常，在ChIP?seq数据中，测试集是ChIP?seq的峰值区域，控制集可以是非峰值区域或者不同ChIP?seq数据中的类似序列。基于上述方法，FastESE算法由词频分析、位置频率矩阵构建、聚类三个阶段构成。

2.1 詞频统计

对于长度为l的子串（l?mer），其在数据集中可能出现的种类有4l个，那么首先在4l个子串中搜索显露子串，即在测试集中频繁出现而在控制集中很少出现的那些子串。

令S1表示输入的测试集，通常为含有模体的ChIP数据；S2为控制集，通常使用不含模体的背景序列作为参照。由于显露子串长度l未知，一般的，选取长度范围为6～12的子串，统计其相应数量并将每一个固定长度的子串存储在O（4l）的空间中。为了方便理解，在表1中举例表示对每一个l?mer计数并搜索显露子串。对于同时满足f（u，St）>λf和g（u，St，Sc）>λg的子串，如“TCTGAG”，即为显露子串。

如果输入的测试集和控制集均含有长度为n的t条序列，那么进行词频统计寻找显露子串的计算复杂度仅为O（ntl），这仅与传统训练方法中一次迭代的计算量相同。通过本步骤，可以快速地移除背景成分的干扰，大大降低运算量。

表1 显露子串搜索样例

2.2 构建位置频率矩阵

由于显露子串只是对子串进行的基于字符的一致序列描述，并无法反映其统计显著性。需要生成其相应的位置频率矩阵，从而进一步地衡量其统计显著性。在本步骤中，通过搜索每一个显露子串的替换（l，d）实例并计算每个替换实例的z值进行筛选，从而生成对应的位置频率矩阵。这里使用的z值是基于超几何概率分布（Hyper?geometric Probability Distribution）的估计得到[10]：

式中：A1和A2分别表示某一个子串在集合S1和S2中出现的数量；C1和C2分别表示集合S1和S2中子串的总数量；。同样通过表2来举例说明位置频率矩阵生成的过程。

在表2中，显露子串“ACCACGTG”在S1和S2中分别出现119次和9次，已知l=8，选取d=1，即（l，d）=（8，1），在24个替换子串中筛选显露子串“ACCACGTG”的显露替换子串。接下来，分别计算24个替换子串的z值，并选择z>1.643的子串为合格的显露替换子串（如替换子串的z值都小于1.643，取z值为正即可）。将合格的显露替换子串与显露子串在测试集和控制集中每个位置上出现字符的数量相加，即可得到显露子串在测试集和控制集中对应的位置计数矩阵N1，N2。注意到，由于测试集和控制集的大小不同，那么控制集中子串的数量需要使用进行调整；并且，比起初始的搜索空间4l = 65 536，使用（l，d）进行替换子串的搜索可以使得计算量大大降低。

考虑到测试集中包含有所要寻找的显露子串和背景序列，而控制集是完全由背景序列构成，那么为了最大限度地消除测试集中显露子串受到背景序列的干扰，使用控制集对测试集的预测结果进行纠正。也就是，将N2看作是N1中背景序列的期望计数矩阵，则所要寻找的显露子串的位置计数矩阵N=max（N1-N2，0）。在N中的每个位置，还加入1%的伪计数防止零概率的出现，通过N即可得到显露子串的概率分布与字符的内在依赖关系分布。

2.3 聚 类

由各显露子串的概率分布，就可以通过计算对数似然比（LLR）来评价其显著性，见式（3）。而针对那些较为相近的显露子串，使用基于LLC的WIC值（Weighted Information Content）来度量子串间的相似度[11]。WIC由子串α和子串β定义为：

（7）

式中：δ表示模体α的第δ个位置；ψ为模体β的第ψ个位置；ξ一般取值[11]为2.5；LLC（αδ）表示模体α第δ个位置的对数似然值；DIC（Differential Information Content）表示信息量差异，定义如下：

（8）

当一个新的显露子串被找到时，首先根据式（7）计算WIC值来检查是否有已预测出的相似显露子串，如果有，比较其LLR，保留LLR高的；如果没有，用新显露子串代替原显露子串中LLR最小的，如此进行直至没有新显露子串被发现。FastESE算法流程如下：

输入：测试集S1控制集S2

输出：模体集C

For l ← lmin to lmax do

For each l?mer of 4l l?mers： u do

if f（u，St）≥λf && g（u，St，Sc）≥λg then

add u to Xs

For each l?mer of Xs：x do

For each d ← 1 to dmax do

calculate z?score of each neighborhood instance x′

if z（x′）>1.643 then

Add x′ to Xq

use x and Xq to construct Θ and Φ

add Θ to set A and add Φ to set B

For each Θ of A do

use Θ and corresponding Φ to compute LLC and WIC.

add xmotif formed by Θ of top LLR score to C

return C

其中，第1～4行为词频统计，寻找显露子串的过程；第5～11行为通过显露子串，生成其相应位置频率矩阵的过程；第12～15行为聚类并输出最终结果。

3 实验分析

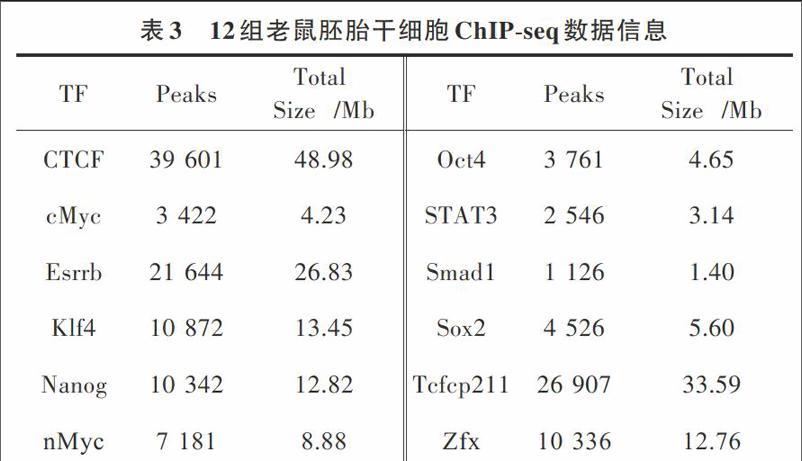
为了测试本文算法性能，在此选择了12组具有物种多样性特征的老鼠胚胎干细胞（mES cells）ChIP?seq数据[12]，具体信息如表3所示。

其中Nanog，Oct4，Sox2，Esrrb和Zfx为自我复制的调控区域提取出的数据；Tcfcp2l1是胚胎干细胞中的优先调控区域提出的数据；Klf4，cMyc，nMyc是重组因子数据；Smad1和STAT3对信号通路有着重要意义；而CTCF是转录隔离的重要成分。通过这些老鼠胚胎干细胞的ChIP?seq数据，选取峰值为中心，左右各100bp的序列片段为测试集，而在测试集序列两端向外再延伸400bp后，选取长度500bp的序列片段作为控制集合。

FastESE算法运行参数设置如下：子串搜索长度范围为6～12，当每条序列中含有一个替换显露子串时λf=0.8Pocc；当每条序列中含有一个或不含替换显露子串时λf=0.6Pocc；当每条序列中含有零个或多个替换显露子串时λf=1.2Pocc。Pocc=0.2，0.5，0.8分别表示高保守性、中保守性和低保守性，λg=2。搜索替换显露子串的（l，d）包括（6，1），（7，1），（8，1），（9，2），（10，2），（11，2）和（12，3）。z=1.643为默认阈值。使用Matlab语言在Windows系统环境下实现FastESE算法，测试运行环境为2.67 Hz CPU和4 GB内存。

为了更好地显示算法性能，使用Chen等人使用的WEEDER算法所公布的模体与本文方法进行比较。为了掌握预测模体和所公布数据间的相似性[13]，采用将统计显著性表现为LOGO图的方式，这也是现在被广为使用的一种对比方式。图1为算法发现的主要模体和Chen公布模体的对比，可以看到本文的算法可以有效地寻找到这些真实数据中的主要模体，LOGO图显示了较好的准确率。

FastESE预测的模体LOGO图

除准确性外，还与现在流行的模体识别算法在时间效率上进行了比较，见图2。

从图2的结果可以看到，本文算法比起Weeder，HMS和ChIPMunk等流行算法，具有更好的效率，在处理更大规模的基因序列时所用时间最短。与FastESE相比，Weeder算法在设计时只是针对传统模体识别问题，所以在处理上千条序列的数据时效率很低；而HMS在处理ChIP数据时只是选取部分序列进行模体识别，不能完全处理全部的数据，这样就導致处理大规模序列时训练时间较长、迭代缓慢，从而影响效率；ChIPMunk同样也存在收敛缓慢、训练时间较长的缺点。而本文算法在处理上百兆数据时，仅需要几分钟，如在处理Sox2数据时，如果取（l，d）=（8，1），本文算法需要536 s，而（l，d）=（10，1）时，需运行620 s。

此外，将Nanog与Sox2或Oct4数据集对比，还使用FastESE算法找出了部分显著性较弱的复合模体。将Nanog的数据作为测试集，Sox2或Oct4数据作为控制集作为输入，Nanog VS Oct4的结果为“GCAATCAA”，Nanog VS Sox2的结果则为“CCATCAA”。也就是说，在这个相似区域中，Nanog模体与Sox2和Oct4转录因子中的一个或两个间接绑定。这些显著性较弱的复合模体与Chen等人公布的Sox2和Oct4数据中有相似的结合区域相吻合，证明了本文算法在寻找多个模体时仍具有较好的性能。

4 结 语

本文提出一种用于大规模ChIP?seq数据的替换显露子串寻找问题的算法FastESE，通过测试集和控制集的比对找出出现频率相对较高的子串，进一步搜索其（l，d）替换实例并进行聚类，筛选出具有较高信息量的子串即为替换显露子串。使用老鼠胚胎干细胞的ChIP?seq数据进行实验证明，FastESE可以在合理时间内有效寻找到大规模ChIP?seq序列中的替换显露子串。但是，在基因序列中这些替换显露子串，即特殊的结合位点，往往具有不同功能，其功能性还需要进一步的实验进行验证。同时，在复杂的基因调控区域中具有特殊结构与功能的显露子串也是今后研究的重点之一。

参考文献

[1] MARDIS E R. ChIP?seq： welcome to the new frontier [J]. Nat methods， 2007， 4（8）： 613?617.

[2] JIC C， CARSON MB， WANG Y， et al. A new exhaustive method and strategy for finding motifs in ChIP?enriched regions [J]. Plos one， 2014， 9（1）： e86044.

[3] JOHNSON D S. Genome?wide mapping of in vivo protein?DNA interactions [J]. Science， 2007， 316（5830）： 1497?1502.

[4] ZAMBELLI F， PESOLE G. Motif discovery and transcription factor binding sites before and after the next?generation sequencing era [J]. Briefings in bioinformatics， 2013， 14（2）： 225?237.

[5] PAVESI G， MAURI G. An algorithm for finding signals of unknown length in DNA sequences [J]. Bioinformatics， 2001， 17（Suppl 1）： S207?S214.

[6] HU M. On the detection and refinement of transcription factor binding sites using ChIP?Seq data [J]. Nucleic acids research， 2010， 38（7）： 2154?2167.

[7] REID J E， WERNISCH L. STEME： efficient em to find motifs in large data sets [J]. Nucleic acids research， 2011， 39（18）： 126?131.

[8] FISCHER J， HEUN V. Optimal string mining under frequency constraints， in knowledge discovery in databases [C]// Proceedings of 2006 PKDD. Heidelberg， Berlin： Springer， 2006：139?150.

[9] BULYK M L， JOHNSON P L. Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors [J]. Nucleic acids research， 2002， 30（5）： 1255?1261.

[10] SHAROV A A， Ko M S H. Exhaustive search for over?represented DNA sequence motifs with CisFinder [J]. DNA research， 2009， 16（5）： 261?273.

[11] VAN HEERINGEN S J， VEENSTRA G J C. Gimme motifs： a Denovo motif prediction pipeline for ChIP?sequencing experiments [J]. Bioinformatics， 2011， 27（2）： 270?271.

[12] YU Q. An efficient algorithm for discovering motifs in large DNA data sets [J]. IEEE transactions on nanobioscience， 2015， 14（5）： 535?44.

[13] THOMAS?CHOLLIER M. RSAT peak?motifs： motif analysis in full?size ChIP?seq datasets [J]. Nucleic acids research， 2012， 40（4）： e31?e31.

[14] SUN C， HUO H， YU Q， et al. An affinity propagation?based DNA motif discovery algorithm [J]. Biomed research international， 2015， 2015： 853461.