钢管混凝土拱桥使用阶段受力特性分析

周金枝， 谢 瑛， 江 淦

(1 湖北工业大学土木工程与建筑学院， 湖北 武汉 430068； 2 中铁大桥科学研究院有限公司， 湖北 武汉 430034)

钢管混凝土拱桥使用阶段受力特性分析

周金枝1， 谢 瑛1， 江 淦2

(1 湖北工业大学土木工程与建筑学院， 湖北 武汉 430068； 2 中铁大桥科学研究院有限公司， 湖北 武汉 430034)

对钢管混凝土拱桥理论计算中的刚度取值进行了讨论，对拱桥在正常使用极限状态下的静力和动力特性分析进行了阐述，以郧县汉江二桥为例，应用有限元的方法对中承式拱桥使用阶段的受力特性进行了计算分析，并运用荷载试验的方法进行验证。

钢管混凝土拱桥; 刚度；静力特性；动力特性

中承式钢管混凝土系杆拱桥由于跨越能力强、适应地域广、造型优美、承载能力高、施工简便等优点[1]，近年来得到了广泛的发展。该桥型利用了钢管和混凝土两种材料在受力过程中相互间的组合作用，充分发挥两种材料的优点，使其具有优越的力学性能。本文以郧县汉江二桥为背景，介绍中承式钢管混凝土拱桥使用阶段的受力特点及分析方法，并运用荷载试验的方法进行验证。

1 钢管混凝土拱桥受力特性分析

钢管混凝土拱桥由于采用了钢和混凝土两种材料，其截面刚度的取值与其他拱桥相比有着很大的不同，结构的应力、挠度、稳定性和动力性能计算结果的准确性都与合理选择截面刚度密切相关。本文首先讨论钢管混凝土拱桥截面刚度的取值方法，再对结构正常使用极限状态下的静力和动力计算做一阐述。

1.1 刚度取值

钢管混凝土拱桥截面刚度计算常用的方法有：截面折算法、刚度累加法、统一理论法。

1.1.1 截面折算法 截面折算法是基于刚度等效原则，将钢材和混凝土两种材料等效简化为两者之中的其中一种[2]，例如全部等效为钢材，主要计算公式如下：

A=As+nAc

I=Is+nIc

n=EC/ES

式中：A、I为钢管混凝土组合截面的截面面积和截面惯性矩，As、Is、Es为钢管的截面面积、截面惯性矩和弹性模量，Ac、Ic、Es为钢管内混凝土的截面面积、截面惯性矩和弹性模量。

1.1.2 刚度累加法 刚度累加法是将钢材和混凝土两种材料的刚度进行叠加，该理论认为在弹性工作阶段，钢管和混凝土两种材料均单独发挥作用[3]，《钢管混凝土结构设计与施工规程》(CECS28：90)即采用此方法计算截面刚度，其计算公式如下：

EA=ESAS+ECAc

EI=ESIS+ECIc

式中符号意义同前。

1.1.3 统一理论法 该方法认为钢管混凝土中的钢材和混凝土可视作一种复合材料，通过大量试验，建立起该复合材料的应力-应变曲线(即本构关系)，通过数值分析计算，得到钢管混凝土的组合弹性轴压模量Esc，通过几何计算得到组合截面面积ASC、组合截面惯性矩ISC。《公路钢管混凝土拱桥设计规范》(JTG D65-06-2015)即采用此方法计算截面刚度。图1为钢管混凝土本构关系。本桥的计算中也采用了统一理论法对截面刚度进行计算。

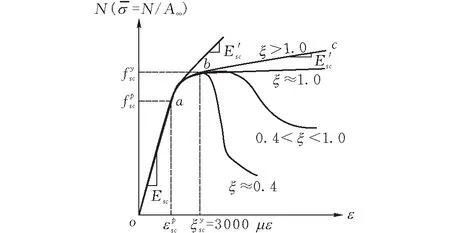
图 1 钢管混凝土本构关系

1.2 静力特性分析

求解钢管混凝土拱桥在使用阶段的内力和挠度，主要依据线弹性理论按结构力学的一般方法。对于桁架拱，其截面组合内力及应力按下列公式进行计算，内力计算参数见图2。

对于钢管混凝土桥梁，其在活载作用下的挠度一般会设置限值，以保证良好的竖向刚度。

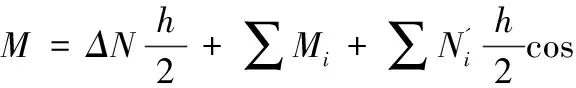
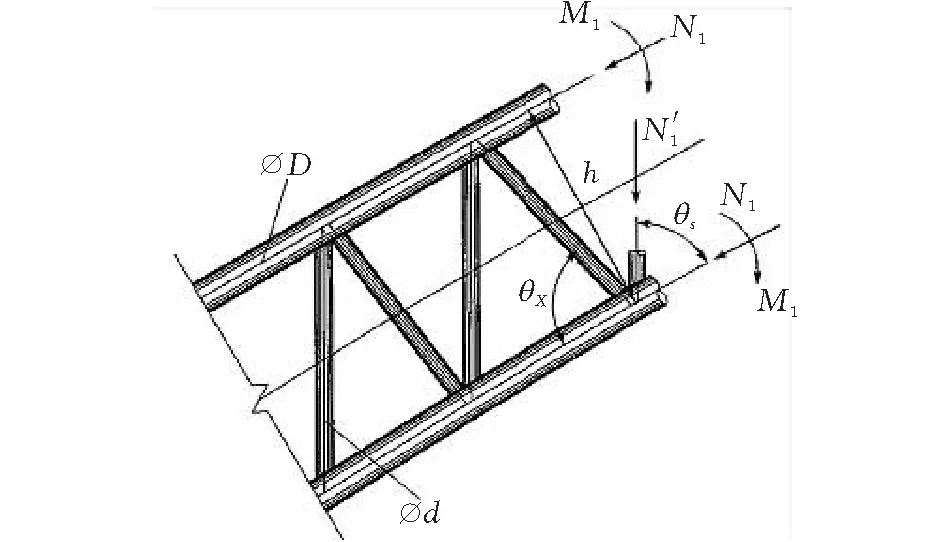
图 2 内力计算参数

1.3 动力特性分析

桥梁动力特性参数主要是指结构的自振频率、振型、阻尼比等。在动力学计算过程中，根据结构的动力学基本平衡方程：

可推导出结构自振特性的有限元计算公式如下：

K-ω2M{φ}=0

采用子空间迭代法求解上式，得到的ωi和φi即是桥梁结构的第n阶频率和对应振型。

2 工程背景

郧县汉江二桥跨径为65 m+200 m+65 m，矢跨比1/4.44，拱轴系数m=1.6，主跨为钢管混凝拱，边跨为混凝土拱。主拱圈为桁式拱圈，每片拱圈由4根φ900mm×18mm的钢管组成。拱圈宽2.60m，高4.2m，两圈中心距为19.0m，拱肋内灌注C50混凝土，拱肋间共设置7道横撑。边拱矢跨比为1/3.42，拱轴系数m=1.6，截面形式为矩形截面，宽3.50 m，高4.00 m，两圈间设置2组横撑。全桥共20束系杆。全桥总体布置如图3，主拱拱圈截面见图4。

图 3 桥梁总体布置

图 4 钢管拱肋截面

3 有限元分析

采用桥梁专用空间有限元分析软件MIDAS/ CIVIL 2012建立空间三维模型。其中边跨混凝土拱肋、主跨拱肋、横梁、横撑采用梁单元建模，系杆和吊杆采用桁架单元建模。边跨混凝土梁和主跨组合梁的牛腿构造，在建模时采用共节点形式，但释放该节点处的梁端转角和纵向位移，拱座底部基础采用桩底固接，拱肋与承台刚接，两个边墩处约束主梁竖向位移。计算模型共包括2779个空间单元，1999个节点。

桥梁技术标准：双向四车道，设计荷载为城市—A级。车道横向折减系数0.67；车道冲击系数μ为0.1；人群荷载为3.0kN/m2。有限元模型见图5。

图 5 有限元模型

4 静力试验结果

理论计算表明，活载作用下，混凝土边拱的弯矩效应大于轴力效应，主拱轴力效应大于弯矩效应，结合桥梁的受力控制断面，确定桥梁静力试验工况见表1，典型工况应力测试结果见表2，挠度测试结果见表3。

表1 静力试验工况

表2 主拱L/2最大轴力加载应力测试结果

表3 主拱L/2最大位移加载挠度测试结果

由以上结果可以看出，各加载工况下，结构控制断面的应力和挠度校验系数均不大于1，说明结构强度满足要求，有一定的安全储备。静力刚度良好，结构有着良好的弹性工作性能。应力、挠度实测结果与理论值基本吻合，分布规律也基本一致，说明在有限元计算分析中采用统一理论法计算结构刚度，考虑结构为压弯结构的理论假设是基本正确的。

5 动力试验结果

桥梁结构动力特性测试结果见表4，结构1阶、2阶、3阶振型见图6、图7、图8。

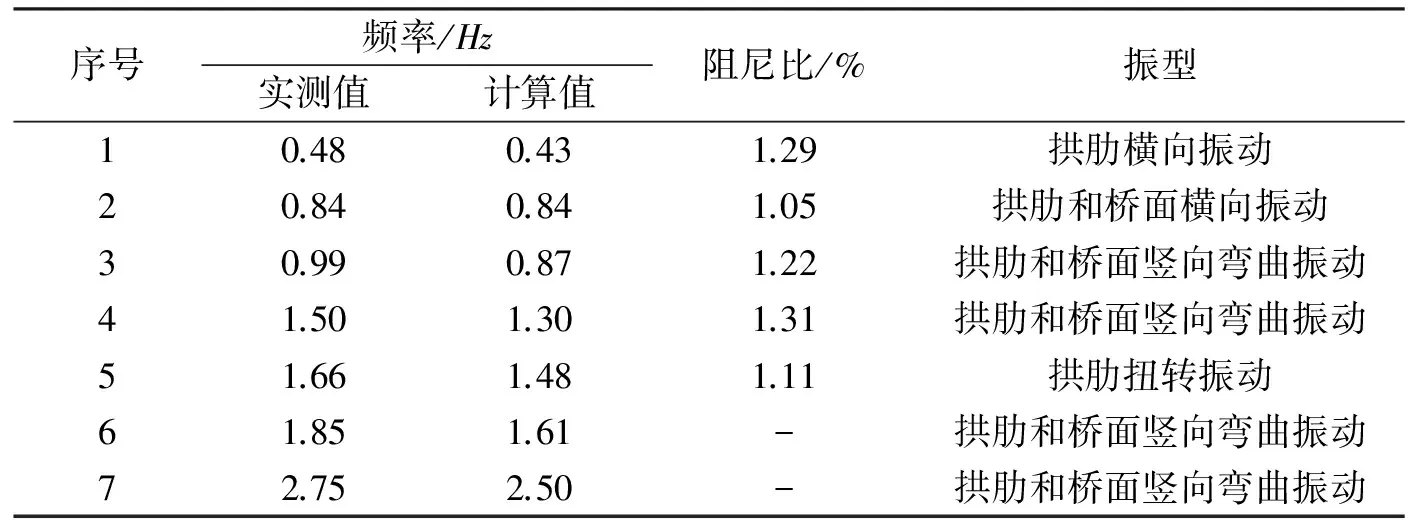
表4 动力特性测试结果

图 6 结构1阶振型

图 7 结构2阶振型

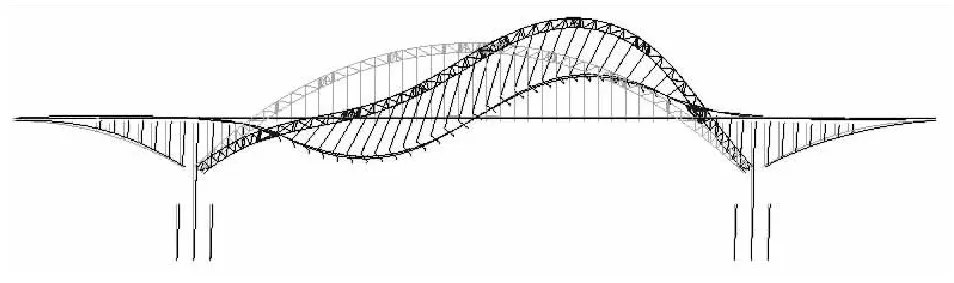
图 8 结构3阶振型

1)结构第1阶和第2阶振型均为面外横向振动，第3阶振型为面内竖向弯曲振动，说明拱肋面外刚度比面内刚度略小[4-5]，实测结果符合钢管混凝土拱桥动力特性的普遍规律，在桥梁设计时，应布置足够的横撑，且合理设置在桥跨范围内，来增加拱肋横向刚度，提高拱的整体稳定性。

2)由第1阶、第2阶和第5阶振型可以看出，桥面系的面内振动和拱肋基本同步，对于主拱，由于采用了柔性吊杆，桥面系的面外振动与拱肋相对独立，对于边拱，由于采用了立柱结构，桥面系的面外振动与拱肋基本同步。

3)实测自振频率、振型与理论值有着较好的吻

合性，说明采用子空间迭代法计算动力特性基本正确。

6 结语

1)钢管混凝土拱桥使用阶段计算分析中，采用将钢管混凝土整体看作一种复合材料的统一理论法计算截面刚度能基本反映结构的真实受力情况，有较强的实用性。

2)钢管混凝土拱桥实测面内基频比面外基频略小，说明拱肋面外刚度小于面内刚度，在设计时应重视横向刚度问题，通过合理设置横撑等措施，保证拱的整体稳定性。

[1] 黄继笑. 大跨中承式钢管混凝土静动力特性分析及试验研究 [D].西安：长安大学，2011.

[2] 严圣友,郑江敏，项贻强等.哑铃型钢管混凝土拱桥的计算方法研究 [J].公路交通科技，2004(6):54-57.

[3] 陈宝春.钢管混凝土拱桥[M].北京:人民交通出版社，2007.

[4] 董晓兵,陈毓娟.五跨钢管混凝土系杆拱桥的地震响应分析 [J].公路2016(2):98-102.

[5] 曾森,高龙涛,陈少峰.钢管混凝土拱桥多振型组合pushover方法可行性例证[J]土木工程学报,2016,49(1):80-85.

[责任编校： 张岩芳]

Stress Analysis of Concrete Filled Steel Tube Arch Bridge Using Stage

ZHOU Jinzhi1，XIE Ying1，JIANG Gan2

(1SchoolofCivilEngin.,ArchitectureandEnvironment,HubeiUniv.ofTech.，Wuhan430068,China; 2BridgeScienceResearchInstituteLtd.,ChinaRailwayMajorBridgeEngin.Group,Wuhan430034,China)

The paper first discusses the value of the stiffness of the calculation theory of concrete filled steel tubular arch bridges, and analyses the static and dynamic characteristics of the arch bridge under the serviceability limit state, Taking Yunxian Hanjiang Bridge as an example, the paper then calculates and analyzes the mechanical characteristic of the arch bridge when it is in use ,using finite element method, and finally verifies it the use of a load test method.

concrete filled steel tube arch bridge; rigidity; Static characteristics; dynamic characteristics

2016-02-28

周金枝(1964-)，女，湖北武汉人，湖北工业大学教授，研究方向为工程结构计算及仿真，桥梁结构病害分析及检测

谢 瑛(1990-)，女，湖北武汉人，湖北工业大学硕士研究生，研究方向为工程力学

1003-4684(2017)02-0088-04

U466.1

A