基于改进小波变换的语音基音周期检测

吴兴铨，周金治

(1.西南科技大学信息工程学院，四川 绵阳 621010;2.西南科技大学特殊环境机器人技术四川省重点实验室，四川 绵阳 621010)

基于改进小波变换的语音基音周期检测

吴兴铨1,2，周金治1,2

(1.西南科技大学信息工程学院，四川 绵阳 621010;2.西南科技大学特殊环境机器人技术四川省重点实验室，四川 绵阳 621010)

基音在许多方面都有比较广泛的应用，比如语音编码、语音识别、语音转换、音乐检索以及发声系统疾病诊断等。针对目前很多小波变换方法在测量基音周期时存在的准确度低、复杂度高、鲁棒性差等缺点，以及在带噪语音环境下，特别是在非平稳噪声下比较难判断语音基音周期的问题，提出了一种基于改进小波变换的语音基音检测方法。首先将每帧带噪信号进行预处理，提取出有话段的信息，消除直流分量；然后在加窗分帧后先进行端点检测，滤波后再分帧；接着再利用小波分解后取低频系数重构信号；最后结合四阶累积法对重构信号进行基音检测。试验结果表明，该方法在不同带噪语音环境下和低信噪比条件下，提高了带噪语音基音检测的准确性。与传统的小波变换法相比，该方法鲁棒性好且计算复杂度低，有利于语音基音周期检测。

带噪语音； 基音检测； 小波变换； 重构信号； 三电平中心削波； 端点检测； 信噪比

0 引言

基音是语音信号的重要参数，语音信号中的音高由基音频率[1]得到。基音广泛应用于各个领域，如语音编码、语音识别、语音转换、音乐检索以及发声系统疾病诊断等[2]。近年来，基音检测方法层出不穷，其中具有代表性的方法有自相关函数法、平均幅度差函数法、阴阳估计法、基于滤波器的算法、倒谱分析法、多分辨率法和离散小波变换法[3]等。因为语音信号是一个非平稳、非准周期的信号，会受到声道共振峰的影响，所以到目前为止，基音检测的准确性仍较受关注。上述所列的方法虽然在处理基音检测上有一定的可行性，但在稳定白噪声的环境下信噪比(signal noise ratio，SNR)会下降到0 dB，基音检测的准确率不高，仅采用小波变换的基音检测准确率能达到80%[4]。

宋子荣等提出的小波算法[5-6]能很好地适应语音信号的时变特性，计算复杂度也适中。但小波算法也有不足：它比较容易受到噪声和共振峰的影响，在基音检测的计算上产生偏差。文献[7]采用改进的小波转换，该方法削弱了噪声、降低了计算复杂度，但是计算准确率不高。本文提出了一种改进的语音基音周期检测的方法，在低信噪比环境下不仅能大大提高基音检测的准确性，还能提高其鲁棒性。

1 小波变换原理

小波变换主要包含两个部分：连续小波变换(continuous wavelet transform，CWT)和离散小波变换(discrete wavelet transform,DWT)。CWT主要用于理论分析，通过伸缩和平移参数连续取值，而计算机和工程化角度的处理实现往往采用DWT[8]。

1.1 连续型小波变换

在连续小波变换[9]中，平方可积分函数s(t)的连续小波变换定义为：

(1)

式中：s(t)为原始信号；<*,*>为内积；a>0为尺度因子；b>0为平移因子；Ws()为信号s(t)的傅里叶变换；Ψa,b(t)为小波变换基函数Ψ(t)的尺度伸缩a和时间平移b所产生的一族解析函数的结果，常数a和b分别为尺度参数和平移参数。Ψa,b(t)中尺度参数a的伸缩和平移参数b的平移为连续取值的小波变换称为连续小波变换。

1.2 离散型小波变换

(2)

式中：当a=2、b=1时，离散小波变换称为二进制离散小波变换[10]。

2 改进的小波变换基音检测

在非平稳、非线性的语音信号中，噪声的能量明显低于语音段的能量[11]。在实际应用中，经常会有一些强噪声的干扰，比如火车、汽车鸣笛、移动通信环境、机械环境等。低SNR下的基音检测是语音研究中的难点，传统的方法都存在一些不足：基于子带能量、周期度量的方法只适用于某些噪声环境；基于熵的方法对多路的串扰噪声效果不好；基于特征滤波的方法不仅会增大计算量，而且会改变语音语谱结构、丢失原数据的部分信息[12]。所以从计算量，以及在不同特征情况下得分组合权重参数的鲁棒性考虑，以上方法都无法从根本上解决噪声环境下的基音检测问题。

信号处理中常假设信号或噪声服从高斯分布，即在常规的信号处理中，用二阶积累量表示随机信号的统计特性与关系。任何类型高斯信号的三阶以上高阶累积量均为0。高阶累积量的这种特性可用于抑制噪声，所以使用高阶累积量作为分析工具，对抑制噪声有较好效果[13]。本文在采用小波分解后取低频系数重构信号，结合四阶累积法对重构信号进行基音检测。

累积量是语音信号中一种比较重要的统计特征。现有均值为0的复平稳随机语音信号{X(n)}，n=0,±1,…，±∞，其二阶累积量为：

C2,x(τ)=E{x(n)x*(x+τ)}

(3)

三阶累积量为：

C3,x(τ1,τ2)=E{x(n)x(n+τ1)x*(n+τ2)}

(4)

四阶积累量为：

C4,x(τ1,τ2,τ3)=E{x(n)x(n+τ1)x*(n+τ2)x*(n+τ3)}-E{x(n)x(n+τ1)}E{x*(n+τ2)x*(n+τ3)}-E{x(n)x*(n+τ2)}E{x(n+τ1)x*(n+τ3)}-E{x(n)x*(n+τ3)}E{x(n+τ1)}x*(n+τ2)}

(5)

由上式可得：任何类型的高斯语音信号，其三阶以上的高阶累积量均为0。

假设语音信号为s(t)，高斯噪声为n(t)，则带噪语音信号表示为:

x(t)=ps(t)+qn(t)

(6)

式中：p和q为增益系数。检测二元语音基音时，若采用传统的基音检查方法，则能明显观察到，当SNR下降时，检测的准确性急剧下降。为了实现即使在SNR很小时，也可以得到较好的检测结果，需要计算语音信号四阶积累量。在前文所述的高阶累积量中可以得出x(t)的四阶累积量。因为任何类型的高斯信号其三阶以上的高阶积累量均为0，所以可以将计算语音信号四阶积累量的问题转换成计算带噪语音信号四阶积累量的问题。本文采用小波分解后取低频系数重构信号结合四阶累积法，对重构信号进行基音检测，一方面提高了基音检测的准确性，另一方面也控制了计算量，且不改变语音谱结构，保存了完整的语音信息。

在计算带噪语音信号的时候，运算量非常大，其根本原因就是计算机进行的乘法运算非常耗时。因此，可以采用三电平中心消波的方法对中心消波函数进行修正。使用三电平中心消波后，可以有效避免错判为倍频或分频的情况。将语音信号通过三电平中心削波器削波。三电平中心削波函数如图1所示。

图1 三电平中心削波函数

由图1可知，其输出函数为：

(7)

根据式(6)可知，输出为x(t)。式(5)则说明了四阶积累量的值，基于四阶积累量的基音检测推导出所用的自相关函数为：

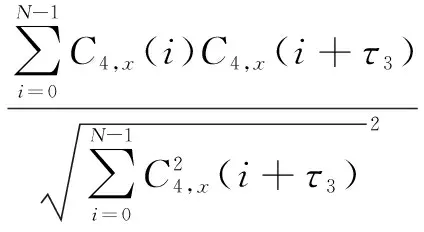
(8)

式中：N为窗长度。求得R的峰值位置后，将这些峰值的门限进行比较，相邻峰值的时间差就是基音周期。

经试验，在低SNR环境下，自相关法根本无法进行基音检测，得到的结果也是错误的，而用高阶累积量则可以准确、可靠地检测基音周期。本文就是利用小波分解后取低频系数重构信号[14]，结合四阶累积法对重构信号进行基音检测。该方法的准确性优于带噪信号下传统基音检测的方法，解决了在低SNR环境下无法得到准确信号的问题。试验表明，该方法无论在低信噪比，还是在噪声分布不均匀的条件下，对基音周期都具有良好的检测效果，且不会出现试验数据准确率骤然下降的现象，显示了非常好的鲁棒性。

假设带噪语音信号为x(t)，基音检测的步骤如下。

①对每帧带噪信号进行预处理，提取出有话段的信息，得出语音段[15]。

②消除直流分量，设置信噪比，叠加噪声；用所提取的有话段的信息作DWT小波变换，用低频系数重构信号。引入Cum表示累积量运算，则若有λi(i=1,2,…,k)、xi(i=1,2,…,k)为随机变量，推导出：

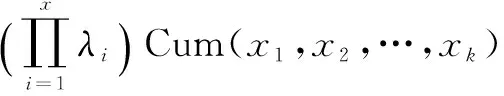
(9)

由前一节可知，s(t)与n(t)独立，由式(9)可以得到x(t)的四阶累积量：

Cum[x(k+ξ1)x(k+ξ2)x(k+ξ3)x(k+ξ4)]=a4×Cum[x(k+ξ1)x(k+ξ2)x(k+ξ3)x(k+ξ4)]+b4×Cum[k+ξ1)x(k+9ξ2)x(k+ξ3)x(k+ξ4)]

(10)

③对判断出的语音段进行基音检测。根据得到的基音周期图判断算法的准确性和鲁棒性。

3 试验结果与分析

3.1 试验环境

为了检测本文方法的可行性和有效性，选择深夜或相对比较安静环境，在试验室录制内容为“西科大”的一小段语音作为目标语音信号。设定录制的采样频率为8 kHz，采样精度为 32 bit；目标语音信号帧长为 316 ms，帧移为158 ms；采用标准噪声库NOISEX-92中的高斯白噪声、babble以及 factory作为复杂干扰噪声[4]。

3.2 结果分析

对原始语音波形图加入信噪比SNR=-10 dB的高斯白噪声后，对该加入噪声的语音信号进行预处理，提取有话段的信息，得出语音段，消除直流分量，在加窗分帧后先进行端点检测，滤波后再分帧，小波分解后取低频系数重构信号。原始信号、加噪语音信号和重构语音信号波形图如图2所示。

图2 原始信号、加噪语音信号和重构语音信号波形图

令SNR=-5 dB，用四阶累积法对重构信号进行基音检测，其结果如图3所示。

图3 基音检测结果(SNR=-5 dB)

为了更好地验证算法的准确性，也为了进一步验证本文方法在低信噪比环境下的检测效果，图4为采用本文方法、在SNR=-20 dB时的基音检测结果。

图4 基音检测结果(SNR=-20 dB)

由图4可以看出，采用本文方法对小波变换进行改进，大大提高了低信噪比下基音检测的准确性和鲁棒性。

本文通过大量的样本训练得出训练结果，并与文献[2]中数据结果相比，列出了各种噪声下的准确率结果。表1记录了采用小波-自相关函数加权平均幅度差函数的方法和本文方法在不同噪声环境下的准确率。

表1 不同信噪比下的基音检测准确率

由表1可知，与文献[2]方法相比，本文方法的基音检测准确率提高了20%以上。本文方法在低信噪比环境下，大大提高了基音检测准确性及其鲁棒性。

4 结束语

基音检测对语音信号的后期处理具有至关重要的作用，准确检测语音信号的基音周期对高质量的语音分析与合成、语音压缩编码、语音识别与说话人确认等具有重要意义[16]。本文提出了一种小波分解后取低频系数重构信号，结合四阶累积法对重构信号进行基音检测的方法。试验表明，该方法的基音检测准确率明显高于目前已有的一些方法，并且在加入高斯白噪声、低信噪比的情况下，也能得到比较精确的基音周期，提高了整个系统的鲁棒性。

[1] 唐振民,曹建红．基于哼唱的音乐检索技术研究[D]．南京:南京理工大学,2009.

[2] 王民,曹绘,要趁红.一种改进的小波变换基音检测算法[J].重庆邮电大学学报(自然科学版),2012,24(3):283-287.

[3] 张杰,龙子夜,张博,等.语音信号处理中基频提取算法综述[J].电子科技大学学报,2010(S1):99-102.

[4] 章小兵,李燕萍,王双杰.基于改进HHT的语音端点检测[J].计算机工程,2016(6):171-174.

[5] HU J L,XU S,CHEN J．A modified pitch detection algorithm[J]．IEEE Communications Letters，2001,5(2):64-66.

[6] 宋子容,袁春,温启荣.小波分析法对多带激励声码器基音提取的改进[J].重庆邮电学院学报,1997(2):33-37.

[7] 李坤,刘加.基于小波变换和线性预测的基音提取[J].计算机工程,2010(10):276-278.

[8] 胡航.现代语音信号处理[M].北京:电子工业出版社,2014.

[9] 张贤达.现代信号处理[M].北京:清华大学出版社,2002.

[10]热依木汗·热西提,吐尔洪江·阿布都克力木,冯惠,等.基于二进小波变换的语音基音检测[J].科技展望,2016(11):111-112.

[11]GUO Y M,FU Q,YAN Y H.Speech endpoint detection in real noise environments[J].Chinese Journal of Acoustics,2007,26(1):39-48．

[12]孙海英.基于倒谱特征和浊音特性的语音端点检测方法的研究[D].青岛：青岛科技大学,2008.

[13]金晶.短波通信系统中8PSK调制方式识别技术的研究[D].西安：西安电子科技大学,2012.

[14]史振江,安建龙,赵玉菊.基于MATLAB的小波消噪仿真实现[J].石家庄铁路职业技术学院学报,2008(1):63-66.

[15]陈炜杰.噪声环境下的说话人识别技术研究[D].杭州：浙江工业大学,2008.

[16]张少龙,吴佳鑫.语音信息的内容分析技术研究综述[J].现代图书情报技术,2007(4):28-31.

Speech Pitch Period Detection Based on Improved Wavelet Transform

WU Xingquan1,2，ZHOU Jinzhi1,2

(1.School of Information Engineering,Southwest University of Science and Technology,Mianyang 621010,China;2.Robot Technology for Special Environment Key Laboratory of Sichuan Province,Southwest University of Science and Technology,Mianyang 621010,China)

Pitch has been widely used in many areas,such as speech encoding,speech recognition,speech conversion,music retrieval and diagnosis of diseases of vocal system.Aiming at the disadvantages of pitch period measurement based on wavelet transform,e.g.,low accuracy,high complexity and poor robustness,and the problem of the difficulty of judging the speech pitch period under noisy speech environment,especially under non-stationary noising,the speech pitch period detection method based on the improved wavelet transform is proposed. Firstly,each frame of noisy signal is preprocessed to extract the information with speech segments and eliminate the DC component.Then,endpoint detection is conducted after window-added framing,and re-framing after filtering; and then the low frequency coefficient reconstructed signal is extracted after using wavelet decomposition.Finally,the pitch detection for the reconstructed signal is accomplished combining with the fourth order cumulative method.The experimental results show that under different noisy speech environment and low SNR condition,the accuracy of noisy speech pitch detection is improved.Comparing with the method of traditional wavelet transform,this method features better robustness and low computation complexity,these are helpful in speech pitch period detection.

Noisy speech; Pitch detection; Wavelet transform; Restructured signal; Three-level center clipping; Endpoint detection；SNR

特殊环境机器人技术四川省重点实验室基金资助项目(13ZXTK07)

吴兴铨(1992—)，男，在读硕士研究生，主要从事语音识别、软件开发等技术的研究。E-mail:304094795@qq.com。 周金治(通信作者)，男，硕士，副教授，主要从事计算机网络与物联网、智能家居、语音识别等技术的研究。 E-mail:zhoujinzhi@swust.edu.cn。

TH-3;TP391.4

A

10.16086/j.cnki.issn1000-0380.201706016

修改稿收到日期：2017-03-16