土豆片微波真空干燥动力学模型的研究

杨绮云，丁 睿

(哈尔滨商业大学 轻工学院，哈尔滨150028)



土豆片微波真空干燥动力学模型的研究

杨绮云，丁 睿

(哈尔滨商业大学 轻工学院，哈尔滨150028)

以土豆片为原料，研究了土豆片微波真空干燥过程中，水分比随时间变化的动力学模型.以微波功率、切片厚度及装载量为三因素进行实验，通过对实验数据的分析，得出符合土豆片微波真空干燥动力学特性的模型为Page模型.用SPSS软件对模型进行拟合，得出最终的干燥动力学方程，并通过实验进行验证，证明用Page模型描述土豆片微波真空干燥过程的动力学特性效果良好.

微波真空干燥；动力学模型；土豆片

土豆一直以来都受到人们的欢迎，是人们日常餐饮的一部分.土豆具有抗衰老的功效，含有丰富的维生素.土豆干可长期存储，在北方冬季缺少蔬菜的时候，是一道难得的美味佳肴，传统的土豆干制作方式主要采用的是晾晒干燥方式.

微波真空干燥技术是一项受到国内外干燥行业广泛研究和关注的新型干燥技术，可达到提高产品品质、降低成本、减少干燥时间等目的[1].采用微波真空干燥技术干燥的土豆片外表呈金黄色，干燥时间短，干制品复水性较好，是相对更节能高效的干燥方式.

限于现代干燥技术，要实现物料在干燥过程中水分的实时在线监测仍是个难题，因此对干燥过程中水分的变化规律进行研究，将会为实际生产提供更多理论依据[2].而在食品干燥的研究中，动力学模型正是可以描述物料水分比随干燥时间变化的函数[3].目前国内外对土豆片微波真空干燥的动力学模型部分的研究甚少[4].因此，本文将对土豆片微波真空干燥过程中的动力学模型进行研究，使今后在土豆片微波真空干燥的实际生产及实验过程中可以较准确的把握其水分和时间的变化规律.

1 干燥动力学模型模型的选择

物料干燥的过程中涉及到很多复杂的传热传质过程，因此建立物料干燥动力学模型对研究干燥规律及工艺参数具有重大意义.同时，模型选择的合适与否也将直接影响实验值与预测值的误差大小.目前常用的薄层物料干燥模型主要有以下几种[5-8]：

1)指数模型Lewis：MR=e(-kt)

该模型是最早用于薄层物料干燥的数学模型之一，主要考虑了物料表层及边界层对水分扩散运动的阻力[9].

2)单项扩散模型Henderson：MR=Ae(-kt)

该模型是由Henderson等人根据菲克定律推导出并简化得到的半理论方程，已被用于描述带穗谷物、小麦和玉米等物料的干燥动力学特性.

3)Page方程：MR=exp (-ktn)

该模型是对Lewis修正后得到的，用于描述玉米、向日葵、稻谷、大豆、人参、罗非鱼鱼片等多种物料的薄层干燥特性[10].

4)Logarithmic模型：MR=Ae(-kt)+c

5)Wang：MR=1+at+bt2

该模型由 Wang 等人在Thompson方程的基础上转化而来.MR为水分比，

MR=(Mt-Me)/(M0-Me)；

其中:t为干燥时间(min)；Mt为t时刻物料含水率(干基)；Me为平衡含水率(干基)；M0为初始含水率(干基)；

由于微波真空干燥物料的平衡含水率Me资料很少，且实验很难获得，故把水分比MR简化为：MR=Mt/M0[11].

本项研究采用JDH—4GZ型微波真空干燥设备，对土豆片进行微波真空干燥实验.

实验方案：选用同批次，大小相近的土豆进行微波真空干燥实验，在真空度为-0.085 MPa的条件下，取微波功率(1、2、3 kW)、切片厚度(4、8、12 mm)、装载量(800、1 070、1 340 g)为三个因素，每组实验均干燥至土豆片含水率≤20%为止，做出每组实验下的时间t与水分比MR曲线图，如图1～3所示.由图可以看出这些曲线均大致呈指数形式，因此在上述常用干燥模型中，初步确定土豆片微波真空干燥的动力学模型在Lewis、Henderson、Page以及Logarithmic这四种指数形式的模型范围中.

图1 不同微波功率下的土豆片t-MR曲线图

图2 不同切片厚度下的土豆片t-MR曲线图

图3 不同装载量下的土豆片t-MR曲线图

分别对Lewis、Henderson、Page以及Logarithmic模型进行线性化处理，即将各模型等式两边分别取对数，可以相对应的得到式(1)～(4).

ln(MR)=-kt

(1)

ln(MR)=lnA-kt

(2)

ln[-ln(MR)]=lnk+nlnt

(3)

ln(MR)=ln(Ae(-kt)+c)

(4)

同样根据上述实验中的实验数据，分别作不同微波功率、切片厚度以及装载量下的—-ln(MR)曲线(图4～6)和lnt-ln[-ln(MR)]曲线(图7～9).由下图不难看出，-ln(MR)与t呈非线性，ln[-ln(MR)]与lnt呈线性.

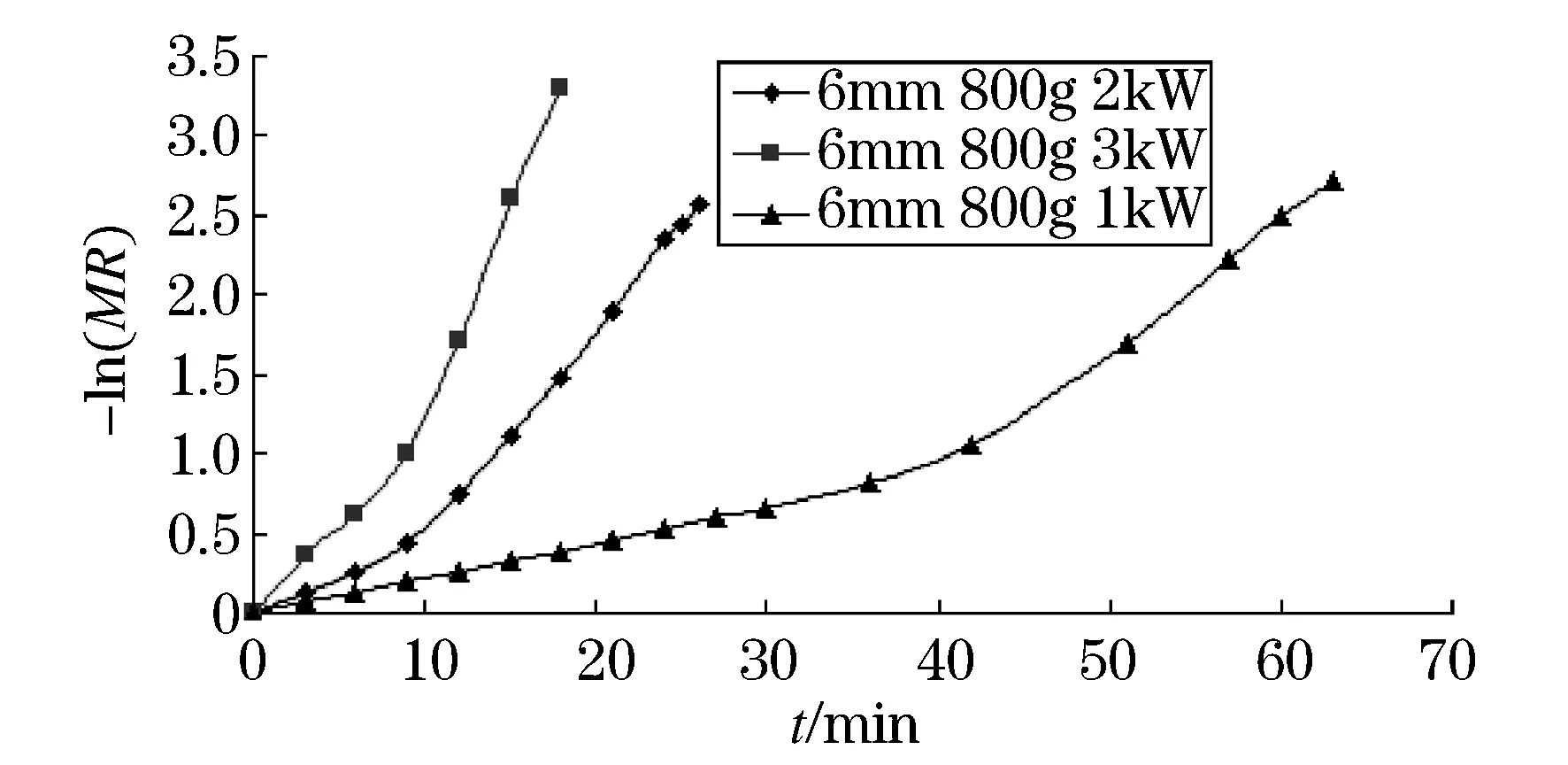
图4 不同微波功率下的土豆片t-ln(MR)曲线图

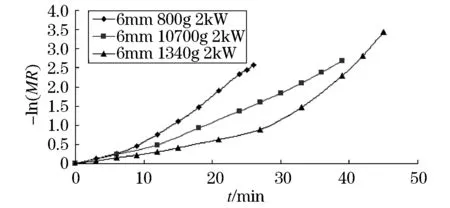
图5 不同装载量下的土豆片t-ln(MR)曲线图

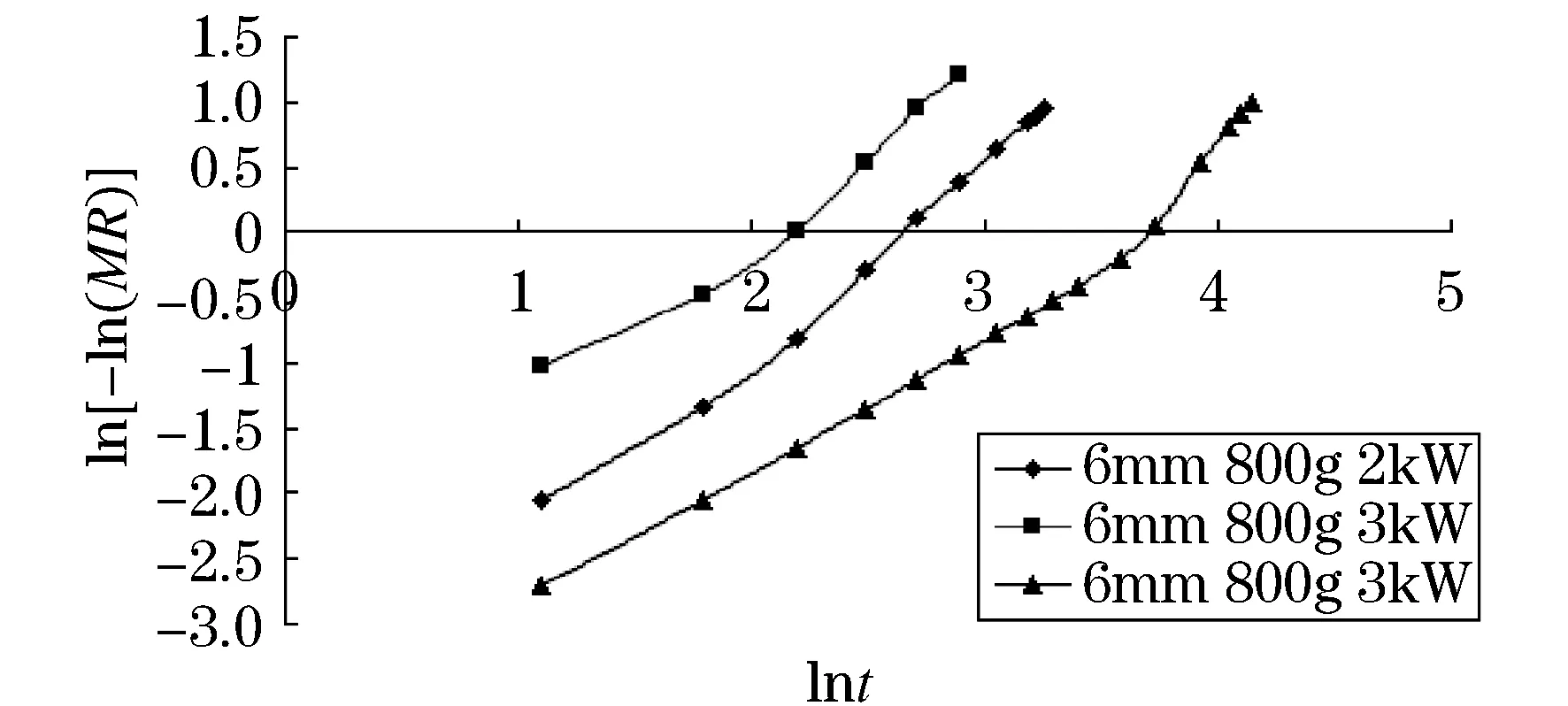
图7 不同微波功率下的土豆片lnt-ln[-ln(MR)]曲线图

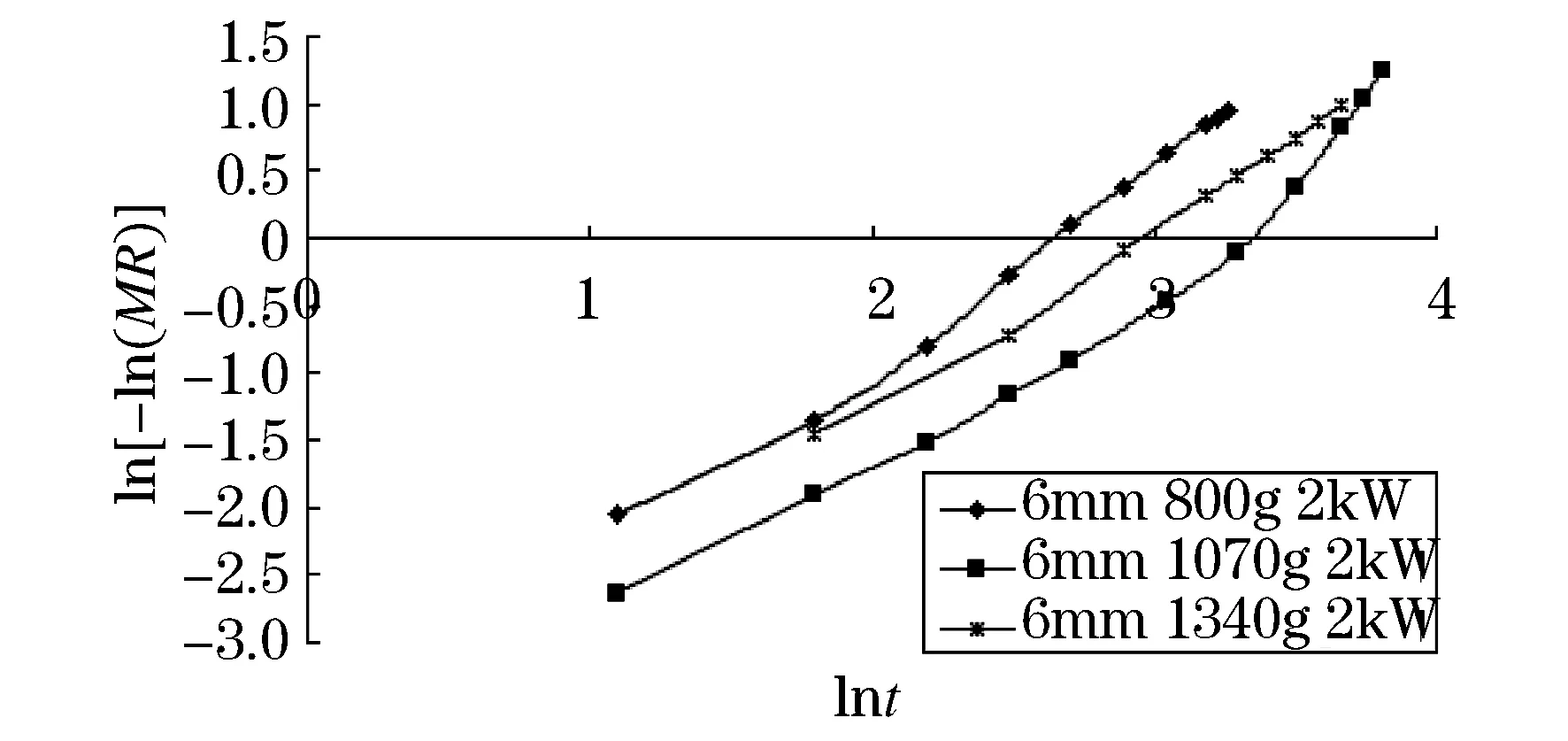
图8 不同装载量下的土豆片lnt-ln[-ln(MR)]曲线图

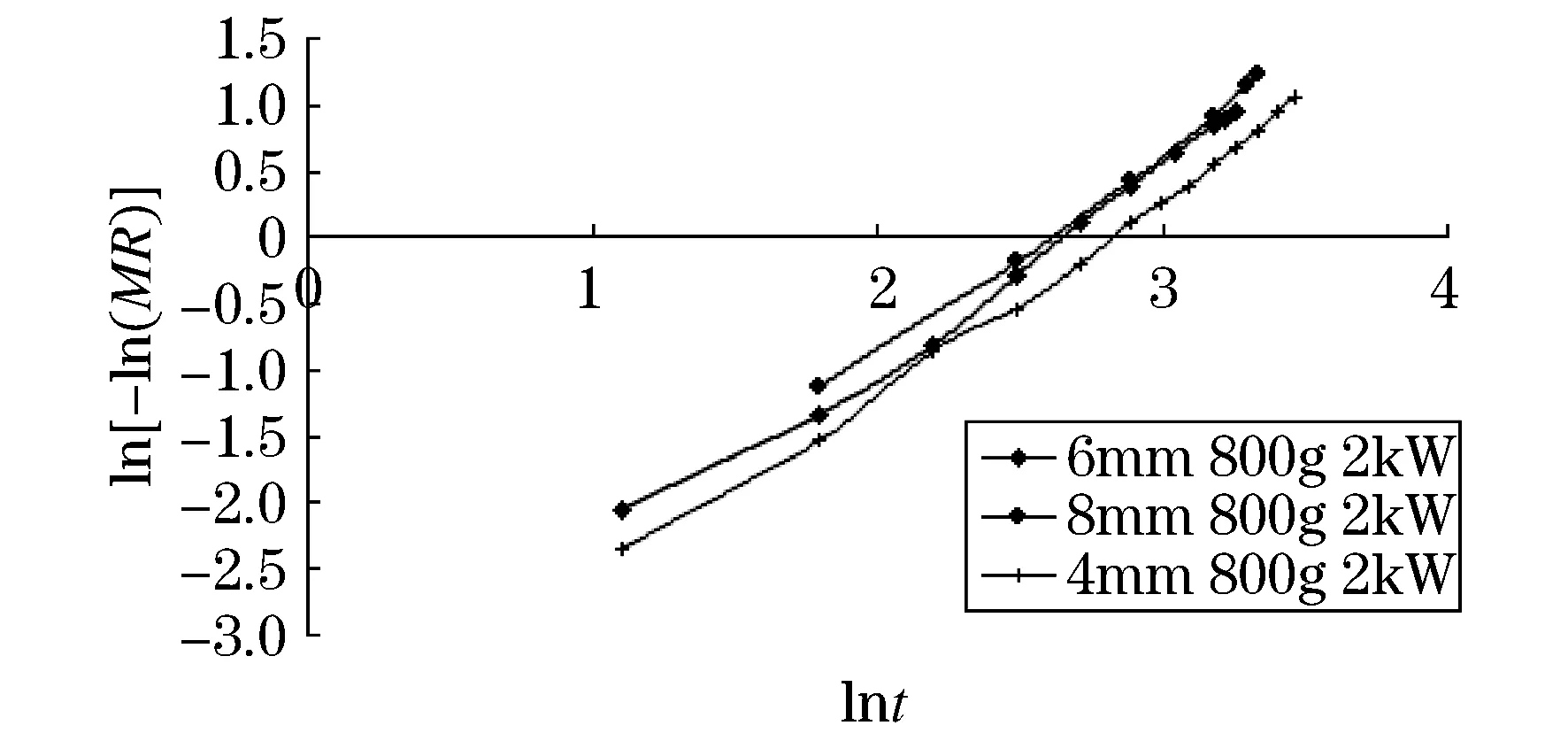
图9 不同切片厚度下的lnt-ln[-ln(MR)]曲线图

在Lewis、Henderson、Page、Logarithmic这四种干燥模型中，图4～6可以看出，Lewis和Henderson模型的-ln(MR)与t呈线性，因此这两种模型不适合做土豆片的微波真空干燥动力学模型.图7～9可以看出，Page模型的ln[-ln(MR)]与lnt呈线性，符合模型要求.Logarithmic模型既不符合-ln(MR)与t呈非线性的规律，也不符合ln[-ln(MR)]与lnt呈线性的规律，也可以排除.由此可以得出，土豆片的微波真空干燥动力学模型满足Page方程：MR=exp(-ktn).

2 动力学模型的拟合

用SPSS软件对土豆片微波真空干燥动力学方程进行拟合，从而得出模型中的各个系数.在Page模型MR=exp(-ktn)，即ln[-ln(MR)]=lnk+nlnt中，令：

lnk=a+bX1+cX2+dX3

(5)

n=e+fX1+gX2+hX3

(6)

其中:X1为微波功率，kW；X2为切片厚度，mm；X3为装载量，g；a、b、c、d、e、f、g、h为待定系数.

将式(5)、(6)带入Page方程：MR=exp(-ktn)，即ln[-ln(MR)]=lnk+nlnt中可得到：

ln[-ln(MR)]=(a+bX1+cX2+dX3)+(e+fX1+gX2+hX3)lnt.

(7)

利用SPSS软件，将上述实验中得到的实验数据带入方程(7)中，并进行线性拟合，求得方程各待定系数，去除不显著项.得到的回归方程如下：

ln[-ln(MR)]=(-4.417+0.593X1+0.11X2-0.001X3)+(1.07+0.168X1-0.009X2+4.295×10-5X3)lnt

回归方程的R2=0.977，F=379.578，P<0.001说明模型拟合度良好，实验误差较小.在实际生产及实验中，根据该方程可以计算得出不同微波功率、切片厚度及装载量下，水分比随时间的变化规律，从而可以更好的把握干燥终点时间，使土豆片在干燥过程中不易过热.

3 动力学模型的验证

在真空度为-0.085 MPa时，选取微波功率2 kW、切片厚度6 mm、装载量1 231 g进行模型验证实验.图10为该实验条件下分别根据预测值和实际测量值绘制的干燥曲线，表明两条干燥曲线无显著差异.因此认为该模型可描述土豆片微波真空干燥过程中水分的变化情况.

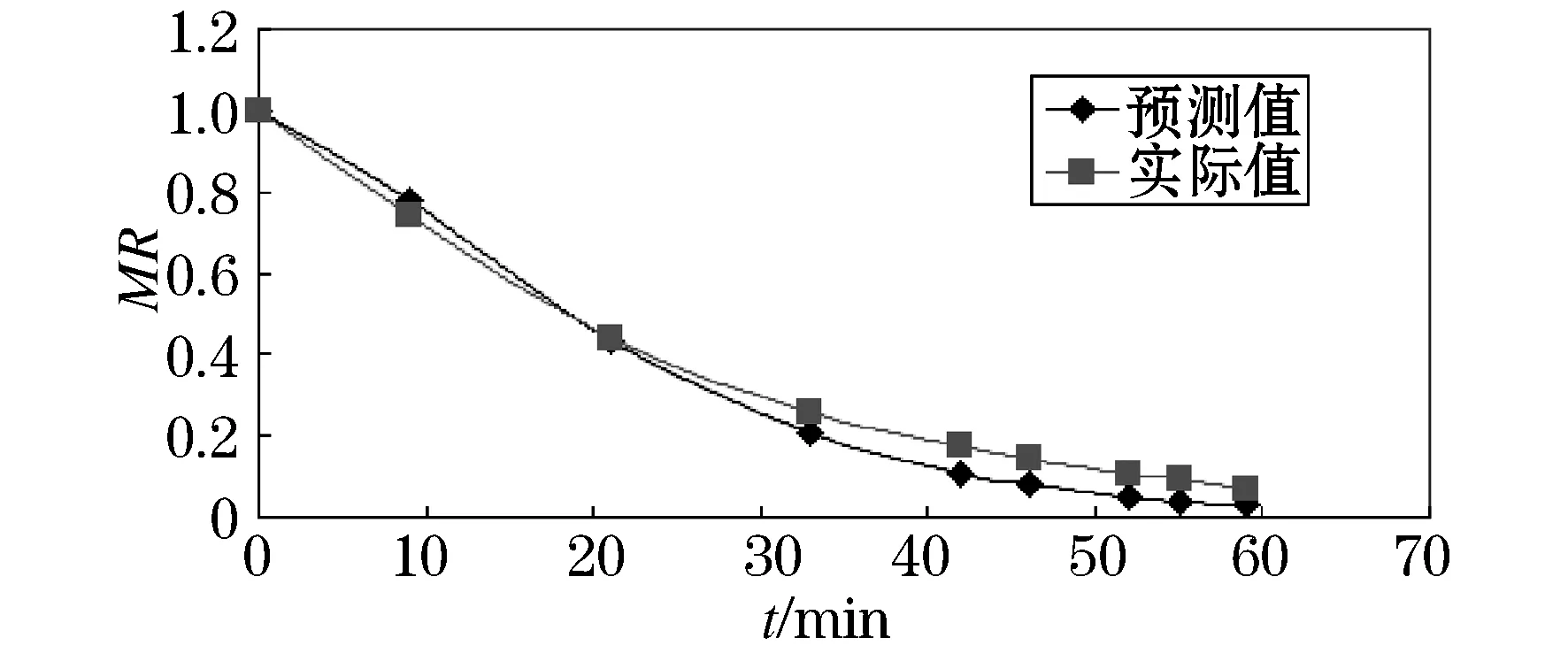
图10 相同条件下实验值与预测值的比较

4 结 语

通过对实验数据的分析，确定了符合土豆片微波真空干燥的动力学模型为Page模型；利用SPSS软件对模型进行线性拟合，得出了土豆片微波真空干燥过程的动力学模型方程，该方程R2=0.977，模型拟合F=379.578以及P<0.001，均说明确定的动力学模型方程拟合呈显著，拟合效果良好；对动力学模型进行验证， Page方程预测值与实验值拟合良好.利用此动力学模型方程可以较准确地预测土豆片微波真空干燥过程中含水率随时间的变化规律，解决土豆片在干燥过程中水分含量实时在线监测困难的问题，为今后土豆片的实际生产和实验提供了理论参考.

[1] 武凯卓. 金丝小枣干燥方法的研究[D]. 天津: 河北工业大学, 2013.

[2] 胡庆国,卜召辉, 陆 宁. 金针菇真空微波干燥动力学模型的研究[J]. 食品与机械, 2010, 05: 48-42.

[3] 王安建, 高帅平, 田广瑞, 等. 花生热泵干燥特性及动力学模型[J]. 农产品加工, 2015, 05: 57-60.

[4] 林向阳, 张丽晶, RUAN R, 等. 茶叶真空微波干燥特性及动力学模型[J]. 中国农学通报, 2010, 26(22): 65-70.

[5] 段振华, 张 慜, 汤 坚. 鳙鱼的热风干燥规律研究[J]. 水产科学, 2004, 23 (3): 29-32.

[6] 崔政伟. 微波真空干燥的数学模拟及其在食品加工中的应用[D]. 无锡: 江南大学, 2004.

[7] 王宝和. 干燥动力学研究综述[J]. 干燥技术与设备, 2009, 7(1): 51-56.

[8] BABALIS S J, PAPANICOLAOU E, KYRIAKIS N,etal. Evaluation of thin-layer drying models for describing drying kinetics of figs (Ficus carica) [J]. Journal of Food Engineering, 2006, 75: 205-214.

[9] 王红提, 郭康权, 李 鹏, 等. 疏解棉秆的微波干燥动力学及能耗分析[J]. 农业工程学报, 2015, 19: 294-301.

[10] 徐成发, 段振华, 杨 毅. 罗非鱼片的渗透微波复合干燥特性[J]. 中国科技纵横, 2011, 17: 343-345.

[11] 茹塞红. 微波流化床干燥技术和设备的开发应用[D]. 广州: 广东工业大学, 2012.

Study on mathematical model of water loss in microwave-vacuum drying

YANG Qi-yun，DING Rui

(School of Light Industry, Harbin University of Commerce, Harbin 150028, China)

The potatoes were used as materials to study on the mathematical model of water loss in microwave-vacuum drying. The effects of different factors including microwave power, slice thickness and loading were investigated. Find out the microwave-vacuum drying of potato chips was in good agreement with the Page model. By SPSS software, the mathematical drying modeling and verification were processed and it proved that the Page model was matched.

microwave-vacuum drying; mathematical model; potato chips

2016-10-21.

杨绮云(1959-)，女，教授，研究方向：食品机械研究与开发.

TS215

A

1672-0946(2017)03-0324-04