武装直升机编队对地攻击兵力需求计算模型研究
苗李达,王宗杰,孙守福
(海军航空工程学院,山东 烟台 264001)
武装直升机编队对地攻击兵力需求计算模型研究
苗李达,王宗杰,孙守福
(海军航空工程学院,山东 烟台 264001)
为解决兵力需求预测时对抗兵种单一、目标分配不明的问题,针对机载武器系统的性能特点,以规范交战方式为基础,定量描述了担负不同作战任务的兵力变化对作战结果的影响,建立武装直升机编队兵力需求计算模型,并结合作战情况要求,解算出最优兵力编组和挂载方案。实例验证结果表明,模型高效可信,能够为编队对地攻击兵力需求预测提供科学的理论依据。
武装直升机;编队;兵力;需求;分配
武装直升机编队兵力需求计算,是制定作战计划时的一项核心内容,需要考虑兵力在满足各种约束条件下的最大效能,或满足任务要求前提下的最小战损。由于进攻编队与防御体系的作战是十分复杂的过程,涉及众多因素,因此编队兵力需求计算也是一个动态不确定问题。文献[1-4]利用Lanchest方程或改进形式研究了不同作战模型的兵力需求问题。文献[5]采用系统动力学方法,定性分析了兵力需求的影响因素及其相互关系,定量研究了兵力需求相关变量间因果关系及需求变化的动态规律。文献[6]建立了基于任务的兵力需求优化模型,并利用马尔科夫过程理论以及概率分析法确定模型中的参数。但上述文献存在以下不足:文献[1-3]没有充分区分双方的对抗特点;文献[4-5]只考虑了双方单一武器系统之间,而没有考虑多种武器系统之间的对抗情况;文献[6]提出了对抗条件下的兵力需求构想,但没有相应具体实例,无法验证其效果。本文通过分析武装直升机不同武器系统的特点,基于文献[5-6]的3层防御体系假设,在规范交战方式下建立武装直升机编队兵力需求模型。最后,通过实例分析验证模型的有效性。
1 直升机编队武器系统与交战方式
武装直升机机载武器系统主要包括:空空导弹、空地导弹、火箭弹以及机枪(炮)等。按照不同的作战任务,有多种武器挂载方式,并且1架武装直升机可以同时挂载多种武器。
假设红方能够出动的直升机兵力足够多,并且作战任务已知。经过情报收集和战前分析,对蓝方目标群的数量、属性等基本情况均已掌握。同时得知,蓝方组建了针对红方编队的防御体系分为3道防线:直升机编队防线、地空导弹防线、高炮防线。红方突击编队需要依次突破3道防线后,才能对蓝方地面目标群实施打击。为取得最大突击效果并有效减少己方损失,红方编队分为2部分:一部分为压制兵力,负责对蓝方各层防线的兵力进行压制,尽最大可能削弱蓝方防御兵力;另一部分为突击兵力,负责突击经己方压制兵力削弱后的蓝方防线,实施对蓝方地面目标群的打击。双方交战关系如图1所示。
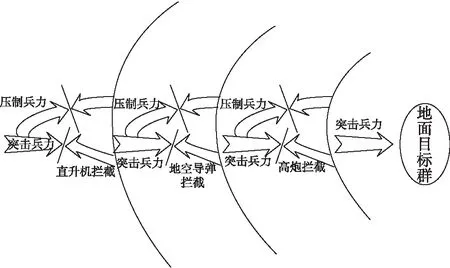
图1 直升机编队对地攻击示意图
双方按照规范方式交战[5]:担负不同任务的各兵力群,严格按照交战规则,顺次完成且只完成分配给自己的作战任务。按照这一要求,红方压制兵力先与蓝方防御兵力交战,突击兵力依次突破蓝方剩余防御兵力的3道防线后,再对地面目标群实施打击。为简化做如下规定:
1) 双方担负各自任务的兵力数量确定后,除因战损外,无其他变化;
2) 蓝方各道防线在与红方压制兵力交战结束后,剩余兵力仍有足够弹药对红方突击兵力实施拦截。
2 兵力需求计算模型构建
2.1 兵力部署建模
经过情报收集和战前分析,红方确定对蓝方共M类地面目标实施攻击,其中第j类目标的数量和单个目标价值分别为nj和ej(j=1,2,…,M),则蓝方地面目标群的总价值EM为
(1)
由于各类目标属性存在差异,并且不同种类弹药命中后产生的毁伤效果也不相同,因此,红方需要合理分配对蓝方目标实施攻击的飞机机型和挂载弹药。设红方可使用的对地攻击机型及弹药组合有N种(同种机型挂载不同弹药视为不同组合),Cij为毁伤能力系数,表示1架使用第i种机型及弹药组合的武装直升机(以下简称第i型机)能够毁伤第j类目标的个数。Yij为突击兵力元素,表示对第j类目标实施攻击的第i型机架数。
蓝方各道防线的兵力数量分别为f1、f2、f3,拦截能力系数Hki,表示第k道防线(k=1,2,3)单个兵力能够拦截红方第i型机的数量。
红方担负压制任务的机型和弹药组合有L种,压制能力系数Ilk,表示1架担负压制任务的第l型机能够毁伤或压制第k道防线的蓝方兵力数量。Xlk为压制兵力元素,表示对第k道防线实施压制的第l型机架数。
2.2 交战过程建模
按照规范交战方式,红方压制兵力先行对蓝方防御兵力实施压制,压制效果取决于Ilk和Xlk的取值,用gk表示蓝方各层防御兵力受到压制后的剩余兵力,则
(2)
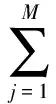
(3)
由于同机型并挂载同样武器的武装直升机的突防能力相同,所以在这里认为负责攻击不同目标的第i型机,能够成功突破3道防线的概率pi均为:
(4)
成功突破全部防线的第i型机可以对各自的任务目标实施打击,攻击第j类目标的第i型机一共可以毁伤该类目标mij个:
mij=Yij·pi·Cij
(5)
则突击编队总的毁伤价值即作战效能E为
(6)
将式(2)-(5)依次代入式(6),得
(7)
在兵力部署阶段,目标种类M、单个目标价值ej、各道防线的兵力fk、毁伤能力系数Cij、压制能力系数Ilk、拦截能力系数Hki以及红方机型和弹药组合数L、N均可知,则式(7)中的毁伤价值E只与突击兵力元素Yij以及压制兵力元素Xlk相关。
2.3 兵力需求约束建模
红方兵力需求受多个条件限制,根据作战目的和任务的不同,概括起来至少分为以下几个方面:
1) 对目标群总体造成不低于一定程度的毁伤:
E/EM≥A
(8)
2) 目标群中有某类(个)目标十分重要(如指挥所),必须将其严重毁伤,用Ej表示对此目标的实际毁伤:
(9)
3) 突击兵力的战损小于某特定值:
(10)
4) 出动兵力尽量少:
(11)
5) 作战实际限制,飞机数量只能为0或正整数,且实际毁伤的地面目标数量不超过原有目标数量:
Xlk、Yij=0,1,2,…
(12)
以上并未将作战目标约束全部列举,需要根据实际情况制定,约束条件也可以并列使用,如可以同时约定对单个或整体目标造成不少于特定程度毁伤的情况下,出动兵力最少。或者约定在达到特定毁伤程度的前提下,战损最少,等等。
3 实例分析
预攻击的蓝方地面目标群基本情况如表1所示。
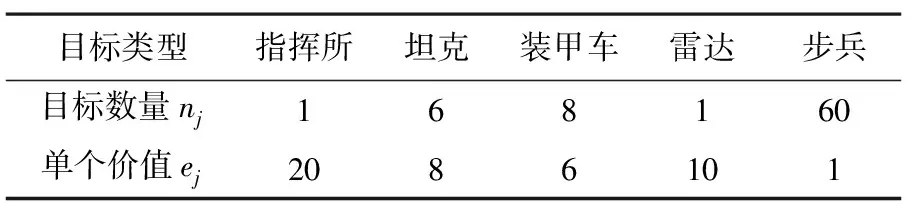
表1 蓝方地面目标群基本情况
红方突击兵力有3种挂载方案,毁伤能力系数如表2所示。
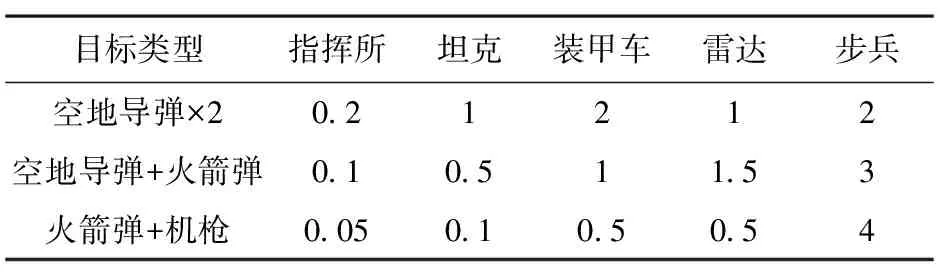
表2 红方突击兵力毁伤能力系数Cij
蓝方防御兵力及拦截能力系数如表3所示。
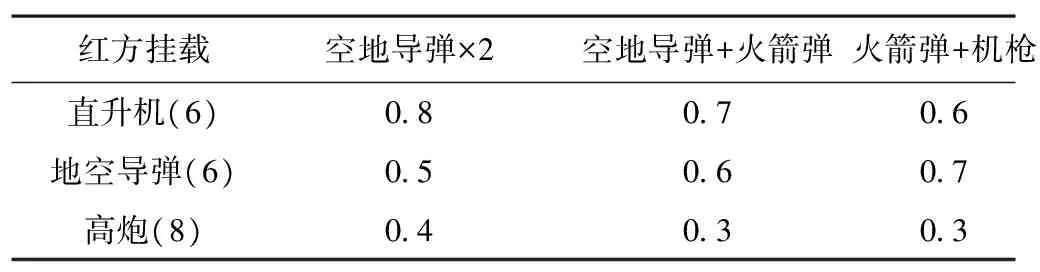
表3 蓝方防线兵力fk及拦截能力系数Hki
红方压制兵力有3种挂载方案,压制能力系数如表4所示。
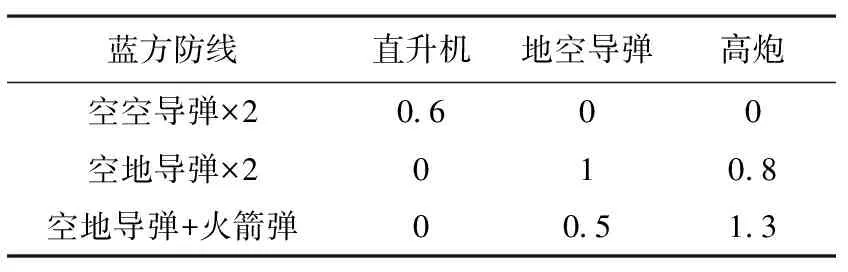
表4 红方压制兵力压制能力系数Ilk
情况一:出动最少兵力,在摧毁蓝方地面指挥所的前提下(毁伤程度超过80%),对目标群总毁伤不低于60%,模型表示为
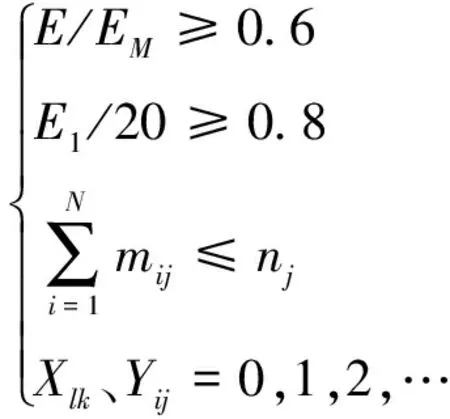
(13)
该模型为非线性整数规划模型,使用LINGO仿真解算[7-8],需要出动飞机38架,突击兵力战损1.5架,最大毁伤效能121.81,具体兵力分配以及挂载方案如表5所示。
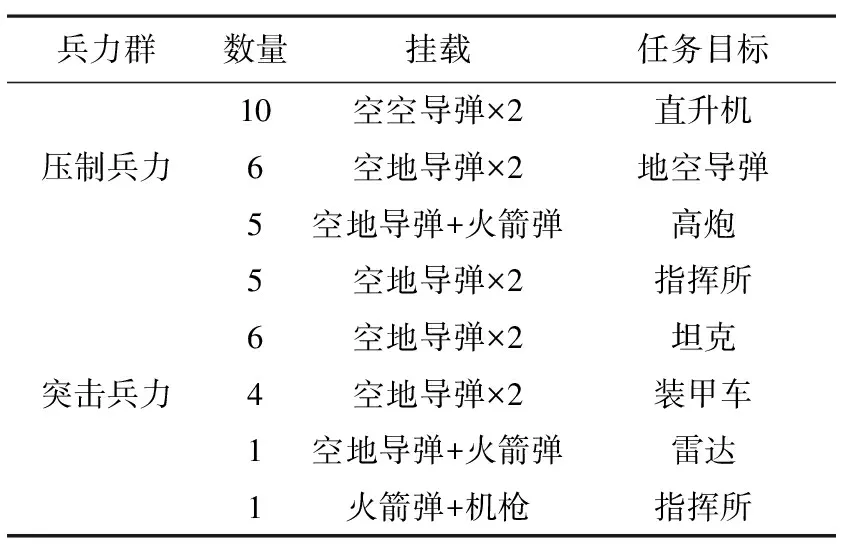
表5 情况一兵力需求
情况二:出动最少兵力,对目标群总毁伤不低于50%,且突击兵力战损小于1架,即
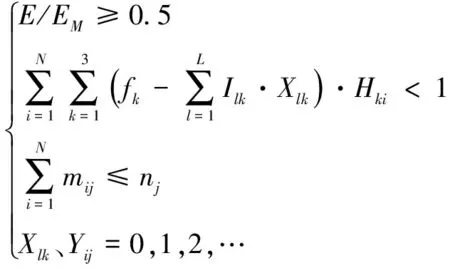
(14)
可以解算出,需要使用兵力33架,突击兵力战损0.2架,最大毁伤效能96.72,兵力分配以及挂载方案如表6所示。
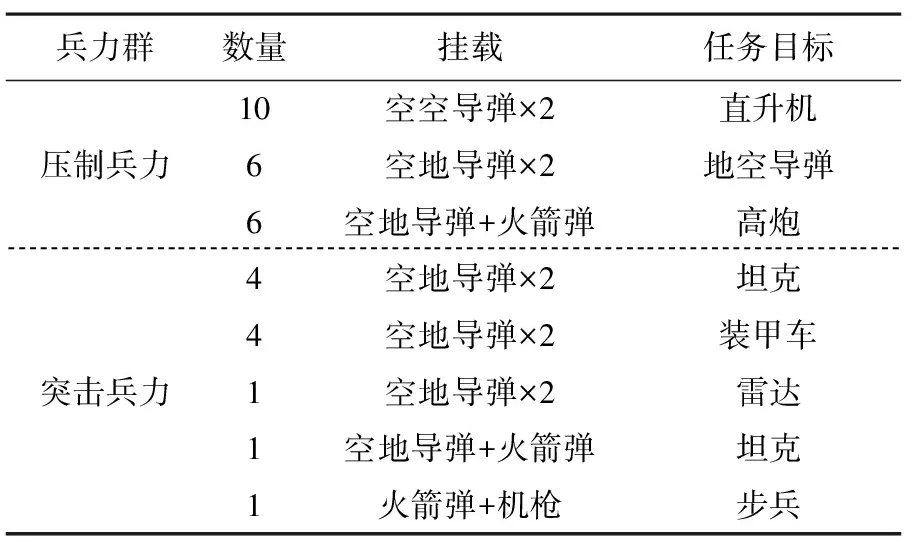
表6 情况二兵力需求
对比表5、表6可知,压制兵力由21架增加到22架,突击兵力可减少损失1.3架;突击兵力由11架增加到17架,最大毁伤效能可以提高25.09。指挥员可根据不同作战目标,本着“保存自己,消灭敌人”的原则派遣兵力。武器挂载方面,使用空空导弹压制对方直升机群,空地导弹打击地面装甲和工事类目标,火箭弹和机枪打击非装甲类目标和有生力量。结果符合作战常识以及各类武器的使用特点,也证明了模型的合理性。
4 结束语
本文针对作战实际,以目标群基本属性以及防御方3道防线为基础,考虑不同弹药挂载方案对任务的影响,建立了规范交战方式下武装直升机编队对地攻击毁伤效能与兵力需求之间的关系模型,并通过约束限制,解算出不同作战情况下编队的兵力需求、任务分配以及挂载方案。通过实例表明,该模型准确规范,高效稳定,便于仿真实现,为武装直升机对地攻击兵力需求预测提供了科学的理论依据,满足了编队指挥员和决策者的需要,具有较大的理论价值和实际意义。
[1] 王三喜, 俞杰, 夏新民. 联合火力打击弹药需求计算动态模型研究[J]. 火力与指挥控制, 2009, 34(10): 100-102,107.
[2] 包强, 张庆捷, 刘阳, 等. 突袭敌方指挥所兵力需求仿真[J]. 火力与指挥控制,2009, 34(11): 95-97.
[3] 梁宇, 李勇, 尤志锋, 等. 摧毁固定目标的空袭兵器需求量算法研究[J]. 现代防御技术, 2006, 34(5): 19-22.
[4] 张毅, 陈正. 基于规范交战方式和Lanchester方程的对地攻击兵力需求分析[J]. 海军航空工程学院学报, 2012, 27(5): 593-596.
[5] 郭浩波, 王颖龙. 兵力需求系统动力学模型研究[J]. 海军工程大学学报, 2006, 18(5): 83-86,90.
[6] 万路军, 姚佩阳, 王欣, 等. 航空兵火力突击兵力需求分析与建模[J]. 火力与指挥控制, 2011, 36(11): 51-55,59.
[7] 司守奎, 孙玺菁. 数学建模算法与应用[M]. 第2版. 北京: 国防工业出版社, 2016: 11-17.
[8] 谢金星, 薛毅. 优化建模与LINDO/LINGO软件[M]. 北京:清华大学出版社, 2005: 84.
Investigation on the Demand for Armed Attack Forceof Armed Helicopter Formation
MIAO Li-da, WANG Zong-jie, SUN Shou-fu
(Naval Aeronautical and Astronautical University, Yantai 264001, China)
In order to solve the problem of force combat demand, we can describe the performance characteristics of the airborne weapon system, and describe the influence of the change of the armed forces with different combat missions on the combat results. Build the model of helicopter formation force demand calculation, combined with operational requirements, the solution of the optimal armed groups and mount programs. The results of case verification show that the model is efficient and credible, and can provide scientific theoretical basis for the prediction of formation force attack.
armed helicopter; formation; force; demand; distribution
2017-03-20
苗李达(1981-),男,辽宁锦州人,硕士研究生,研究方向为航空兵作战运用。 王宗杰(1978-),男,硕士,讲师。 孙守福(1981-),男,博士研究生。
1673-3819(2017)03-0016-03
E834
A
10.3969/j.issn.1673-3819.2017.03.004
修回日期: 2017-03-30

