有序样本聚类方法在城市轨道交通运营时段划分中的应用
曾小旭,汪林,罗贤迪,张宁,赵圣娜
有序样本聚类方法在城市轨道交通运营时段划分中的应用
曾小旭1,汪林2,4,罗贤迪3,张宁2,赵圣娜2
(1.天津市地下铁道运营有限公司,天津300222;2.东南大学ITS研究中心轨道交通研究所,南京210018; 3.东南大学成贤学院,南京210088;4.北京城建设计发展集团股份有限公司,北京100045)
为合理划分轨道交通运营时段并指导其开行方案,提出一种基于有序样本聚类技术的运营时段划分方法。根据统计时段内客流数据,引入单向OD(origin-destination)概率矩阵,并给出单向OD概率矩阵的时序模型和提取方法;利用有序样本聚类方法,以最优分割法量化站间客流转移规律,求解聚类方案。最后以某一轨道交通线路为例,提取时间间隔为20 min的上行OD概率矩阵时间序列,以最优分割法进行聚类,将站间客流转移规律相近的统计时段归为一类,提出目标线路运营时段划分方案。
城市轨道交通;单向OD概率矩阵;运营时段划分;有序样本聚类
城市轨道交通列车开行方案规定了列车在沿线各车站的到发时刻,是日常运营组织的前提与基础[1]。为最小化站台乘客的候车时间,提高服务水平,运营单位广泛采用分时段等间隔发车的列车开行方案[2]。这种方案具体表现为:客流高峰期缩短发车间隔,以提高发车频率的方式减少乘客候车时间;客流低谷期延长发车间隔,通过减少发车次数以节约运营成本。
常见的运营时段划分方法是根据一日内目标线路特征区间断面客流的变化情况,将运营日全天划分为高峰时段、正常时段、低谷时段、过渡时段等若干运营时段[3],不同运营时段的客流规律通常存在较大差异。鉴于断面客流数据无法直接由乘客交易记录统计[4],本文基于目标线路特定时间间隔的单向OD矩阵,提取相对应的单向OD概率矩阵,并对提取的矩阵序列进行有序样本聚类分析,以期实现运营时段的合理划分,为优化列车开行方案提供依据。
1 目标线路单向OD概率矩阵
1.1 目标线路单向OD矩阵
轨道交通OD矩阵反映了线路上起、讫点之间的乘客出行分布[5],体现了乘客在矩阵包含的起、讫点之间的出行需求。目标线路OD矩阵包括上行和下行两个客流统计方向,本文以上行方向单向OD矩阵为例进行分析。
将目标线路共J个站点依次编号为1,2,…,J,在统计时段Tk内抵达目标线路站点i候车,且选择站点j下车的乘客人数记作以自动售检票(automatic fare collection,AFC)系统采集的历史交易记录作为基础数据,对Tk时段内各进行统计。在客流需求给定的前提下,各站首班车离站前抵达候车的乘客,其当前出行不受发车方案的影响。
因此,本文仅针对首班车离站后的站台候车人数进行统计,可得目标线路对应时段的单向OD矩阵Sk,且有(Sk)ij=
1.2 目标线路单向OD概率矩阵
1.2.1 单向OD概率矩阵的时序模型
单向OD概率矩阵反映了目标线路上乘客在各起、讫点之间的出行分布概率。将统计时段Tk内抵达站点i候车的乘客在站点j下车的概率记作由于仅考虑上行客流,故有<J)。因此,在统计时段Tk内,目标线路单向OD概率矩阵Ak为J×J上三角阵,且有(Ak)ij=akij,Ak表达式为
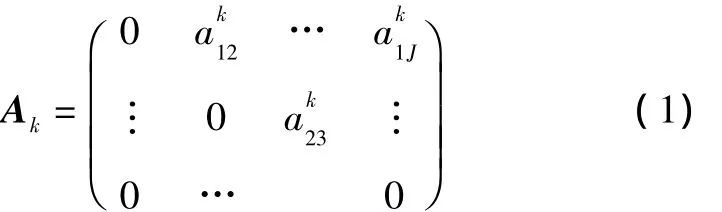
选取适当的时间间隔,将运营日全天划分为若干前后相继的统计时段,并分别对各单向OD概率矩阵进行提取,得到一组时间序列A:{A1,A2,A3,…},该序列反映了目标线路单向OD概率随时间推移的演变情况。
1.2.2 单向OD概率矩阵的提取方法

由伯努利大数定律[6]可知:фε>0,有依概率收敛于当统计时段内抵达站点i候车的乘客数量足够多时,“乘客选择站点j下车”这一随机事件发生的频率与相应概率的偏差大于预先给定精度ε的可能性会小到忽略不计。因此,可构建矩阵Bk对Ak进行估计,使得当几乎不存在较大偏差,Bk表达式为

当在统计时段内抵达目标线路站点i候车的上行方向乘客数给定时,可借助契比雪夫不等式[6]估计上述方法的可靠性,表达式为

由于工作日与周末属于不同类运营日,其群体出行规律存在较大差异[7]。因此,在提取单向OD矩阵时,通过增大统计样本数量,选取多个同类运营日的交易记录,以此来满足预估参数的精度及可靠性要求。
2 有序样本聚类法
2.1 概述
在许多实际问题中,对按一定要求排列的样本进行聚类分析时,必须保证样本的排列顺序不能被随意打乱[8]。为解决这类样本聚类问题,费歇[9]于1958年提出了有序样本聚类方法,又称最优分割法,算法的基本思想在于:以总的分类损失函数作为评判依据,寻找使得类内相似度最大、类间差异最显著的最优聚类方案。
2.2 原理
2.2.1 类直径定义
设S1,S2,…,Sn是n个有序样本,Si(i=1,2,…n)为m维行向量。设其中某一类G包含的样本为

式中,类直径D( i,j)表示样本的离差平方和;S=
定义该类直径为
2.2.2 分类损失函数定义
用b(n,k)表示将n个有序样本分为k类的某一种分法,记该分法为

式中,1=j1<j2<…<jk<n=jk+1-1为分类点。
该分类法下的损失函数定义为:

当n、k固定时,L b(n,[k])越小,表示各类的离差平方和越小,分类越合理[10],故要寻找一种分类方法P (n,k),使分类损失函数达到最小,P(n,k)即为给定分类数k下的最优分割方法。
2.2.3 最小分类损失矩阵及分类标记矩阵构建
费歇最优分割算法的核心是以下两个递推公式:
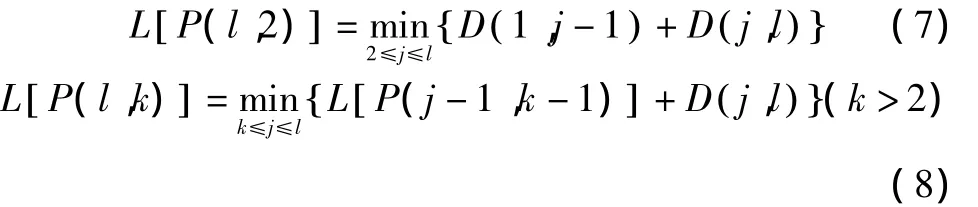
式中,3≤l≤n,k≤j≤n。公式(7)(8)表明,将n个样品分为k类的最优分割方案,建立在使前j-1个有序样本分为k-1类的最优分割之上。
基于上式可得最小分类损失矩阵Pn×n,使得2≤k<l≤n,有(P)lk=L P(l,k[]),矩阵P中其余元素均置为0。
同样可得与之对应的分类标记矩阵Jn×n,使得2≤k<l≤n,有(J)lk=jlk,其中jlk表示P l,(k)中第k类的起始样本序号;且k=l,有(J)lk=k,矩阵Jn×n中其余元素均置为0。
2.2.4 最优分割方案求解
基于最小分类损失矩阵Pn×n以及对应的分类标记矩阵Jn×n,求解最优分割方案P n,(k)。
1)指定分类数k(1<k<n)。(P)nk为最优分类p n,()k对应的最小损失函数,(J)nk为P n,()k中第k类的起始样本序列号jk,满足下式:


可得第k-1类Gk-1={jk-1,jk-1+1,…,jk-1}。以此类推,得到所有分类G1,G2,…,Gk,即为所求的最优分割P(n,K)={G1,G2,…,Gk}。
2)未指定分类数k。若事先不能确定分类数k,则可以作出(P)nk随k变化的趋势图,结合实际应用需求,根据曲线走势确定合适的分类数目。
3 实例分析
3.1 历史数据统计
选取某城市轨道交通2013年3月18日—4月14日所有工作日的线网交易记录作为基础数据,从中提取时间间隔为20min的某线路上行OD概率矩阵序列。该目标线路共有车站26座,运营日按提取时间间隔可划分为54个时间段,即54个有序样本,按时间顺序将样本组织成26×26×54的三维数组,记作OD_RATE。
3.2 有序样本聚类分析
由于单向OD概率矩阵序列具有明显的时序特性,利用最优分割法对OD_RATE进行初次聚类,得到分类损失函数L[ p( 54,k)]随分类数k的变化趋势,如图1所示。
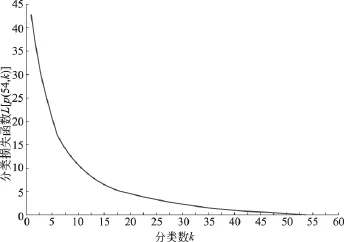
图1 基于最优分割的初次聚类损失函数变化趋势Fig.1 Trend of first clustering loss function based on optimal separation
当分类数k<10时,曲线较为陡峭;当k>15时,曲线渐趋平缓,损失函数随分类数的增加而缓慢衰减。曲线的拐点大致出现在k=12处,因此,初始分类数设定为12,相应损失函数L[ p( 54,12)]=8.6873,初次聚类结果如表1所示。
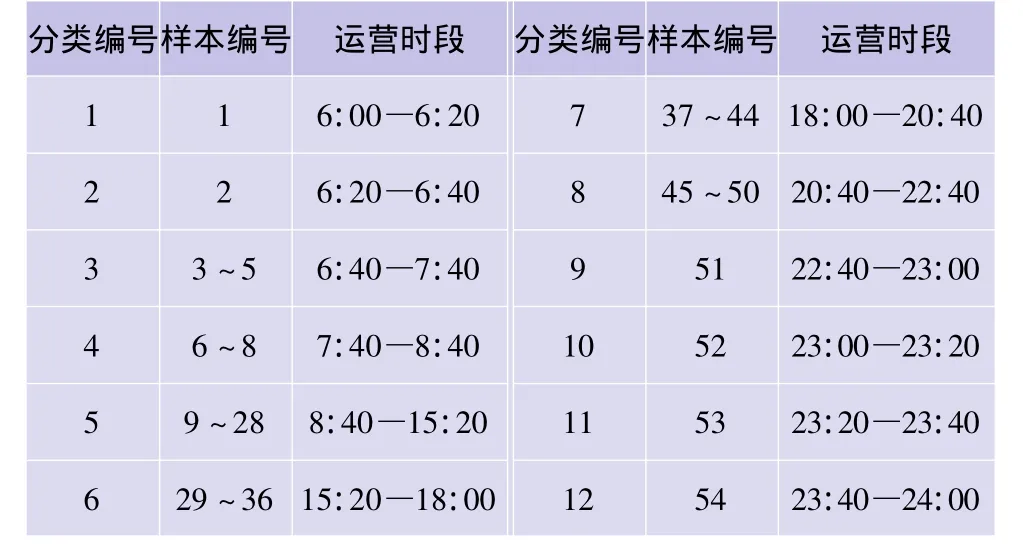
表1 初次聚类结果明细Tab.1 Detailed results of first clusterin g
由表1可知,初次聚类结果中存在样本编号为1、2、51、52、53、54的多个孤立点。通过分析相应样本发现,除样本51外的孤立样本点中均出现全零行,样本1、2中的全零行均出现在矩阵下方,行数递减;样本52~54中的全零行均位于矩阵上方,行数单调递增。
结合单向OD概率矩阵的提取方法可推知,样本1、2中的全零行是由构造单向OD矩阵时所采取的客流统计方法造成的。在6:00—6:20时段,由于仅对各站首车离站后的进站客流进行统计,对于首车离站时间在6:20以后的站点,其进站客流均未计入该时段的单向OD矩阵,从而导致样本1中的对应位置出现全零行。同理,样本2中出现全零行。
目标线路运营方式是导致样本52~54孤立的主要成因。在23:00—23:20时段,首站已不再产生有效的进站客流,因此,样本52中首行出现全零;在23:20—23:40时段,对于末班离站时间在23:20以前的站点,亦不再产生有效的进站客流,导致样本53中对应位置出现全零行;样本54中的全零行也是由此导致,且其行数因时间推移而有所增加。
基于上述分析,判定样本1、2、52~54为异常样本,将其从样本集OD_RATE中剔除。对剩余样本进行二次聚类,得到二次聚类的损失函数L[ p( 49,k)]随分类数k的变化趋势,如图2所示。
经分析,曲线的拐点大致出现在k=7处,设定二次聚类的分类数为7,相应损失函数L[ p( 49,7)]= 8.6873,聚类结果如表2所示。

图2 基于最优分割的二次聚类损失函数变化趋势Fig.2 Trend of twice clustering loss funtion based on optimal separation

表2 二次聚类结果明细Tab.2 Detailed results of tw ice clustering
3.3 运营时段划分
依据该城市轨道交通运营管理规定,目标线路上行方向首班发车时间为6:00,末班发车时间为23:00,全程运行时长为58 min。基于上文聚类结果,结合实际运营条件,提出目标线路工作日运营时段划分方案,如表3所示。

表3 工作日运营时段划分方案Tab.3 Division of operation periods ofworking day
在此运营时段划分方案中,全天运营时间被划分为8个不等间隔的运营时段,每个运营时段内的客流分布规律较为统一,不同时段之间则体现出较大的差异性。基于此,轨道交通运营管理部门可根据各运营时段的实际客流情况,选取各自合适的发车间隔,构建目标线路的全日分时段等间隔发车方案并制定相应的列车开行计划。
需要指出的是,该线路末班车发车时间为23:00,末班车到达终点站时间约为23:58,线路全天实际运营时间为6:00—23:58,比有效发车时间6:00—23:00长1 h左右,因此,本方案划分的最后一个运营时段与其实际发车时段并不完全重合。由于末班车于23:00准点发车,故该运营时段的有效发车时间仅为22:40—23:00共计20 min。
4 结语
围绕轨道交通运营时段划分展开研究,提出一种基于有序样本聚类技术的运营时段划分方法,以一定时间间隔内目标线路单向OD概率矩阵为样本,构造有序样本序列,并利用有序样本聚类的最优分割法,量化站间客流转移规律的差异性,在此基础上合理划分运营时段。轨道交通运营时段划分方法的研究,为运营部门制定分时发车计划提供决策支持,同时,也为进一步优化目标线路的运营调度方案奠定基础。考虑到将来轨道交通线网逐渐形成,客流情况更加复杂,需在本研究的基础上着眼于轨道交通全网,兼顾上下行两个方向,增加换乘站等影响因素,这也是作者下一步研究的重点。
[1]牛惠民,陈明明,张明辉.城市轨道交通列车开行方案的优化理论及方法[J].中国铁道科学,2011,32(4):128- 133.
NIU Huim in,CHEN M ingming,ZHANG Minghui.Optim ization theory and method of train operation scheme for urban rail transit[J].China railway science.2011,32(4): 128- 133.
[2]毛保华.城市轨道交通系统运营管理[M].北京:人民交通出版社,2006.
MAO Baohua.Operation and management for urban rail transit[M].Beijing:China Communications Press,2006.
[3]孙焰,施其洲,赵源,等.城市轨道交通列车开行方案的确定[J].同济大学学报(自然科学版),2004,32(8): 1005- 1008.
SUN Yan,SHIQizhou,ZHAO Yuan,et al.Method on making train running-plan for urban railway traffic[J].Journal of Tongji University(natural science edition),2004,32(8):1005- 1008.
[4]Newell G F.Dispatching policies for a transportation route[J].Transportation science,1971,5(1):91 105.
[5]徐瑞华,徐永实.城市轨道交通线路客流分布的实时预测方法[J].同济大学学报(自然科学版),2011,39(6):857 861.
XU Ruihua,XU Yongshi.Real-time forecastof passenger flow distribution on urban rail transit line[J].Journal of Tongji University(natural science edition),2011,39(6):857 861.
[6]王红,刘磊.概率论与数理统计[M].上海:同济大学出版社,2014.
WANG Hong,LIU Lei.Probability and mathematical statistics[M].Shanghai:Tongji University Press,2014.
[7]邱华瑞.城市轨道交通客流时空演变规律研究[D].南京:东南大学,2014.
QIU Huarui.Research of passenger flow space-time evolution regularity on urban rail transit[D].Nanjing:Southeast University,2014.
[8]方开泰.有序样品的一些聚类方法[J].应用数学学报,1982,5(1):94- 101.
FANG Kaitai.Some clustering methods for the order sample[J].Actamathematicae applicatae sinica,1982,5(1): 94- 101.
[9]FISHER W D.On grouping for maximum homogeneity[J].Journal of the American statistical association,2015,53(284):789- 798.
[10]周东华.数据挖掘中聚类分析的研究与应用[D].天津:天津大学,2006.
ZHOU Donghua.Research and application of cluster analysis in datamining[D].Tianjin:Tianjin University,2006.
(编辑:曹雪明)
Application of Ordinal Clustering in the Division of Operation Periods for Urban Rail Transit
ZENG Xiaoxu1,WANG Lin2,4,LUO Xiandi3,ZHANG Ning2,ZHAO Shengna2
(1.Tianjin Metro Operation Co.,Ltd.,Tianjing 300222;2.ITSRail Transit Research Institute of Southeast University,Nanjing,210018;3.Scool of Chengxian,Southeast University,Nanjing 210088; 4.Beijing Urban Construction Design&Development Group Co.,Ltd.,Beijing 100045)
To divide rail transit operation period reasonably and conduct the operation plan,amethod of operation period division using ordinal clustering was put forward in this paper.On the basis of one-way OD(Origin-Destination)probability matrix,the timingmodel and extractionmethod for one-way OD probabilitymatrix in a statistical period was given.Then,the optimal partition algorithm was used to quantify interstation-passenger-transfer rules and solve the ordinal clustering scheme.Finally,the time sequences of uplink OD probabilitymatrix(for an interval of 20m inutes)was constructed on the case of a rail transit line.According to the results of the ordinal clustering by the optimal partition algorithm,the statistical periods with similar interstation-passenger-transfer rules were classified together and the operation period division was proposed,providing decisionmaking basis for division of operation periods by the operation department.
urban rail transit;one-way OD probabilitymatrix;division of operation periods;ordinal clustering
F530.7
A
1672- 6073(2017)02- 0108- 05
10.3969/j.issn.1672 6073.2017.02.022
2016- 05 27
2017 01 08
曾小旭,男,高级工程师,从事轨道交通运营管理、调度指挥等工作,18530606@qq.com
交通运输部建设科技项目(2015318J33080);江苏省重点研发计划(社会发展)项目(BE2016740)

