平面向量在解答证明题中的应用

徐凡顺

【摘 要】随着新课程改革的不断深入，高中数学知识中的很多知识点都被列入重点学习范围，其中向量的应用是我们在高中数学学习过程中必须掌握的重要内容。我们在学习高中数学的过程中可以发现，向量在很多题型中都可以被应用，其可以使得很多复杂的数学题得到简化，因此，我们在解答部分题型的过程中就经常会想到利用向量解决问题。高中数学有一种题型是具有较强的综合性和多样性的，这就是证明题。我主要结合自己的学习经驗对平面向量在解答证明题中的应用进行简要的分析，希望对同学们学习相关知识有一定的帮助。

【关键词】平面向量；证明题

我们在学习高中数学的过程中，需要对不同的知识内容进行不同程度的理解和应用，这是高中数学的特点，也是其难点所在。就高中数学中的证明题来说，我们应用哪种方法进行证明，就取决于我们对高中数学知识点的认识。我在解答证明题的过程中发现很多同学会应用传统的证明方法完成整个证明过程，但是很多时候传统的方法比较复杂，在应用这样的方法解答证明题的过程中无疑就给数学题增大了一定的难度，而平面向量则可以使得证明过程得到一定的简化，这对于提升我们的解题效率来说，具有较大的作用。

一、勾股定理

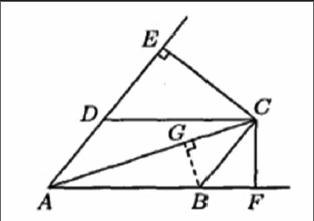
我们在初中的时候就学习了勾股定理这一数学理论，这是在解决三角形问题中最常用的方法，而在很多应用平面向量对题干进行证明的数学题中，经常是以三角形的形式出现，因此，我们就可以根据题意观察是否可以使用勾股定理进行解题。平面向量的运算本身就能够将很多几何关系转化为代数运算，这在勾股定理中的体现是很明显的。比如：已知平面四边形ABCD，AC是其中较长的一条对角线，过点C分别做AD、AB延长线的垂线，垂足为E、F，证明|AB|·|AF|+|AD|·|AE|=|AC|2。

在解答这个题的时候，我们是可以应用传统的证明方式对其进行解答的，就是如上图，做一条辅助线，使得BG⊥AC，垂足为点G，然后结合三角形的相似性和勾股定理进行解答，但是这种方式在解答过程中会显得比较繁琐，很多线段长度之间的关系比较复杂。我主要用平面向量的解答方式进行分析：我们可以结合题意和图形知道→CF⊥→AF，→CE⊥→AE，这样就可以得到→CF⊥·AF=→CE·→AE=0，又因为→AB与→AF的方向相同，因此|AB|·|AF|=→AB·→AF。同理可以得到|AD|·|AE|=→AD·→AE，这样的话，就可以列出一个等式为→AB·→AF +→AD ·→AE=→AB·（→AC+→CF）+→AD·（→AC+→CE）=→AB·→AC+→AD·→AC=→AC·→AC，因此就可以得到|AB|·|AF|+|AD|·|AE|=|AC|2。通过这个题的解答我们可以知道应用平面向量的方法解答证明题相对于传统的方法来说更加简单明了，不需要添加辅助线和拆分相关的量，从而使得我们的解答过程更加简便，并且理解起来也不必那么费劲。

二、三角形三高交于一点

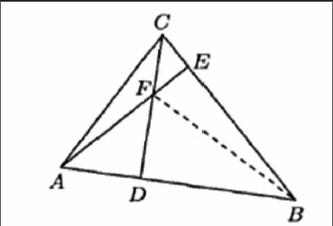
在用平面向量解答证明题的过程中，它并不会局限于平面几何问题中，其在立体几何中也具有良好的应用作用。立体几何是我们在学习高中数学的过程中，经常会碰到的一类题型，也是高中数学中的重点和难点，应用平面向量对这类证明题进行解答，能够使得立体几何问题进行转化，从而降低解题难度。比如：在△ABC中，AE、CD分别为BC、AB边上的高，并且AE、CD相交于一点F，在图中连结BF，证明，图中三条连线相交于一点。

在证明过程中我们首先就可以由三角形的定理得知BF的延长线就是AC边上的高，但是这需要我们的证明，而传统的证明方法对这个题来说有一定的难度，因此就可以用平面向量的方式进行解题。我们可以由已知得到→AF·→BC=0，→CF·→AB=0，因为→AB+→BC+→CA=→0，所以可以得到→BF·→CA=（→AF-→AB）·（→CF-→AF）=→AF·→CA+→AB·→AF=→AF·（→CA+→AB）=→AF·（-→BC）=0，所以就可以由向量关系得出→BF⊥→AC，因此，就可以得到AC边上的高是过BF的线段，所以三条线段是相交于一点的，并且交点为点F。

三、相似性

相似性是三角形最基本的性质，这个性质在其他的平面图形中也是通用的，我们在应用向量进行数乘运算的时候，可以说相似性正是其来源。在解答多边形相关问题的过程中，运用平面向量进行解题就是的向量形成了数乘运算分配率。因此，在解答关于图形的相似问题的证明题的时候，运用平面向量进行解题就是验证向量的基础运算法则。我们在应用平面向量解答很多几何证明题的过程中，经常需要用到相似性定理，可以说，这是解答几何证明题的基础，同时也是属于通用性质的。相似性定理在平面向量解答证明题的过程中是起到桥梁作用的，对于整个证明过程有比较重要的作用。

四、结语

综上所述，在应用平面向量解答证明题的过程中，可以使得证明过程得到一定的简化，而不需要像传统的证明方式那样繁琐。当我们在解答几何证明题的时候，通常首先就会想到用向量的方式进行证明，需要注意的是，我们要视具体的情况进行具体分析，灵活运用平面向量和几何数量之间的关系，最大程度地提升我们的数学理解能力和运用能力，从而提升我们的综合数学学习能力。

参考文献：

[1]赵小强.平面向量在解题中的应用[J].中学课程辅导：教学研究，2014

[2]李健.平面向量在解题中的应用[J].学周刊，2012