基于模糊Smith控制的智能阀门定位器

张 浩， 王 昕， 王振雷， 智茂轩， 蒋明敬

(1. 华东理工大学 化工过程先进控制和优化技术教育部重点实验室， 上海 200237；2. 上海交通大学 电工与电子技术中心， 上海 200240；3. 中国石油化工股份有限公司 镇海炼化分公司， 浙江 宁波 315207)

·实验技术·

基于模糊Smith控制的智能阀门定位器

张 浩1， 王 昕2， 王振雷1， 智茂轩3， 蒋明敬3

(1. 华东理工大学 化工过程先进控制和优化技术教育部重点实验室， 上海 200237；2. 上海交通大学 电工与电子技术中心， 上海 200240；3. 中国石油化工股份有限公司 镇海炼化分公司， 浙江 宁波 315207)

针对工业调节阀中广泛存在的时滞现象，提出一种基于模糊原理的带有Smith预估器的智能阀门定位器控制方法。分析智能阀门定位器的结构和原理，通过设计Smith预估器补偿滞后时间，实现超前响应，克服时滞对系统性能的影响；通过模糊控制与PID控制结合，设计调整模糊规则，实现控制器参数的自整定。两者结合构成模糊Smith方法，提高了系统的动静态性能。模糊内模控制器对克服时滞、提高系统性能有良好的效果，将模糊Smith器与模糊内模控制器及PID控制器进行仿真研究对比。仿真结果表明，模糊Smith控制方法比模糊内模控制方法和传统PID方法更能有效地提高调节阀的快速性，克服时滞，改善系统性能。

智能阀门定位器； 模糊Smith； 模糊内模； 时滞

0 引 言

调节阀又称控制阀，它是过程控制系统中用动力操作去改变流体流量的装置。调节阀等辅助控制装置能决定工业过程控制的质量，它在一定程度上影响过程控制的调节品质。阀门定位器作为调节阀的核心附件，有重要的控制作用。通过阀门定位器可以更精确地调节流体的流量，这将直接影响控制系统的整体性能[1]。在工业过程中，时滞是常见的影响系统品质的特性之一。在阀门定位器控制流量过程中存在时滞问题，通过改善阀门定位器的控制方法，可以提高系统的快速性，对优化工业过程、降低成本、提高生产效率等有很大的帮助[2]。

相对传统阀门定位器，智能阀门定位器不仅体现出精度提高、能耗降低、功能增多等优点，而且它能结合经典与先进的控制技术，改善控制系统的动、静态性能，满足工业上的要求[3]。文献[4]中将PID控制算法与模糊逻辑控制原理结合起来，形成一种模糊自适应PID控制算法，并与传统的PID控制算法进行对比，该方法在一定程度上提高了系统的快速性。文献[5-6]中将模糊控制算法和模糊自适应策略应用在工业过程控制中，提高了控制系统的稳定性，加快了系统的响应速度。文献[7]中首先提出了内模控制设计方法，并与PID原理相结合，它是现今最常用的控制器设计方法之一。在此基础上，文献[8-9]中将内模PID控制方法与模糊逻辑策略结合到一起，应用到工业过程中，该方法的控制器参数计算简便，便于调节，易于实现，系统既有较好的动态特性，又有较小的超调和较短的过渡时间。在许多工业过程中，系统的动态过程以及反馈环节都存在时滞现象，这会影响控制系统的性能。文献[10]中以一阶时滞系统(FOPDT)为控制对象，提出了基于Smith预估器的控制方案，该方法可有效消除时滞对系统动态性能的影响，加快时滞系统的调节过程。文献[11]中把模糊PID与Smith预估器相结合，控制精度高，自适应能力强，动静态性能有很大提高。

本文将模糊Smith控制方法与模糊内模控制方法应用到流量阀定位器的控制中。对过程进行建模、仿真。结果表明，上述两种方法能显著提高系统的快速性，改善系统的动态性能。其中模糊Smith方法效果更突出。

1 智能阀门定位器

1.1 智能阀门定位器

气动系统具有物理结构简单、成本低、对环境无不良影响等特点，所以气动调节阀逐步成为工业中的一种重要的执行单元。但由于空气介质的自身特点，使控制精度保持在一个较高水平上是当前气动技术的难点。随着微电子技术的迅猛发展，微处理芯片具有更高的集成度，在一块芯片上可以集成CPU、存储器、并行和串行接口等，这也就是单片机。单片机的出现，引起了仪器仪表结构的根本性变革，以单片机为主体取代传统仪器仪表的常规电子线路，可以容易地将计算机技术与测量控制技术结合在一起，组成新一代的所谓“智能化测量控制仪表”[11]。智能阀门定位器使用单片机和阀位传感器，使其具备许多符合现代生产过程技术要求的功能，具有传统阀门定位器不可比拟的优势：它实现了智能化，方便修改控制阀流量特性，工作稳定性好，可以实现诊断及报警，具有更高的可靠性[12]。

1.2 智能阀门定位器工作原理

如图1所示，智能气动阀门定位器采用的是以单片机为核心的控制电路，它接受来自调节器的设定阀门开度的电流信号(4～20 mA)。当阀位开度设定后，定位器根据设定值与阀位变送器的反馈值的偏差来控制进气阀或排气阀动作，通过充气或排气来控制气室压力。气室气体压力通过膜片作用推动阀杆动作，从而实现控制作用。如果偏差很大，则输出连续信号给压电阀；如果偏差很小，则没有定位脉冲输出；如果偏差大小适中，则输出脉冲序列给压电阀，从而使一定量的压缩空气经过压电阀进入到调节阀的执行机构的气室，推动阀芯的移动或转动，从而达到阀芯的准确定位[13]。

图1 智能阀门定位器结构原理

以HA1D型气动调节阀为例，其行程范围为38 mm，阀门特性可以表示为工业中常见的一阶惯性时滞对象[14]。调节阀特性传递函数如下式所示：

(1)

2 控制器原理与设计

2.1 模糊控制

模糊控制是一种由模糊数学、计算机科学、人工智能、知识工程等多门学科领域相互渗透、理论性很强的科学技术，它与传统控制不同，不需要知道控制对象的数学模型，它的组成核心是具有智能性的模糊控制器[15]。

模糊控制的原理主要包括模糊化、模糊推理和清晰化。 把实际测量的物理量通过比例因子转变成其语言变量论域中不同的模糊子集，这就是模糊化。模糊推理则调用数据库，而其输出子集由系统的状态来决定。清晰化是将由模糊推理所得到的模糊控制量转化成所要输出控制量的过程。

2.2 内模PID控制

内模控制结构如图2所示，把内模控制结构等效变换为简单反馈控制形式，将内模控制与PID控制相结合其等效结构如图3所示[16]。

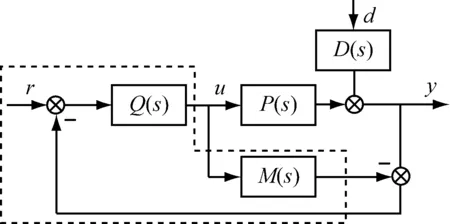
图2 典型内模结构控制图

图3 等效内模结构控制图

设计步骤为：

步骤1M(s)可分解成

(2)

式中：M+(s)包含了所有时滞和、平面零点；M-(s)是具有最小相位特征的传递函数。

步骤2 定义内模控制器为：

(3)

式中：分子为M-(s)的逆，分母为低通滤波器，以确保系统的稳定性和鲁棒性；λ为滤波器参数，是内模控制器仅有的设计参数。对于一阶时滞模型而言，滤波器阶次为1。 因此数学模型为：

(4)

式中：K为过程稳态增益；L为滞后时间；T为过程的时间常数。

用一阶泰勒级数逼近时滞项

(5)

将式(2)～(4)化简，可得反馈控制器为:

(6)

与理想的PID控制器形式相比，得:

(7)

(8)

(9)

2.3 Smith预估器

含有Smith预估器的控制系统结构图如图4所示，图中：Gc(s)为控制器；Gp(s)为不含时滞部分的数学模型；e-τs为时滞部分。

图4 Smith预估器控制图

Smith预估器是针对大时滞系统设计的一种控制算法(见图4)。其原理为：首先得出系统的动态模型，获取模型参数；然后补偿滞后时间使控制器超前响应，从而避免了系统中纯滞后特性。

当模型准确时，通过计算得到Smith预估器传递函数为：

(10)

其特征方程为:

(11)

由式(10)可以得出，在该传递函数中，分母原有的滞后环节e-τs被消除，系统的控制器响应滞后减少，提高了系统的响应速度。

通过分析，Smith预估器可以使系统的可靠性和稳定性增强。

2.4 模糊Smith控制系统

模糊Smith控制系统结构图如图5所示。

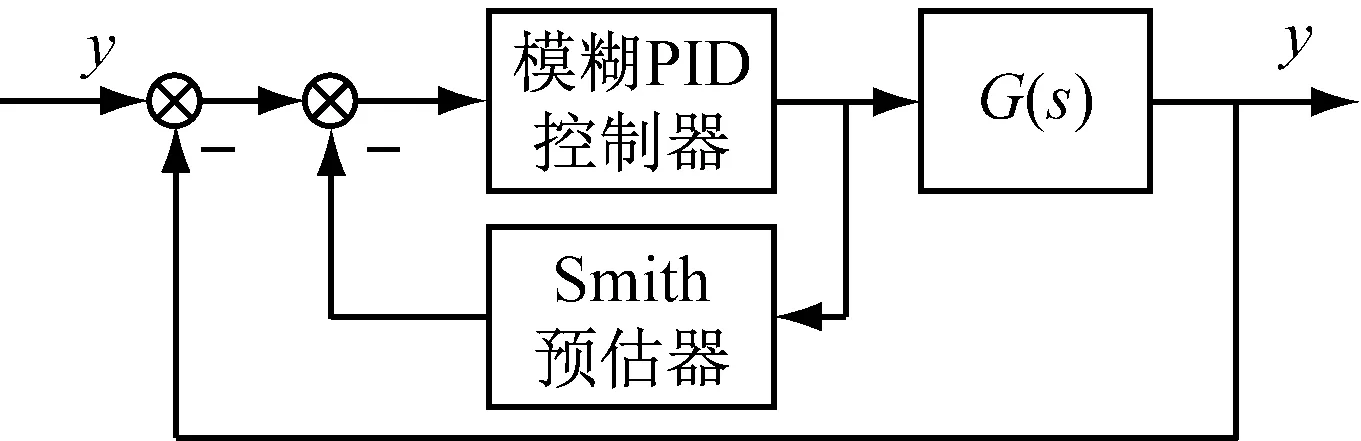
图5 模糊Smith控制图

模糊控制器输入输出参数的模糊子集均为{负大(NB)，负中(NM)，负小(NS) ，零(ZO)，正小(PS)，正中(PM) ，正大(PB)}[14]。其中，E、EC、ΔKp的论域为{-3，-2，-1，0，1，2，3}；ΔKi、ΔKd的论域为{-0.06，-0.04，-0.02，0，0.02，0.04，0.06}。

在所建立的模糊规则中，输出U即3个参数ΔKp、ΔKi、ΔKd。 模糊规则如表1所示。

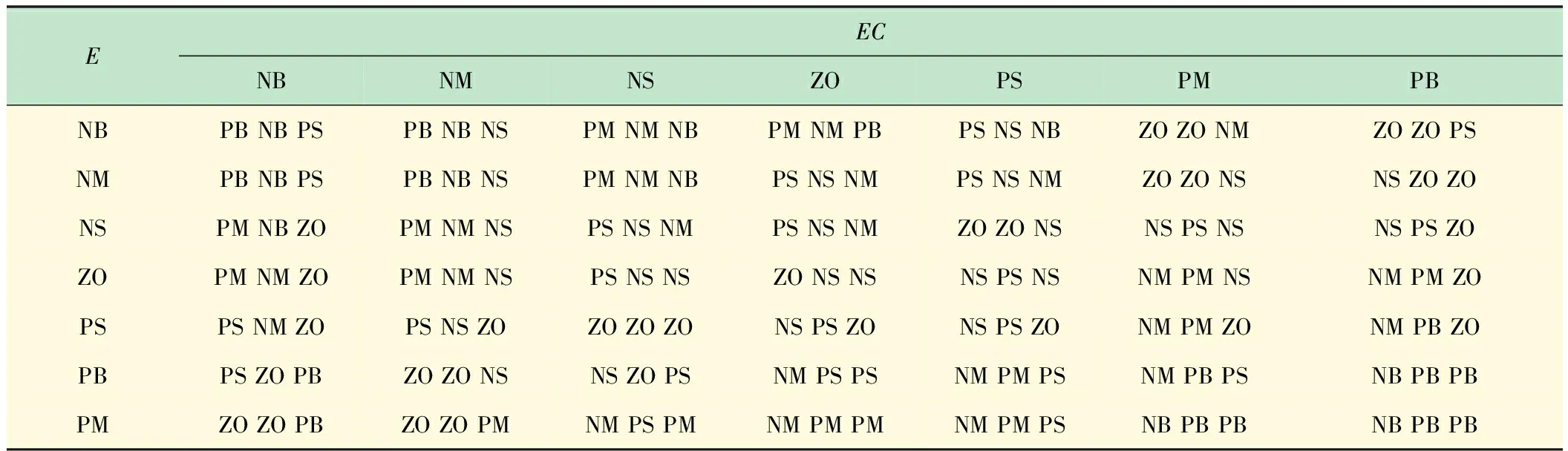
表1 模糊Smith规则表

2.5 模糊内模PID控制系统

建立模糊内模PID控制系统，见图6。图中：C(s)为等效后的反馈控制器；P(s)为被控对象，通过模糊控制器来实现参数λ的修正，修正公式为

图6 模糊内模控制图

在模糊控制器中，E、EC作为模糊控制器的输入，Δλ作为模糊控制器的输出，再由修正公式计算λ，并输出到等效控制器C(s)中，构成PID控制结构，对系统进行控制。

下面对E、EC、U的隶属函数进行说明：各变量均选择三角形的隶属函数，E的模糊子集取{负大(NB)，负中(NM)，负小(NS) ，零负(NZ)，零正(PZ)，正小(PS)，正中(PM) ，正大(PB)} 。液体流量在检测时可能会有所波动，为了保证流量的基本稳定，在误差允许的范围内，允许E有极小的偏差，所以设置E的隶属函数中间疏、两端密。具体结构如图7所示。模糊规则表如表2所示。

图7 E的隶属函数图

EC、Δλ的模糊子集取{负大(NB)，负中(NM)，负小(NS) ，零(ZO)，正小(PS)，正中(PM) ，正大(PB)}，其中EC的论域为{-3，-2，-1，0，1，2，3}，各子集的疏密程度相等。对于输出量Δλ，为了使偏差较大时快速响应，偏差较小时又要提高响应精度和减小超调量，因此设置输出量Δλ的隶属函数时两头疏，中间较密。具体结构如图8所示。

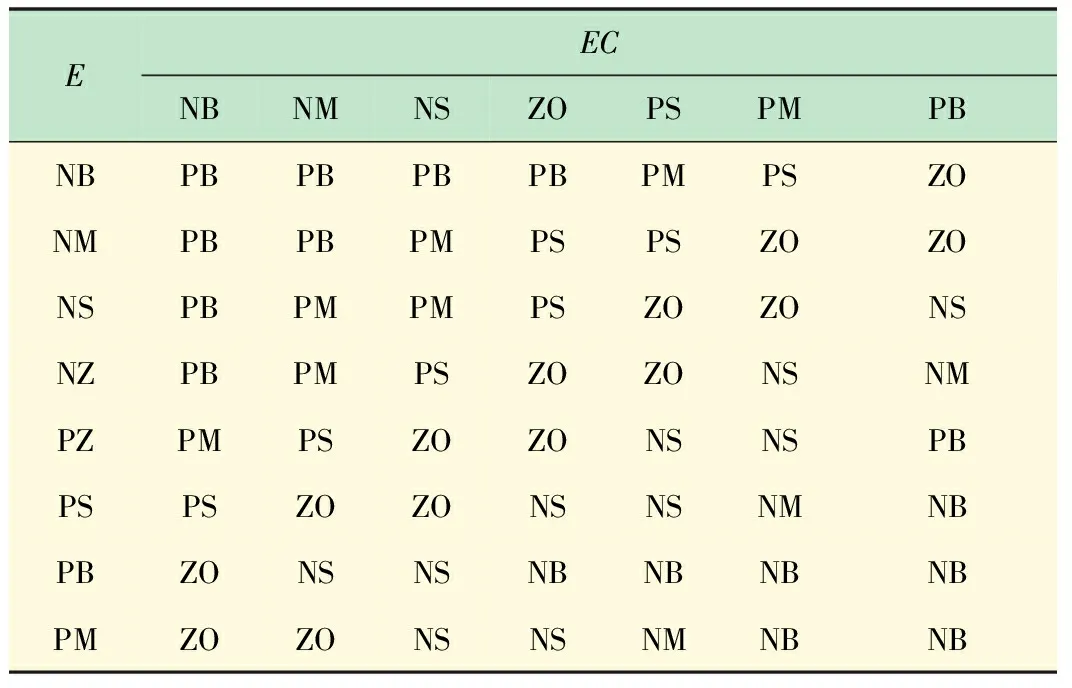
表2 模糊内模规则表

图8 Δλ的隶属函数图

3 仿 真

3.1 模糊Smith控制系统

在模糊Smith控制系统中，通过Smith预估器来克服时滞对系统的影响，通过基于模糊控制器的PID控制方法，使输出快速、有效地反映对输入量的响应。设ΔKp、ΔKi、ΔKd的初始值为0.5，2，0.5。结合模糊控制2个输入量和3个输出量的论域，对比例因子不断调整，当E和EC的输入比例因子分别为40、0.5时，输入量与模糊控制器的论域能有效地联系；当ΔKp、ΔKi、ΔKd的输出比例因子取0.8，0.5，0.5时，输出量能更好地进行PID控制器参数的自整定。考虑到实际对象与模型会有一定的偏差，在构造Smith预估器时，采用如下模型：

(12)

在单位阶跃激励下，响应如图9所示。

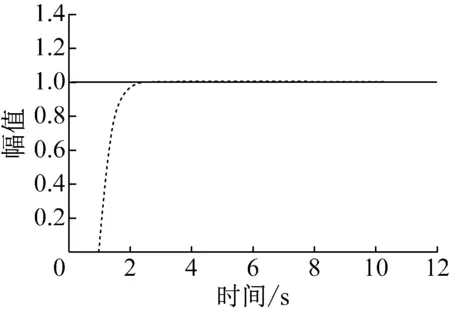
图9 模糊Smith系统阶跃响应图

3.2 模糊内模PID控制系统

在模糊内模控制系统中，将模糊控制器的输出通过修正公式与等效反馈控制器的唯一参数λ相连，再通过这个等效控制器对对象模型进行控制。先取参数初始值λ0=1，对模糊控制器的比例因子进行试凑，当E和EC的输入比例因子为0.1、2且模糊控制器输出比例因子为20时，模糊控制器能产生较好的效果。此时再对参数的初始值λ0进行调整，当初始值λ0为0.2时，控制器效果最佳。

在单位阶跃激励下，其响应如图10所示。

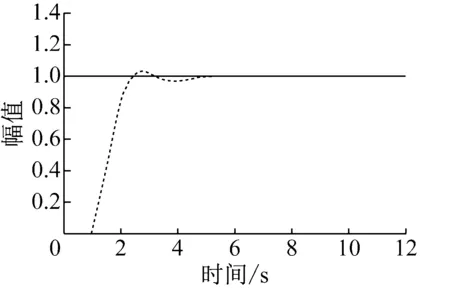
图10 模糊内模系统阶跃响应图

3.3 对两种方法进行分析

取响应曲线上升到0.98时所用的时间作为快速性的指标，记为响应时间。

由图11、图12可得： 模糊Smith方法的响应时间为2.193 s，超调量为0；模糊内模方法的响应时间为2.378 s；超调量为2.8%。 可见，模糊Smith控制方法的响应时间比模糊内模控制方法要少，模糊内模方法会产生超调量，模糊Smith方法不产生超调量。综合快速性和稳定性来看，模糊Smith方法对系统性能的提升更有效。

3.4 3种控制方法比较

将传统PID控制方法、模糊内模控制方法、模糊Smith控制方法一起进行仿真，同时对比一个单位阶跃信号，观察几种方法的阶跃响应，结果如图13所示。

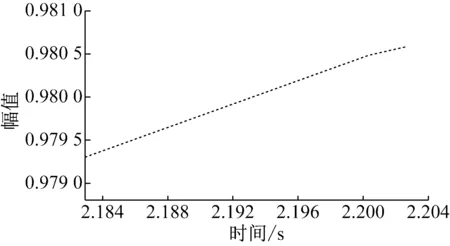
图11 模糊Smith系统阶跃响应细节图

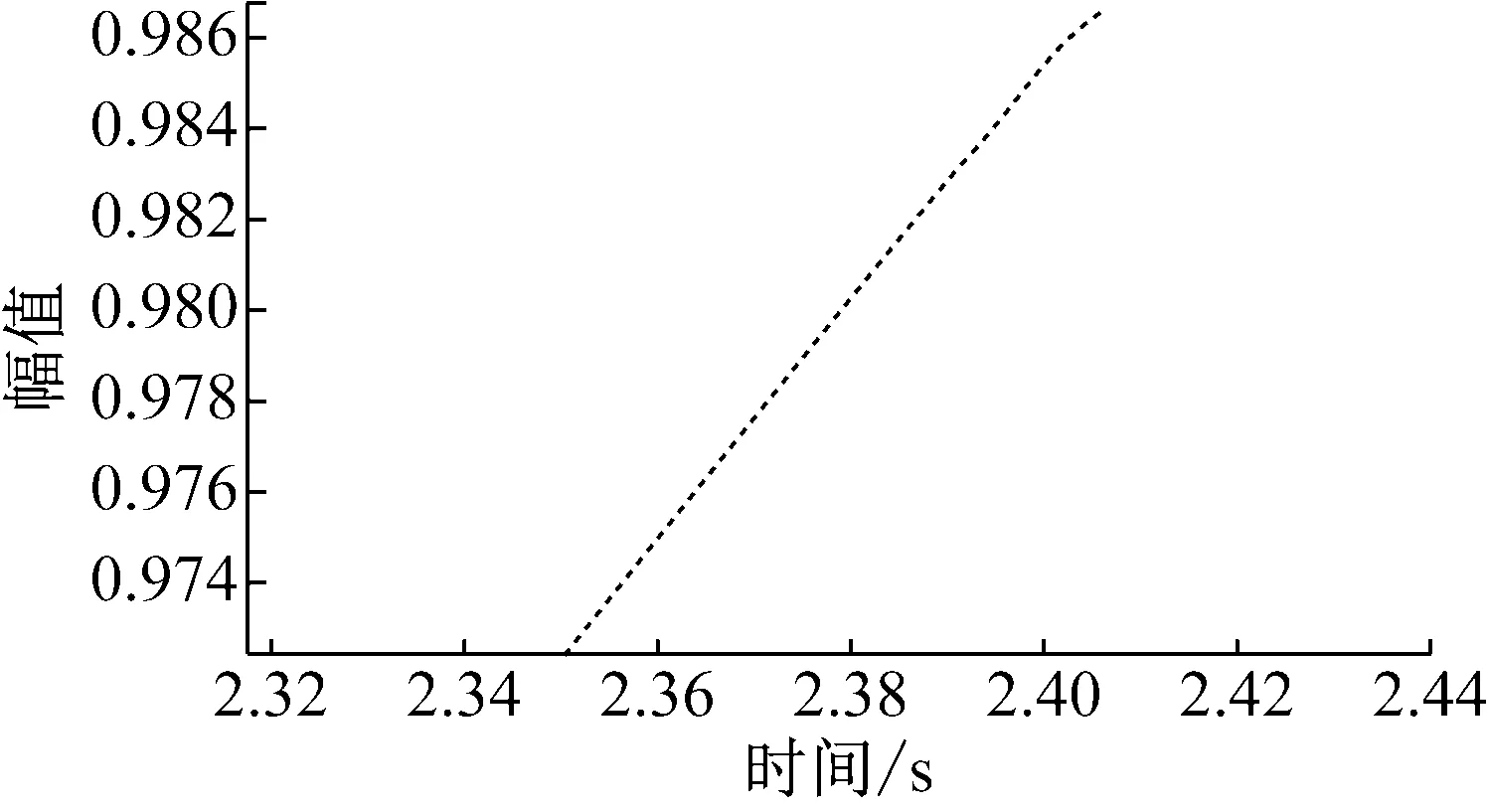
图12 模糊内模系统阶跃响应细节图

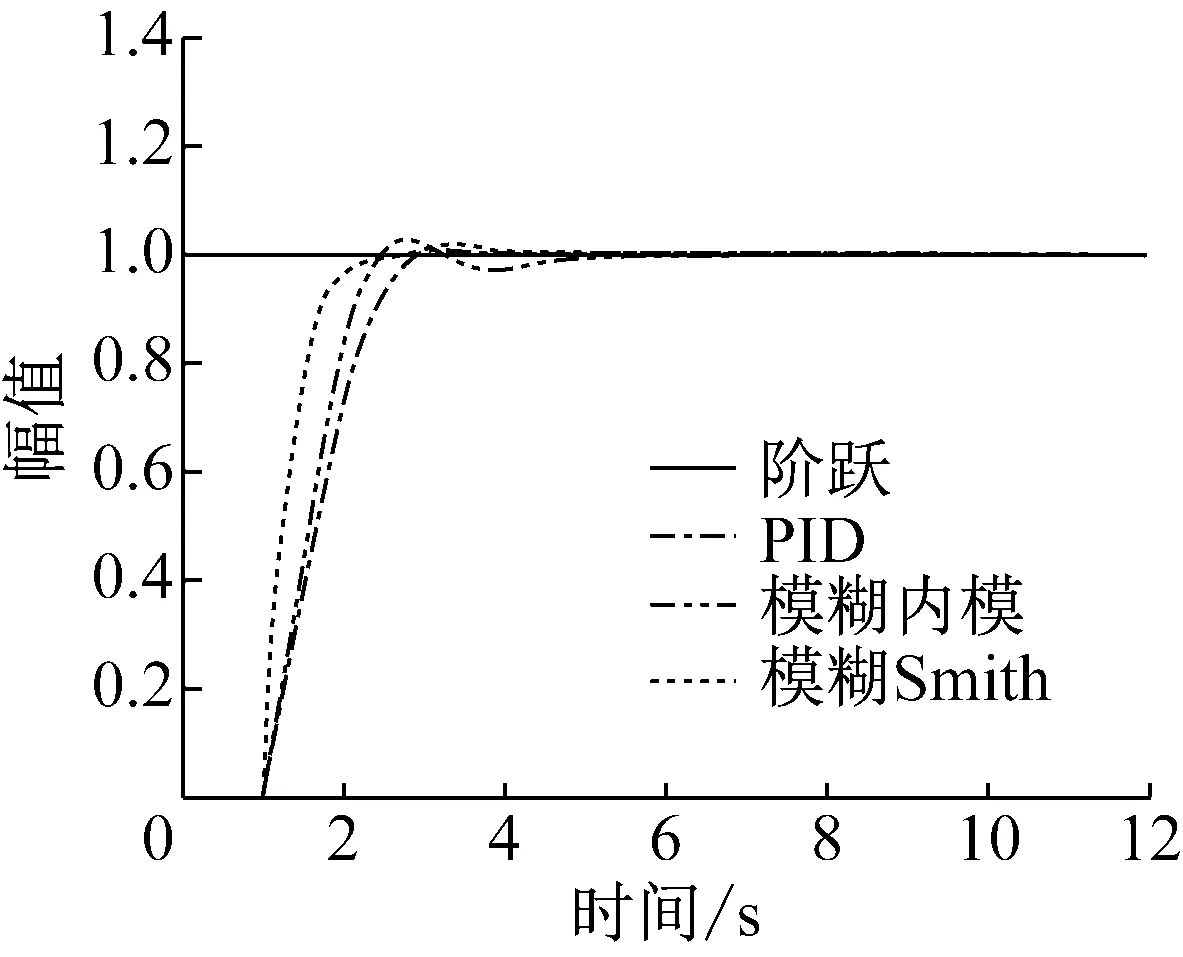
图13 3种控制方法阶跃响应比较图

在传统PID控制方法仿真时，对参数进行试凑调整，当ΔKp=1.6,ΔKi=0.56,ΔKd=0.45时，能兼顾快速性和稳态性能。其中，传统PID控制方法的响应时间为2.761，超调量为1.04%。

模糊Smith控制方法效果最好，响应时间最短，且无超调量，有很好的快速性和动静态性能。

模糊内模控制方法比传统的PID控制方法更快速，动态性能更优，但该方法也产生了一点超调量。就其快速性响应的性能而言，不如模糊Smith方法效果更好。

在工业过程中，智能阀门定位器将通过控制阀门的开度来控制液体流量的进出。系统响应的快速性提高能使阀门开度及时地进行调整，有利于对液体流量、快速达到要求，对工业生产的品质有一定的帮助。若阀门不能及时地进行响应，不仅会造成工业生产过程落后于工业要求的目标，甚至也有安全隐患。

与此同时，控制系统输出量的稳定性在生产过程中也占有很大的比重，输出量越接近设定量，控制过程越精确，越有利于生产过程的顺利进行；若系统输出不够稳定、超调较大，则不利于生产过程的精确控制，会导致生产效率不高，无形之中增加了成本，降低了经济效益；若输出大幅不稳定则可能产生安全问题。

所以，快速性和稳定性都要兼顾，需要综合考虑。由以上分析得，模糊Smith控制方法的动态响应和稳态性能均有很好的效果，能满足快速性和稳定性的要求，是一种有效的控制手段。

4 结 语

本文将模糊控制与Smith预估器设计结合，构成模糊Smith控制方法，将该方法与模糊内模以及传统PID控制方法进行对比。仿真结果显示，模糊Smith控制方法具有更好的动静态性能。对于工业过程，该方法能兼顾快速性和稳态性能，对智能阀门定位器进行及时和精确的控制提供了一种好的思路。

[1] 周欢喜. 气动智能阀门定位器设计与实现[D]. 南京: 南京理工大学, 2014.

[2] 金献军. 智能电气阀门定位器自整定算法研究[D]. 杭 州: 浙江大学, 2013.

[3] 赵明南,杨金堂,夏中愈,等. 智能阀门定位器控制方法的研究[J]. 机床与液压, 2015， 43(2):141-144.

[4] Zhang L, Fu W Y, Li Y H,etal. Design and simulation about a self-tuning fuzzy-PID controller[J]. Journal of CHONGQING University of Posts and Telecommunications(Natural Science Edition), 2009, 21(2): 192-195.

[5] Makara S T. PID fuzzy logic controller system for DC motor speed control[J]. Directory of Open Access Journals, 2004, 8(1): 25-27.

[6] 宋新甫,梁 波. 基于模糊自适应PID的风力发电系统变桨距控制[J]. 电力系统保护与控制, 2009， 37(16):50-58.

[7] Gaicia C E, Morari M. A unifying review and some new results[J]. Ind Eng Chem Proc Dev, 1982,21(2): 308-323.

[8] Edgar C R, Postlethwaite B E. MIMO fuzzy internal model control[J]. Automatica, 2000, 36(6): 867-877.

[9] 白建云,尹二新,李春晖. 基于PID的模糊内模控制在炉内脱硫系统控制中的应用[J]. 热力发电, 2015， 44(1):58-63.

[10] 刘启辉,文 云,张云龙. 基于一阶时滞系统的Smith预估器控制研究[J]. 工业控制与应用, 2014， 33(9):11-14.

[11] 曾庆良,顾 强,仉 毅,等. 基于Smith模糊PID控制的温室监控系统设计[J]. 计算机测量与控制, 2015， 23(6):1964-1966.

[12] 廖宣亮. 智能阀门定位器的设计[D]. 南昌: 南昌大学, 2012.

[13] 廖正军. 调节阀智能阀门定位器控制系统的研制[D].成都: 四川大学, 2003.

[14] 李 飞. 智能阀门定位器控制系统的研究[D]. 上 海: 上海应用技术学院, 2015.

[15] 诸 静. 模糊控制原理与应用[M]. 北京: 机械工业出版社,2005：303-306.

[16] Chen J, He Z F, Qi X. A New control method for MIMO first order time delay non-square systems[J]. Journal of Process Control, 2011, 21(4): 538-546.

Research on Intelligent Valve Positioner Based on Fuzzy-Smith Control Method

ZHANGHao1,WANGXin2,WANGZhenlei1,ZHIMaoxuan3,JIANGMingjing3

(1. Key Laboratory of Advanced Control and Optimization for Chemical Processes, East China University of Science and Technology, Shanghai 200237, China; 2. Center of Electrical &Electronic Technology, Shanghai Jiaotong University, Shanghai 200240, China; 3. China Petroleum & Chemical Corporation Zhenhai Refinery, Ningbo 315207, Zhejiang, China)

In view of the widespread phenomenon of time lag in the industrial control valve, a kind of intelligent valve positioner control method is proposed. The method is based on the fuzzy theory and Smith predictor. This paper analyzes of the structure and principle of smart valve positioner. Smith predictor is designed to compensate the delayed time and realize the advanced response. It overcomes the delay performance of the system. With the combination of fuzzy control and PID control, fuzzy rules are designed to adjust controller parameters. The combination of the two control schemes contributes to the fuzzy Smith method, which can improve the dynamic and static performances of the system. Fuzzy internal model controller overcomes the delay and improves the performance of the system. Simulating research of the fuzzy Smith controller, fuzzy internal model controller and PID controller shows that the fuzzy Smith control method is better than the fuzzy internal model control method and the traditional PID method because the first one can effectively improve the speed of the control valve, overcome the time delay and improve the performance of the system.

intelligent valve positioner; fuzzy Smith method; fuzzy internal model control; time delay

2016-09-28

国家自然科学基金面上项目(21376077)；国家自然科学基金优秀青年基金项目(61422303)；上海市自然科学基金项目(14ZR1410000，14ZR1421800)；流程工业综合自动化国家重点实验室开放课题基金资助项目(PAL-N201404)

张 浩(1993-)，男，山东潍坊人，硕士生，主要研究方向为控制系统性能。

Tel.:15800653081； E-mail:497629323@com

王振雷(1975-)，男，山东德州人，教授，博士生导师，主要研究方向为控制系统性能。

Tel.:021-64252640； E-mail: wangzhen_l@ecust.edu.cn

TP 273+.4

A

1006-7167(2017)05-0004-05