城市轨道交通断面客流不确定性分析的广义自回归条件异方差改进模型*
吴 婷 蒋阳升 丁 笑 郑世琦
(1.贵阳职业技术学院轨道交通分院,550081,贵阳; 2.西南交通大学交通运输与物流学院,610031,成都;3.西南交通大学综合运输四川省重点实验室,610031,成都; 4.西南交通大学交通运输智能化国家地方联合工程实验室,610031,成都∥第一作者,助教)
城市轨道交通断面客流不确定性分析的广义自回归条件异方差改进模型*
吴 婷1,2,3,4蒋阳升2,3,4丁 笑2,3,4郑世琦2,3,4
(1.贵阳职业技术学院轨道交通分院,550081,贵阳; 2.西南交通大学交通运输与物流学院,610031,成都;3.西南交通大学综合运输四川省重点实验室,610031,成都; 4.西南交通大学交通运输智能化国家地方联合工程实验室,610031,成都∥第一作者,助教)
对比分析指出,城市轨道交通线路断面客流量变化与道路交通断面客流量变化具有相似性,但城市轨道交通线路断面客流时间序列具备特有的尖峰厚尾特性,其变化的敏感程度依赖时空条件,常用于道路领域的广义自回归条件异方差(GARCH)模型无法直接用于城市轨道交通领域。基于此,引入广义误差分布(GED)虚变量,构建改进的GARCH模型,并基于成都地铁1号线下行断面客流时间序列数据,借助EViews和Matlab软件对改进前后的模型效果进行实证对比分析。结果表明,改进后的虚变量GARCH模型比原始的GARCH模型具有更好的适用性。
城市轨道交通; 断面客流; 不确定性; 虚变量; GARCH模型
First-author′s address Rail Transportation Branch,Guiyang Vocational and Technical College,550081,Guiyang,China
城市轨道交通线路断面客流的预测是轨道交通编制行车工作计划等运营决策的基础,但其预测精度常常难以保证。造成预测偏差的主要原因在于断面客流具有时变性,且不同断面对外部因素影响具有不同的敏感性,即客流变化的敏感程度具有强时空条件的依赖性[1]。因此,为提高线路断面客流的预测精度,不仅需要掌握城市轨道交通线路断面客流的平稳状态,即其一阶数字特征,而且更需要掌握断面客流的不确定性状态,即其二阶数字特征。它反映了断面客流时间序列中不可预见的组成成分对客流产生的影响,用来衡量统计时段内断面客流平均状态的波动性。对于一阶数字特征分析,文献[2-6]的工作已经比较完善;对于二阶数字特征的分析主要是定性研究[7]。经检索,国内外还没有专门针对城市轨道线路断面客流不确定性状态的量化建模分析。
城市轨道交通线路断面客流和道路交通流具有相似性,轨道交通各断面的客流运行情况类似于道路各个路段行驶的车流,因此探讨道路交通领域断面客流的不确定性分析的研究现状与趋势,以发现具有借鉴意义的分析方法,是一种有效的解决思路。
在道路交通领域,文献[1]使用一阶马尔科夫链阐述交通流不确定性变化规律,基于随机波动理论(SV)建立速度的不确定性模型。文献[8]将自回归滑动平均(ARMA)模型和广义自回归条件异方差(GARCH)模型结合,预测道路车辆行程时间及其不确定性,发现此模型对于严重拥挤路段,预测性能较优。文献[9]发现运用ARIMA(自回归积分滑动平均)模型与ARCH(自回归条件异方差)模型组合预测交通流不确定性性能,要优于标准的GARCH模型,其中,ARIMA模型预测高速公路断面交通流的平均状态,ARCH模型预测交通流的方差。文献[10]通过使用卡尔曼滤波方法实时处理GARCH模型,得到预测交通流量不确定性的置信区间,用同样方法实时处理SARIMA(季节性差分自回归移动平均)模型得到交通流量和速度的平均预测值。此外,文献[11]通过运用似不相关回归(SURE)模型,分别对出行者行程时间和出行者行程时间分布的标准差进行预测后,指出需对不确定性性能作进一步研究。
上述研究都是基于GARCH模型构建断面交通流状态不确定性模型,并在此基础上进行流量预测。这是因为GARCH模型能把序列方差随时间的变化情况呈现出来。但GARCH模型在城市轨道交通线路断面客流不确定性分析中不能直接应用,因为城市轨道交通断面客流与道路交通断面客流存在着差异,具体表现为:①城市轨道交通更关注早晚高峰和平峰时段的客流波动情况,以制定不同时段和线路区间的列车发车间隔等运营管理策略,城市轨道交通领域的模型需要能够刻画断面客流在时间(所有数据集合下的不同子集)和空间(不同断面)方面的敏感度;②城市轨道交通线路断面客流具有区别于道路断面客流的“尖峰厚尾”特征,文献[12]也指出采用广义误差分布(GED)比正态分布更符合实际情况,更能提高该模型的拟合效果和预测能力。
基于上述分析,本文拟建立基于GED分布的虚变量GARCH模型,以描述轨道交通线路断面客流的不确定性波动特征。
1 基于GED分布的GARCH模型
[12],GARCH模型形式如下:
yt=xtβ+εt
(1)
(2)
式(1)、(2)中:
yt——一个带有误差项的外生变量函数的均值方程;
xt——外生变量;
α、β——参数值;
εt——普通最小二乘法残差;
ht——εt的条件方差;
ω——常数项(均值);
p,q——模型的阶数。
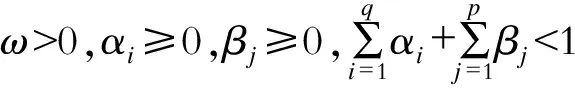
参考文献[13],利用广义误差分布对GARCH模型进行建模,其概率密度为:
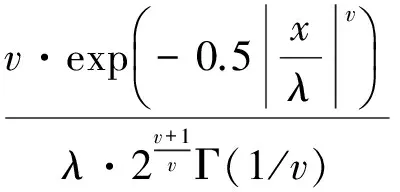
(3)
式中:
x——随机变量;
v——自由度,也是GED分布参数;
Γ(•)——Gama函数;
λ——尾部厚度参数,且
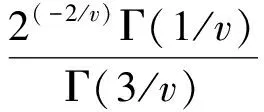
(4)
该峰度计算公式为:
(5)
式中:
E(X)——样本均值。
由式(5)可以看出,GED分布的形状(即峰度)由尾部厚度参数λ决定,其值的大小直接影响GED分布的尾部厚度。所以,广义误差分布是一种综合的、复杂的分布,能较好地描述时间序列具有非正态分布的“尖峰厚尾”特征[13]。
2 基于GED分布的虚变量GARCH模型与运用流程
2.1 虚变量的定义
本文将模型中能够被赋予具体数值的变量称为定量变量;不能赋予具体数值的变量称为定性变量。直接研究定性变量的影响具有一定的难度,因此本文通过设置虚变量将定性变量量化处理,使其和定量变量一样在模型中得以应用。
2.2 虚变量的设置
通常将虚变量取值为0和1,用D表示。D取值为1(0)时,表示该变量具有(不具有)某种属性。
2.3 虚变量GARCH模型
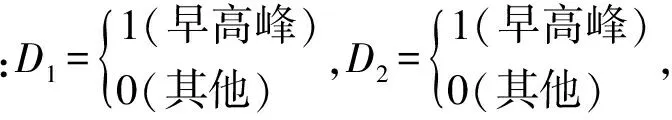
(6)
(7)
式中:
ai——q阶移动平均模型的系数;
bj——p阶自回归模型的系数;
ωi——反映序列波动的平均水平;
αi——回报系数,通过均值方程中误差项平方的滞后来反映前期得到的波动性信息;
βi——滞后系数,反映方差对外部冲击的记忆性。
2.4 基于GED分布的虚变量GARCH模型的运用流程
运用基于GED分布的虚变量GARCH模型进行城市轨道交通线路断面客流不确定性分析的步骤如下:
(1) 运用EViews软件计算各断面对数差分化的相对客流增长序列的基本统计量,验证该序列的“尖峰厚尾”特性,明确选取GED分布作为研究基础的合理性。
(2) 识别时间序列的平稳性和自相关性。如果序列的随机过程是非平稳的,则无法准确地反映该序列的过去和未来。自相关性检验主要是用来衡量不同序列随时间变化时的相互关系,通过观察序列的自相关函数和偏自相关函数进行判断。
(3) 模型类型和阶数的识别,即确认相应ARMA模型中阶数p和q的取值。
(4) 运用对数极大似然估计得到模型中所有参数的估计值,并采用对数似然准则(Log Likelihood准则)、赤池信息准则(AIC准则)和施瓦茨准则(SC准则)进行判断,当模型的对数似然值越大,同时AIC值和SC值越小时,说明模型估计越精确。具体技术流程如图1所示。
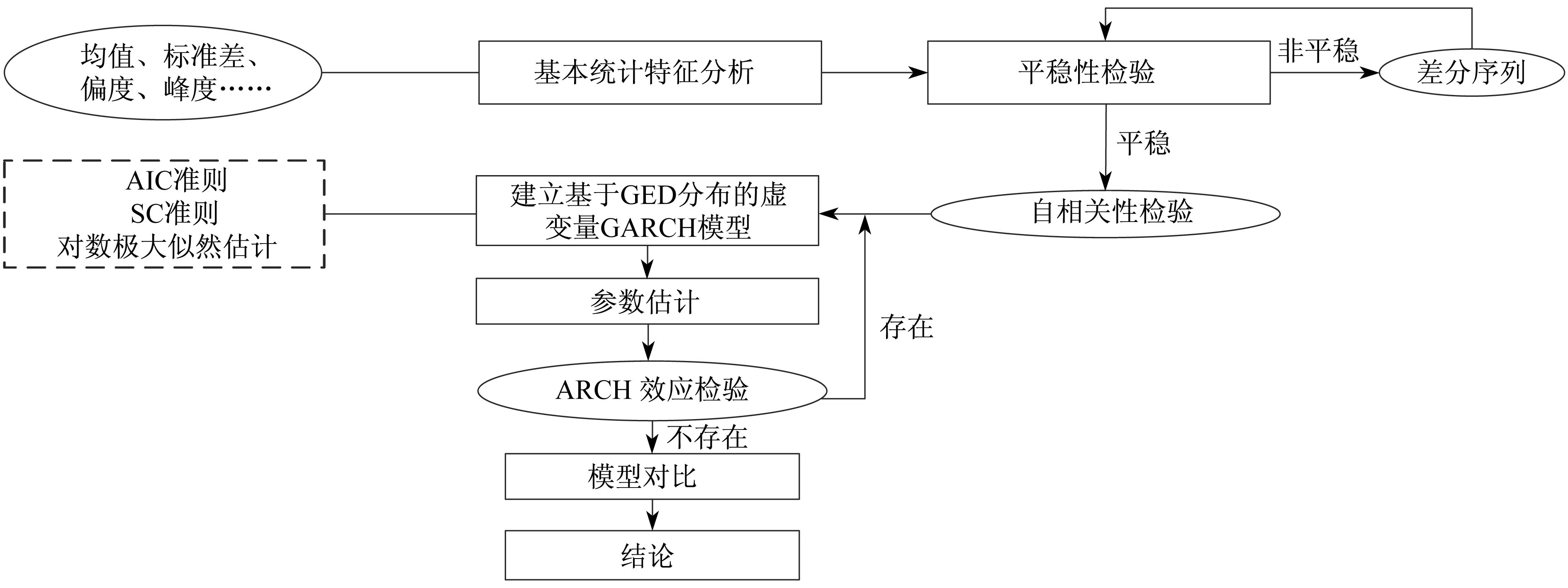
图1 技术流程图
3 实证分析
3.1 线路断面客流增长率基本特征分析
本文随机选取2013年3月整月平稳工作日(周二至周四)全日数据对成都市地铁1号线下行断面客流进行分析。从地铁开始运营6:30起,每1 h提取1次数据,直到当晚23:30停止运营时止。为了对早晚高峰时段进行分析,选取7:00—9:00为早高峰时段,17:00—19:00为晚高峰时段,其余为平峰。本文所指的断面客流为成都市地铁1号线16个站间的15个断面客流。为便于分析说明,1号线第一个断面升仙湖—火车北站简写为S1,第二个断面简写为S2,以此类推。
因为GARCH模型只能运用于平稳数据,而客流具有明显的高低谷之分,所以本文使用对数差分化的相对客流增长作为研究对象[1]。采取对数差分法的对数变换不仅能将增长曲线转化为线性趋势,而且进一步消除了序列的非平稳性。令Ri,t表示第i断面第t时间段的客流量,则第i断面第t时间段的客流对数增长率Yi,t为Yi,t=lnRi,t-lnRi,t-1。
运用软件计算断面客流增长率的基本统计量,结果见表1。表中Jarque-Bera表示一种正态性检验,Prob表示伴随概率。
由表1可知:从偏度看,所有客流的偏度系数均不为零,与正态分布相比具有明显的厚尾性;峰度方面,客流的峰度最小值为9.053 7(S15),大于3,相较于正态分布均具有偏尖峰性,说明所有断面客流较正态分布偏离程度更大,出现大起大落的情况比较严重。此外,Jarque-Bera统计量的伴随概率均为0,在95%的置信水平下,拒绝该时间序列为正态分布的假设。
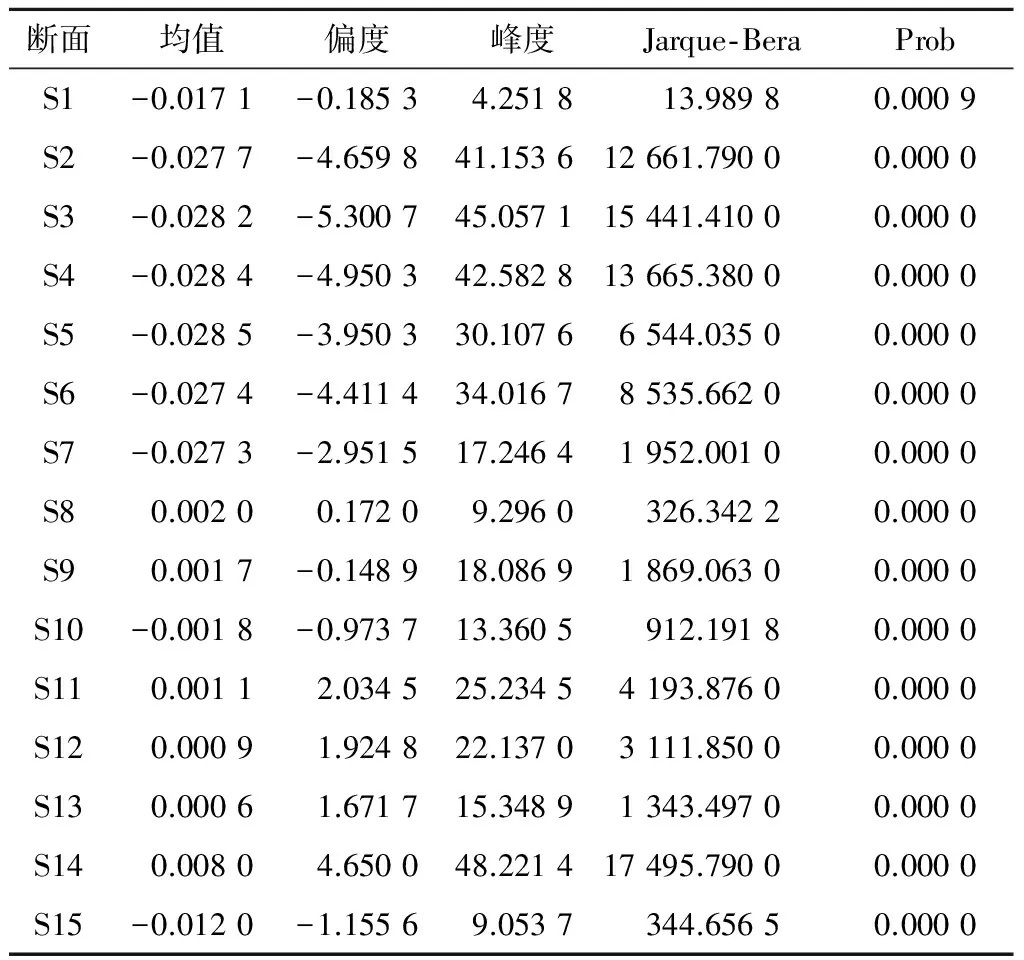
表1 断面客流增长率基本统计量
3.2 断面客流增长率序列的基础性检验
3.2.1 平稳性检验
单位根(ADF)检验结果如图2和图3所示。表中纵坐标表示在不同显著水平下的临界值,横坐标为各断面的检验值。
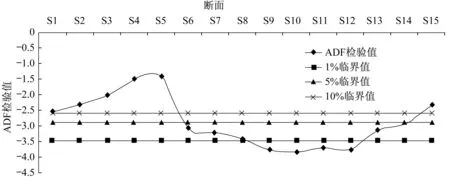
图2 各站断面客流原序列ADF检验
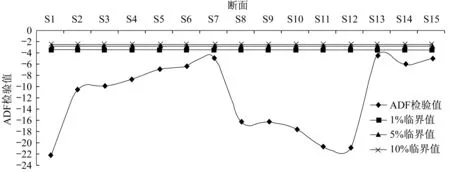
图3 各站断面客流差分序列ADF检验
从图2和图3可以看出:各站断面客流差分序列的ADF检验统计量均小于对应1%、5%、10%的临界值,说明其为平稳序列。为便于后续分析,将所有断面客流均转化为其对数差分序列来进行研究。
3.2.2 自相关检验
表2为各断面客流增长率在不同滞后阶数的自相关性检验结果表。由表2可知,15个断面客流的增长率序列在自由度为10、15、20时的Q统计量均大于相应的临界值18.307、24.996、31.410。说明在95%显著水平下,拒绝该客流序列没有自相关性的原假设,存在显著的序列自相关性。
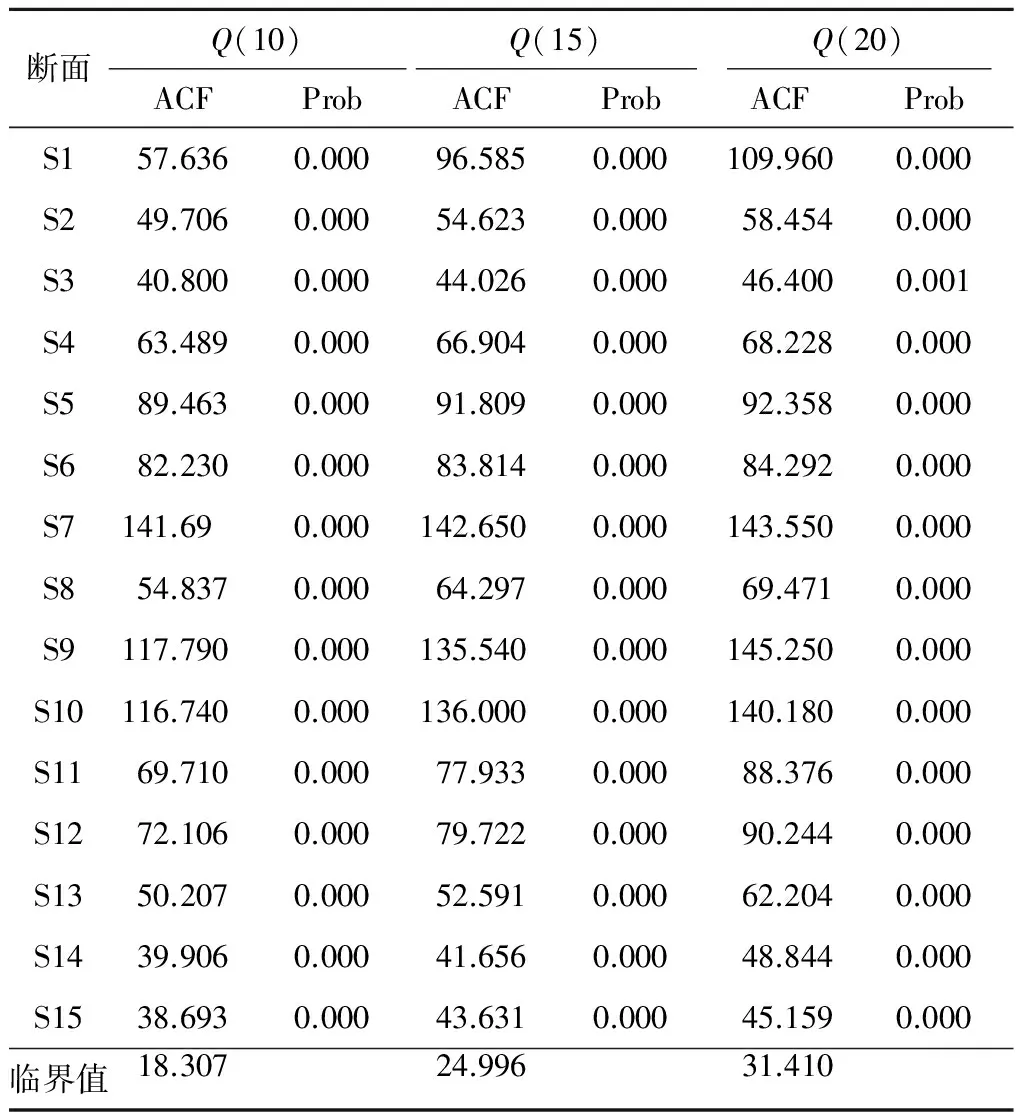
表2 断面客流增长率自相关性检验结果
3.3 虚变量GARCH模型实证结果分析
通过自相关检验中观察各断面客流的自相关(ACF)可知,各断面满足低阶模型,并经反复试算和对比所得参数,最终确定均值模型如表3所列。

表3 各断面客流和换乘客流对数增长率均值模型

续表3
运用软件Matlab编程实现参数估计和模型有效性检验,结果如表4、5、6所示。

表4 基于GED分布的虚变量GARCH(1,1)均值方程模型估计结果
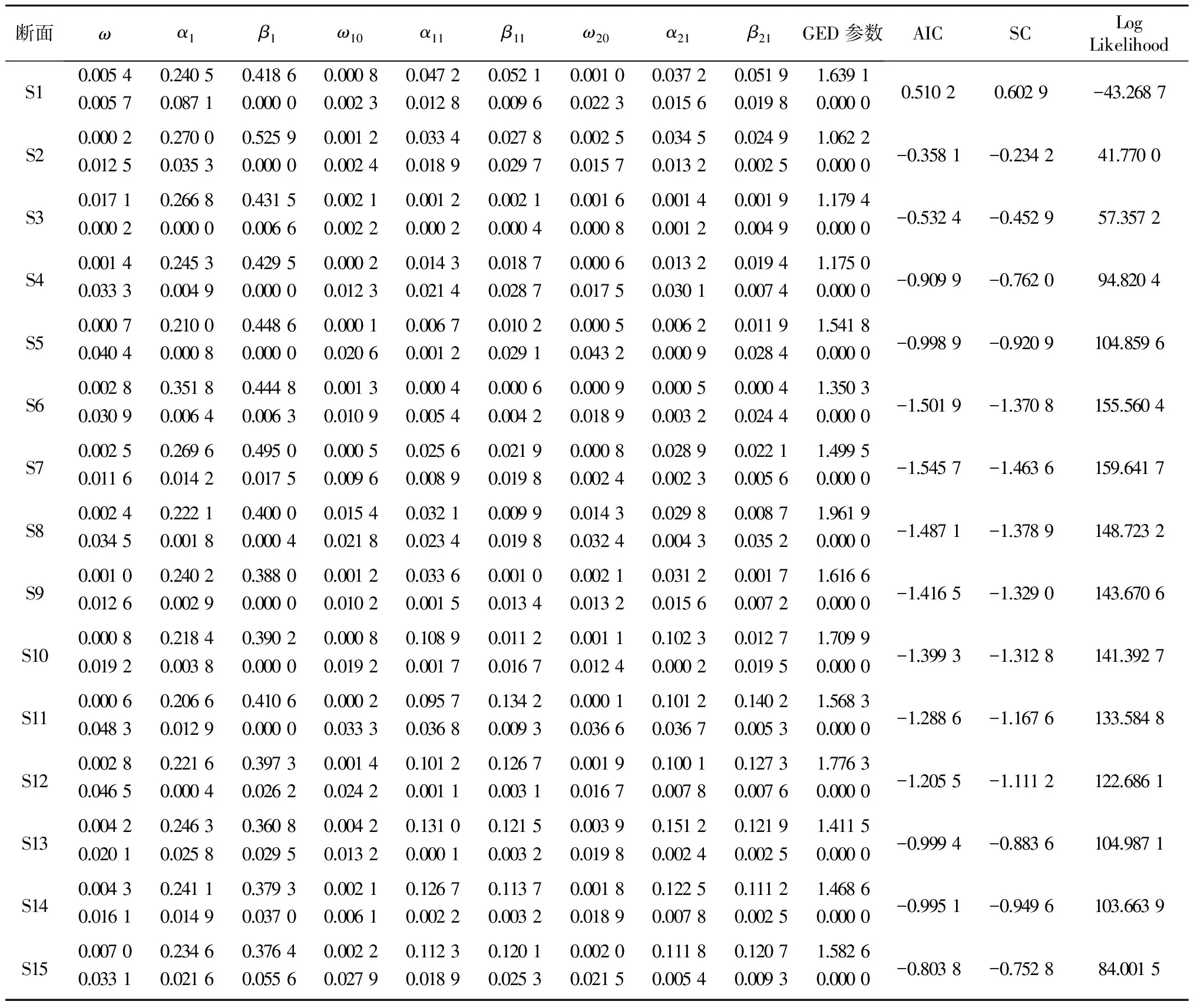
表5 基于GED分布的虚变量GARCH(1,1)方差方程模型估计结果
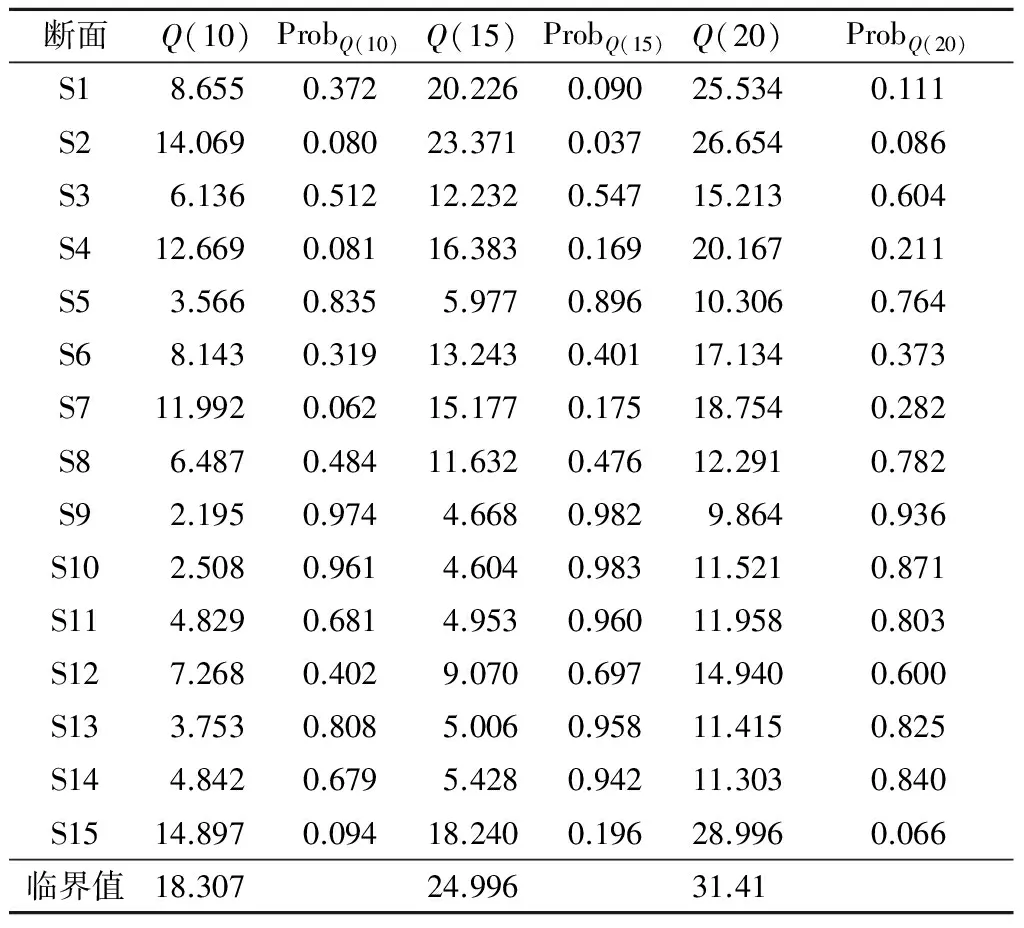
表6 虚变量GARCH(1,1)拟合结果Ljung-Box Q检验结果
由表6可知,所有断面在不同阶数的统计值均小于对应的临界值,且相应伴随概率均大于0.05,表明经拟合后的残差序列不具有相关性,另外方差方程中ωi、αi和βi值大于0,αi+βi<1,满足模型的平稳性要求,说明该模型正确。
为了说明该模型的优越性,本文将原始GARCH模型与虚变量GARCH模型进行对比,鉴于论文篇幅的限制,在此只列出模型评价参数AIC、SC和对数似然值,而原始GARCH模型的拟合结果可参考文献[14],结果见表7。
一般对数似然值越大,模型越精确,而AIC值和SC值则越小越好。从表7可知:所有断面客流基本是虚变量GARCH模型Log Likelihood值最大,AIC值和SC值最小(仅断面4的原始GARCH模型的AIC值和SC较小)。虽然在断面4中,其指标不是最优,但是其值大小和其他模型相差不大,而该断面的对数似然值却远大于另两个模型。所以,可以认定虚变量GARCH模型具有更好的适用性。
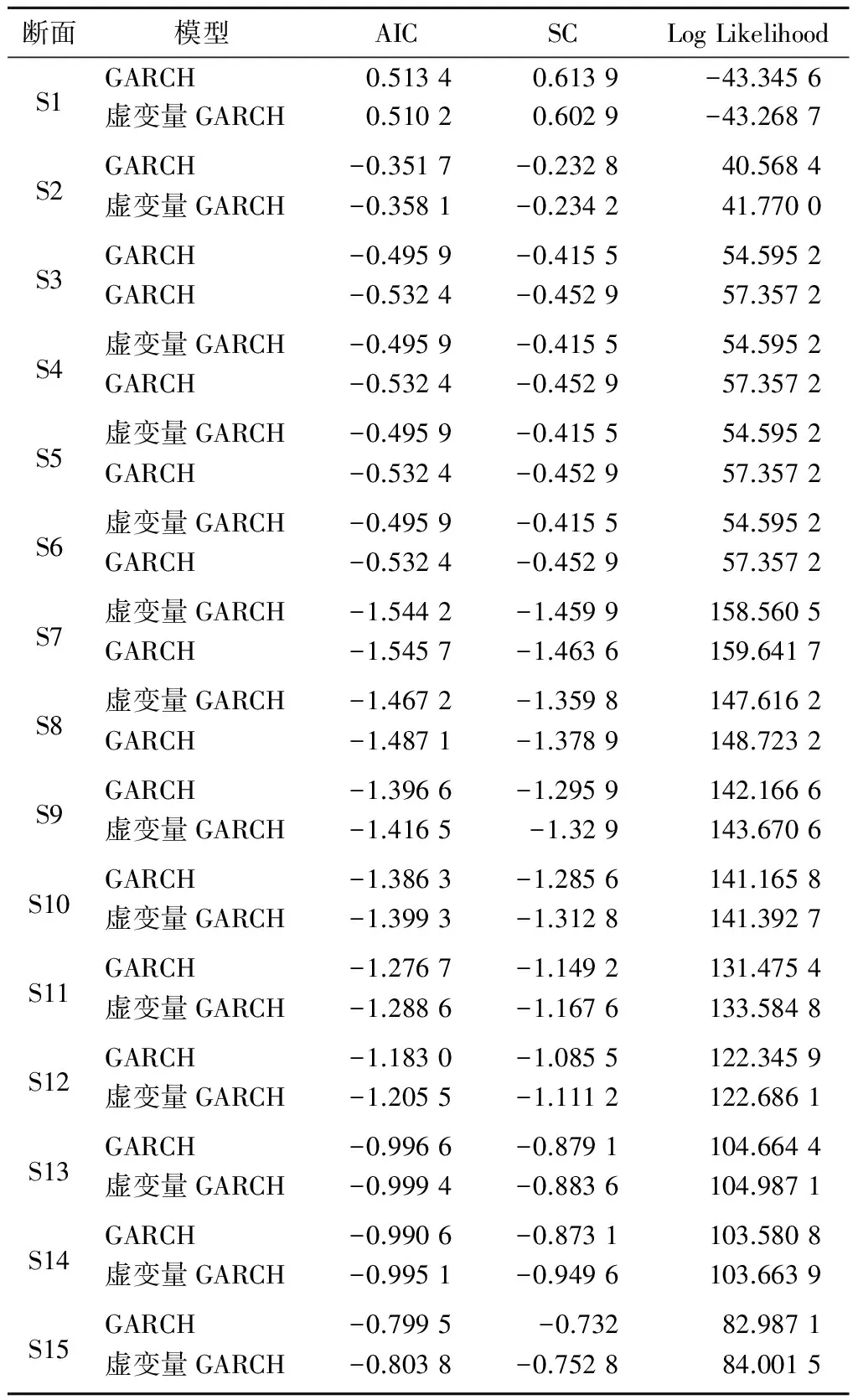
表7 GARCH模型和虚变量GARCH模型指标对比
4 结语
本文建立了基于GED分布的虚变量GARCH模型用于描述城市轨道交通线路早晚高峰和平峰时段不同断面的客流不确定性波动。基于成都地铁1号线下行断面客流数据的实证分析表明:改进后的模型能够更加适应描述城市轨道交通线路断面客流的尖峰厚尾特性和依赖时空条件的客流波动敏感性。本文研究为今后继续讨论不同因素对不同断面的影响程度奠定了基础。
参考文献
[1] TSEKERIS T,STATHOPOULOS A.Short-term prediction of urban traffic variability:Stochastic volatility modeling approach [J].Journal of Transportation Engineering,2010(7):606-613.
[2] 罗佳.城市轨道交通换乘站点客流敏感性分析[D].成都:西南交通大学,2014.
[3] 孙松伟.城市轨道交通客流预测模型及方法研究[D].成都:西南交通大学,2008.
[4] 杨冉.城市轨道交通客流预测及运营调度方法研究[D].北京:北京交通大学,2010.
[5] 袁坤.城际轨道交通客流预测方法研究[D].西安:长安大学,2009.
[6] 吴倩.城市轨道交通客流预测模型研究[D].成都:西南交通大学,2007.
[7] 郭平.城市轨道交通客流特征及预测相关问题[J].城市轨道交通研究,2010(1):58-62.
[8] SOHN K,KIM D.Statistical model for forecasting link travel time variability [J].Journal of Transportation Engineering,2009,135(7):440-453.
[9] TSEKERIS T,STATHOPOULOS A.Real-time traffic recasting in urban arterial networks [J].Transportation Research Record:Journal of the Transportation Research Board,2006(1964):146-156.
[10] GUO J,WILLIAM B M.Real-time short-term traffic speed level forecasting and uncertainty quantification using layered kalman filters[J].Transportation Research Record,2010(2175):28-37.
[11] MARTCHOUK M,MANNERING F,BULLOCK D.Analysis of freeway travel time variability using Bluetooth detection [J].Journal of Transportation Engineering,2010,137(10):697-704.
[12] 高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2009.
[13] 丁祖琴.基于GED分布GARCH模型的Bayes统计分析[D].上海:华东师范大学,2008.
[14] 吴婷.城市轨道交通断面客流不确定性研究[D].成都:西南交通大学,2015.
欢迎订阅《城市轨道交通研究》 服务热线 021—51030704
Improved GARCH Model in Urban Rail Transit Based on Uncertainty Analysis of Section Passenger Flow
WU Ting, JIANG Yangsheng, DING Xiao, ZHENG Shiqi
The variation of section passenger flow in urban rail transit is similar to that in road traffic through a comparative analysis. But the time series data of the former has peculiar characteristics of high kurtosis and fat tail, its sensitivity of variation depends on space-time condition.therefore,the GARCH model which is usually used in road traffic cannot be implemented directly in urban rail transit.For this reason,dummy variables are introduced to construct an improved GARCH model in this paper.Furthermore,based on the time series data of the downstream section passenger flow on Chengdu metro Line 1,the effects of models before and after improvement are comparative analyzed by using EViews and Matlab.The results show that the improved GARCH model with dummy variables has better applicability than that of the original GARCH model.
urban rail transit; section passenger flow; uncertainty; dummy variable; GARCH (generalized autoregressive conditional heteroskedasticity) model
*国家自然科学基金项目(51108391,71402149)
U 293.13
10.16037/j.1007-869x.2017.05.007
2016-06-24)