地震作用下某水利枢纽左岸坝前堆积体稳定性预测分析

彭仕麒，张志龙,2，费文平，莫济兴，徐 珍

(1.四川大学 水利水电学院，成都 610065；2.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059)

地震作用下某水利枢纽左岸坝前堆积体稳定性预测分析

彭仕麒1，张志龙1,2，费文平1，莫济兴1，徐 珍1

(1.四川大学 水利水电学院，成都 610065；2.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059)

某水利枢纽工程左岸坝前堆积体经历了5·12汶川大地震及4·20雅安地震，其内部的物理力学参数发生了恶化，稳定性有所降低。尽管现在该堆积体整体是稳定的，一旦再次经历类似的地震，其整体稳定状况会更加恶化，将对下游水利枢纽工程的安全稳定运行产生重大影响。运用FLAC3D数值模拟方法和Newmark法计算堆积体边坡在地震作用下的永久位移是很有必要的。计算结果表明：地震作用下堆积体发生位移部位主要位于压重体上方的小部分范围，产生的最大位移为0.56 m，同时根据位移和塑性区情况判断了堆积体的稳定性。最终预测出在类似的地震作用下，堆积体只会发生局部的浅表层蠕滑，整体仍是稳定的，研究成果为保证下游水利枢纽的安全稳定运行提供依据。

堆积体稳定性预测；地震作用；FLAC3D数值计算；Newmark法；蠕滑

1 研究背景

1.1 堆积体概述

某水利枢纽位于四川成都西北岷江上游，是一座以灌溉和供水为主，兼有防洪、发电、环境保护、旅游等综合效益的水电站。该水利枢纽工程左岸坝前堆积体位于库首沙金坝以上及引水系统进水口正前方，距右岸进水口最近水平距离250 m，距离大坝618 m，堆积体顺坡长1 600 m，沿江宽300～870 m，平面分布面积约1 km2，其体积达到了3 500～4 500万m3。左岸坝前堆积体方量巨大，一旦发生失稳，堆积体发生滑移，进入水利枢纽库区，产生高速涌浪，将直接淹没大坝，破坏该水利枢纽工程，并对下游居民的生命财产安全造成巨大的威胁。

在地质构造和岩性的影响下，岷江沙金坝河段形成一个180°的河曲，使得右岸形成三面环河的条形山脊，堆积体则位于岷江河谷左岸、库首沙金坝以上、左岸坝前位置。堆积体前缘较窄，向山内逐渐变宽，地貌上为圈椅状地形，由数个平台构成。堆积体整体上呈“陡—缓—陡—缓”的台阶状形态，坡体(尤其是中后部坡体)相对较厚，基覆界面呈上陡下缓的犁式，灯盏坪后缘基覆界面可达50°左右，灯盏坪下部顺坡向基岩顶面平均坡度仅5.75°，葫豆坪后缘基覆界面顺坡向平均坡度为15°左右，前部坡度则较缓。根据勘探资料，堆积体主要由块碎石土、黏土夹块碎石和块碎石夹黏土组成。主要物质成分为灰岩、白云岩、白云质灰岩等组成。堆积体综合地质平面图和堆积体纵Ⅰ—Ⅰ地质剖面图如图1和图2所示。

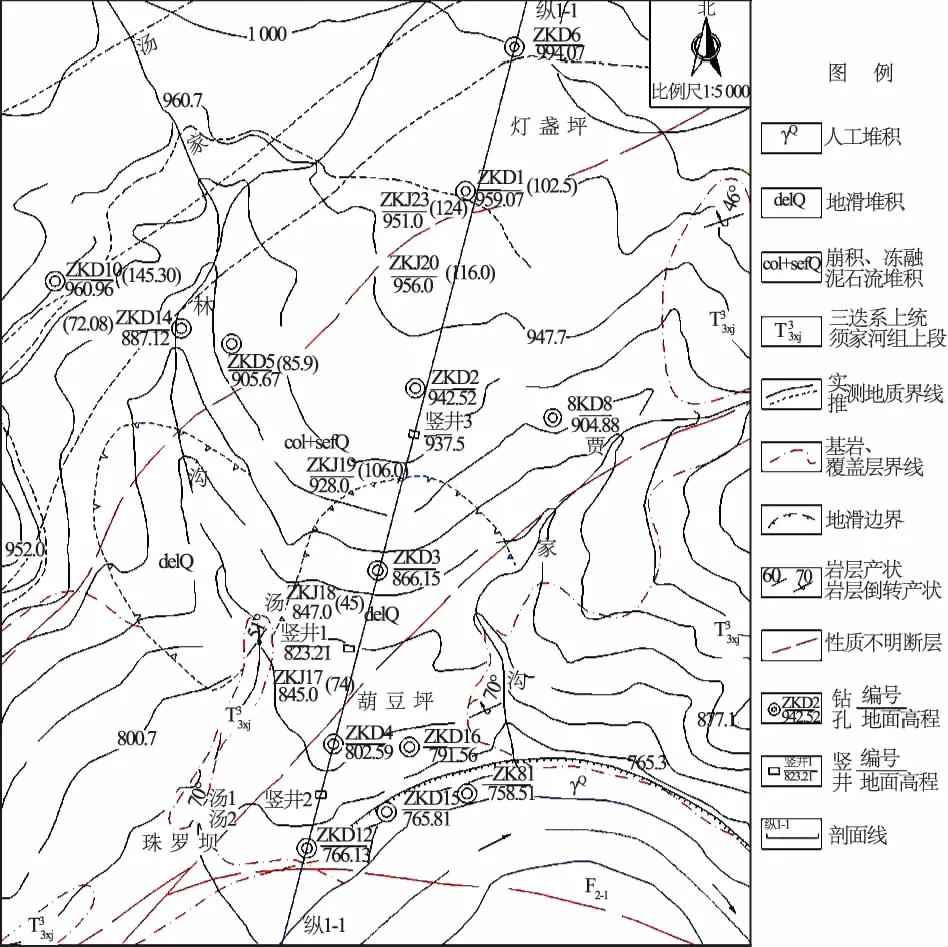
图1 堆积体综合地质平面图Fig.1 Comprehensive geological map of accumulation body

图2 堆积体纵Ⅰ—Ⅰ地质剖面图Fig.2 Geological profile of section Ⅰ—Ⅰ of accumulation body

1.2 堆积体稳定情况

堆积体使用堆碴压脚来提高初始的稳定性，这起到了较为良好的效果。在未发生地震时，整体是稳定的。“5·12”地震后，李巧[1]通过对堆积体变形监测数据并结合数值计算数据分析得出在“5·12”汶川大地震作用下堆积体产生了一定的变形，但整体仍是稳定的；汪家林等[2]、彭仕雄等[3]也通过各种方法论证了堆积体在汶川地震下整体是稳定的，只是局部失稳。这说明堆积体在汶川大地震的作用下，总体是处于稳定状态的，对下游水利枢纽影响较小。

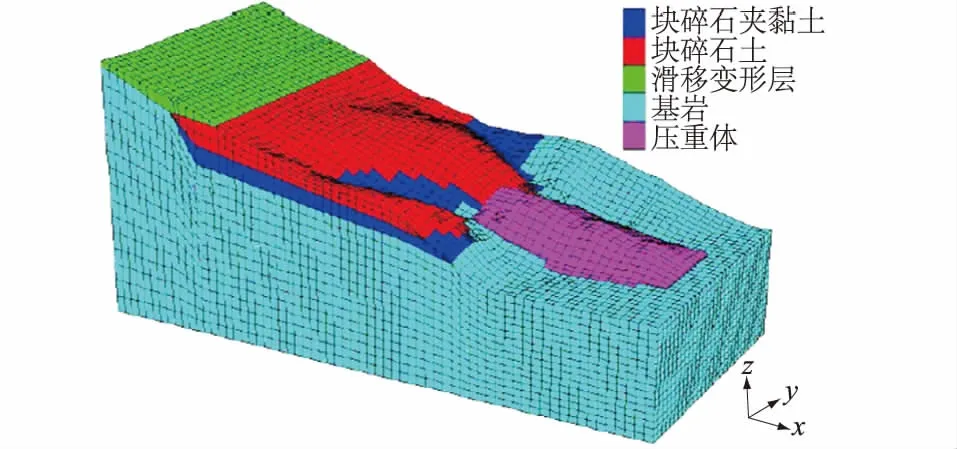
图3 堆积体三维计算模型Fig.3 Three-dimensional calculation model ofaccumulation body

2 堆积体数值模型计算

2.1 计算模型及参数的确定

结合堆积体地质资料分析，堆积体边坡的稳定性很大程度上受影响于自重应力，构造应力的影响很小，因此在其稳定性分析评价时基本荷载为自重。计算模型的建立以堆积体纵Ⅰ—Ⅰ剖面x轴，指向坡外为正；y轴为垂直于纵Ⅰ—Ⅰ剖面方向，指向下游侧为正，z轴为铅直方向，向上为正。根据堆积体的地质结构和岩土体的力学特性，可将计算模型材料分为块碎石夹黏土、块碎石土、滑移变形层、基岩和压重体材料，计算模型如图3所示。

在进行堆积体模型计算时，本构模型使用Mohr-Cloumb模型，岩土体错动变形的计算力学参数包括了体积模量K、剪切模量G、内摩擦角φ、内聚力c、抗拉强度T及重度γ等参数。由于现在一般使用弹性模型E和泊松比μ表述岩土体的物理力学参数，需将其进行转换为K和G，它们之间的关系为[4]:

(1)

(2)

左岸坝前堆积体边坡各岩土体的物理力学参数根据地质勘察报告，参考泄滩、呷爬滑坡等滑坡[5-8]，具体各岩土体及支护材料的物理力学参数取值如表1所示。

表1 堆积体上各岩土体物理力学参数

2.2 边界条件及动力荷载的施加

FLAC3D在计算动力问题时，边界条件分为远置人工边界和黏滞边界，计算时模型的边界条件的选取很重要。刘春玲等[9]认为:远置人工边界会对入射波进行完全的反射，这样的边界条件会对计算结果产生一定的影响，要消除这种影响，需要将模型边界取得足够远，但是这在岩土工程的计算中还未进行此项研究，所以采用远置人工边界的方法几乎是不可取的。同时在FLAC3D中黏滞边界一般分为2种，有静止边界和自由场边界。本文在静力计算时，在模型的底部施加固定约束边界以及模型四周为单向约束边界，坡体表面为自由边界，并仅考虑自重应力产生的初始应力场；在动力计算中边界条件的设置采用自由场边界。同时本文在动力计算中力学阻尼选取采用了瑞利阻尼，取其值为5%。

在地震动力计算时采用加速度时程分析法，输入的地震波是从随机合成的60条波中任意选取1条作为计算输入地震波(图4)，并参考孔宪京等[10]文中的地震加速度波，合成60条时程的平均峰值加速度(PGA)为2.62 m/s2。模拟地震波持续时间45 s，地震动力时程计算60 s(即地震波结束后继续计算15 s以反映地震荷载作用可持续发生的不可恢复变形)。

图4 输入地震波加速度时程图(PGA=2.62 m/s2)Fig.4 Time-history curve of input wave acceleration(PGA=2.62 m/s2)

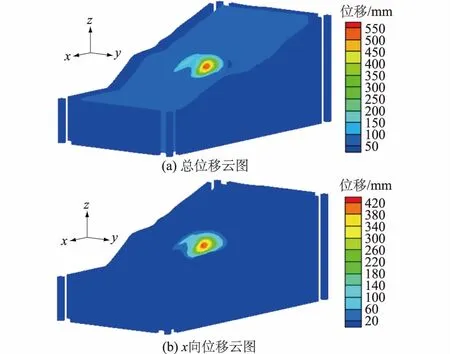
图5 堆积体总位移及x向位移云图Fig.5 Total displacements of accumulation bodyand displacements in x direction

在动力计算中的地震波是从计算模型底部边界输入，包括x向和z向2个方向的地震波，依据水工建筑物抗震设计规范的建议，将z向的地震波幅值取为x向峰值的2/3。

2.3 堆积体变形数值成果分析

在地震加速度为0.26 g的地震作用下，堆积体的合位移、x向位移变形特征如图5所示。

从图5中可看出:堆积体在地震作用下总位移整体上是保持一致的，但局部地方位移较大，最大位移处发生于堆积体压重体的上方，变形总位移的最大值为0.56 m。同时，从堆积体的x向位移和z向位移变形特征也可以看出:堆积体边坡x向移动的最大位移为0.43 m，且位移主要发生于压重体的上部区域，说明了该堆积体坡脚进行压重体压脚处理，使得地震作用下堆积体在灯盏坪前缘受阻，变形位移不能较好地往下传递，这对堆积体的整体稳定是有利的。

从堆积体塑性特征(图6)可以看出:堆积体后缘表层、潜在底滑面处于剪切状态，而较深层的基岩的状态并未发生变化，说明只是表层土体可能发生了滑动，堆积体整体还是稳定的。在地震作用下，堆积体前缘发生了表层错动变形,但是并没有贯通发生滑坡，说明堆积体在进行压重治理后,即使再次经历大地震，总体上还是稳定的。

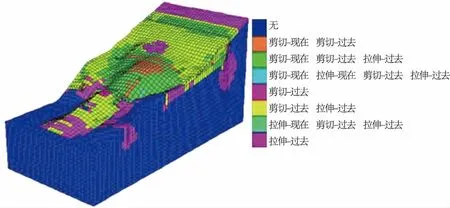
图6 堆积体塑性特征Fig.6 Plastic characteristic of accumulation body

3 堆积体永久位移特征Newmark法分析

1965年Newmark在第五届朗肯讲座上[11]提出用边坡的永久位移来判断在地震作用下边坡是否发生失稳，并且在随后的研究中验证了Newmark法的可靠性。例如Wilson等[12]研究得出在1979年Coyote Lake地震中，Newmark法计算得出的滑坡位移量与实际的滑坡位移量十分接近；同时A.S. Al-Homoud等[13]应用该法计算预测了边坡在地震荷载作用下的永久位移，与实测地震位移对比得出，认为使用Newmark法计算得出的边坡位移比实测位移要小，但是结果比较接近。所以本文主要运用Newmark法对堆积体的稳定性进行评价，并与之前FLAC3D所计算的结果进行对比，判断预测结果的可靠性及其稳定性。

3.1 Newmark计算方法简介

使用Newmark法计算时首先要明确它的基本假设条件[14]，即：①把滑动坡体看作刚性块体，其内部不产生变形；②只有地震加速度超过临界加速度时才产生滑动位移；③土体受到的动静剪切力均一致；④运行过程中忽视动态孔压的影响；⑤整个计算过程中，临界加速度被视为常量；⑥只有下坡向的位移，上坡向的位移完全受到抑制。

Newmark法认为滑体滑动时都存在一个临界加速度ac，当地震加速度超过临界加速度ac时，滑动体将克服摩擦阻力开始滑动。其临界加速度的计算公式为

(3)

式中：Fs为边坡静力安全系数;g为重力加速度;θ为滑体滑动方向与水平线的夹角。同时，根据地震加速度和临界加速度，计算边坡滑体的累积永久位移，通过计算得出的累计位移量来判断边坡或者滑体是否稳定，其累计位移由对加速度进行双重时间积分得到，即

(4)

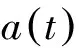
3.2Newmark法计算累计位移

在堆积体最不利工况下，根据浸润线1(如图7)，用极限平衡法计算可得出堆积体边坡的静力安全系数为1.07，代入式(3)可得出临界加速度ac为0.19m/s2。

图7 堆积体最不利工况下计算简图Fig.7 Calculation diagram of accumulation body underthe most unfavorable conditions

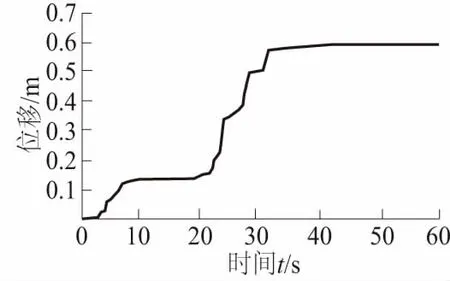
图8 位移-时间过程曲线Fig.8 Curve of displacementvs. time

通过式(4)计算累计位移(如图8)，其中地震波加速度仍用之前所采用的。由于计算静力安全系数时为浅表层土产生滑动，即计算出来临界加速度及累计位移也为表层块碎石土的，即发生部位位于浸润线1的上面部分，位移量为0.59 m。

4 结 论

本文以数值模型计算为主线，并采用Newmark法对某左岸坝前堆积体在地震作用下的稳定性情况进行研究，对堆积体以后遭遇强震下的稳定性进行预测。主要计算结果对比以及结论分析如下：

(1) 通过对坝前堆积体进行三维建模，再用FLAC3D软件进行数值计算，得出的堆积体在地震作用下的最大位移为0.56 m，该最大位移位于压重体上部的小部分范围，从位移矢量图中可以看出为表层块碎石土滑动。同时，根据堆积体塑性特征图可以看出只是表层土体出现剪切状态，深层基岩并没有出现，所以说堆积体整体还是稳定的。

(2) Newmark法根据静态稳定安全系数计算得出临界加速度，然后进行二次积分得出的堆积体在地震作用下的永久位移为0.59 m。该位移为局部位移，发生部位位于最不利工况下的浸润线1的上部，为浅表层土滑动。

(3) 通过上述2种方法计算预测某水利枢纽左岸坝前堆积体在地震工况下的稳定性，可以得出用两种方法计算得出的位移基本是相吻合的，说明用FLAC3D和Newmark法计算出来的位移较为准确，产生较大位移均为局部位移，整体稳定性较好，对下游电站的影响较小。

另外，当前建立的数值模拟模型是基于传统的连续介质有限变形分析，与堆积体实际力学特征有一定的差异。建议今后有必要采用离散元或其他非连续变形分析方法，在运用动力时程分析法进行地震分析时，进一步开展堆积体动力方面的研究,并考虑暴雨、堆积体内地下水的变化及库水位的升降对堆积体稳定性的影响，使计算结果更接近实际。

[1] 李 巧.紫坪铺水利枢纽工程坝前堆积体的地震动态响应及稳定性复核研究[D].成都：成都理工大学,2012.[2] 汪家林, 徐湘涛, 汪贤良, 等. 汶川8.0级地震对紫坪铺左岸坝前堆积体稳定性影响的监测分析[J]. 岩石力学与工程学报, 2009,28(6): 1279-1287.

[3] 彭仕雄, 杨 建, 张世殊, 等. 紫坪铺水利枢纽工程震损地质调查分析研究[C]∥汶川大地震工程震害调查分析与研究.北京：科学出版社，2009.

[4] 彭文斌. FLAC3D实用教程[M]. 北京: 机械工业出版社, 2007.

[5] 朱继良, 黄润秋. 某水电站坝前堆积体稳定性的三维数值模拟分析[J]. 岩土力学, 2005,26(8): 1318-1322.

[6] 王 琛, 胡德金, 刘浩吾, 等. 三峡泄滩滑坡体滑动带土的蠕变试验研究[J]. 岩土力学, 2003，24(6): 1007-1010.

[7] 张雪东, 陈剑平, 黄润秋, 等. 用FLAC-3D分析呷爬滑坡的变形特征[J]. 岩土力学, 2005,26(1): 131-134.

[8] 丁秀美. 西南地区复杂环境下典型堆积(填)体斜坡变形及稳定性研究[D]. 成都：成都理工大学, 2005.

[9] 刘春玲, 祁生文, 童立强, 等. 利用FLAC3D分析某边坡地震稳定性[J]. 岩石力学与工程学报, 2004，23(16):2730-2733.

[10]孔宪京, 周 扬, 邹德高, 等. 汶川地震紫坪铺面板堆石坝地震波输入研究[J]. 岩土力学, 2012，33(7):2110-2116.

[11]NEWMARK N M. Effects of Earth quakes on Dams and Embankments[J]. Geotechnique, 1965,2(15)：139-160.

[12]WILSON R C, KEEFER D K. Dynamic Analysis of a Slope Failure from the 6 August 1979 Coyote Lake, California, Earthquake[J]. Bulletin of the Seismological Society of America, 1983,73(3): 863-877.

[13]AL-HOMOUD A S, TAHTAMONI W. Comparison Between Predictions Using Different Simplified Newmarks’ Block-on-plane Models and Field Values of Earthquake Induced Displacements[J]. Soil Dynamics and Earthquake Engineering, 2000,19(2): 73-90.

[14]刘圆圆, 王星华. 利用改进的Newmark方法探讨高陡岩质边坡稳定性[J]. 世界地震工程, 2013，29(4):147-152.

(编辑：赵卫兵)

Stability of Left Bank Accumulation Body in front of a Dam underEarthquake: Prediction and Analysis

PENG Shi-qi1，ZHANG Zhi-long1,2，FEI Wen-ping1，MO Ji-xing1，XU Zhen1

(1.School of Water Resources and Hydropower，Sichuan University，Chengdu 610065，China; 2.State Key Laboratory of Geohazard Prevention and Geoenvironment Protection， Chengdu University of Technology，Chengdu 610059，China)

Having experienced 5·12 Wenchuan earthquake and 4·20 Ya’an earthquake, the left bank accumulation body in front of a hydro-junction has degraded in its stability and physico-mechanical parameters. Although the accumulation body is stable in general at present, its overall stability will have a significant impact on the safe and stable operation of downstream hydro-junction when similar earthquake occurs again. In view of this, we calculated the permanent displacement of the accumulation body under earthquake action by using FLAC3Dand Newmark Method. We conclude that the displacement of the accumulation body is mainly located in the small part above the pressure body, and the maximum displacement is 0.56m. Furthermore, we estimated the stability of the accumulation body according to the displacement and plastic zone. The accumulation body will still be stable as a whole under similar earthquakes, with only local shallow surface creep. The result offers a basis for ensuring the safe and stable operation of the downstream hydro-junction.

prediction of accumulation body stability; earthquake action; FLAC3Dnumerical calculation; Newmark method; creep; mechanical parameters

2016-03-17；

2016-04-27

地质灾害防治与地质环境保护国家重点实验室开放基金项目(SKLGP2012K015)

彭仕麒(1992-)，男，江西吉安人，硕士研究生，主要从事地质工程、岩土工程等方面的研究，(电话)18328006088(电子信箱)1044823871@qq.com。

张志龙(1975-)，男，内蒙古商都人，讲师，博士，主要从事地质灾害防治、工程边坡稳定性分析等方面的研究工作，(电话)13558872211(电子信箱)zzlxww@scu.edu.cn。

10.11988/ckyyb.20160240

2017,34(6):114-118

P315；P642.2

A

1001-5485(2017)06-0114-05