让“教”与“学”不再“唱双簧”
李芸
[摘 要]“用字母表示数”这一课是学生首次正式接触代数领域的内容,标志着学生的思维由算术空间正式进入代数空间,其重要性不言而喻。通过“在不疑处设疑”“在存疑处释疑”“在释疑后释放”,对“用字母表示数”的教学设计进行改进与思考,实现教与学的有效互动。
[关键词]代数;字母;教学设计;教与学
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2017)17-0036-01
学习代数知识前,学生已充分掌握各种运算律,对常见数量关系等基础知识也非常熟悉。通过用字母代表数,用含有字母的代数式进行运算并借此表述各种等量关系,可为以后学生学习方程做好铺垫。由数字运算一下子过渡到字母运算,学生思维节奏往往会跟不上。因此,帮助学生正确理解与认识代数式的意义与先进性,是本单元教学的重点。
一、在不疑处存疑
师(出示课本例2):例题中的英文字母b代表什么?具体可以是什么数字?
生1:表示已走的行程,大小介于0~280之间。
师:那280~b这个式子又代表什么?
生2:代表剩下的行程。
师:如果再选用一个英文字母“c”代表剩下的行程,你能用含有b和c的式子表示它们之间的数量关系吗?
生3:c=280-b。
师:因此我们可以下结论,单独一个字母可以代表一个数,放入等式中可以表示数量关系。
由此可知,字母既可以代表数字,也可以代入等式表示数量关系。不过,此处存在两点疑问:
第一,“b”是个“未知数”,用“280-b”表示解题结果,实际上结果仍是未知的。这也正是算术空间与代数空间的不同之处,算术是为了确定结果的数值,代数往往只是揭示内部规律。
第二,教材中,例1到例2就由离散量忽然转向连续量,会引起学生质疑:既然用含有字母的代数式表示解题结果比数字更管用,那学数字计算还有什么用?看来,问题的症结不在于运算结果换了一个表达形式,而在于字母的不确定性带来的更为广阔的思考空间。
二、在存疑处释疑
出示:北京、天津两城的地铁站间的距离为280千米。一辆地铁从北京开往天津,已行驶一段距离,剩下的路程是( )千米。
师:总路程、已行驶的路程、未行驶路程这三者之间的关系你能用线段图表示出来吗?
生1:我把总路程一分为二,一段表示已行驶路程,一段表示未行驶路程。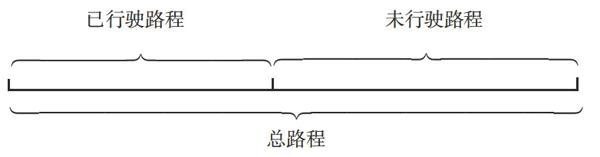
师:在这里,已行驶路程知道是多少千米吗?
生2:题目没有交代。但是,不论它是多少,我们都能利用“总路程-已行驶路程=未行驶路程”这个公式求出来。
生3:我用字母 b代表已行驶路程,未行驶路程程则用(280-b)表示。
教学改进后,教师没有刻意让学生用式子表示运算结果,而是引导他们先用语言文字表述数量关系并将三者之间的关系用线段图表示出来。学生的主观能动性被这一开放的活动情境有效激发出来了,他们不仅会根据数量关系进行具体的数值运算,而且会借助简明扼要的文字式来直观反映数量关系,部分学生还能自主地采用字母来表示未知变量,并顺理成章地想到用代数式“280-b”表示剩下的路程。
三、在释疑后释放
回顾“用字母表示数”一课的改进历程,无论多么基础的知识内容,我们都要不断探本求源,研磨出贴合学生的课堂互动环节,力求让“教”与“学”自然发生,使离学生感知经验较远的知识能在学生头脑中生根。
数学学习的主体永远是学生,教师的职责只是教学的设计者、主持者、组织者和引导者。教师要想方设法把学生学习的积极性和主动性调动起来。数学活动的主要形式是全员(包括师生、生生)互动,而保证互动有效性的正是能促进思维发展的一系列問题。现实性与趣味性是数学教学中选择问题情境的重要标准。教师不但要学会做教学设计的加法,更要学会做教学设计的减法,只有把形式主义赶出去,才能释放出更多创新的活力与空间。
(责编 罗 艳)

