思维方法运用的典范
——卡文迪许扭秤实验赏析①
陈连余
(江苏省南京市金陵中学,江苏 南京 210005)
·名师论坛·
思维方法运用的典范
——卡文迪许扭秤实验赏析①
陈连余
(江苏省南京市金陵中学,江苏 南京 210005)
科学思维是物理核心素养的有机组成,思维方法教育则是“授人以渔”教学理念的具体表现.卡文迪许扭秤实验是物理学的“十大美丽实验”之一,其中包含很多精彩设计,本文拟就该实验所运用到的思维方法作一番剖析.
卡文迪许扭秤实验;万有引力;思维方法
2002年美国《物理学世界》公布了物理学的“十大美丽实验”的评选结果,卡文迪许扭秤实验榜上有名.那么,卡文迪许扭秤实验中究竟蕴藏着哪些“美丽”?笔者将从思维方法的角度作一些剖析.
1 相关背景
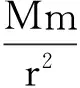
1775至1778年英国剑桥大学的机械师米切尔提出:用扭秤有可能在实验室里直接测量物体之间的吸引力.受到米切尔实验思想的启发,英国物理学家卡文迪许设计出了倒T形支架实验装置,如图1所示,其中木棒长度为6英尺(1英尺等于30.48厘米),木棒两端固定小铅球m1、m2,其直径均为2英寸(1英寸等于2.54厘米),在m1、m2附近各固定一个直径为12英寸、质量为350磅(1磅约等于0.45千克)的大铅球M1、M2.在木棒中点系上长为39英寸细金属丝后悬吊起来.在M1对m1、M2对m2的引力作用下,倒T形支架将会产生微小的转动,并扭转金属线.测出悬丝的扭转角度,结合悬丝的扭力常数,就可以计算出倒T形支架所受扭力的大小.

图1
1798年卡文迪许发表了论文“测定地球密度的实验”,在论文中他总结了17次实验的结果,计算出了地球的质量为5.89×1024kg.结合地球半径的数据,得出地球的平均密度是水密度的5.481倍.

2 实验中的思维方法赏析
在牛顿时代,包括牛顿在内的许多科学家在万有引力的测量方面做过努力,都没有能够取得成功.卡文迪许汲取了前人的经验,设计出了扭秤实验装置,排除了诸多可能影响实验准确性的因素,最终取得成功.在实验中,卡文迪许运用了多种思维方法,我们逐一进行赏析.
2.1 放大法
众多科学家在测量万有引力的数值时为什么会失败?原因在于引力十分微弱,数值太小.要想对微小的引力进行显性观察、计量,只有借助于放大手段.卡文迪许受到米切尔实验思想的启发,设计出了如图2所示的实验装置.在装置中,几次对小量进行了放大,这样既便于观察实验现象,又利于对实验结果进行测量.

图2
(1) 放大微弱引力F的转动效果
倒T型架在两端各自受到微弱引力F,为了显现F对倒T型架的转动效果,卡文迪许放大了引力F的力臂——倒T型架的长度L,据史料记载该长度达到1.8米.这样,虽然引力F十分微弱,但是由于其相应的力臂较大,也能使倒T型架产生明显的转动效果.
(2) 放大光斑在刻度尺上移动的距离
为了便于测量倒T型架转动的角度,卡文迪许在架上安装了平面镜M,M与支架同步旋转.倒T型架在一对力偶F作用下将会发生旋转,带动了悬丝的扭转.若悬丝被扭转的角度为θ,一束从光源照射到平面镜上的反射光则将转动角度2θ.由于θ较小,为了减小测量误差,卡文迪许在装置中增大了平面镜M到刻度尺的距离l.这样,虽然转动角度θ很小,光斑在刻度尺上移动距离x却可以较大,减小了测量中的相对误差.
2.2 比值法
卡文迪许扭秤实验的目的是“称”出地球质量M,算出地球密度ρ.那么,即使测出大铅球M1、小铅球m1之间的引力F,又怎样“称”出地球质量M?
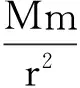
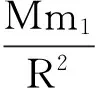
2.3 化归法
从物理学史来看,卡文迪许的实验目的是为了解决地球密度ρ的测量问题.在测量过程中,卡文迪许进行了多次化归,经过一次次转化和归结后得出地球密度ρ.
(1) 将地球密度的测量转化为地球质量的测量

(2) 将地球质量的测量转化为大、小铅球间的引力测量
具体思路在前面“比值法”中已经详述.
(3) 将大、小铅球间的引力测量转化为悬丝扭转角度的测量

(4) 将悬丝扭转角度的测量转化为光斑在刻度尺上移动距离的测量

可见,卡文迪许的每一步测量工作都放射出智慧的光芒,是物理思维方法的运用典范.

图3
18世纪,天文学得到迅速发展,物理学家们热衷于天体研究,如天体的运行半径、运行周期、天体的密度等,其中天体密度的测量一直没有能够实现.所以,当卡文迪许测出地球密度后,引起了轰动.英国物理学家J.H.坡印廷说:“卡文迪许扭秤实验开创了弱力测量新时代”.
3 波依斯运用缩小法对实验的改进
在卡文迪许间接测出引力常量之后,物理学家们依然致力于引力常量G的测定.1889年英国物理学家波依斯在研究卡文迪许扭秤实验时,受到用实验水槽对船进行模拟实验的启发,顿生灵感:要提高扭秤实验的精确度,与其按比例放大实验装置的尺寸,还不如按比例缩小.于是,波依斯按照缩小的思路对实验进行改进.卡文迪许扭秤装置的扭臂长度为6英尺,波依斯将其改为5/8英寸.波依斯认为,这样不但可以减少温度梯度、气流干扰等因素的影响,而且可以加大外部吸引物的作用效果.卡文迪许使用的铅锤直径为8英寸,而波依斯只用了直径为4.25英寸的吸引球,就相当于在卡文迪许的装置上用直径为27英尺的吸引球所产生的效果.再配合其他的一些改进,波依斯测得G=6.6578×10-11N·m2/kg2,其扭秤装置使得测量引力常量的精确度推进了两个数量级.
卡文迪许用放大法取得了实验测量的成功,而波依斯用缩小法大大提高了实验精度,思维方法真迷人.
[1] 郭奕玲,沈慧君.著名经典物理实验[M].北京:北京科技出版社,1991:43-48.
[2] 中学物理教师手册编写组:中学物理教师手册[M].上海:上海教育出版社,1982:88-91.
① 本文系江苏省教研室第十期立项课题“从物理规律的溯源出发培养学生物理思维方法的研究”(编号:L018)的阶段性成果.
名师简介:陈连余(1963— ),男,江苏省物理特级教师,人民教育出版社“新课程培训专家”,主要研究高中物理教学和高中物理竞赛.

