考虑尺度间相关性的电缆瓷套终端红外图像去噪*
牛海清 吴炬卓 许佳 吴倩 高紫建 郑文坚
(1.华南理工大学 电力学院, 广东 广州 510640; 2.珠海供电局, 广东 珠海 519000;3.广州供电局有限公司, 广东 广州 510620)
考虑尺度间相关性的电缆瓷套终端红外图像去噪*
牛海清1吴炬卓2许佳1吴倩3高紫建2郑文坚1
(1.华南理工大学 电力学院, 广东 广州 510640; 2.珠海供电局, 广东 珠海 519000;3.广州供电局有限公司, 广东 广州 510620)
为有效抑制图像噪声,提高电气设备红外诊断的准确性,采用基于小波系数尺度间相关性和双变量收缩函数的方法对电缆瓷套终端红外图像进行去噪.将图像进行小波分解,计算小波系数尺度间的相关系数,使用模糊c-均值聚类法对相关系数聚类,即将小波系数分为有效系数和无效系数两类.对无效小波系数直接进行置零处理,对有效小波系数使用双变量收缩函数进行处理,得到真实图像小波系数的估计值.最后,对处理得到的真实图像小波系数的估计值进行重构,便得到去噪后图像.含噪图像的去噪结果表明,运用文中方法能有效地去除红外图像中的噪声,且与使用传统软阈值方法去噪得到的图像对比,文中方法去噪后的图像信噪比更高,最小均方误差更小.
图像去噪;尺度间相关性;小波变换;相关系数;模糊c-均值;双变量收缩
红外热成像能够实现非接触性测量,具有不容易被电磁干扰、准确、安全等特点[1],近年来已广泛应用于电缆瓷套终端状态检测与故障诊断.红外热成像仪接收电缆瓷套终端的热辐射信号,并将其转换成相应的电信号,再经过信号处理后,被测电缆瓷套终端的表面热分布以人眼可见的图像呈现出来.当电缆终端存在某些缺陷时(如瓷套式终端进水),电缆终端瓷套表面温度分布有所变化.因此,可以通过分析红外图像来发现电缆瓷套终端的某些缺陷,从而减少事故的发生.
红外图像在生成过程中由于受周围环境噪声和仪器本身噪声影响而具有高噪声、低对比度的特点[2].因此,为了准确地对电缆瓷套终端进行缺陷及故障诊断,有必要对其红外图像进行去噪处理.
在图像去噪的研究中,比较常用的方法有自适应加权均值滤波、形态学去噪、模糊去噪、小波去噪[3-6]等.其中小波变换由于其良好的时频局部化能力,具有较好的去噪效果[7-8].在小波去噪方法中,基于小波系数阈值的滤波方法由于实现简单、重构信号误差小而得到广泛应用.Donoho在文献[9]中提出了软阈值收缩函数,该函数通过将小波系数和选定阈值比较进行收缩,其去噪效果和阈值选取密切相关.常用的阈值选取规则有VisuShrink阈值法[10]、SureShrink阈值法[11]、BayesShrink阈值法[12].软阈值收缩函数简单有效,但该函数实质是在对小波系数进行单变量Laplase分布建模时得到的,忽略了小波系数尺度间相关性.文献[13]中提出了一种基于小波系数统计数据和隐式马尔可夫模型的信号处理方法,该方法考虑了小波系数尺度间相关性,采用多个状态的混合高斯模型来描绘小波系数的分布,并取得了比传统软阈值方法更好的去噪效果.文献[14-16]中提出了一种基于双变量收缩函数的图像去噪方法,该方法采用非高斯的双变量分布模型来描述小波系数的分布,基于贝叶斯估计理论得到相应的非线性阈值函数,并取得了比传统软阈值方法和文献[13]中提出的隐式马尔可夫树法(HMT)更好的去噪效果.
文中在文献[14-16]已有研究的基础上,结合小波系数尺度间相关性,将电缆瓷套终端红外图像进行小波分解,定义和计算小波系数尺度间相关系数,并使用模糊c-均值法对相关系数进行聚类,即将小波系数划分成有效小波系数和无效小波系数两类,对无效小波系数进行置零处理,对有效小波系数采用双变量收缩函数进行处理,对处理后的小波系数进行二维小波反变换即可达到去除红外图像噪声的目的.
1 含噪图像信号小波系数的模糊分类
含噪图像信号经过二维小波变换后得到各分解尺度不同方向上的小波系数和最高分解尺度上的尺度系数.其中,有用图像信号所对应的小波系数幅值大、数量少,噪声所对应的小波系数幅值小、数量多.而尺度系数则主要集中了有用图像信号的能量.文献[17]中指出,经过小波变换之后,信号所对应的小波系数在各尺度上具有比较强的相关性,而噪声信号所对应的小波系数在尺度间缺乏这种明显的相关性.因而文中利用各尺度上小波系数的尺度间相关性来对小波系数进行分类.根据信号处理需要可以将小波系数划分为两类:有效系数和无效系数,前者对应于信号,后者对应于噪声.具体实现如下.
1.1 信号小波系数相邻尺度的相关系数
(1)
式中:kd=H,V,D,分别表示水平、垂直和对角线方向;l为参与相关计算的尺度数.随着分解尺度的增大,信号突变部分的宽度也会增大,而且在粗尺度上相邻的突变点会相互影响[18],因此文中取l=2,即式(1)可表示为
(2)
1.2 含噪图像信号小波系数的模糊c-均值分类
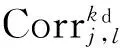
模糊c-均值聚类是一种基于划分的聚类算法,是普通c均值算法的改进,其实质上就是求解使得目标函数J最小时的隶属度矩阵[uij]D×N,以及类别中心V.
(3)
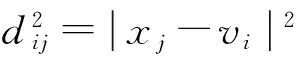
步骤1 根据式(3),首先确定聚类数目D,然后初始化聚类中心V及加权指数m;
步骤2 对第t次迭代,需要更新隶属度和D个聚类中心,其计算公式分别为
(4)
(5)
若目标函数J连续两次迭代的误差满足|J(t)-J(t-1)|≤ε,则迭代过程停止;若目标函数的误差不满足精度,则返回步骤2继续迭代.
迭代过程结束后,得到各数据对不同聚类中心的隶属度矩阵U=[uij]D×N.在决定数据点分类时,文中采用最大隶属度原则[19],则如果数据隶属于某聚类中心的程度最大,其就隶属于该聚类中心代表的类别.最大隶属度原则表示为
Ai0(u0)=max{A1(u0),A2(u0),…,AD(u0)}
(6)
则认为数据点u0相应隶属于类别Ai0.
文中将相关系数划分为两类,经聚类后阈值由下式决定:
(7)
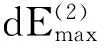
2 双变量收缩和局部方差估计
2.1 单变量收缩函数
y=w+n
(8)
式中,y为含噪图像的小波变换系数,w为原始图像的小波变换系数,n为噪声的小波变换系数.
则原始图像的小波变换系数的最大后验估计(MAP)为
(9)
式中,pw|y为条件概率密度函数,应用贝叶斯定律,由式(9)可得
(10)
式中,pn表示噪声的概率密度函数,pw表示原始图像小波系数的概率密度函数.其中,pn为零均值的高斯白噪声分布,即
(11)
式(10)可以变换为
(12)
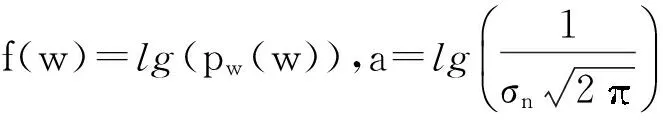
(13)
式(13)相当于解方程
(14)
在图像去噪方面,有许多统计模型被用来描述小波系数的分布,其中拉普拉斯模型应用比较广泛[20].拉普拉斯模型的数学表达式只有标准差σ一个参数,结合MAP估计和贝叶斯定律通常可以得到解析解.因此,文中对尺度内小波系数的分布特性进行拉普拉斯建模,即
(15)
那么式(14)的解为
(16)
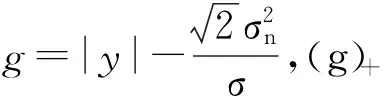
(17)
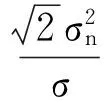
2.2 双变量收缩函数
和一维小波变换的小波系数一样,二维小波变换的小波系数在纵向上具有传播性,即不同尺度间同一位置上的小波系数幅值之间存在传播性,为考虑图像小波系数的这一分布特性,需要对小波系数的分布模型作如下修改:
(18)
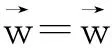
(19)
即得出w1的MAP估计为
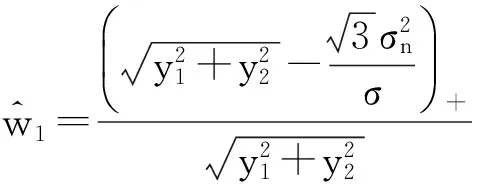
(20)
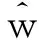
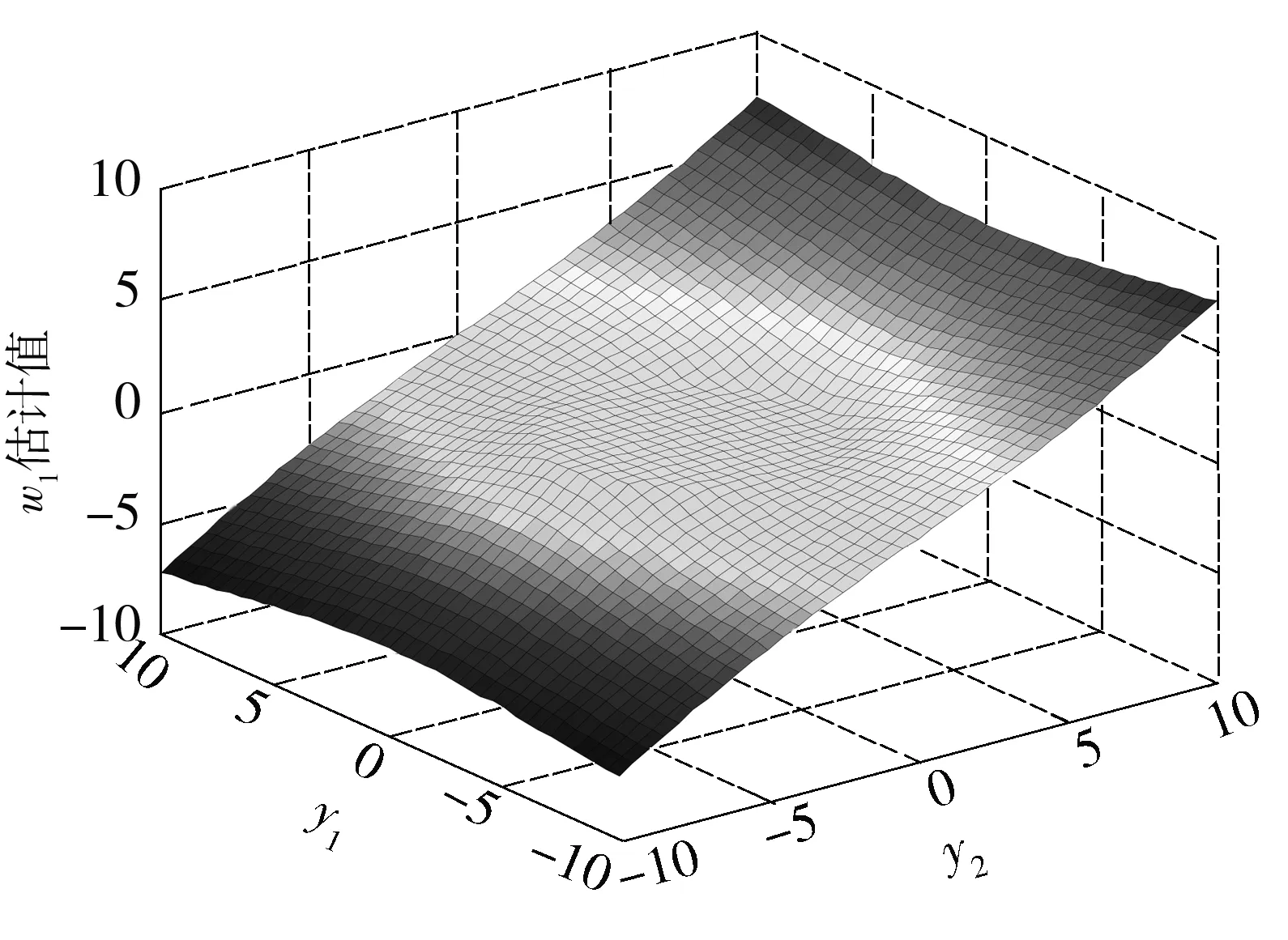
图1 双参数收缩函数图
2.3 局部方差估计
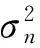
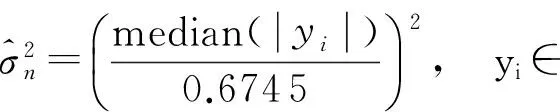
(21)
式中,HH为对角线方向.
(22)
式中,M为矩形窗区域N(k)的大小.由此得到σ的估计为
(23)
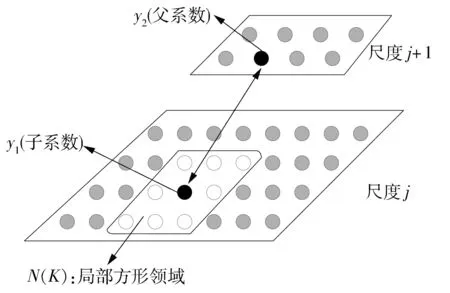
图3 领域N(k)示意图
3 电缆瓷套终端红外检测图像去噪
3.1 电缆瓷套终端红外检测
为提高电缆线路的供电可靠性和稳定性,广州供电局每个季度对所有电缆线路的瓷套终端进行红外检测.当瓷套终端存在发热缺陷时,会在其对应的红外图像里面反映出来,通过分析红外图像的特征,就可以判断出终端发热的位置和类型.图4为对某瓷套终端进行红外检测得到的红外图像.

图4 红外图像
从图4可以看出,瓷套终端的应力锥部位存在明显的局部发热现象,其中发热区域的最高温度达到27.1 ℃,而瓷套终端底部最高温度为25.0 ℃,两者相差为2.1 ℃,远远超过了正常范围,说明瓷套终端存在发热缺陷,需要查找和排除.
通过对该终端的缺陷查找发现,该终端由于密封不好存在进水现象,其内部进水水位已经达到应力锥的顶部.当终端内部进水时,由于水的密度比里面填充硅油的密度大,所以水分会集中在终端下部,使接近水的那部分硅油的介质损耗角正切变大.由介质损耗功率公式P=U2ωCtanδ(U为施加电压,ω为施加电压角频率,C为介质等效电容,δ为介质损耗角)可知,硅油的介质损耗功率与其介质损耗角正切和施加电压平方成正比.由于瓷套终端应力锥部分的电压分布比较集中,故该区域的发热比终端其他部位明显.此外,由于终端进水,可能导致泄露电流增大,进而使发热量增加.3.2 去噪算法
依据上述原理,基于双变量收缩函数和局部方差估计去噪算法的具体步骤如下:
步骤1 将红外图像信号进行二维小波分解,得到最高分解尺度上的尺度系数和各分解尺度不同方向上的小波系数.
步骤2 用式(2)计算每个小波系数的相关系数.
步骤3 使用模糊c-均值聚类法将小波系数分为有效小波系数和无效小波系数两类.
步骤4 将每一个无效小波系数置零.对每一个有效小波系数进行如下处理:
步骤5 对最高分解尺度上尺度系数和由(4)得到的小波系数估计值进行二维小波重构,就可以得到去噪后的红外图像信号.
3.3 电缆瓷套终端红外图像去噪的仿真
为方便对图像进行处理,笔者在对红外图像进行去噪处理之前先对图像进行预处理,即将红外图像的真彩图转换为灰度图.将如图4所示的电缆瓷套式终端红外图像(大小为240像素×240像素)转换为对应的灰度图,加入不同噪声水平(噪声标准方差分别为5、10、15、20)的高斯白噪声,即可得到不同信噪比的含噪图像.如图5所示是标准方差为15的含噪图像.
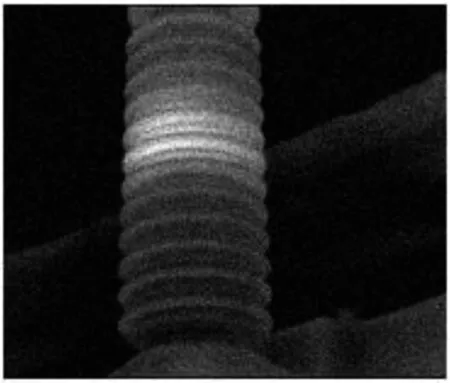
图5 含噪图像
文中采用前述基于小波系数尺度间相关性和双变量收缩函数的自适应去噪方法,对不同高斯噪声水平的含噪电缆瓷套终端红外图像进行去噪.试验中采用sym4小波对图像进行小波分解,分解层数为3,矩形窗区域N(k)的大小取为3×3.
此外,作为与试验的对比,分别采用Rigrsure规则阈值法、Sqtwolog规则法、Minimaxi规则阈值法,并结合软阈值函数对红外图像进行去噪.
文中采用文献[21]中定义的最小均方误差MSE和信噪比SNR作为评估去噪效果好坏的指标,MSE越小,SNR越大,去噪效果越好.
(24)
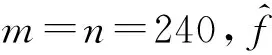
(25)
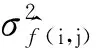
3.4 结果与分析
表1给出了采用不同去噪算法去噪后图像质量评价参数的计算结果.从表1可以看出,在噪声方差相同的情况下,与Rigrsure阈值法、Minimaxi阈值法以及Sqtwolog阈值法相比,利用文中方法对图像进行去噪后信噪比更大,最小均方误差更小,说明文中方法的去噪性能要比上述3种阈值方法更好.当噪声水平高时,采用文中方法去噪后图像的信噪比和最小均方误差较3种阈值法有明显的提高,说明本方法适用于信噪比小、噪声水平高的红外图像去噪.
表1 文中方法和传统阈值法对不同噪声水平的含噪红外图像去噪后的评价参数
Table 1 Evaluating parameters of denoising noisy image contaminated by various noises using the proposed method and traditional threshold methods
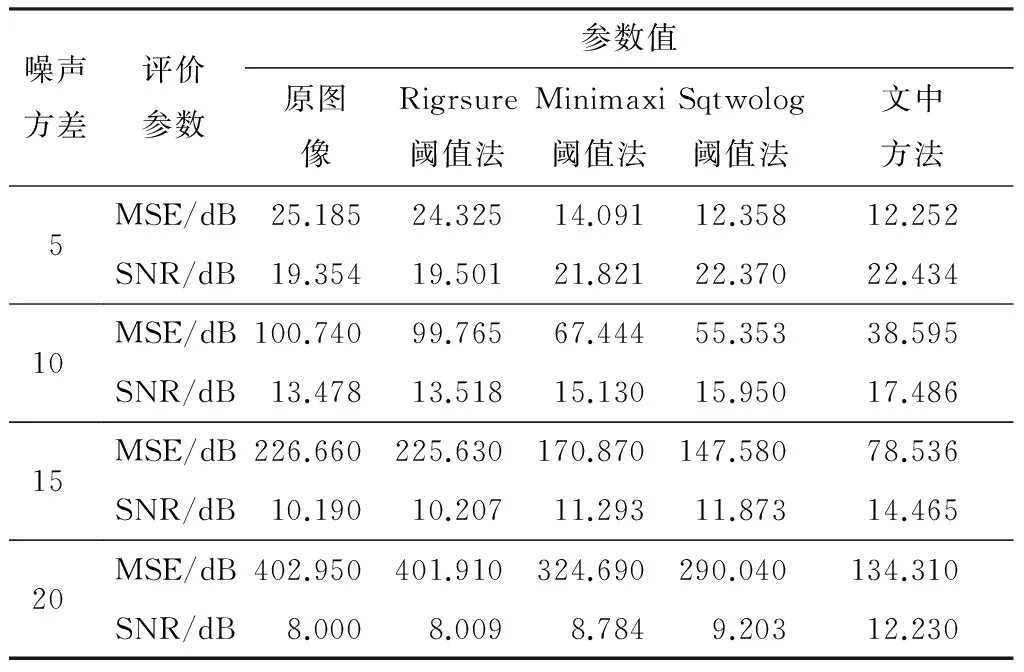
噪声方差评价参数参数值原图像Rigrsure阈值法Minimaxi阈值法Sqtwolog阈值法文中方法5101520MSE/dB25.18524.32514.09112.35812.252SNR/dB19.35419.50121.82122.37022.434MSE/dB100.74099.76567.44455.35338.595SNR/dB13.47813.51815.13015.95017.486MSE/dB226.660225.630170.870147.58078.536SNR/dB10.19010.20711.29311.87314.465MSE/dB402.950401.910324.690290.040134.310SNR/dB8.0008.0098.7849.20312.230
图6的4个小图分别是采用Rigrsure阈值法、Minimaxi阈值法、Sqtwolog阈值法、文中方法去噪后的图像.对比发现,在保持完整图像细节的情况下,文中提出的方法去噪后的图像更加清晰,具有更好的去噪效果.




图6 不同去噪方法去噪后图像
Fig.6 Denoised images obtained by different denoising methods
4 结论
文中针对电缆瓷套终端红外图像去噪和小波系数尺度间存在相关性问题,提出了一种基于小波系数尺度间相关性和双变量收缩函数的局域自适应去噪方法.该方法的特点是:
(1)定义小波系数的尺度间相关系数,将相关系数的大小模糊化,使用模糊c-均值阈值法将相关系数划分为两类.对相关系数绝对值小于阈值的小波系数进行置零处理,对相关系数绝对值大于阈值的小波系数进行收缩处理.
(2)考虑小波系数尺度间相关性,引入双变量概率分布模型描述小波系数,进而由MAP估计和贝叶斯定律得到双变量收缩函数;再基于层内局域方差估计得到每个有效小波系数的估计值,对估计小波系数进行重构即可得到去噪后的图像.
文中分别采用3种阈值法和文中提出的基于小波系数尺度间相关性和双变量收缩函数去噪方法,对含有不同噪声水平的电缆瓷套终端红外图像进行仿真去噪处理,并使用信噪比和最小均方误差对去噪效果进行评价.对比不同去噪算法去噪后的图像和评价参数可以得出以下结论:文中提出的去噪方法能够在有效去除噪声的同时,完整保留图像信息;文中方法去噪后图像的信噪比更高,最小均方误差更小,具有更好的去噪效果,尤其是在强噪声下,去噪效果更佳.
[1] 何洪英,姚建刚,蒋正龙,等.利用红外图像特征和径向基概率神经网络识别不同湿度条件下绝缘子的污秽等级 [J].中国电机工程学报,2006,26(8):117-123. HE Hong-ying,YAO Jian-gang,JIANG Zheng-long,et al.Contamination grades recognition of insulators under different humidity using infrared image features and RBPNN [J].Proceedings of the CSEE,2006,26(8):117-123.
[2] 田裕鹏.红外检测与诊断技术 [M].北京:化学工业出版社,2006:200-217.
[3] MALLAT S,HWANG W L.Singularity detection and processing with wavelets [J].IEEE Transactions on Information Theory,1992,38(2):617-643.
[4] 左问,张毅刚,郁惟镛,等.基于小波域隐式马尔科夫模型的发电机局部放电信号去噪 [J].中国电机工程学报,2003,23(6):137-142. ZUO Wen,ZHANG Yi-gang,YU Wei-yong,et al.Wavelet-based partial discharge denoising using hidden markov model [J].Proceedings of the CSEE,2003,23(6):137-142.
[5] 杨恢先,王绪四,谢鹏鹤,等.改进阈值与尺度间相关的小波红外图像去噪 [J].自动化学报,2011,37(10):1167-1173. YANG Hui-xian,WANG Xu-si,XIE Peng-he,et al.Infrared image denoising based on improved threshold and inter-scale correlations of wavelet transform [J]Acta Automatica Sinica,2011,37(10):1167-1173.
[6] 姜三平.基于小波变换的图像降噪 [M].北京:国防工业出版社,2008.
[7] DONOHO D L,JOHNSTONE I M.Adapting to unknown smoothness via wavelet shrinkage [J].Journal of the American Statistic Association,1995,90(432):1200-1224.
[8] RABINER L R.A tutorial on hidden markov models and selected applications in speech recognition [C]∥Proceedings of the IEEE.[S.l.]:IEEE,1989.[9] DONOHO D L.De-noising by soft-thresholding [J].IEEE Transactions on Information Theory,1995,41(3):613-627.[10] DONOHO D L,JOHNSTONE I M.Ideal spatial adaptation by wavelet shrinkage [J].Biometrika,1994,81(3):425-455.
[11] CHESNEAU,CHRISTOPHE,LECUE Guillaume.Adapting to unknown smoothness by aggregation of thre-sholded wavelet estimators [J].Statistica Sinica,2009,19(4):1407-1411.
[12] CHANG S,YU B,VETTERLI M.Adaptive wavelet thresholding for image denoising and compression [J].IEEE Transactions on Image Processing,2000(9):1532-1546.
[13] CROUSE M S,NOWAK R D,BARANIUK R G.Wavelet-based statistical signal processing using hidden markov models [J].IEEE Transactions on Signal Processing,1998,46(4):886-902.
[14] LEVENT S,SELESNICK I W.Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency [J].IEEE Transactions on Signal Proces-sing,2002,50(11):2744-2756.
[15] LEVENT S,SELESNICK I W.Multivariate shrinkage functions for wavelet-based denoising [J].IEEE Transactions on Signal Processing,2002:953-957.
[16] LEVENT S,SELESNICK I W.Bivariate shrinkage with local variance estimation [J].IEEE Signal Processing Letters,2002,9(12):438-441.
[17] 李仲宁,罗志增.基于小波变换的空域相关法在肌电信号中的应用 [J].电子学报,2007,35(7):1413-1418. LI Zhong-ning,LUO Zhi-zeng.Spatial correlation filtering based on wavelet transformation application to EMG de-noising [J].Acta Electronica Sinica,2007,35(7):1413-1418.
[18] 张志刚,周晓军,杨富春,等.基于小波系数相关性和局部拉普拉斯模型降噪方法 [J].振动与冲击,2008,27(11):32-36. ZHANG Zhi-gang,ZHOU Xiao-jun,YANG Fu-chun,et al.Denoising method based on wavelet transform coefficient correlation and local laplacian model [J].Journal of Vibration and Shock,2008,27(11):32-36.
[19] 杨纶标,高英仪.模糊数学原理及应用 [M].广州:华南理工大学出版社,2005.
[20] 易翔,王蔚然.基于小波域统计混合模型的图像降噪方法 [J].电子与信息学报,2005,27(11):1722-1725. YI Xiang,WANG Wei-ran.Method of image denoising based on statistieal mixture model in wavelet domain [J].Journal of Electronics & Information Technology,2005,27(11):1722-1725.
[21] FODOR I K,KAMATH C.Denoising through wavelet shrinkage:an empirical study [J].Journal of Electronic Imaging,2003,12(1):151-160.
Denoising of Infrared Images of Porcelain Sleeve Cable Terminal Considering Inter-Scale Correlation
NIUHai-qing1WUJu-zhuo2XUJia1WUQian3GAOZi-jian2ZHENGWen-jian1
(1.School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China;2.Zhuhai Power Supply Bureau, Zhuhai 519000, Guangdong, China;3.Guangzhou Power Supply Bureau, Guangzhou 510620, Guangdong, China)
In order to effectively suppress the noise of images and improve the accuracy of infrared diagnosis of electrical equipment, a denoising method based on both the wavelet coefficients’ inter-scale correlation and the bivariate shrinkage function is proposed to denoise the infrared images of porcelain sleeve cable terminals. In this method, first, the wavelet transform coefficients are separated into two sorts by means of fuzzyc-means clustering according to the calculated inter-scale correlation coefficients of wavelet coefficients, namely, the efficient coefficients and the invalid coefficients. Then, the invalid wavelet coefficients are directly set to zero, while the efficient wavelet coefficients are processed with the bivariate shrinkage function. Thus, the estimated values of image’s wavelet coefficients are obtained. Finally, the estimated wavelet coefficients are used to reconstruct a denoised image. The denoising results of infrared images with noise show that, as compared with the traditional soft thresholding method, the proposed method is more effective because it improves both the signal-to-noise ratio and the mean square error.
image denoising; inter-scale correlation; wavelet transform; correlation coefficient; fuzzyc-means; bivariate shrinkage
2016-06-07
国家高技术研究发展计划(863计划)项目(2015AA050201) Foundation item: Supported by the National High-Tech R&D Program of China(863 Program)(2015AA050201)
牛海清(1969-),女,博士,副教授,主要从事高压电缆线路及高压电气设备研究.E-mail:niuhq@scut.edu.cn
1000-565X(2017)04-0015-07
TM 726
10.3969/j.issn.1000-565X.2017.04.003

